基于滑移边界法的微型涡喷发动机用高速发电机优化设计

，

(南京航空航天大学自动化学院，江苏 南京 211106)

0 引言

电机优化设计采用的方法有多目标分解随机粒子群优化算法[1]，多目标遗传优化方法[2]，多目标的混合全局优化算法[3]等。可用参数化网格剖分法简化算法机制[4]，通过梯度算法提高优化效率[5-6]。

传统有限元仿真需要反复重构转子不同位置时对应的模型进行反电势和电感计算[7-9]，电机优化设计复杂。为简化电磁参数计算过程，提出基于滑移边界条件的电机有限元模型，并将基于该模型的电磁参数计算与梯度下降法相结合，提出的改进梯度下降优化设计能提高优化效率。

1 高速发电机设计流程

发电机的电磁设计包括反电动势、电感、损耗、温升等参数的计算。对于损耗和温升的核算方法始终是高速发电机设计中的热点问题。这里需要明确的是，尽管微型涡喷发动机用发电机在高转速下产生了量值极大的损耗密度，但这对发电机的正常运行影响甚微，这是因为微型涡喷发动机在高转速下所需的高速来流对发电机起到了很好的散热效果，作者已在参考文献[10]中对高速发电机的损耗、温升的计算方法进行过研究，并在多台微发系统实际的运行实践中证明发电机不论是空载还是满载，在很宽的工作转速内其长时间运行的温度始终只略高于环境温度。因此对于微型涡喷发动机用发电机的体积优化，只需以反映电机发电性能的电动势和电感参数作为状态变量。故而，微型涡喷发动机用发电机的设计流程如图1所示。

图1 高速永磁发电机设计流程

2 高速发电机滑移边界有限元模型

2.1 滑移边界条件

在求解不同转速下定子铁心磁场的时域解时，传统的有限元方法需要反复重构转子不同位置时候对应的模型来进行磁场分析。这就使得每次重构后的有限元模型中单元、节点信息发生变化，加大了定子铁心损耗仿真计算的难度，降低了仿真效率。所以，将滑移边界法融入到高速永磁发电机二维有限元模型中去，无需重构模型，保证了计算的精准性，降低了仿真难度[10]。

滑移边界即将整个电机模型从气隙中心线割成两个独立的部分进行建模、划分网格，定子部分的内边界与转子部分的外边界在分割线位置重合、但不共线。在图2和图3中，模型中间的虚线为滑移边界耦合线。模型建好后，定、转子模型就固定不动，通过滑移边界线上的节点磁位的耦合来等效定、转子间的位置变化。若转子的角速度为v, 滑移边界线上的节点为360个(定子、转子边界线各360个节点)，在t= 0时刻，通过将(r0,s0)，(r1,s1) ，…，(r359,s359) 对应节点的磁位进行耦合可得转子初始位置的磁场分布，如图2所示。在t=45°/v时刻将(r45,s0)，(r46,s1)， …，(r89,s44)，(r90,s45)， …，(r44,s359)对应节点的磁位进行耦合即可得到转子旋转45°位置的磁场分布，如图3所示。以此类推得到转子旋转一周在电机中各位置产生的磁场波形。

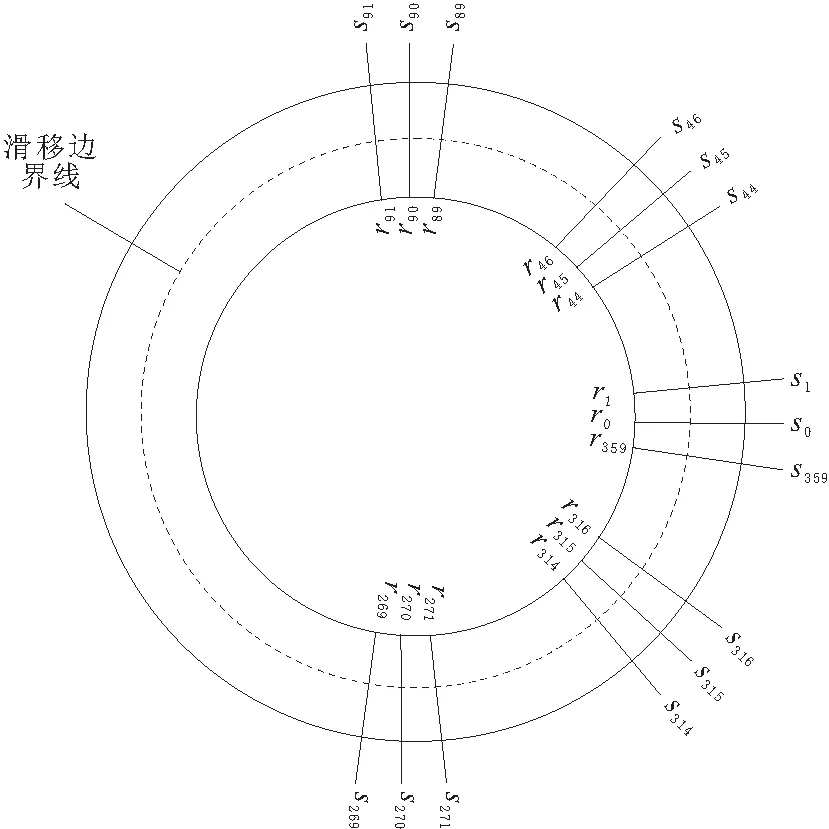
图2 t=0时滑移边界线上的节点耦合

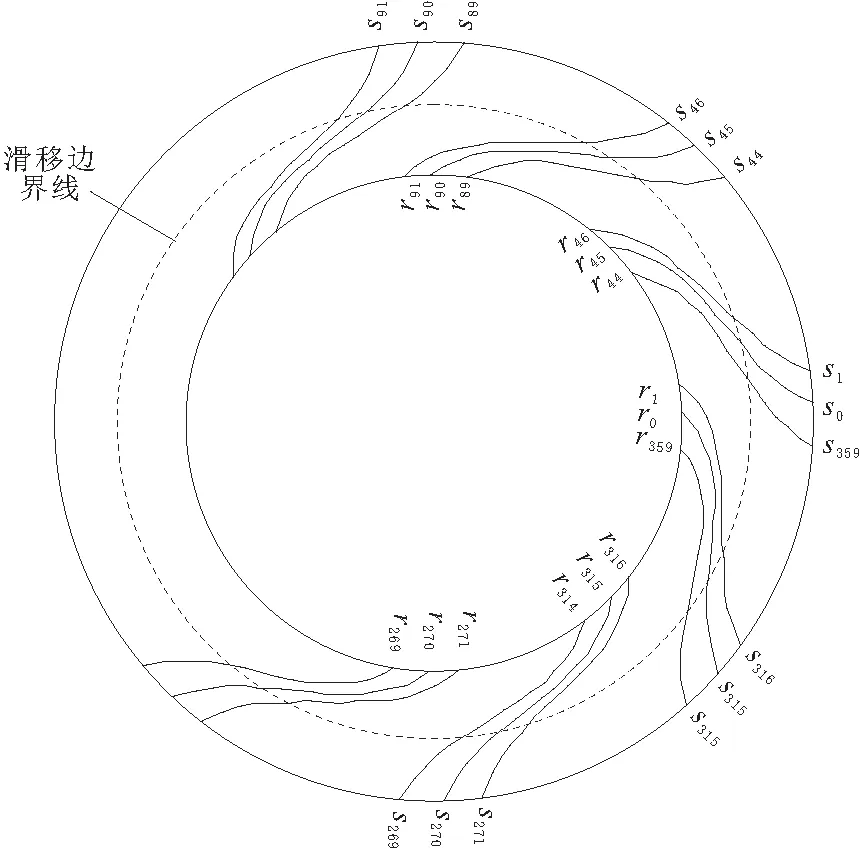
图3 t=45°/v时滑移边界线上的节点耦合

2.2 发电机结构形式及滑移边界有限元模型

微型涡喷发动机对高速发电机的机械性能要求较高，这就要求发电机在拓扑结构上要尽量简单，并且还要具备高功率密度。永磁发电机是较好的方案[11]。由于微型涡喷发动机对高速发电机有极好的冷却效果，运行过程中由电磁原因引起永磁退磁的可能性很小。结合滑移边界条件，以图4的高速发电机拓扑结构为例开展发电机电磁参数计算及优化设计的研究。

图4 微型涡喷发动机用高速发电机拓扑结构

3 电磁参数计算

3.1 空载反电势

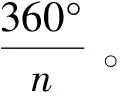
通过有限元仿真计算，可以得到A相绕组的磁位：

(1)

(2)

Ae是A相绕组中每个单元的磁位；Ve是每个单元的面积；ΩA1,ΩA2,ΩA3,ΩA4是磁通穿入A相绕组的区间；Ωx1,Ωx2,Ωx3,Ωx4是磁通穿出A相绕组的区间。进出A相绕组的磁位差即为A相绕组的磁通，可通过下式计算得到：

φA=AinA-AoutA

(3)

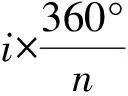
(4)

C为电机槽数；m为电机绕组相数；l为铁心轴向长度。

A相绕组各点的反电势可通过磁链对时间求导得到，即：

(5)

同理，可求的电机绕组B相，C相绕组各点的反电势，uB(i) ，uC(i)。

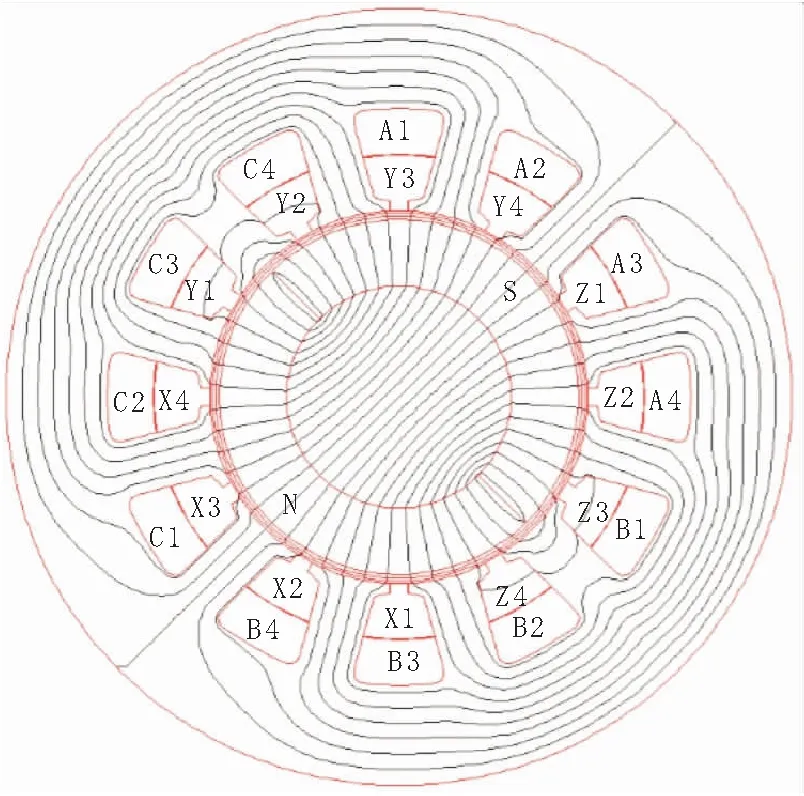
图5 发电机θ=0°空载磁场分布

图6 发电机网格剖分图

3.2 线圈电感

高速电机定子绕组阻抗的大小决定了电机的带载能力，输出负载电流通过电机绕组阻抗时，会在电机绕组上产生降落的电压降，导致输出电压降低。因此在高速电机优化设计过程中，电机定子绕组电感的计算是至关重要的一部分。

采用能量增量法来进行电感求解，即通过扰动电流引起的系统磁场能量的增量来计算，不需要计算系统的绝对磁场能量,仅需要计算能量增量，适用于非线性问题[8-9]。利用有限元分析获得高速电机磁场分布之后,分别计算通入电流(Ie+ΔIe)时的能量W(Ie+ΔIe)和通入电流(Ie-ΔIe)时的能量W(Ie-ΔIe)[12-13]。则在电流为Ie时的电感L就可以通过下式获得：

(6)

ΔIe为电流增量。

4 发电机优化设计方法

4.1 改进梯度下降优化算法

梯度下降法是一种物理意义清晰，运算法则简单的数值计算方法，其核心是以梯度法为基础来求解多维无约束最优化问题。任意一点的负梯度方向是函数值在该点下降最快的方向，那么利用负梯度作为极值搜索方向可以达到搜索区间最速下降的目的。而由极值点导数性质可知该点梯度为0，所以终止条件就是梯度逼近0，即搜索区间逼近极值点。

将基于滑移边界有限元模型的电磁参数计算法与梯度下降优化方法相结合，并对高速发电机进行优化设计。以电机的额定负载时的输出电压Ue和槽满率F作为设计指标，通过改变电机的永磁体厚hp；轴向长度L；定子外径D和绕组匝数N，实现发电机的最小尺度优化。

定义设计变量为：

X=[hp,D,L,N]

(7)

设计变量X服从下列约束：

(8)

且设计指标要满足下列约束:

(9)

(10)

a是并联导线数；r为导体半径；Ac为单个定子槽的面积。

电感上的电压降为：

ΔUe=2πfLI

(11)

额定负载下电机的输出相电压Ue可以表示为：

Ue=Uo-ΔUe

(12)

f为电机频率；L为电机平均电感；I为额定电流；Uo为电机空载基波电压。

定义目标函数为：

(13)

目标函数的梯度为：

(14)

每个设计变量的梯度也可近似表示为：

(15)

向量e的第i个元素为1，其他元素为0。

(16)

ΔD为指前向差分步长。

改进梯度下降优化方法具体流程如图7所示。

图7 改进梯度下降法流程

4.2 优化结果分析

以一个800 W的高速发电机为例，其主要技术指标如表1所示。基于改进梯度下降法对电机进行优化分析后，得到下列几组符合条件的优化结果。本次电机优化的目标是让电机在满足各项性能指标的情况下实现体积的最小化，由表2可知，第9组数据最优，满足技术指标和约束条件。

表1 电机技术指标

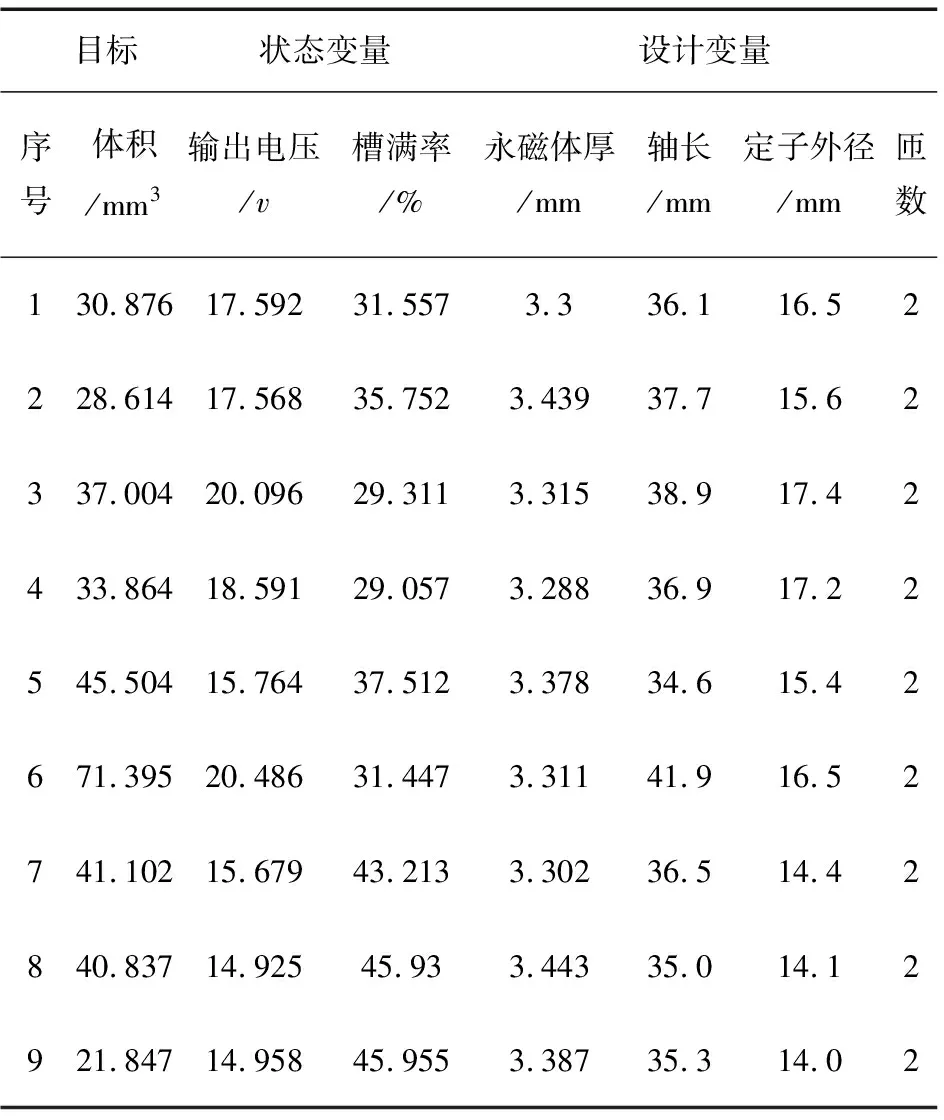
表2 电机的优化结果

5 实验验证

按照上述优化设计方法，设计优化了多种型号规格的微型涡喷发动机用发电机。图8为高速电机样机实物分解图，表3列出了这几台电机的实验测试结果和仿真结果的比较。其计算与测试结果很好的吻合，由于实际测试时是通过加载小电流来测线电感，而仿真时是加载额定电流来计算线电感，所以仿真结果比实际测试结果略小。

在此基础之上，对装配在微型涡喷发动机上的发电机进行了系统发电实验。图9为电机不同转速下的外特性测试结果波形。由实验结果可知，基于改进梯度下降法优化设计所得的微型涡喷发动机用高速发电机满足各项性能指标，从而验证了提出的优化设计方法的有效性和可行性。

图8 高速永磁电机样机实物分解

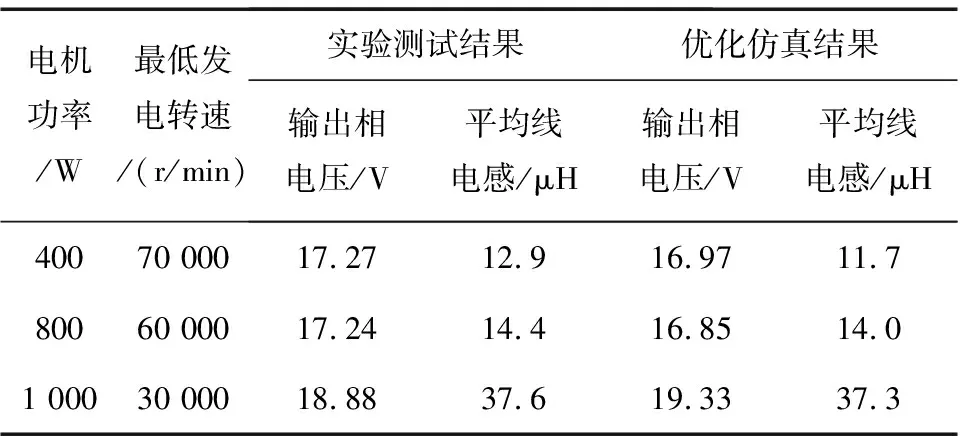
电机功率/W最低发电转速/(r/min)实验测试结果优化仿真结果输出相电压/V平均线电感/μH输出相电压/V平均线电感/μH40070 00017.2712.916.9711.780060 00017.2414.416.8514.01 00030 00018.8837.619.3337.3

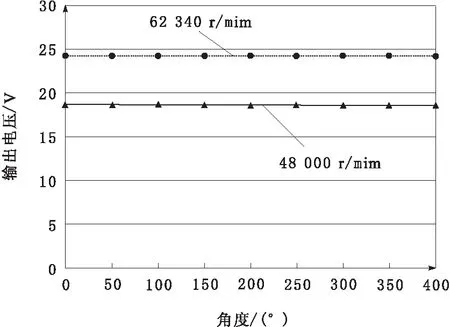
图9 高速发电机外特性实验波形

6 结束语

在传统的高速发电机有限元模型上改进，提出一种滑移边界有限元模型，解决了传统有限元建模分析需要反复重构转子不同位置时对应模型的问题。同时基于滑移边界有限元模型对高速发电机反电势和电感进行了仿真计算，这在一定程度上缩短了高速电机的设计周期，简化了设计过程，提高了工作效率。将滑移边界有限元模型应用到电磁计算中，并与梯度下降优化方法相结合，提出改进梯度下降优化算法，并对微型涡喷发动机用高速发电机进行优化设计，得到一系列满足高速发电机性能指标的设计参数，从中选取最优设计。最后，基于改进梯度下降优化方法设计了多台微型涡喷发动机用高速发电机样机，并通过对样机的反电势、电感等电磁参数测试验证了该优化方法的有效性，在微型涡喷发动机用高速发电机优化设计领域具有一定的通用性。

参考文献：

[1] 王光辉, 陈杰, 蔡涛,等. 多目标分解随机粒子群优化算法及其在直线电机优化设计中的应用[J]. 控制理论与应用, 2013, 30(6):693-701.

[2] VAEZ-ZADEH S, ISFAHANI A H. Multiobjective design optimization of air-core linear permanent-magnet synchronous motors for improved thrust and low magnet consumption[J]. IEEE Transactions on Magnetics, 2006, 42(3):446-452.

[3] 范坚坚, 吴建华, 沈磊,等. 极间隔断Halbach型磁钢的永磁同步电机多目标优化设计[J]. 电工技术学报, 2009, 24(9):53-58.

[4] 刘慧娟, 傅为农. 一种参数化网格剖分方法及其在电机优化设计中的应用[J]. 中国电机工程学报, 2012, 32(21):125-130.

[5] 曹先庆. 一种快速的永磁同步电动机效率优化方案[J]. 微电机, 2013, 46(10):69-73.

[6] 崔皆凡, 刘娜. 有限元结合并行梯度遗传算法及其应用[J]. 组合机床与自动化加工技术, 2012(5):17-20.

[7] 陈定积, 刘泉, 王先逵,等. 永磁同步直线电机空载反电势的分层有限元分析[J]. 清华大学学报(自然科学版), 2004, 44(2):212-214.

[8] 孙东森, 葛宝明, 毕大强,等. 高速开关磁阻电机的电感计算与运行分析[J]. 北京交通大学学报, 2010, 34(5):74-77.

[9] 王世山, 刘泽远, 邓智泉. 增强能量增量法求解无轴承开关磁阻电机电感[J]. 南京航空航天大学学报, 2009, 41(1):85-90.

[10] 吴云鹏. 高速永磁发电机电磁设计方法及关键技术研究[D]. 南京：南京航空航天大学, 2014.

[11] HUANG Y K, DONG J N, ZHU J G, et al. Core loss modeling for permanent-magnet motor based on flux variation locus and finite-element method [J]. IEEE Transactions on Magnetics, 2012, 48(2):1023-1026.

[12] NEHL T W, FOUAD F A, DEMERDASH N A. Determination of saturated values of rotating machinery incremental and apparent Inductances by an energy perturbation method[J]. IEEE Transactions on Power Apparatus & Systems, 1982, PAS-101(12):4441-4451

[13] 姚新祥, 黄贤蕾, 王周叶,等. 永磁同步电机电感参数的计算[J]. 家电科技, 2015(3):69-71.