基于CMAC的电动负载模拟器的研究

，

(南京航空航天大学航空宇航学院，江苏 南京 210016)

0 引言

电动负载模拟器是一种用于飞行器控制系统半实物仿真的关键设备[1]。它能够模拟飞行器舵面在飞行过程中所受到的气动载荷，用来验证飞行控制系统的参数，考核舵机系统的带载性能。电动负载模拟器具有自身噪音和环境污染小，可靠性高、易维护等优点，已广泛地应用于小载荷情况的加载领域[2]。

电动加载的关键问题就是如何消除系统中的多余力矩[3]，目前采取的策略主要有结构补偿法、经典控制补偿法[4-5]和神经网络控制法[6-7]。在此，将常规CMAC网络[8]和PID复合控制算法应用到电动负载模拟器的控制中，传统PID保证系统稳定性，CMAC实现前馈控制来提高系统的快速性和加载精度，针对常规CMAC网络存在的过学习现象，修正了权值调整算法。

1 电动负载模拟器的组成和数学模型

电动负载模拟器主要由加载电机、角度传感器、力矩传感器、主控计算机等组成，电动加载的系统结构如图1所示。图1的右侧为舵机系统，由舵机和角度传感器等构成，图1的左侧为加载系统，在加载过程中，舵机按照位置指令进行运动，实际的输出舵机角位移由编码器检出，力矩指令和力矩传感器的反馈力矩进行比较得到偏差信号，再经过控制器的运算产生精确的电压信号来控制加载电机输出力矩。

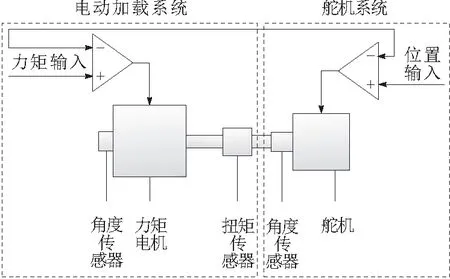
图1 电动负载模拟器系统结构

首先建立力矩电机的数学模型。其工作原理与直流电动机相同，根据机理法来建立电动机的数学模型。电压平衡方程为：

(1)

Ua为电枢两端电压；La为电枢电感；ia为电枢电流；Ra为电枢回路总电阻；E为电枢感应电动势。

E=Keω

(2)

Ke为电机反电动势系数；ω为电机转子转动的角速度。

直流力矩电机的力矩平衡方程为：

(3)

Te为电磁转矩；Jm为电动机转轴及负载折算到电动机输出轴的转动惯量；Bm为电动机粘性阻尼系数；Tl为作用到电机轴的负载转矩。

电磁转矩Te为：

Te=Ktia

(4)

Kt为电磁转矩系数。

然后建立扭矩传感器的数学模型。扭矩传感器用于测量系统中实际的转矩，其摩擦和惯量均比较小，故在测量范围内视其为比例环节。

Tl=Kt(θ1-θ2)

(5)

Kt为传感器的扭转刚度；θ1为加载电机转动的角度；θ2为舵机转动的角度。

最后建立驱动器数学模型。电机驱动器的工作带宽远大于系统带宽，在建立数学模型时，也将其视为比例环节。

U=KU

(6)

K为电机驱动器比例增益系数。

联立上述方程式得系统开环传递函数为：

(7)

A0=Jm1La1s3；A1=(BmLa+JmRa)s2；A2=(RaBm+LaKt+KeKt)s；A3=RaKt；B0=KtJmLas2；B1=Kt(BmLa+JmRa)s；B2=Kt(RaBm+KeKt)；B3=KtKtK。

由系统传递函数可知，加载系统输出力矩主要由2部分构成：一部分为控制输入项，由电枢电压Ua1来决定；另一部分为力矩干扰项，此部分由舵机运动的速度所带来的，即所谓的“多余力矩”，当舵机剧烈运动时会对加载系统带来强烈的干扰，必须采取措施抑制系统的多余力矩。

2 小脑模型神经网络

CMAC网络是一种能够表达复杂非线性函数的表格查询型自适应神经网络[9-10]。其基本思想是在输入空间给出一个状态，从存储单元中查找到对应的状态地址，然后将所有查询到的状态地址的内容进行求和求出CMAC的输出值，求出此输出响应值与期望值之间的误差，并利用学习算法来改变被激活的状态地址中存储的内容。其结构如图2所示。

图2 CMAC网络结构

CMAC神经网络的工作过程中主要包括输入空间的划分，输入层到输出层之间的非线性映射和输出层权值更新学习算法。其中网络结构中的映射主要包括概念映射和实际映射。

2.1 概念映射

概念映射是指将输入空间的向量u映射至概念存储器AC。

设n维输入空间的向量为：

up=[u1p,u1p,…,unp]T

(8)

量化编码表示为[up]，设概念存储器AC的存储单元个数为C，则采用下式将输入空间u向量映射至概念存储器AC的C个存储单元中：

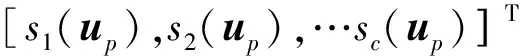
(9)

sj(up)=1,j=1,2,…,c

(10)

映射原理根据输入空间中邻近的2个点(1个点代表1个n维输入向量)会在概念存储器AC中有部分的重叠单元被激励，它们之间的距离越近则重叠单元越多，距离越远，重叠单元越少。这种映射关系就是局部泛化，其中c为泛化参数，泛化参数取值范围为0～100。

2.2 实际映射

实际映射是指将概念存储器AC的c单元映射到实际存储器AP的c个单元，采用的编码技术为杂散编码技术，实际存储器AP的c个单元中存储相应的权值，将所有的权值求和记得到CMAC网络的输出。

考虑只有单输入的情况下，网络输出为：

(11)

wk=[w1,w2,…,wc]T

(12)

将式(10)带入式(12)可以得到：

(13)

2.3 学习算法

CMAC利用δ学习规则进行调整权值大小，权值调整指标E为：

(14)

e(t)=r(t)-y(t)，即系统输入和网络输出之间的偏差

常规CMAC采用梯度下降法进行权值更新，更新公式为：

(15)

wj(t)=wj(t-1)+Δwj(t)+

α(wj(t-1)-wj(t-2))

(16)

η为学习率，一般取值为0<η<1；α为惯性系数。

常规CMAC网络因为需要多个学习过程才能达到控制精度，在力矩指令连续变化时，容易产生过学习现象，会造成系统发散。分析常规CMAC网络可知，误差被平均分配至所有激励的存储单元，经过多次迭代后，最初的存储单元中已经包含先前学习过的知识，应当具有更高的可信度，权值调整应该越小。因此将存储单元的学习次数作为学习的可信度，可信度越高，其权值调整越小。基于可信度的权值调整公式为：

(18)

f(j)是存储单元的可信度，记录了第j个存储单元的学习次数。

3 复合控制器设计

电动负载模拟器中，系统的输出力矩包含加载电机的输出力矩Tl和舵机扰动带来的多余力矩2部分，其中多余力矩主要是由舵机运动的角速度ω引起。为了更好地抑制系统的多余力矩，将系统的力矩偏差e和舵机的角速度当作复合控制器的输入，将基于可信度分配的CMAC网络和PID控制结合的复合控制结构，如图3所示。

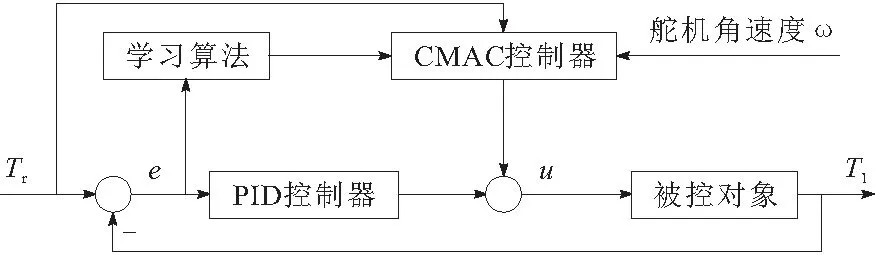
图3 CMAC和PID复合控制结构

CMAC采用有导师学习算法。在每一控制周期结束时，CMAC神经网络经过计算输出控制量un(k)，再和总控制输入u(k)进行比较，从而根据可信度原则调整权值大小，直到网络输出和总控制输入之间的偏差符合指标要求。

CMAC的调整指标为:

(18)

基于可信度分配的权值更新公式为：

(19)

w(k)=w(k-1)+Δw(k)+α(w(k)-w(k-1))

(20)

CMAC网络的控制输出为：

(21)

传统PID控制的输出量up(k)为：

(22)

最后得到系统总的控制输出量：

u(k)=un(k)+up(k)

(23)

4 仿真和试验

使用的加载系统试验台如图4所示，试验台主要包括4个加载通道，每个加载通道由加载电机、力矩传感器、编码器等组成。

图4 加载系统试验台

系统主要部件参数如表1所示。

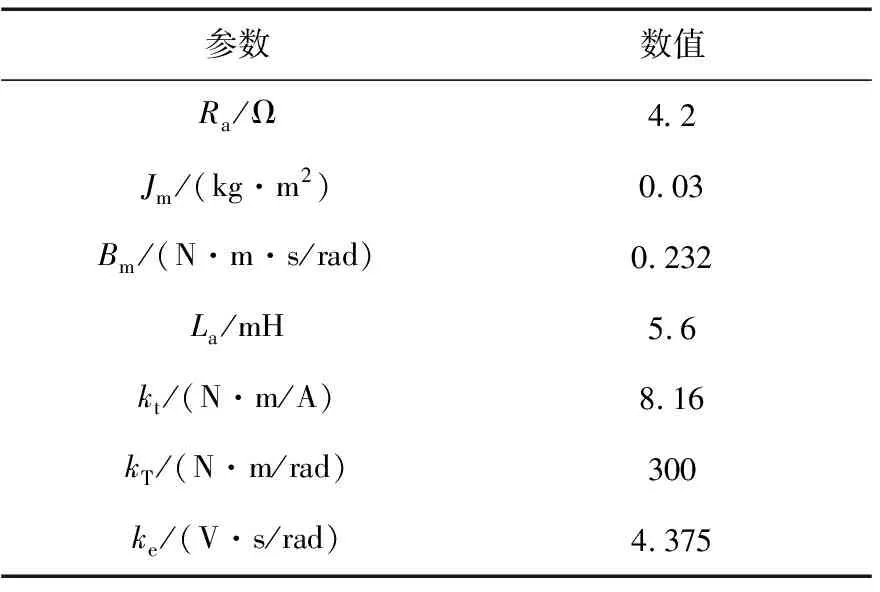
表1 加载系统参数

4.1 仿真实验

首先分析在未采用复合控制器时电机电动负载模拟器的多余力矩情况，给定力矩指令为零力矩，舵机位置伺服系统做幅值为2°，频率为10 Hz的正弦运动，电动负载模拟器系统产生的多余力矩,如图5所示。

接下来使用CMAC网络和PID复合控制器来进行电动加载，舵机运动保持不变，此时电动加载系统的产生的多余力矩，如图6所示。加载的初始时刻加载误差比较大，当CMAC学习过程结束之后，多余力矩稳定在0.4 N·m以内。

图5 电机负载模拟器的多余力矩

图6 加入复合控制器时的系统多余力矩

通过对比发现，传统电动加载仅仅采用PID控制策略系统产生的多余力矩为10 N·m左右，而引入CMAC和PID结合的复合控制器，电动加载系统的多余力矩仅为0.4 N·m，多余力矩仅为抑制前的4%，消除了大部分的多余力矩。从而证明了复合控制算法抑制多余力矩的有效性。

在电动负载模拟器试验平台进行验证，加载力矩指令为幅值10 N·m，频率10 Hz的正弦信号，舵机位置伺服系统做幅值为2°，频率为10 Hz的正弦运动，采用CMAC和PID结合的复合控制器进行正弦加载，如图7所示。初始时刻的加载误差比较大，当CMAC训练完成之后，载荷跟踪也趋于稳定，此时加载系统幅值误差为0.3 N·m，相位差为，符合加载系统的“双十指标”。试验结果表明，基于可信度分配的CMAC和传统PID复合控制能够有效抑制多余力矩，快速跟踪载荷，与仿真结果基本一致。

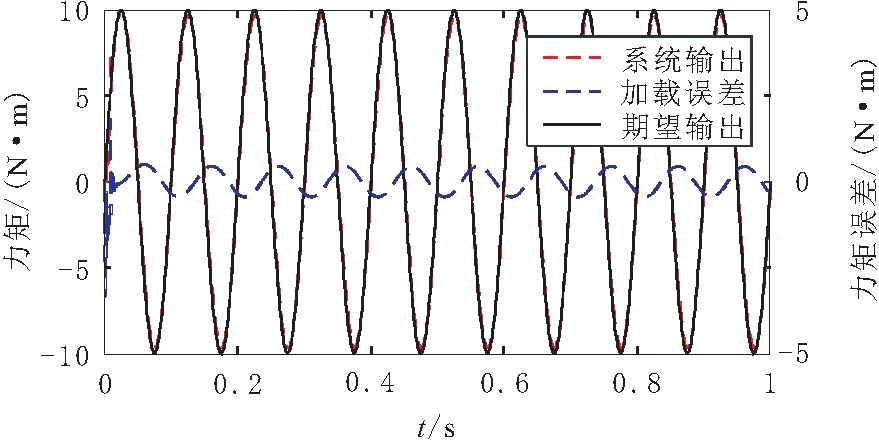
图7 正弦加载实验曲线

5 结束语

将CMAC网络和传统PID结合的复合控制器应用到电动加载，来抑制系统多余力矩和提高系统非线性抑制能力，并提出基于可信度分配的权值更新算法来抑制CMAC网络的过学习现象，仿真和试验结果均表明改进的CMAC和PID复合控制算法能够提高系统的鲁棒性，增强系统的加载精度。

参考文献：

[1] JIAO Z X, GAO J X, HUA Q, et al. The Velocity Synchro-nizing Control on the Electro-Hydraulic Load Simulator[J]. Chinese Journal of Aeronautics, 2004, 17(1):39-46.

[2] 黄勇,孙力,阎杰.连接刚度对电动负载模拟器性能的影响[J].弹箭与制导学报,2004,24(增刊7):170-173.

[3] 符文星,朱苏朋,孙力.弹簧杆刚度对电动负载模拟器的性能影响研究[J].弹箭与制导学报,2009, 29(2):286-288.

[4] LYU S S, LIN H, FAN M D.Electric loading system with multi closed-loop control[J].Electric Machines & Control,2015 ，19(9)：16-22.

[5] 任志婷, 焦宗夏.小转矩电动式负载模拟器的设计[J]. 北京航空航天大学学报, 2003, 29(1):91-94.

[6] 王权, 李军, 戴立.基于BP神经网络的电动伺服加载算法研究[J]. 工业仪表与自动化装置, 2017(2):8-13.

[7] 王修岩, 刘艳敏, 李宗帅.基于RBF神经网络和重复控制PID的电动负载模拟器复合控制[J]. 电力科学与技术学报, 2017, 32(1):84-89.

[8] YANG B, HAN H.A CMAC-PD compound torque controller with fast learning capacity and improved output smoothness for electric load simulator[J].International Journal of Control Automation & Systems,2014,12(4):805-812.

[9] 刘大磊.道路模拟试验台CMAC与PID复合控制仿真研究[D].杭州：浙江工业大学, 2009.

[10] 杨鹏,施光林,泮健.基于CMAC+PID复合控制的多缸力加载控制研究[J].液压与气动,2011(2):49-53.