基于制造误差的新型无同步齿轮液压振动锤同步性研究

罗春雷，黄松松，唐志清，陈珍颖，莫 鑫

（中南大学高性能复杂制造国家重点实验室，湖南，长沙 410083）

液压振动锤具有功率大、对环境污染小、作业质量好、噪音小、操作简便、可水下作业等突出优点，得到越来越广泛的应用[1]。然而，传统液压振动锤采用同步齿轮实现同步回转，存在着油液发热严重、润滑失效、齿轮频频受损、使用寿命过短等问题[2]。针对上述问题，本课题组提出了一种新型的液压振动锤——无同步齿轮的液压振动锤，其工作方式是通过系统之间的相互耦合作用，实现自同步振动，由于取消了同步齿轮的这种强迫同步方式，使得液压振动锤的工作性能得到有效改善。

目前，无同步齿轮液压振动桩锤的研究多集中于液压系统和桩土作用对系统同步性的影响，而机械结构方面对系统同步性影响的研究则比较欠缺。由于液压振动锤的同步运动是桩土作用、机械系统和液压系统相互耦合的结果，所以，在考虑桩土作用、液压系统的基础上，研究机械加工工艺和制造因素造成的双回转系结构之间的差异对液压振动锤同步运动的影响十分必要。考虑这三个方面开展自同步研究，国内外的研究并不多见。在机械方面，韩清凯[3]研究了激振器的偏心距、回转摩擦阻矩对自同步运动的影响规律，但没有考虑两回转系之间的差异对系统的影响，而且针对的是机电系统自同步理论研究，研究对象针对机电传动而不是液压传动；陈珍颖[4]研究了液压马达的结构差异造成的油液泄漏不同对同步运动的影响；陈晓哲[5]研究了激振源（电机）安装位置间距对同步运动的影响。在实际工程应用中，两回转系的机械结构不可避免地存在差异，其中偏心块的质量差异、回转轴系的摩擦系数差异对系统的同步性影响很大。因此研究两回转系偏心块质量差异和回转轴系的摩擦差异对无同步齿轮液压振动锤同步振动的影响显得十分必要。

本文建立了无同步齿轮液压振动锤的机电液系统耦合动力学模型，基于该模型，运用matlab/simulink进行数值仿真，研究耦合作用下双回转系偏心块的质量差异、回转轴系的摩擦系数差异对液压振动锤振动同步的影响规律，为进一步探索液压振动锤的自同步特性提供了依据，同时也为新型液压振动锤的设计提供了理论依据。

1 新型无同步齿轮液压振动锤系统建模介绍

新型无同步齿轮的液压振动锤方案如图1所示，该系统主要包括液压泵、电液比例系统、液压马达、双回转系转阻调节系统、双偏心质量块、振动锤箱体以及做功对象等。

图1 新型无同步齿轮液压振动桩锤系统模型Fig.1 System model of new hydraulic vibratory hammer without synchronous gear

系统运行时，由电比例阀1,2分别为液压马达1,2分配流量，而液压马达1,2分别驱动两个偏心质量块1,2反向回转。回转过程中，双偏心块产生的离心力在水平方向上相互抵消，而在竖直方向上相互叠加。竖直方向上的叠加力作为合力使振动锤和桩体产生位移，进行打桩作业。

由于两液压内部油液泄漏存在差异，偏心块的回转相位角不可能完全一致，回转过程中两偏心块会产生相位差。此时，通过传感器将偏心块的相位角反馈至控制系统，控制系统对电比例阀1,2的开口量进行微调，使相位超前回转系的液压马达流量减少而相位落后回转系的液压马达流量增加。一方面，由于双回转系驱动马达的油液压力是一样的，通过流量调节，使原先相位落后的回转系的驱动力矩相对增大，原先相位超前的回转系的驱动力矩相对减小；另一方面，通过调节转阻系数，原先相位落后的回转系的转阻力矩相对减小，原先相位超前的回转系的转阻力矩相对增大。

此外，由于地基土和振动锤自身弹性和阻尼的存在，双回转系并不是独立的，而是在运动中呈现相互影响、相互作用的关系，即双回转系之间有相互耦合作用。回转过程中相位落后的回转系的振动转矩将比相位超前的回转系的振动转矩低。在上述几种因素的综合作用下，原先相位落后的回转系的有效驱动力矩相对增大，偏心块的角加速度相对增大，而原先相位超前的回转系的有效驱动力矩减小，偏心块的角加速度相对减小。这样，原先相对慢的速度加快，原先相对快的速度减慢，双回转系的相位差减小。经过反复几次过渡后，双回转系的运动状态将趋于一致，即实现同步回转。

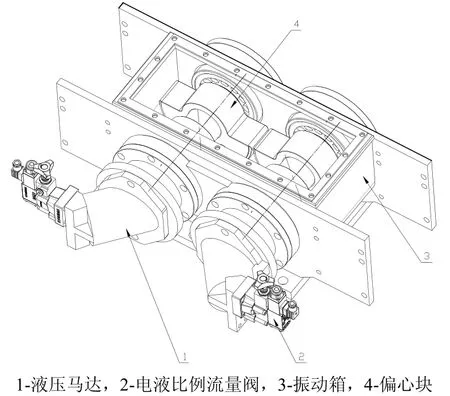
图2 新型无同步齿轮液压振动锤结构示意图Fig.2 Structure diagram of new hydraulic vibratory hammer without synchronous gear

由图2可知，回转系1是指由液压马达1驱动转轴1上的偏心块1进行回转。回转系2是指由液压马达2驱动转轴2上的偏心块2进行回转。

2 新型无同步齿轮液压振动桩锤系统数学建模

2.1 液压马达驱动回转系之间耦合振动微分方程

由图3可知，实际操作过程中，由于不能实现完全同步，双液压马达驱动的回转系回转时在平面坐标中应该会产生三个自由度的振动：其中在竖直方向上，偏心块的离心力合成激振力，带到振动锤及桩体周期性振动；在水平方向上，两个偏心块的离心力会合成水平分力，引起振动锤及桩体的侧振。同时，振动锤质心因扭矩的存在而产生扭振。但是，相对于竖直方向的激振力，水平分力和扭矩对振动锤及桩体的影响要小得多。因此在研究回转系之间耦合振动微分方程中，将其忽略不计。

图3 振动锤偏心块产生的激振力动力学简图Fig.3 Dynamic diagram of excitation force produced by the eccentric block of vibration hammer

为了推导出无同步齿轮液压振动锤回转系之间耦合振动微分方程，建立了振动锤双偏心块动力学简图所示（如图3）及平面坐标系XOY，双液压马达驱动偏心块做反向同步回转,水平方向分力抵消，液压振动锤及桩体只做纵向周期振动，其运动微分如下：

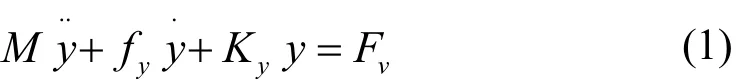
式中：M为振动锤箱体质量；y为桩锤系统垂直方向的位移；Ky为地基土和隔振弹簧的合成刚度；为地基土阻尼系数；Fv为偏心激振力。

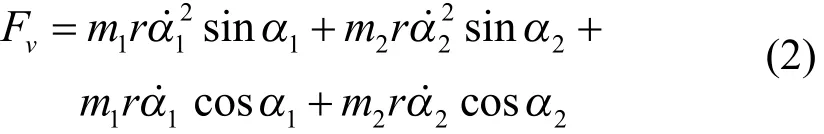
式中：为偏心块1的质量；为偏心块2的质量；r为偏心半径；分别为偏心块1、2的相位角。

上述等式中右侧分别为双偏心块在回转过程中产生的离心力和角加速度产生的惯性力在y方向合力，上述作用力叠加形成了无同步齿轮液压振动锤在竖直方向上的激振力。

可得双偏心回转系的微分方程：

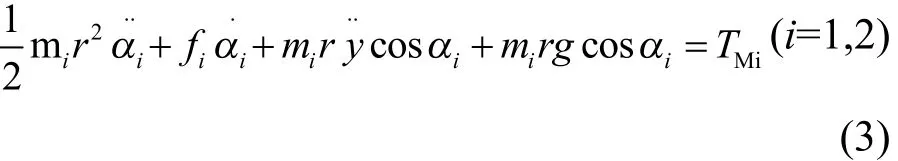
式中：分别为偏心系1、2的摩擦系数；分别为两液压马达作用于偏心块的有效力矩。

2.2 液压马达泄漏数学模型

如图4所示，轴向柱塞液压马达在工作运转中主要由三方面的因素决定马达的内部泄漏，分别是柱塞副泄漏、滑靴副泄漏及配流盘泄漏。

图4 轴向柱塞马达内部泄漏示意图Fig.4 Diagram of axial piston motor of internal leakage

在模型的搭建中，融入了液压马达模型，考虑了油液泄漏这个重要的影响因素。根据液压马达的建模分析过程[6]，可以得到马达同步系统的模型。同时，假设系统输入到两马达中的流量是相等的。

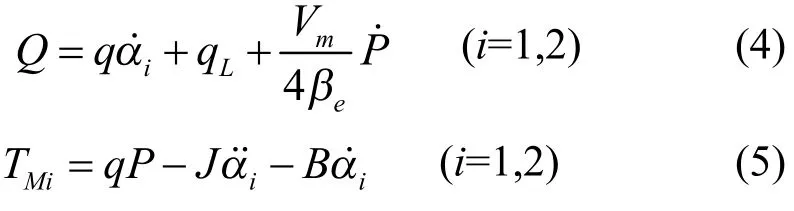
式中：q为马达排量；P为马达工作压力；J为马达轴的转动惯量；B为马达粘性阻尼系数；Q为输入马达总流量；为马达泄漏流量；表示马达进油腔与回油腔的总容积；为油液等效体积的弹性模量。

针对液压马达的各摩擦副泄漏进行具体分析。其中柱塞副泄漏属于偏心环形缝隙泄漏[7]，柱塞副泄漏损失流量为：

式中：i=1,2；d为柱塞的直径；为柱塞副的间隙值；η为液压油的动力粘度；ε为柱塞的偏心率，；为柱塞随马达转过的角度；l柱塞与柱塞副的接合长度；D为柱塞的分布圆直径；为柱塞相对于柱塞孔的运动速度；θ为马达斜盘的倾角。

马达泄漏主要是由柱塞副的泄漏引起的，但是配流盘和滑靴的泄漏同样不可忽视。其中滑靴副泄漏流量为：

式中：为滑靴副的油膜厚度；分别为滑靴及通油孔半径值；为供压比，此处设为1。

配流副泄漏损失流量为：

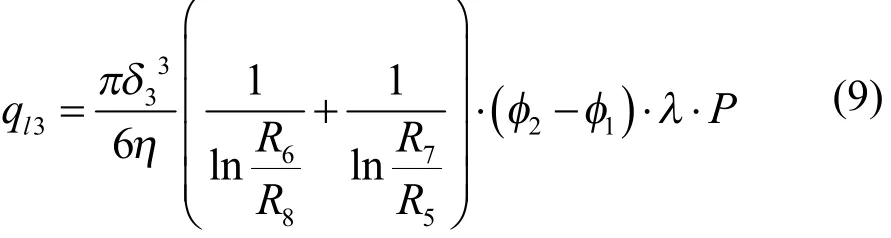
式中：为配流副的油膜厚度；分别为配流盘内外密封带半径；分别为配流盘静压支承的有关角度。

由以上各式可知，轴向柱塞马达的泄漏总量：

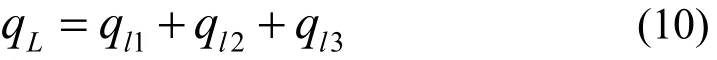
3 新型无同步齿轮液压振动锤同步特性分析

通过上述分析可知，振动锤的结构参数、液压系统两马达内部泄漏情况以及地基土的参数三方面的多种参数共同影响着系统的同步性。其中，振动锤的结构参数差异对双回转系的系统同步性影响显著。本文以MATLAB/Simulink作为仿真平台，采用龙格库塔算法对无同步齿轮液压振动锤系统的同步性进行数值计算研究，分析系统在机械系统的结构差异影响下的系统同步性，进而判定系统能否实现同步振动。同时，将液压振动锤的两个偏心块的相位差作为仿真输出，以系统能否实现同步振动作为条件，找出偏心块质量和回转轴系的摩擦在满足上述条件基础上的参数差异范围。液压振动锤系统参数采用以本项目组设计的ZZY40B型无同步齿轮液压振动锤，具体参数如表1。

表1 液压振动锤相关参数Table 1 The parameters of hydraulic vibration hammer

根据上节的各式可以建立系统的仿真模型，如图5所示，可以明确地反映出振动锤机械系统与液压系统之间的耦合关系，并可输出两个偏心回转系的实时相位差，通过To workspace模块将其值输入到Matlab工作空间，作为最终同步的判定依据。

根据式（2）可得有关激振力的仿真求解模型，如图6所示。其中激振力的微分方程封装在模型的子模块中。

根据式（4）～（10）可得液压系统的仿真模型，其中液压马达所受的转矩微分方程封装在子模块中。

图5 系统耦合模块Simulink仿真模型Fig.5 The Simulink simulation model of the system coupling module

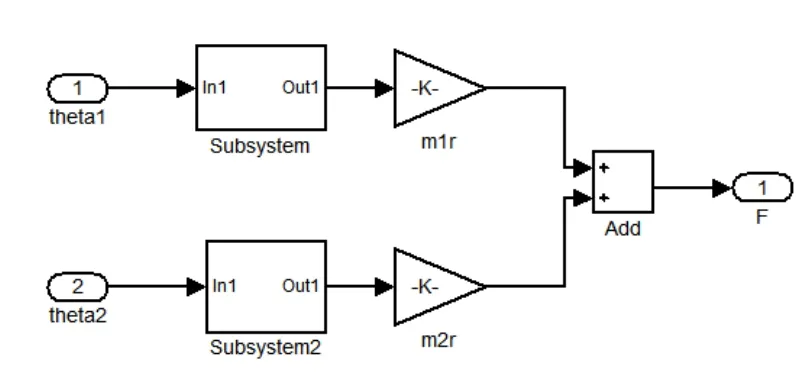
图6 激振力系统模块Simulink仿真模型Fig.6 The Simulink simulation model of the vibration force system module

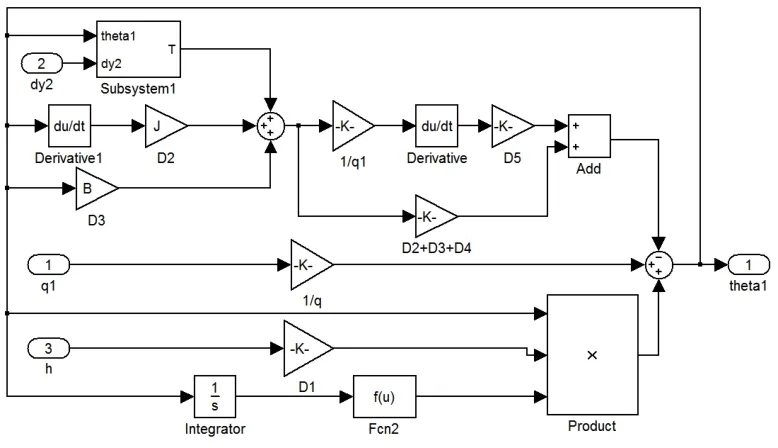
图7 液压系统模块Simulink仿真模型Fig.7 The Simulink simulation model of the hydraulic system module

根据以上各系统的模块以及式（1），可以建立起整个系统的仿真模型如图8所示，各个参数变量在系统间相互交换，最终模拟出液压振动锤各个系统耦合的结果。

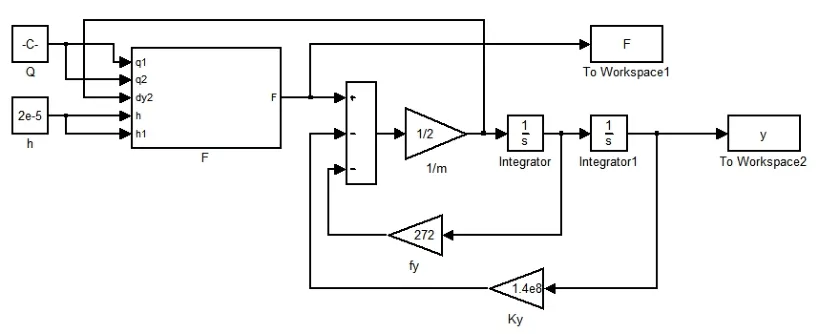
图8 无同步齿轮液压振动锤系统Simulink仿真模型Fig.8 The Simulink simulation model of the non- synchronized gear hydraulic vibratory hammer system

3.1 偏心块质量差异对同步运动的影响

由于制造加工的差异、生产环境等因素不可避免地造成偏心块的质量差异，在系统运行过程中，该差异对同步运动有一定的影响。为了更加直观地了解偏心块质量差异对系统同步性的影响，忽略偏心块质量变化对偏心距的影响，设置四组不同的偏心块质量，仿真时将其中回转系1中的偏心块质量设为80 kg，回转系2中的偏心块质量分别设置为81 kg、82 kg、83 kg、84 kg。然后在偏心块质量不同的取值上对两偏心块的相位差αΔ进行考察比较，分析偏心块质量差异对系统同步性的影响。

图9 =80 kg，=81 kg时的相位差Fig.9 =80 kg，=81 kg phase difference

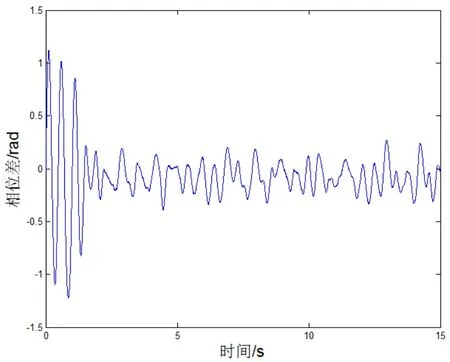
图10 =80 kg，=82 kg时的相位差Fig.10 =80 kg，=82 kg phase difference

图11 =80 kg，=83 kg时的相位差Fig.11 =80 kg，=83 kg phase difference

图9～图11所示为两回转系在不同偏心块质量状态下，两偏心块的相位差动态变化曲线。分析图9～图 11可知，当回转系 1中的偏心块质量为80kg、回转系 2中的偏心块质量为 80～83kg之间时，两偏心块的相位差经短时间过渡后，稳定到0rad附近，呈现持续小幅度振荡状态，液压振动锤可以实现同步振动。当两偏心块的质量之差加大时，两偏心块相位差变化的峰值增大。

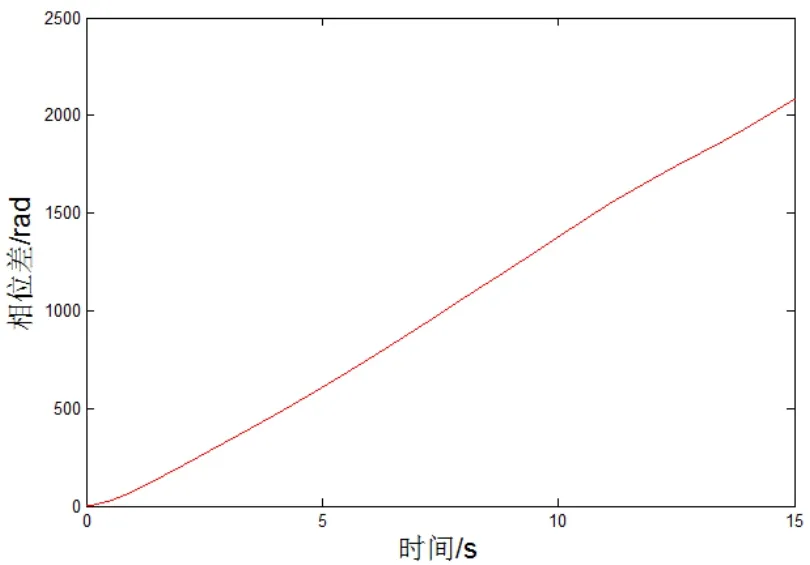
图12 =80 kg，=84 kg时的相位差Fig.12 =80 kg，=84 kg phase difference

图12所示为两回转系在不同偏心块质量之差较大的状态下，两偏心块的相位差动态变化曲线。分析图12可知，当回转系1中的偏心块质量为80 kg、回转系2中的偏心块质量为84 kg时，两偏心块的相位差发散。液压振动锤无法实现同步振动。

3.2 回转轴系的摩擦系数差异对同步运动的影响

关于加工误差方面，除了上述偏心块质量存在差异，两回转系的转轴的摩擦系数同样存在差异，而且该因素对系统同步性的影响最大[9]。同样仿真时将其中回转系1中的转轴摩擦系数ƒ1设为0.01，回转系2中的转轴摩擦系数ƒ2分别设置为0.012、0.014、0.016、0.018，然后分析转轴的摩擦系数差异对系统同步性的影响。

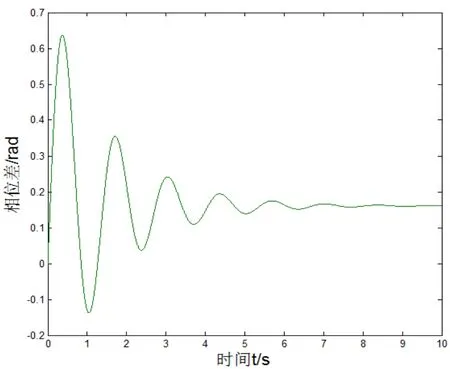
图13 =0.01，=0.012时的相位差Fig.13 =0.01，=0.012 phase difference

从图13～图15可以看出，曲线在短暂振荡后各自收敛到一个相对较小的数值。其中，当1，时，曲线振荡峰值为0.64 rad，相位差最终收敛为0.16 rad；而当1，时，曲线的振荡峰值则为1.17 rad，相位差最终收敛为0.28 rad；而当，时，曲线的振荡峰值则为1.87 rad，相位差最终收敛为0.4 rad。比较上述三组曲线，可见，在一定范围内，回转轴系的摩擦系数差值越大，系统的同步性越弱，越难实现同步振动。

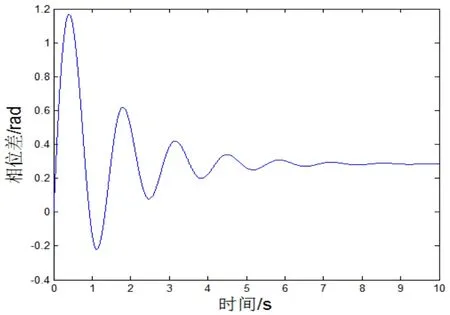
图14 ƒ1=0.01，ƒ2=0.014时的相位差△αFig.14 ƒ1=0.01，ƒ2=0.014 phase difference△α

图15 ƒ1=0.01，ƒ2=0.016时的相位差△αFig.15 ƒ1=0.01，ƒ2=0.016 phase difference△α

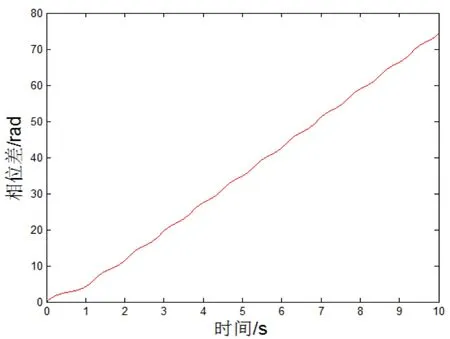
图16 ƒ1=0.01，ƒ2=0.018时的相位差△αFig.16 ƒ1=0.01，ƒ2=0.018 phase difference△α

从图16可看出，曲线迅速发散，当ƒ1=0.01，ƒ2=0.018时，两偏心块的相位差发散。液压振动锤无法实现同步振动。系统同步性消失，无法实现同步振动。

通过上述分析可知，当两回转系的偏心块质量和转轴的摩擦系数差异在一定范围内时，可以通过系统的耦合作用，消除差异对系统同步运动的影响，经过一定时间的振荡后，最终展现为同步状态。

4 试验

为了验证机械系统结构差异对系统同步性影响的预测结论，在位于长沙某建筑工地进行现场试验。试验装置由本项目组研制的ZZY40B型液压振动锤以及测试系统组成，所用的桩为钢板桩。第一组试验，选用一组偏心块，通过检测使偏心块质量均在80～83 kg范围内。将偏心块质量作为实验中的唯一变量，并在实验台开启前调整液压振动锤两偏心块，使初始相位差为零。启动试验台，利用传感器和测试软件分别测出液压振动锤两偏心块的相位差的变化情况。第二组试验，其它参数不变，仅改变偏心块质量，重复上述实验。同时，在每次实验开始之前，对两偏心块的初始相位差做调零处理。

上述实验所得相位差曲线分别如图17和图18所示。

图17 Δm=3kg时两偏心块的相位差Fig.17 Δm=3kg phase difference of two eccentricity masses

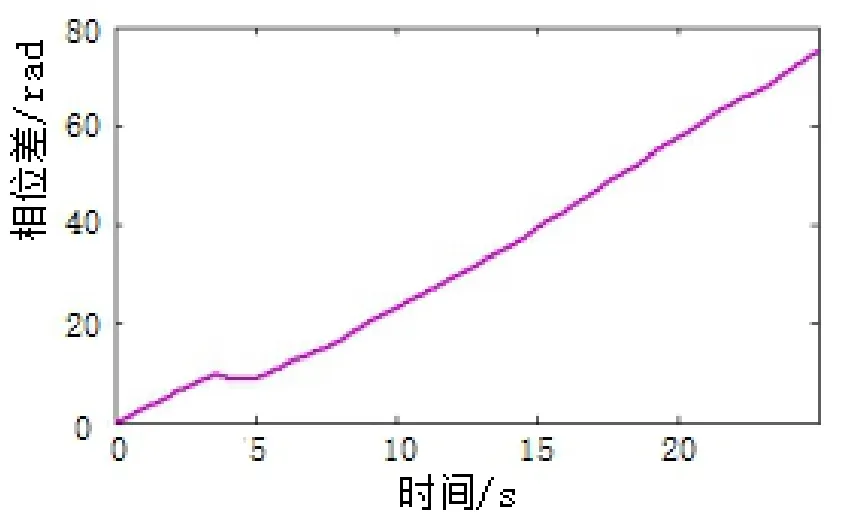
图18 Δm=4kg时两偏心块的相位差Fig.18 Δm=4kg phase difference of two eccentricity masses

试验结果表明，当两偏心块质量差值在Δm = 3 kg时，两偏心块相位差经过5.3 s过渡后稳定在0～0.8 rad之间振荡，振动锤可以实现同步振动；但是如果两偏心块质量差值超过上述范围，达到Δm = 4 kg时，相位差将快速发散，振动锤不能实现同步振动。对比仿真结果，当Δm = 3 kg时，系统过渡时间分别为4.8 s和5.3 s；相位差的收敛范围分别为0～0.5 rad和 0～0.8 rad，试验与仿真结果的相对误差不超过5%。而Δm = 4 kg时，相位差均在短时间内快速发散，系统无法实现同步振动。综上所述，试验结果与仿真的理论预测对比分析表明，试验结果与理论分析基本一致。

5 结论

本文建立了无同步齿轮液压振动锤的系统耦合模型，并基于该模型，对其进行仿真分析，得出了机械系统方面的结构差异对系统自同步的影响规律，同时直观地反映出两回转系的偏心块质量与转轴的摩擦差异在一定范围内时，系统可以通过内部的耦合作用，同样可以达到同步振动的状态，即相位差经过一定时间的振荡后，最终稳定在一定值。

试验结果与理论仿真分析基本一致，进一步完善了无同步齿轮液压振动锤的自同步理论研究，同时为液压振动锤的设计与选型提供了理论依据。

[1]闻邦椿,李以农,张义民,等.振动利用工程[M].北京：科学出版社,2005.

[2]范增辉. 双马达振动锤关键参数设计与同步控制研究[D].长沙:中南大学,2013.

[3]韩清凯,杨晓光,秦朝烨,等. 激振器参数对自同步振动系统的影响[J].东北大学学报:自然科学版, 2007,28(7):1009-1012.

[4]罗春雷,陈珍颖. 基于土壤滞回特性的液压振动锤自同步研究[J]. 计算机仿真, 2017, 34(2)：264-269.

[5]陈晓哲,孔祥希,窦景欣,等. 双机振动系统的自同步过程分析与试验研究[J].东北大学学报:自然科学版,2017, 38(1)：76-80.

[6]王占林.近代电气液压伺服控制[M].北京:北京航空航天大学出版社,2005.

[7]范芳洪,钟振龙,石金艳. 轴向柱塞马达柱塞副泄漏流量的计算与分析[J].液压气动与密封,2010,30(10)：21-22.

[8]翟培祥.斜盘式轴向柱塞泵设计[M]. 北京:煤炭工业出版社,1978.

[9]罗春雷. 液压振动桩锤沉桩动力学及调频调矩控制研究[D]. 长沙:中南大学机电工程学院, 2005.

[10]刘指先. 四轴液压振动桩锤的同步特性及其控制研究[D].长沙:中南大学机电工程学院, 2011

[11]罗春雷,韩清凯. 液压驱动控制的偏心回转系统同步特性[J]. 机械工程学报, 2010, 46(6)：176-181.

[12]Wen B C. Research concerning frequency entrainment of nonlinear self-synchronous vibrating machines[J].In Proceedings of International Conference of Nonlinear Oscillations, Kiev, USSR, 1981.

[13]Zhao C Y, Zhao Q H, Gong Z M .Synchronization of two self-synchronization vibrating machines on an isolation frame[J].Journal of sound and vibration,2011,27(6):73-81.

[14]范增辉. 双马达振动锤关键参数设计与同步控制研究[D].长沙:中南大学,2013.

[15]来鑫,乌建中,周文,等. 桩锤同步振动系统的机电耦合特性及同步控制[J]. 同济大学学报:自然科学版,2012(6):920-925.