关于广义Taylor 中值定理中间点函数可微性的进一步讨论

张芯语，张树义

（渤海大学数理学院，辽宁，锦州 121013）

Azpeitja[1]研究了Taylor公式“中间点”的渐近性质。同时，Jacobson[2]建立积分中值定理的类似的结果。在这之后，一些作者研究各种中值定理“中间点”的渐近性质，可见文献[3-18]。最近，我们在文献[19-26]中研究了包括广义Taylor中值定理在内的几种中值定理的“中间点函数”的一阶可微性。其中文献[18]研究了 Cauchy中值定理“中间点函数”

在x=a处的可微性且(a)=。文献[19]和文献[20]在一定条件下分别建立了泰勒公式和广义Taylor中值定理的“中间点函数”在x=a处的可微性且文献[21]在一定条件下建立了 Cauchy中值定理“中间点函数”在x=a处的可微性且文献[22]建立了广义中值定理“中间点函数”(x)

在x=a处的可微性且文献[23]建立了高阶 Cauchy中值定理“中间点函数 ”在x=a处的可微性且文献[24]利用比较函数概念, 建立了泰勒公式“中间点函数”的渐近性进而推出了文献[19]的可微性结论。文献[25]建立了积分中值定理“中间点函数”在x=a处的可微性文献[25]建立了第二积分中值定理“中间点函数”在x=a处的可微性且

本文的目的是进一步研究广义 Taylor中值定理“中间点函数”的可微性，在一定条件下获得了广义Taylor中值定理“中间点函数”在x=a处的可微性且显然此结果推广了文献[18-21]中的相关结果(事实上取α= 0 ,n=γ= 1 便得文献[18]中的结果；取α= 0 ,γ=λ,g(x) = (x-a)n便得文献[19]中的结果；取α= 0 ,γ=λ便 得 文 献[20]中 的 结 果 ； 取α= 0 ,γ=λ,n= 1 ,便得文献[21]中的结果) 。

广义Taylor中值定理设a和b是实数且a＜b，f,g。如果函数f满足

(i) 在上具有直至n- 1阶连续导数；

(ii) 在(a,b)内存在n阶导数且，则存在一点c∈(a,b)，使

设I是R上一区间，a∈I是I上一点，函数。如果函数f与g在I上n次可微，则由广义Taylor中值定理，，在以a,x为端点的开区间上，存在一点，使

如果不是单射的，则使(1)成立的点，一般不是唯一的。如果对，在以a,x为端点的开区间上选取一个cx，使(1)成立，那么也可以定义函数c:I-为，使(2)成立。

定理1[20]设I是R上一区间，a∈I是I上一点. 函数f,g:I→R。如果函数f与g在I上n次可微，则存在一函数c:，使得(2)成立。此外如果是单射的，则点是唯一的。

因为,，所以。于是可定义“中间点函数”显然在点x=a连续。

容易证明下列引理成立。

引理1设I是R上一区间，a∈I是区间I的左端点，在I上n次可微且

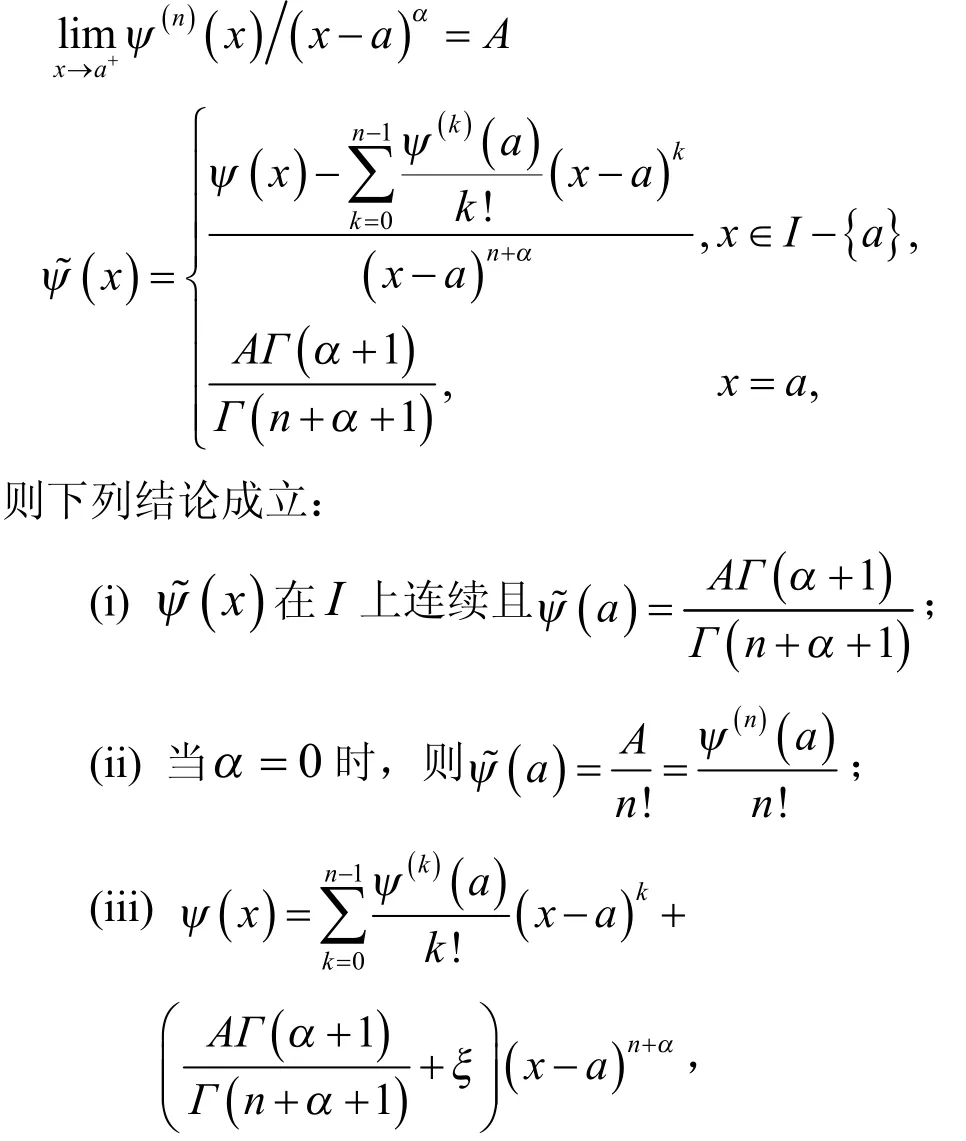
其中A是一常数,α是实数α＞-1，。

注1因为a∈I是区间I的左端点，所以在点a处连续是指在点a右连续。由于因此在点a右连续。

1 主要结果

定理2设I是R上一区间，Ia∈ 是区间I的左端点，函数满足下列条件：

(i) 函数f与g在区间I上有n阶导数且

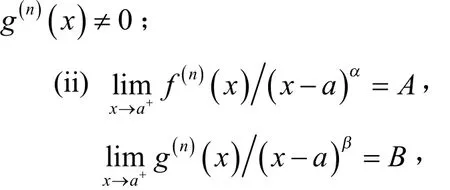
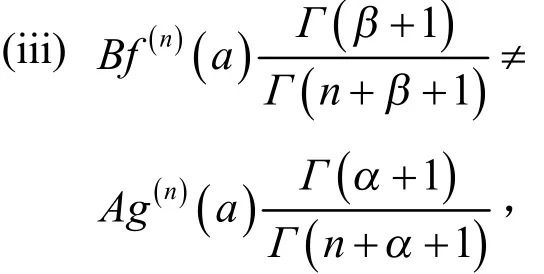
其中A,B是非零常数，α,β是实数α＞-1,，且α≠β，则下列结论成立：

存在实数，使，且

有下列性质：

证明由定理2条件和引理1，有

由上面等式，可推出

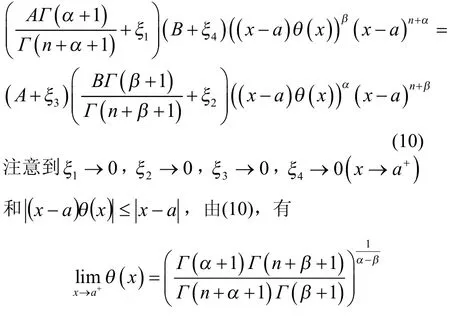
结论由推出。定理2证毕。

如果α=β，则定理2不再成立，但有：

定理3设I是R上一区间，a∈I是区间I的左端点，函数满足下列条件：

(i) 函数f与g在区间I上有n阶导数且；

有下列性质：

c) 对于任意，有

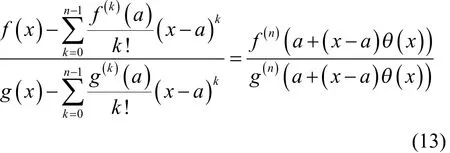
d) 存在极限

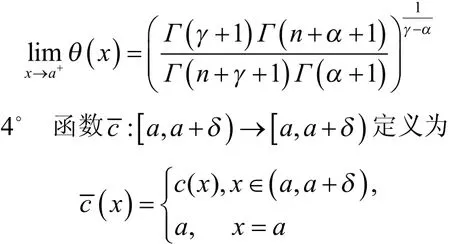
在x=a 可微且

证明首先指出定理3 的条件保证了γα≠。事实上, 若γα=, 则

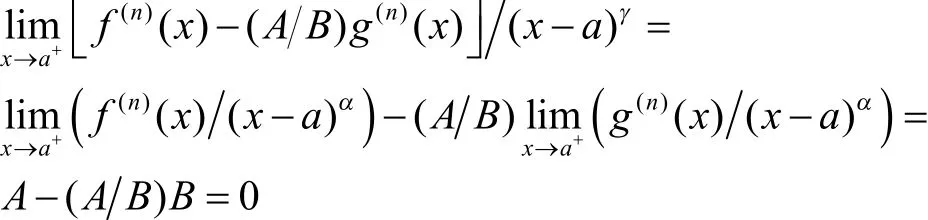
与此极限值相矛盾，故。

因 此 存 在 一 实 数δ＞0， 使且，有。

2°因为，所以在上严格单调，进而是单射, 因此存在唯一函数, 使得(11)成立。

a) 由(11)和(12)即得证。b) 由引理1，有

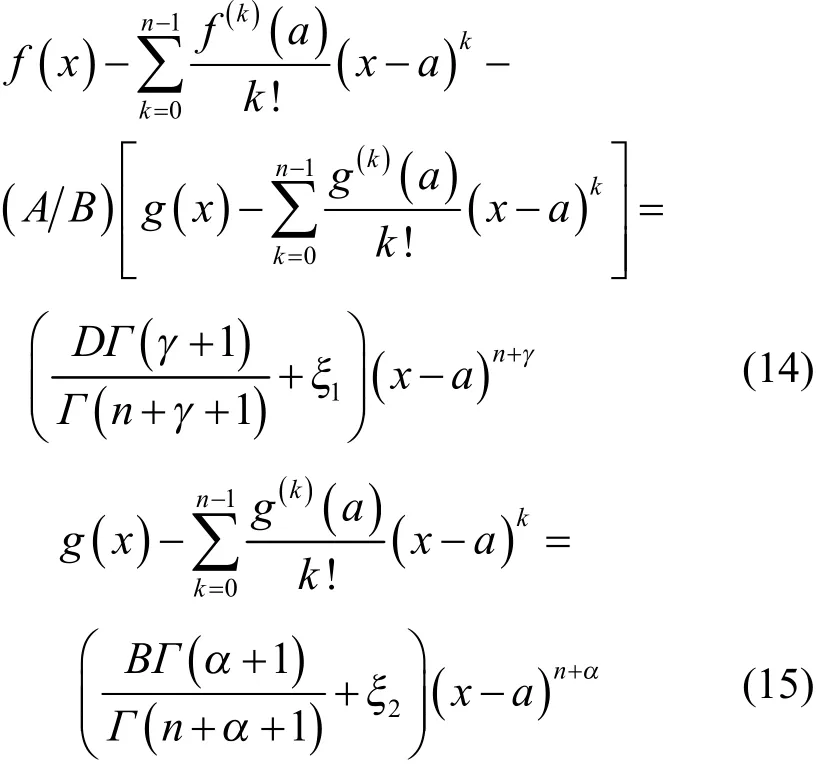
其中,。由条件(ii)，得

其 中,。 把(14)-(17)代 入(13)，并简单运算得

结论由推出，定理3证毕。

注2由于中的条件，只保证存在唯一函数，使(11)成立，因此在定理 3中如果α=0,γ=1，则该条件可以用代替。事实上, 当α=0,γ=1时，则。由引理1得

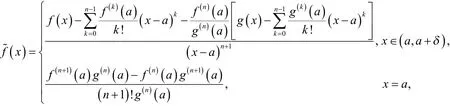
进一步，如果函数与在I上可微，则由洛必达法和导数极限定理，有

由此推出

从而是单射，于是当α=0，γ=1时由定理3可得如下结果。

定理4[20]R上一区间，a∈I是I的左端点。f,g:I→R是两个函数，满足下列条件

(i) 函数f，g在I上n+1次可微；

(ii) 对于所有，；

(iii)，则下列结论成立：

存 在 一 实 数， 使，，有并且 是单射的。

2°对于任意，存在唯一函数，使

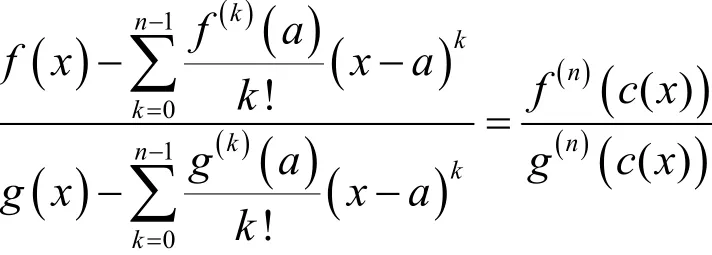
函数定义为

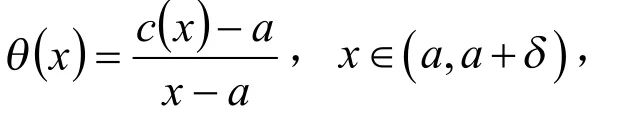
有下列性质：

e) 对于任意，有

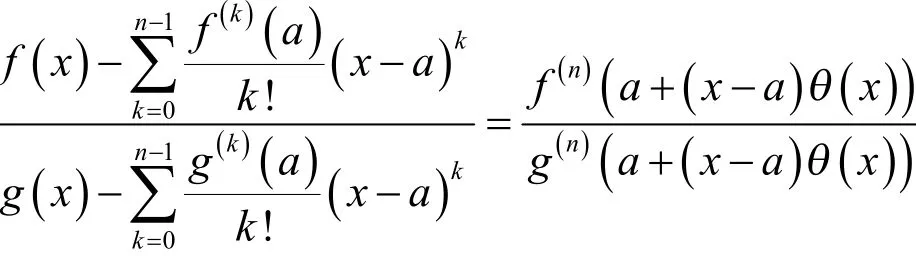
f) 存在极限

在x=a 可微且

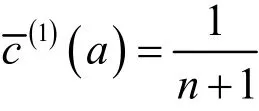
下面我们指出由定理3可推出文[20]中的定理2。

在定理3中取α= 0 ,γ=μ,则A=,。由引理1得

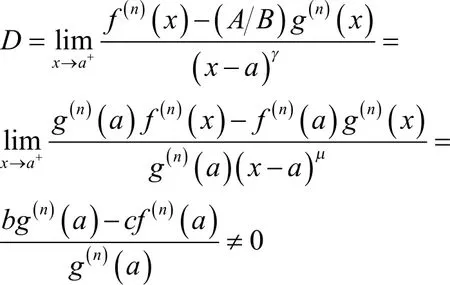
由引理1得

进一步如果函数与在I上连续可微，则由洛必达法和导数的定义，有

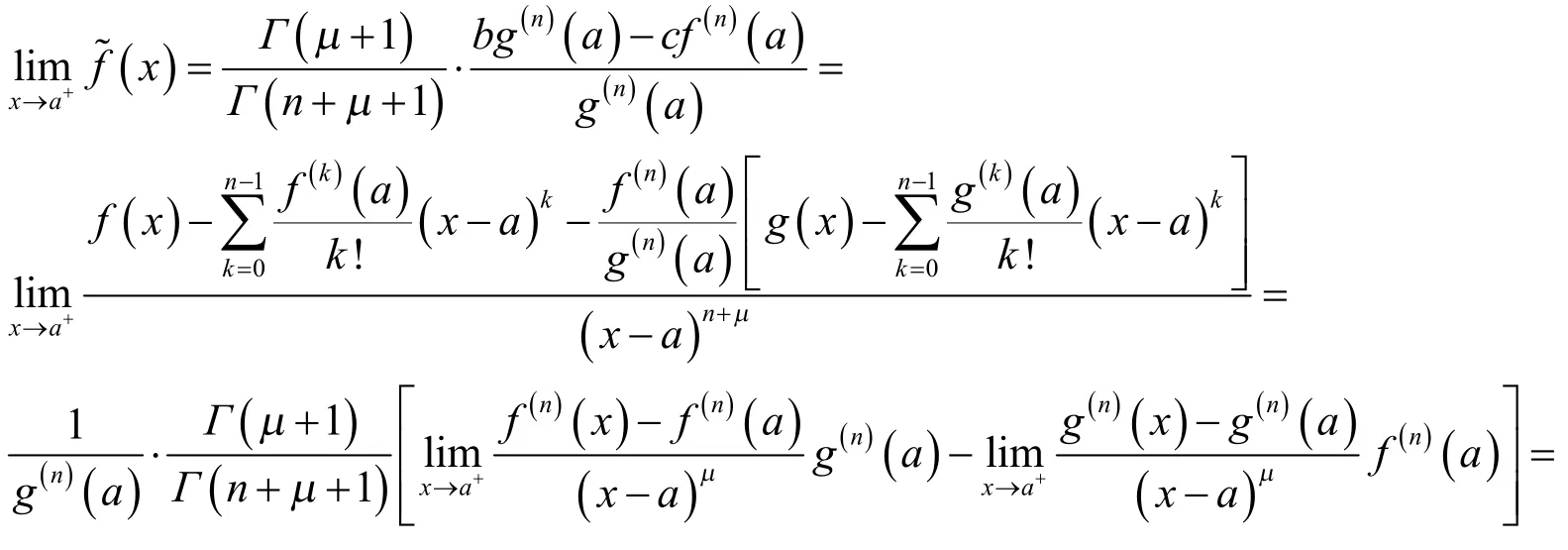
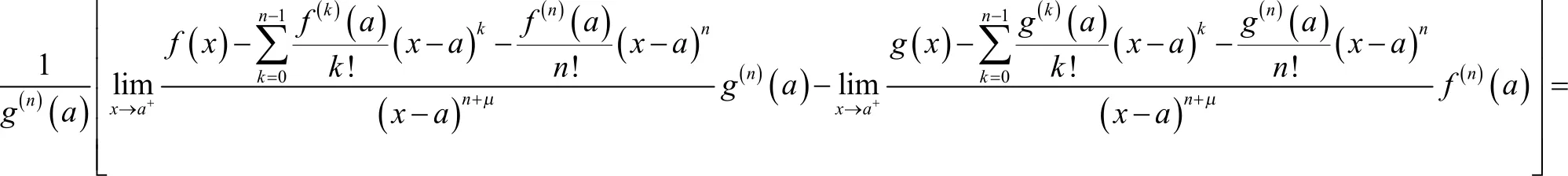
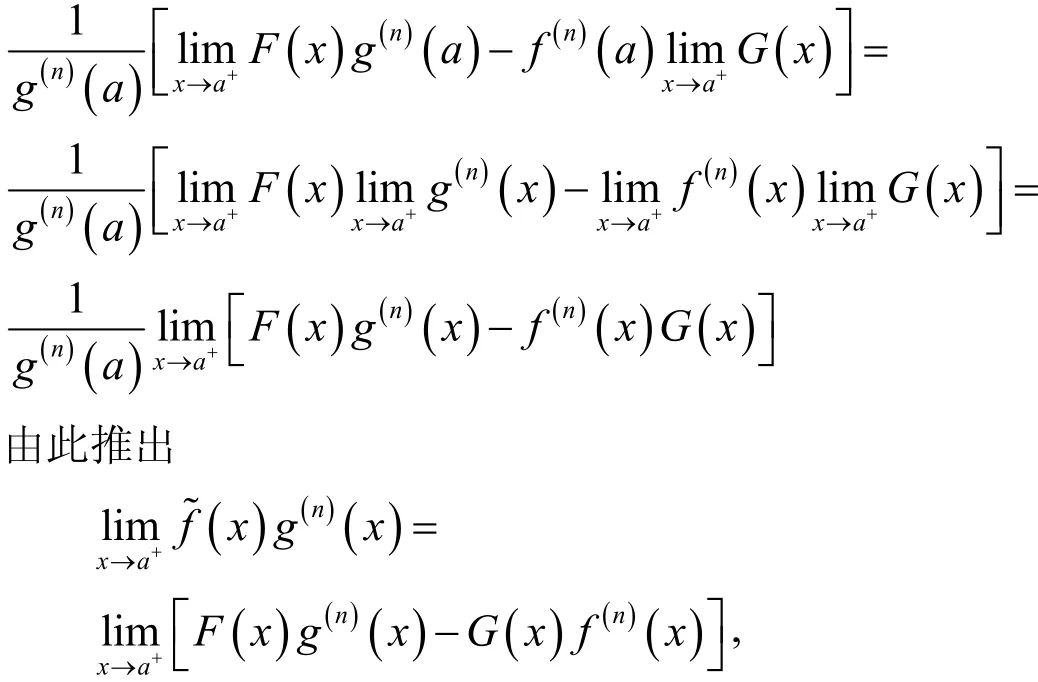
于是当α= 0 ,γ=μ时由定理3可得如下结果。

定理5[20]设I是R上一区间，a∈I是区间I的左端点，函数满足下列条件：

(i) 函数f与g在区间I上有n阶连续导数且；

(ii)存在实数α＞0，使

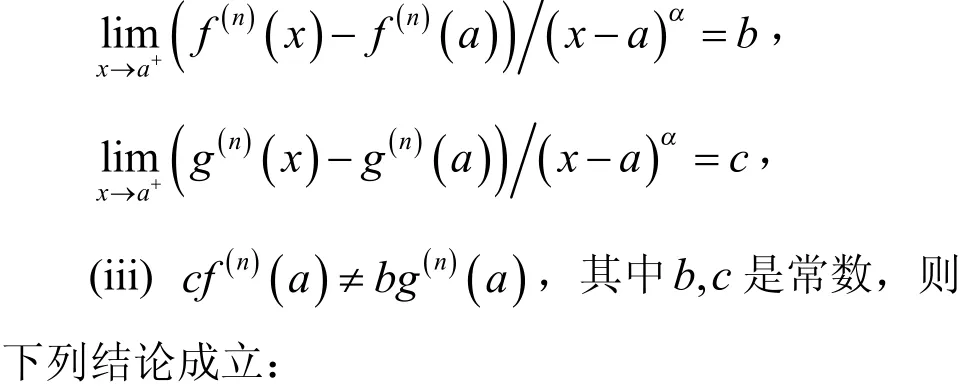
存在实数，使，且，有

, 其中

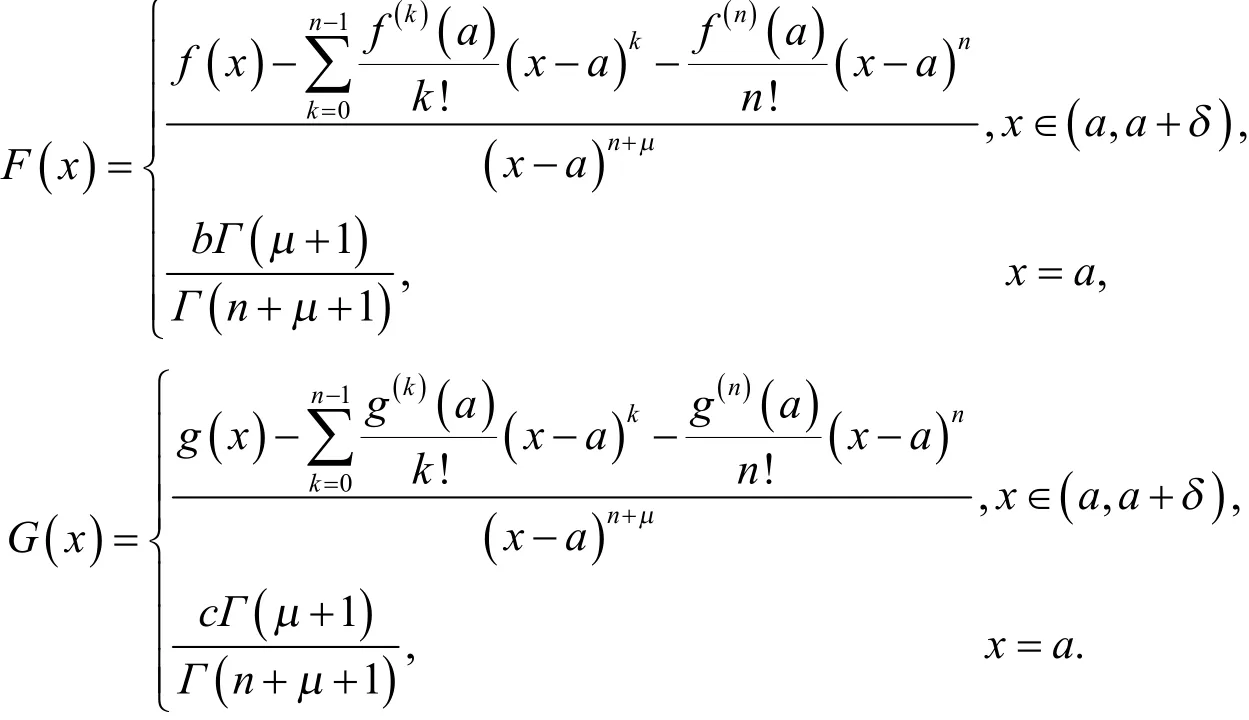
若再设,, 则对于任意， 存在唯一函数，使

函数定义为

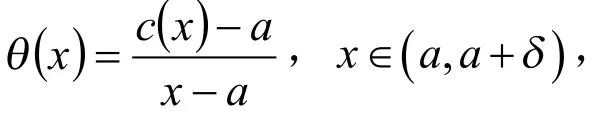
有下列性质：

g) 对于任意，有

h) 存在极限

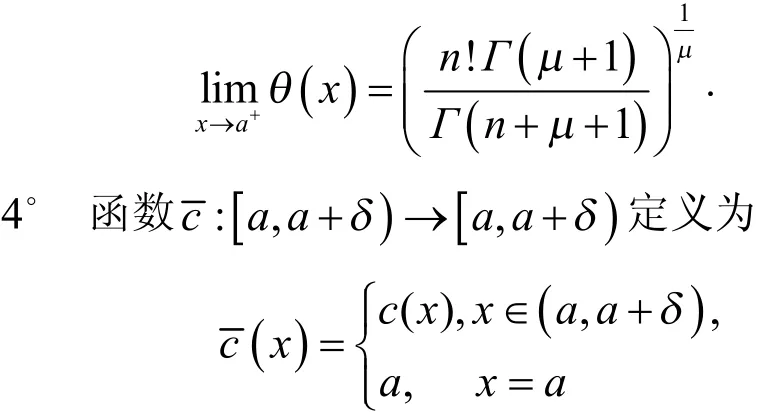
在x=a 可微且

需要指出的是由于是区间I的左端点，因此本文所涉及函数在点a的导数均为右导数。

[1]Azpeitja A G. On the Lagrange remainder of the Taylor formula[J]. Amer. Math. Monthly, 1982, 89(5): 311-312.

[2]Jacobson B. On the mean value theorem for integrals[J].Amer. Math. Monthly, 1982, 89(5): 300-301.

[3]张树义. 广义Taylor公式“中间点”一个更广泛的渐近估计式[J]. 数学的实践与认识, 2004, 34(11): 173-176.

[4]Duca D I. A note on the mean value theorem[J]. Didactica Matematicii, 2003, 19: 91-102.

[5]Mera R. On the determination of the intermediate point in Taylor's theorem[J]. Amer. Math. Monthly, 1992, 99:56-58.

[6]Powers R C, Riedel T, Sahoo P K. Limit properties of differential mean values[J]. J. Math. Anal. Appl. 1998,227: 216-226.

[7]张树义,赵美娜,郑晓迪.积分中值定理中间点的渐近估计式[J]. 北华大学学报:自然科学版, 2016,17(4):448-454.

[8]万美玲,张树义. 二元函数 Taylor公式“中间点”的渐近估计式[J]. 鲁东大学学报:自然科学版,2016, 32(2):1-4.

[9]张树义. 中值定理“中间点”的几个新的渐近估计式[J].烟台师范学院学报:自然科学版, 1995,11(2):109-111.

[10]张树义. 关于中值定理“中间点”渐近性的若干注记[J].烟台师范学院学报:自然科学版,1994,10(2): 105-110

[11]林媛, 张树义. 广义泰勒中值定理“中间点"当x→∞时更广泛的渐近估计式[J]. 南阳师范学院学报:自然科学版,2016, 15 (3): 1-5.

[12]张树义. 积分中值定理“中间点”更广泛的渐近估计式[J].南阳师范学院学报:自然科学版,2005, 4(3).15-19.

[13]张树义. 广义中值定理当m≠n时“中间点”的渐近估计式[J]. 南阳师范学院学报:自然科学版, 2006, 5(12):20-22.

[14]张树义. 关于中值定理“中间点”渐近性研究的新进展(I)[J]. 南都学坛,2000(6): 13-20.

[15]张树义. 积分中值定理“中间点”当x→∞时的渐近性态[J].沈阳师范学院学报:自然科学版,1998,(1):8-11.

[16]张树义. 中值定理“中间点”当x→+∞时的渐近性态[J].河北师范学院学报:自然科学版,1997,(3):4-7.

[17]刘冬红,张树义,郑晓迪. 二元函数柯西中值定理“中间点”的渐近估计式[J]. 井冈山大学学报:自然科学版,2017, 38(4):13-17.

[18]Duca D I, Pop O. On the intermediate point in Cauchy's mean-value theorem[J]. Math. Inequal. Appl., 2006, 9:375-389.

[19]赵美娜,张树义,郑晓迪. 泰勒公式“中间点函数”的一个注记[J]. 鲁东大学学报:自然科学版,2016,32(4):302-306.

[20]赵美娜,张树义,郑晓迪. 广义 Taylor中值定理“中间点函数”的性质[J]. 南通大学学报:自然科学版, 2016,15(3): 80-85.

[21]李丹,张树义,郑晓迪. Cauchy中值定理“中间点函数”的一个注记[J]. 南阳师范学院学报:自然科学版, 2016, 15(12): 5-11.

[22]张树义,林媛,郑晓迪. 广义中值定理中间点函数的性质[J].北华大学学报:自然科学版, 2016, 17(6) 714-719.

[23]张树义,丛培根,郑晓迪. 高阶 Cauchy中值定理中间点函数的性质[J].北华大学学报:自然科学版,2017, 18(1):19-24.

[24]李丹,张树义. 关于泰勒公式中间点函数的可微性[J].井冈山大学学报:自然科学版, 2016, 37(6)：11-14.

[25]刘冬红,张树义,丛培根. 积分中值定理中间点函数的性质[J]. 北华大学学报:自然科学版,2017, 18(4): 434-438.

[26]李丹,张树义,郑晓迪. 第二积分中值定理中间点函数的性质[J]. 南阳师范学院学报:自然科学版, 2017, 16 (6):5-8.