优美树的扩充

喻 卫

（安徽三联学院基础部，安徽，合肥 230601）

0 引言

关于优美树的讨论是数学家 G.Ringel在 1963年和1966年A.Rosa的一篇论文中提出的，在之后很多数学家在这方面作了大量的工作；并且于1996年由A.Rosa提出了著名的优美树猜想（在文献[1]的第十五个未解决的问题）；几十年来国内外许多学者从各方面研究此问题[2-11]。本文在前人基础之上进行讨论，扩大了优美树的种类。文中所讨论的图都是无向图，分别表示图G的顶点集和边集。未给出的记号和定义见参考文献[9]。

定义1一棵有n个顶点的树T,若存在集合{0,1,2,3,4,… ,n-1}分配给它顶点的一个标号为θ，使得由(uv)=定义的边诱导标号分配给各边以不同的标号，则称树T是优美的。

定义2两棵树在根点处用一条线相连，形成的图称之为树的根积。n棵树T的根积记为，另外定义中的子树按逆时针标上，并记根点u的那棵树为（见图 1）。

定义3n棵树T的根点(即对称点)同时与一个顶点连接，形成的树称为n棵树T的根和，记为nT。

定义4G是一个非空集合，优美树，且优美树T对于加法、乘法具有封闭性。单位元为空图，逆元为，则称G为一个优美树群。

乘法即在根点处用一条直线相连（见图1）。加法即在任意多棵同构树之间添加一个原点然后分别与根点连接（见图2）。

图1 n棵树T的根积记为Fig.1 The root product of n tree T is recorded as

图2 n棵树T的根和记为Fig.2 The root sum of n tree T is recorded as

定义5一棵树存在一条割边，能使割边分开的两部分完全一样，则称这样的割边为完全割边。

定义6一棵树存在一个这样的一个割点，能使割点分开的左侧和右侧完全一样，则称这样的割点为完全割点。

定义7一棵树在某一顶点或者在某一边进行一刀切，使得分成两边的树完全重合在一起，则称这样的树为完全对称树（见图3，图4）。

图3 关于边的完全对称树Fig.3 On the complete symmetric tree of edges

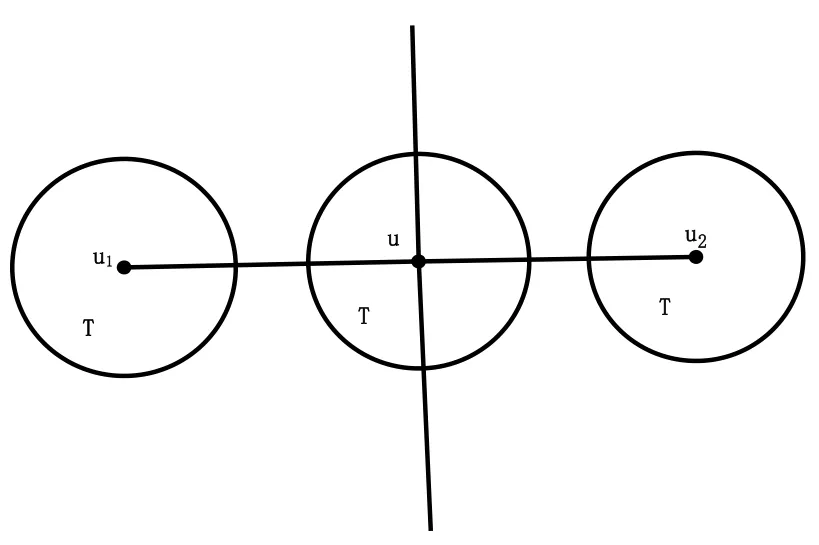
图4 关于点的完全对称树Fig.4 On the complete symmetric tree of points

1 主要结果及其证明

定理1是优美树。

证明树T的顶点数为m。树T的优美标号为f，边集为E。的顶点标号为。

下面给出的标号：

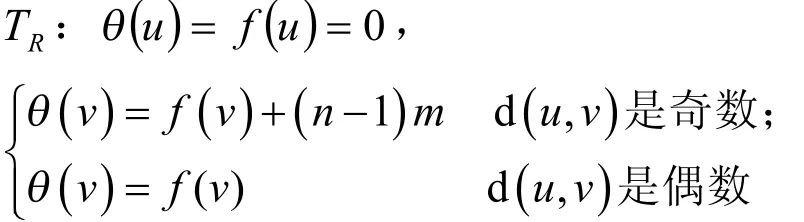
对于中n为偶数时；

下面证明θ是优美标号。

事实上，根据上述标号可知，树的顶点标号满足，，有。

为方便起见，记树边的诱导标号集合为根点组成的边诱导标号集合为树边的诱导标号集合为，即

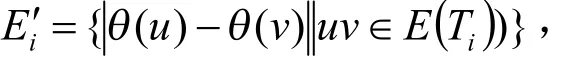
则

其中u满足是奇数；v满足是偶数。

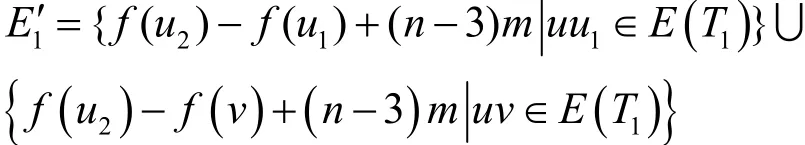
其中u2满足是奇数；v满足是偶数；u1是T1的根点。

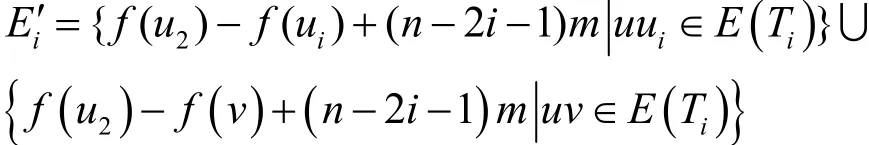
其中，u满足是奇数；v满2足是偶数；ui是Ti的根点。

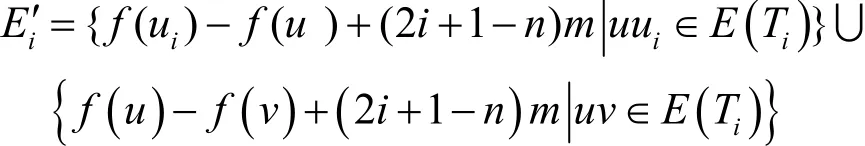
其中，u满足是奇数；v2满足是偶数；是根点。

所以每条边互不相同且

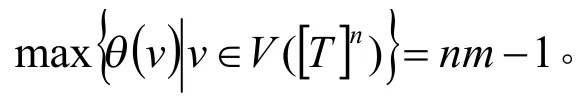
故θ是优美标号，即是优美树。

对于中n为奇数时；下面给出优美标号，证明同上。

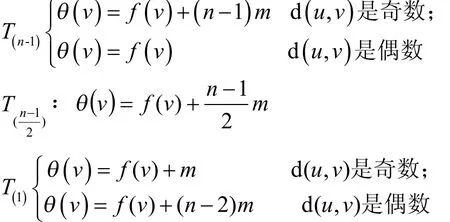
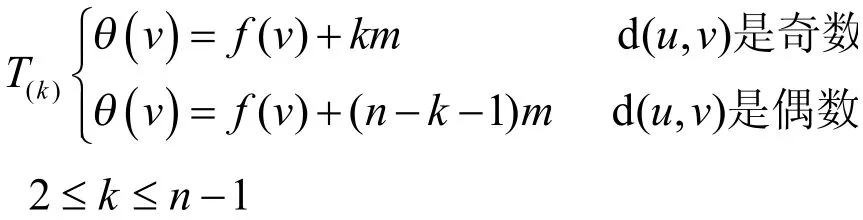
所以是优美树。

定理2是优美树。

下面给出的标号：

那张状子写道：“列国纷争，尚有移民移粟；天朝一统，何分江北江南。”对仗工整，说理透彻，令人拍案叫绝。由此可见，讼师们的智慧的确不容小觑。

,w是原点。

下面证明θ是优美标号。

事实上，按上述标号给每个顶点标号，可得出：

同样标记每条边的诱导标号集=，有

下面证明每条边是互不相同的。

证明同定理1。

对于nT中n为奇数时；

下面给出优美标号，证明同上。

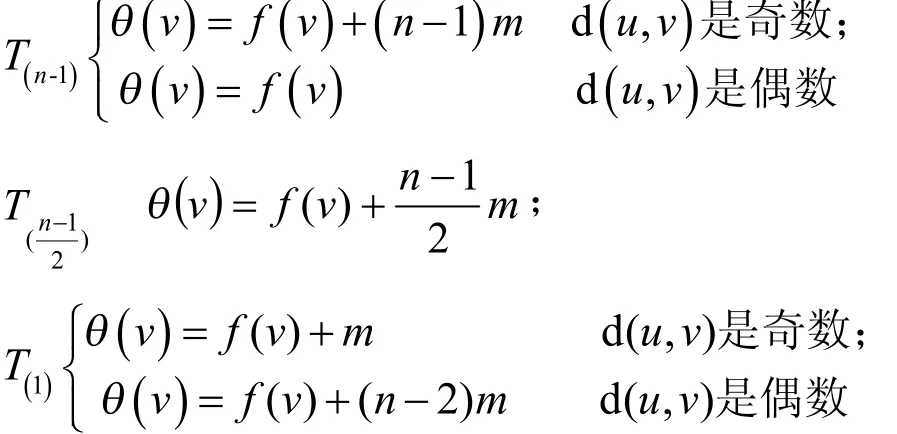
定理3 G是一个优美树群。

证明由定理1知一棵优美树T在群中的乘法具有封闭性。由定理2知在群中的加法也具有封闭性。群中的单位元是空白图（即没有点和边的图）用记号T0表示。群中的逆元是，故优美树对加法与乘法构造的集合是一个优美树群。

定理4在优美树群中的元素合成是一棵新的优美树的充分必要条件是每个组成部分都是优美的。

证明在代数中任意一个多项式都可以表示成

则在优美树群中任何一棵新的优美树都可以分解成

证明必要性：

因为，，…，是优美的。

当,…中只有一个不为0时，由定理1和2知定理成立。

当,… ,中至少有两个不为0时，不妨假设不等于0。

则证明构成的是一棵优美树。

由定理1的优美标号知，每棵子树的根点分别为,,… ,，原点为。

结合定理1，定理2的标号知，所要证明的问题转化成(… ,,w)的标号是m优美标号序列，

又因为这些点构造而成的直径是为5的树，直径为5的树是优美的[3]，故这些根点标号构成了一个m优美标号。所以在由加法的标号知，形成新的树是优美的，其中根点必然与原点连接。

下面证明：

由群中的加法知：在图中添加一些直径为2的子树与根点邻接，整个图就构造成直径为5的树。由直径为5的树是优美树知，是优美树，必要性证毕。

证明充分性：

由定理1知道任意直径为或者5的树经过加法和乘法法则形成的树是优美的。现在在优美树群中把这样构造而成的树进行分解，看分解而成的每一部分的子树是否是优美的。定义是空白树（没有点和边的图）。对以下两点进行讨论：

(1) 如果这棵树在优美树群中不可以分解的（即在加法和乘法下它不能拆分），那么的组成就是它本身。那么以其本身形成的

故每一部分是优美的。

(2) 如果这棵树在优美树群中在加法和乘法下可以分解，因为是一棵优美树，则可以把按照优美群中的加法和乘法进行分解必然可以得到

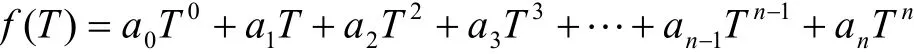
由分解方法知每个部分显然是优美的。故定理成立。

定理5如果一棵树能被“一刀切”，那么这棵树是优美的。

证明如果一棵树存在完全割边或者完全割点，对其边进行切割或者对其割点进行切割，就会形成两个部分，每个部分的直径都是一样的且每一部分的直径比切割之前树的直径要小。如果这样的树能够一直切割下去最终得到每一部分的直径小于等于 5，则称原始的树（即未切割之前的树）是优美的。现分四种情况给出其证明。

情况⑴原始树T仅存在完全割边。在这里我们规定每切割一次形成的子树（两部分是完全一样的）记为1T，切割k次，形成的子树记为。当进行k次切割过后，形成子树为且其直径小于等于5，则称树T是优美的。因为进行次切割过后，树T被分成了个完全相同的部分，因为是优美的[3]，由定理1知是优美的，又，则是优美的。则依次类推出是优美的，又，则T是优美的。

情况⑵原始树T仅存在完全割点。原始树T进行k次切割过后，树T被分成了个完全相同的部分Tk，若Tk的直径小于等于 5[3]，则称树T是优美的。由定理2知是优美的，又，则是优美的。则依次类推出优美的，又，则T是优美的。

情况⑶原始树T不可能同时存在完全割边和完全割点。因为树的顶点数与边数的关系为n=m+1，其中n为树的顶点数，m为树的边数。n,m互为奇偶的，故不可能同时存在完全割点和完全割边。

情况⑷原始树T第一次切割时存在完全割边（完全割点），切割依次过后存在完全割点（完全割边），进行k次切割过后，形成子树为Tk且其直径小于等于5，则称树T是优美的。由定理1和定理2及以上情况⑴，情况⑵知这种情况是成立的。

综上所述，为判断一些树是优美树给出了判断方法。

[1]Burzio M, Ferrarese G. The subdivision graph of a graceful tree is a graceful tree[J]. Discrete mathematics,1998, 181(1-3): 275-281.

[2]Aldred R E L, McKay B D. Graceful and harmonious labellings of trees[J]. Bull. Inst. Combin. Appl, 1998, 23:69-72.

[3]Hrnčiar P, Haviar A. All trees of diameter five are graceful[J]. Discrete Mathematics, 2001, 233(1-3):133-150.

[4]ZHAO S H I L I N. All trees of diameter four are graceful[J]. Annals of the New York Academy of Sciences, 1989, 576(1): 700-706.

[5]Huang C, Rosa A. Decomposition of complete graphs into trees[J].Ars Combinatoria,1978（5）:23-63

[6]Bloom G S. A Chronology of the Ringel-kotzig Conjecture and the Continuing Quest to Call All Trees Graceful[J].Annals of the New York Academy of Sciences, 1979, 328(1): 32-51.

[7]Body J A , Murty u. Graph Theory with Application[M].New York:Elsevier,1976.

[8]Huang C. Further results on trees labellings[J].Utilitas Math.,1982;21C:31-48

[9]张先迪 ,李正良.图论及其应用[M]. 北京:高等教育出版社,2005.

[10]喻卫,刘二根. 一类树 Tk1⊕k3的优美性[J].宜春学院学报,2013,35(6）:10-11,67.

[11]丁宗鹏, 喻卫, 徐保根. 关于图的符号路 (点) 控制[J].宜春学院学报, 2012, 34(4): 4-6.