Taylor 中值定理余项的统一及证明

杜争光

（陇南师范高等专科学校数学系，甘肃，成县 742500）

1 引言及主要引理

文献[1]对 Taylor公式“中点函数”的可微性进行了研究，在附加了单调的条件下，证明了“中点函数”的可微性，并得到了该函数在a的导数公式，推广了渐进性的相关结论；文献[2]进一步推广了这一结果，讨论了广义Taylor中值定理“中点函数”的性质，得到了更加一般的一个结；文献[3]将微分中值定理和积分中值定理统一在一个表达式中，并对已有成果进行了推广；文献[4]讨论了推广之后的微积分中值定理“中间点”的渐进性，得到了一个一般性的结论。

本文将继续对Taylor中值定理进行推广，得到了一个更具一般性的余项形式，对Taylor中值定理的 Peano余项、Lagrange余项、Cauchy余项、Schlomilch-Roche余项、积分型余项和广义积分型余项等六个余项进行了统一表述。讨论了该余项“中间点”的渐进性，推广了已有的一些结论，可作为文献[1-4]的补充和完善。文中需要几个重要引理，现引述如下：

引理1[5]若函数f(x)在a的某邻域内存在n＋1阶导数，且存在实数α≥0，对∀x∈有

引理2若函数φ(x)在a的某邻域内连续，且存在实数，对∀x∈有

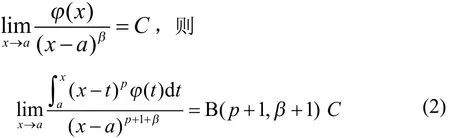
其中，=是Beta函数。

引理3[3]若函数在闭区间上存在n+1阶导数，函数在闭区间上存在阶导数，且，，则至少存在一点，使得

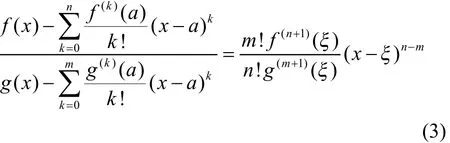
2 主要结果

定理1若函数在a的某邻域内存在n＋1阶导数，函数在内连续，则对于，，至少存在一点在a与x之间，有

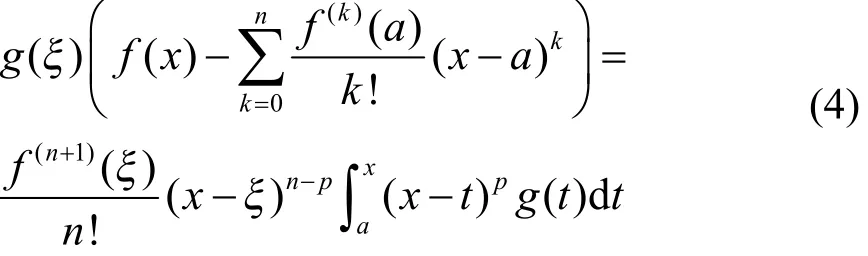
证明 对于，(不妨设x＞a，对于x＜a的情形同理可证)，构造函数

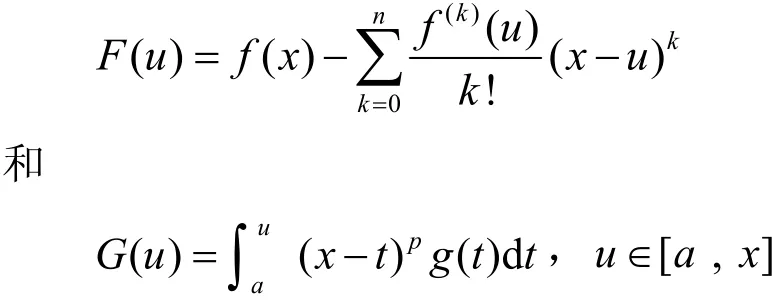
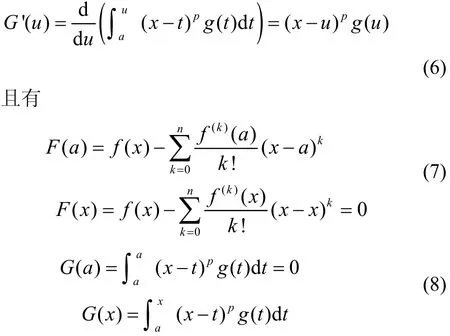
现考查函数，

(i) 在闭区间上连续；

(ii) 在开区间内可导；

(iii)

由 Rolle定理，存在一点，使得，而

综合(5)-(9)，便有

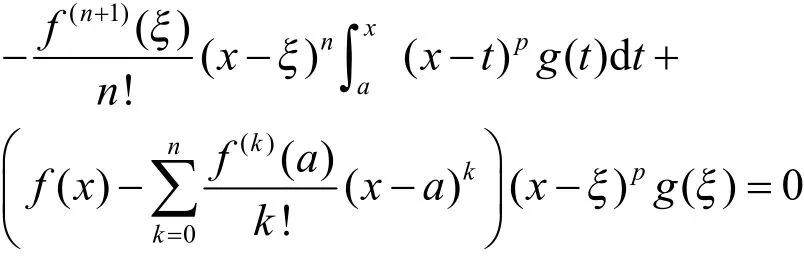
整理上式，并注意到，便有

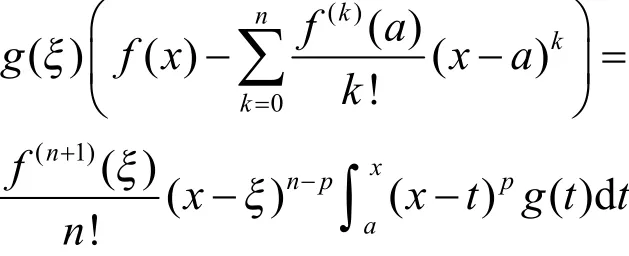
注在定理 1中，当时，积分是定积分，结论成立。而当时，积分是反常积分，且以t=x为瑕点的瑕积分，而由于在内连续和p∈(-1 , 0)，容易证明反常积分是收敛的，结论仍然成立。后续的定理中存在同样的问题，不再赘述。

以上证明过程中，没有考虑的非零性，即当有零点时，不影响结论的正确性。若时有时，便有如下结论。

定理2若函数在a的某邻域内存在阶导数，函数在内连续，且，，则对于，，至少存在一点在a与x之间，有

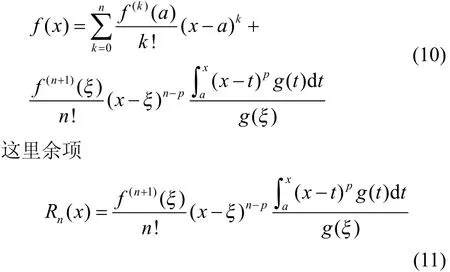
这是一个更具有一般性的余项形式，这里是实数，且有以下特殊形式：

1. 当≡ 1 时，，包含了以下四种余项形式：

1) 当p=n时，是Lagrange余项；

2)当p=n时，o((x-a)n)，这是Peano余项；

3)当p= 0 时，这是Cauchy余项；

4) 当p=q- 1时，，这是Schlomilch-Roche余项，此时。

2.当时，

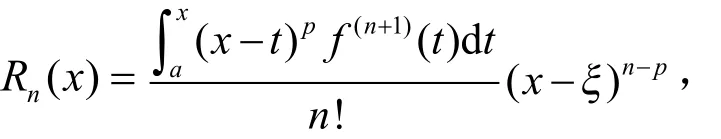
这是一个积分型余项的推广形式，当p=n时，

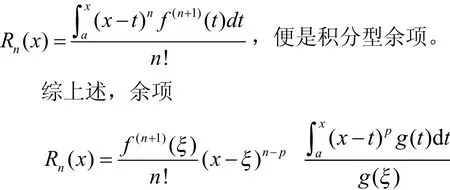
是Taylor中值定理余项的一个推广，它涵盖了Taylor中值定理所有余项的一般余项形式。

下面讨论，由公式(11)中余项所确定的“中间点”的渐进性。

定理3若函数在a的某邻域内存在n＋1阶导数，函数在内连续，，，且存在实数，，对

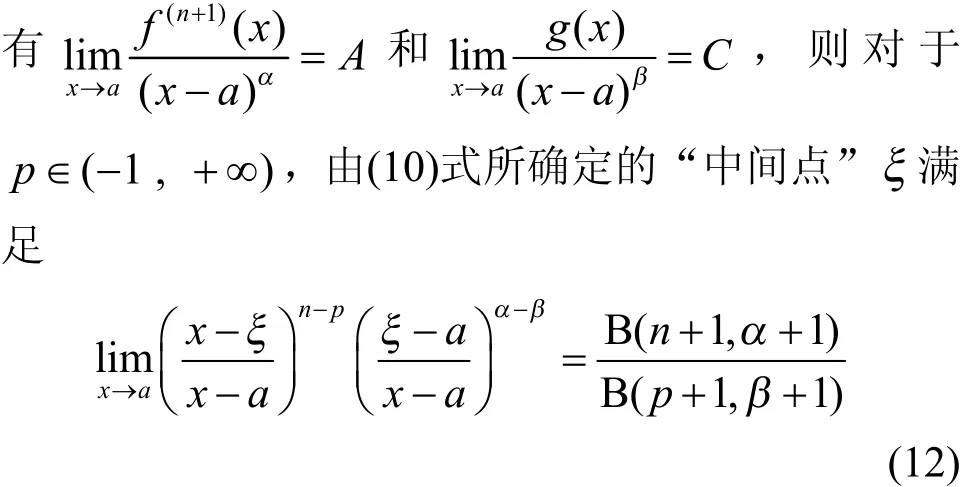
证明由于函数在内存在阶导数，对于实数α≥0和，构造函数

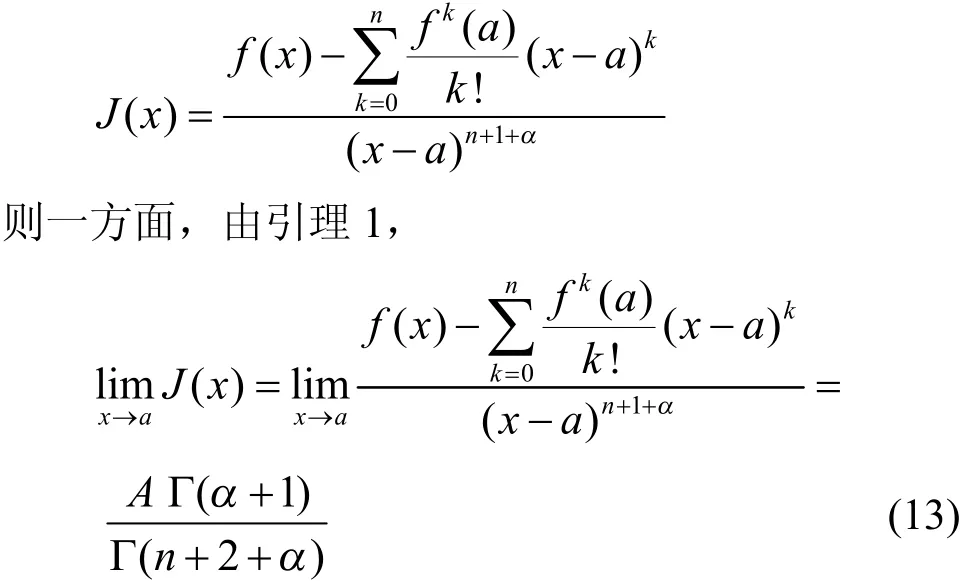
另一方面，由定理1和引理2（注意到时

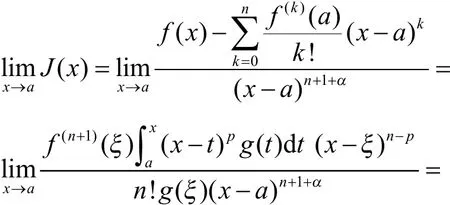
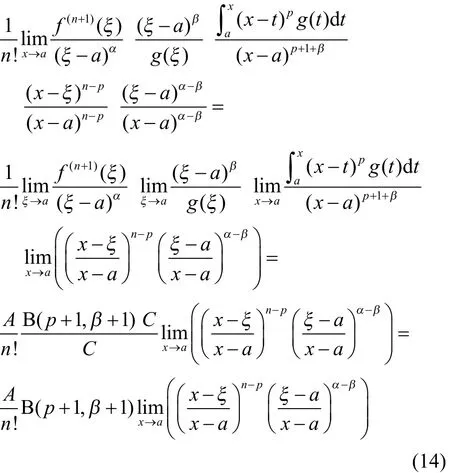
综合式（13）和式(14)，有

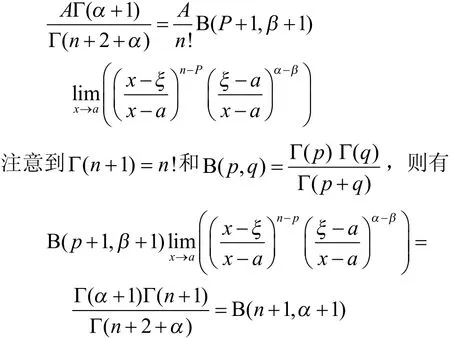
所以，

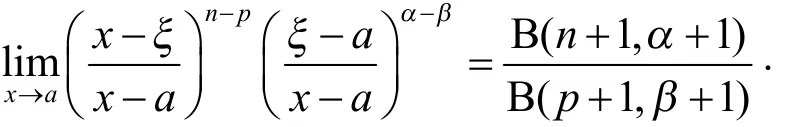
这一渐进性的结果比文献[1-5]的结果更具有一般性和广泛性。

当p=m∈N时，有以下推论：

推论若函数在a的某邻域内存在阶导数，函数在内连续，，，且存在实数α≥0，β≥0，对∀x∈有则对于且m≤n，由引理3的(3)式所确定的“中间点”ξ满足

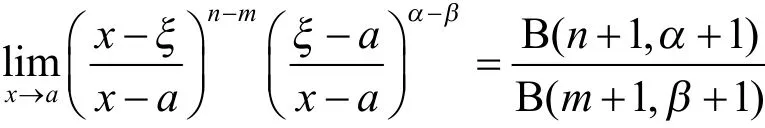
这一结果与文献[5]的定理1一致，这也表明(12)更具有一般性。

另外，当定理 3中的参数n，p，α，β取不同的值时都会有一些特殊形式的结果，这里不再叙述，可以参考文献[1-8]。

[1]李丹,张树义.关于泰勒公式中间点函数的可微性[J].井冈山大学学报: 自然科学版,2016,37(6):11-14.

[2]赵美娜,张树义,郑晓迪. 广义 Taylor 中值定理 “中间点函数” 的性质[J]. 南通大学学报:自然科学版, 2016,15(3):80-85.

[3]杜争光.微积分中值定理的统一及推广[J].荆楚理工学院学报,2011,26(2):34-37.

[4]杜争光.微积分中值定理“中间点”的渐进性的统一[J].湖南工程学院学报:自然科学版,2012,22(3):60-62.

[5]杜争光.广义Cauchy中值定理“中间点”的渐进性[J].数学的实践与认识,2015,45(13):268-272.

[6]赵美娜,张树义,郑晓迪.泰勒公式“中间点函数”的一个注记[J].鲁东大学学报:自然科学版,2016,32(4):302-306.

[7]布仁白乙拉,苏雅拉图.某些含有Dini导数的微分中值定理“中间点”的渐近性[J].井冈山大学学报:自然科学版,2017,38(2):25-29.

[8]刘冬红,张树义,郑晓迪.二元函数柯西中值定理“中间点”的渐近估计式[J].井冈山大学学报:自然科学版,2017,38(4):13-17.