列车荷载下钢轨振动加速度的空间分布特征
2018-06-01蔡小培郭亮武钟阳龙
蔡小培, 谭 希, 郭亮武, 钟阳龙
(北京交通大学土木建筑工程学院, 北京 100044)
钢轨是包含轨头、轨腰和轨底的空间结构,具有引导车辆前进、承受和传递车轮荷载的功能[1].轮轨动态冲击下,钢轨产生剧烈振动,并会向扣件、轨枕、道床及基础传递.钢轨振动在轨道结构中最为显著[2-3],对分析轮轨关系、轨道损伤、振动传播、制定评价指标等方面有重要意义.钢轨振动的剧烈程度,可以采用钢轨振动加速度进行衡量[4].研究钢轨振动加速度在其横截面和沿线路纵向的分布特征,确定钢轨振动的敏感区域和测量参数,对于评价轮轨间冲击振动具有重要的科学价值和工程意义.
钢轨加速度是铁路动力试验的主要测量指标,可用于评价轨道的振动特性或轮轨冲击效应[5-7].Remington[8]在两个轨枕之间的钢轨上安装了6个加速度传感器,测量钢轨加速度以预测轮轨噪声.刘林芽等[9]在轨枕之间的钢轨轨腰设置加速度计,测定钢轨加速度,评定提速线路路桥过渡段动力响应.马春生等[3]在普通道床和弹性道床轨枕之间的钢轨轨底位置安装了加速度计测试钢轨加速度,分析桥上弹性轨枕有砟道床减振、隔振力学特性.
既有车辆-轨道动力分析中,钢轨往往模拟为连续或离散支承的Euler梁或Timoshenko梁[10-12].Euler梁仅考虑钢轨弯曲变形,不考虑剪切变形,简化了动力计算.Timoshenko梁考虑钢轨剪切变形和转动惯量,相比于前者力学分析更加准确,但计算过程相对复杂.随着车辆-轨道动力学的发展,车辆和轨道模型更为精细,但是钢轨的模拟仍很简单,只能够计算单点振动加速度.然而,钢轨不同位置的加速度会不同,如果不考虑这一因素,会影响数值计算和动力试验的可靠性和准确度.因此,开展钢轨加速度空间分布特征的研究,十分重要.
本文建立车辆-轨道耦合动力学模型和轨道-下部结构有限元模型,研究分析不同轨道结构、轨道不平顺和列车速度对钢轨振动特性的影响,为确定钢轨振动敏感区域、加速度传感器参数提供指导.
1 计算模型的建立
1.1 车辆-轨道动力模型
GENSYS是模拟轨道车辆运行的三维多体动力学程序,广泛应用于分析车辆动力行为,能够计算车辆振动、轮轨力和轮轨接触斑等[13].本文基于GENSYS建立车辆-轨道耦合动力学模型,包括车辆模型、轨道模型和轮轨接触模型,如图1所示.
整车模型是由车体、转向架、轮对组成的多体系统,车体、转向架、轮对设置为刚体,通过弹簧-阻尼单元模拟的悬挂系统进行连接.模型具有38个自由度,其中车体、转向架各有6个自由度,分别是横向、垂向、纵向、侧滚、摇头和点头;轮对则考虑5个自由度,分别是横向、垂向、侧滚、摇头及点头.车体与转向架之间采用赋予了二级悬挂参数的弹簧阻尼单元连接,转向架与轮对之间采用赋予了一级悬挂参数的弹簧阻尼单元进行连接.轨道模型设置为连续弹性支承模型,钢轨采用Euler梁模拟.钢轨和轨道板通过扣件连接,由弹簧和粘性阻尼器模拟.
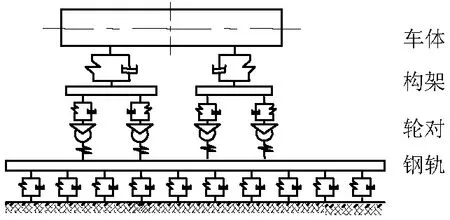
图1 车辆-轨道耦合动力学模型Fig.1 Vehicle-track coupling dynamics model
轮轨接触关系包括正向相互作用和切向相互作用.采用Hertz非线性弹性接触理论计算法向接触力,车轮和钢轨之间相互挤压产生法向力p(t),车轮和钢轨分开时p(t)=0.法向力定义[3]为
(1)
式中:G为轮轨接触常数;ΔZ(t)为轮轨接触斑上的法向弹性压缩量;t为时间.
分析切向相互作用时考虑轮轨蠕变比,在蠕滑力的计算中,首先基于Kalker蠕滑理论FASTSIM进行计算,然后采用沈氏理论进行修正.蠕变力是包括纵向和横向力的非线性力.
由动力学模型可计算不同车辆、不同轨道不平顺状态下的轮轨垂向力.车辆轴重22 t、时速160 km/h,线路为传统有砟轨道,不平顺激扰为我国既有线轨道垂向不平顺[14].考虑无轨道不平顺和有轨道不平顺两种线路状态分别进行计算,轮轨垂向力结果见图2所示.将计算得到的轮轨力数据导入有限元模型进行计算,分析钢轨振动加速度.
1.2 轨道-下部结构动力模型
就有砟轨道而言,轨道-下部结构有限元模型包括钢轨、扣件、轨枕、道床和路基部件,其中采用弹簧阻尼元件模拟扣件,其余部分均采用可变形的实体单元模拟.钢轨采用我国CN60截面,综合考虑计算机性能、精度,轨头表面单元长、宽尺寸分别为0.010、0.005 m.考虑扣件垫板的均匀支承,扣件横向、纵向分别设置3个弹簧阻尼元件,垂向刚度为7.5×107N/m,横向刚度为3.9×107N/m.混凝土轨枕尺寸为2.6 m×0.2 m×0.3 m,间距为0.6 m;有砟道床由C3D8R实体单元来模拟,厚度为0.3 m.轨道-下部结构有限元模型如图3所示.
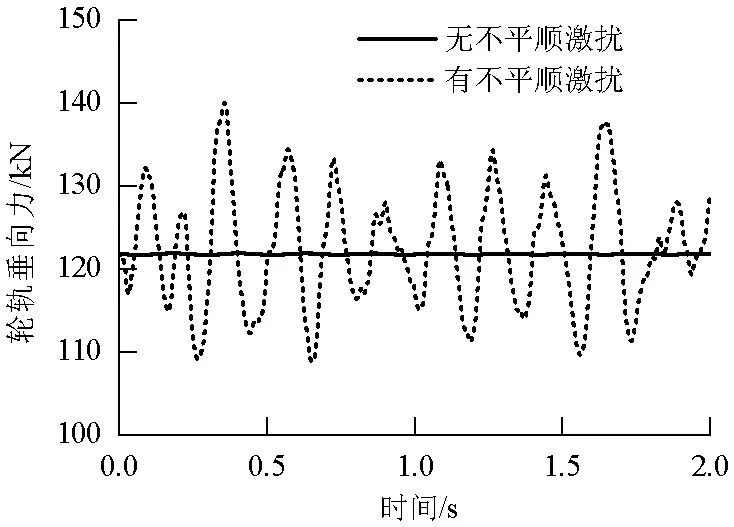
图2 轮轨垂向力图示Fig.2 Wheel-rail vertical force

图3 轨道-下部结构有限元模型Fig.3 Track-substructure FE model
无砟轨道用整体混凝土轨道板代替了传统的轨枕和有砟道床.轨道板采用C40混凝土,支承层采用C15混凝土,均采用实体单元模拟.无砟轨道扣件间距为0.6 m,垂向刚度为5.0×107N/m,横向刚度取为3.9×107N/m.轨道振动在一定程度上受地基结构的影响,因此在模型中考虑路基结构的振动.路基模型高度是3 m,边坡斜率为 1∶1.75,为了消除轨道边界条件的影响,整体模型长度取为100 m,钢轨加速度测量点位于模型中部.此外,为了防止振动反向传递,在模型的每一侧设置弹簧阻尼元件作为吸收边界.
1.3 轮轨力传递方式
车辆与轨道的动力相互作用通过轮轨接触传递.钢轨和轮对是弹性模量较大的弹性体,根据Hertz接触理论,轮轨接触斑是椭圆形,位于轨头上表面.基于车辆-轨道模型中得到的轮轨接触斑,在有限元模型中建立轮轨接触斑模型,如图4所示.
在轮轨力加载过程中,以接触斑作为移动加载平台,轮对速度通过边界条件的方式施加于加载平台,忽略椭圆形接触斑中应力分布不均匀现象.列车在直线段行驶时,根据车辆-轨道耦合动力学模型的计算结果,椭圆形接触斑长轴、短轴尺寸分别取为16、8 mm,忽略轨头表面接触斑的横向位移.

图4 椭圆形轮轨接触斑Fig.4 Ellipse point of the wheel-rail contact
将多体动力模型中计算得到的轮轨力作为有限元模型的激励源,导入到有限元模型中模拟实际轮轨力随时间的变化.基于ABAQUS预处理环境,将轮轨力作用于有限元模型中的椭圆加载平台,并随之移动.此外,轮轨横向力大约为2~3 kN,与垂向力相比小很多,所以横向力的影响可以忽略不计,也不会对最后的分析结果造成较大的影响.
1.4 钢轨测点布置
分析计算时,考虑钢轨加速度的空间分布特征,沿轨道纵向选择两个截面,一个位于轨枕上方,另一个位于轨枕之间.每个截面包含12个加速度值测点,分别位于轨头、轨腰和轨底;钢轨内、外侧加速度测量点是对称的,每侧各有6个测量点.轨头的两个测量点位于距轨头踏面下16 mm和25 mm处,轨腰的两个测量点位于轨腰上侧和中性轴处,轨底的两个测量点位于在底面上表面的中心和边缘处.钢轨截面加速度测点布置如图5所示.
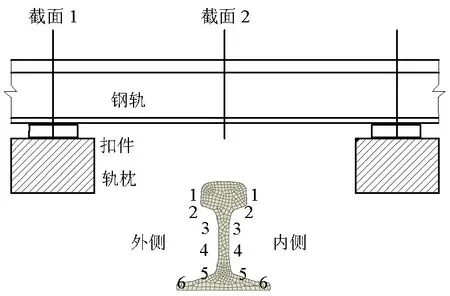
图5 钢轨加速度测点布置Fig.5 Distribution of test points for rail acceleration
2 计算结果分析
有砟轨道占世界铁路的90%.对于有砟轨道,钢轨和混凝土轨枕通过扣件连接形成轨排结构,沿轨道纵向扣件对钢轨为点支承.无砟轨道系统中,钢筋混凝土作为基本结构代替传统颗粒状有砟轨道,线路平顺性、稳定性好,列车速度也大幅度提升.支承方式不同导致钢轨的约束和传递特性不同.另外,同一钢轨截面上轨头、轨腰和轨底与轮轨激励源的距离也不同,不同位置的钢轨振动有差异.
2.1 加速度分布规律
车辆以速度160 km/h运行在无不平顺激扰的有砟轨道线路时,钢轨加速度时程曲线如图6所示.当车辆动力荷载接近测试断面时,钢轨加速度持续增加;当车辆荷载位于测试断面正上方时,加速度达到最大值;当载荷逐渐远离测试断面时,振动加速度不断衰减,逐渐减小到0.轮轨碰撞作用于轨头,振动瞬间传递到轨腰和轨底.由于振动在传递中的衰减、扣件约束以及钢轨的阻尼特性等因素,钢轨加速度从轨头到轨腰逐渐衰减,轨头振动加速度振动幅值大于轨腰、轨底加速度振动幅值.
图7为有砟轨道钢轨加速度.由图7(a)可以看出,钢轨内、外侧相同位置处的加速度几乎相同.
由于轮轨碰撞直接作用于轨头,所以轨头的加速度最大,轨腰、轨底的加速度相对较小.对于轨枕上方的测试断面,由于轨下垫板的约束和弹条的局部屈曲效应,轨底中部、边缘两处测点的钢轨加速度峰值较接近.

图6 钢轨垂向加速度振动响应Fig.6 Vibration response of vertical rail acceleration

(a) 轨枕上方(b) 轨枕之间图7 有砟轨道钢轨加速度Fig.7 Rail acceleration of ballasted track
轨枕之间的钢轨加速度如图7(b)所示,轨头加速度明显大于轨腰、轨底位置,但小于轨枕上方的轨头加速度.轨腰部分所有测点的振动加速度都十分接近,轨枕之间测点的轨底振动加速度略大于轨枕上方测点的轨底加速度.因为轨枕之间的轨底没有约束,所以轨底边缘6号测点的加速度远大于轨底中部5号测点.以上现象的产生是由于扣件对轨底约束的影响.考虑到钢轨内、外侧加速度的一致性和传感器现场安装的实用性,以下仅对钢轨外侧的振动加速度进行计算分析.
2.2 列车速度的影响
基于车辆-轨道动力模型,不考虑轨道不平顺,得到了车速v=100,120,160 km/h时的轮轨垂向力.随着列车速度提高,轮轨间冲击强度加剧,轮轨力随之增大.随着载荷移动速度的增加,轮轨冲击加剧,钢轨测试断面的加速度增大,其中轨头加速度变化最为明显,结果如图8所示.随着车速增大,钢轨轨头加速度与轨腰、轨底相比增长幅度变大,轨头振动对速度变化更为敏感.3种速度下轨枕上方测点的钢轨加速度大于轨枕之间测点.
2.3 轨道不平顺的影响
轨道不平顺是轮轨碰撞振动的主要激励源,轨道垂向不平顺对轮轨垂向力有着重要影响,如图2所示.考虑轨道不平顺后轮轨垂向力显著增加,峰值从122 kN增加至140 kN.然后将轮轨力导入轨道-下部结构有限元模型进行下一步计算,分析轨道不平顺作用下的钢轨加速度变化规律.轨头、轨腰和轨底加速度变化见图9.由图9可以看出,与轨腰和轨底的加速度相比,轨头的加速度相对较大.轨枕上方钢轨的加速度对轨道不平顺更加敏感.轨枕上方的加速度测点中,考虑轨道不平顺时轨头加速度明显增大,轨腰和轨底的加速度几乎没有变化.轨枕之间轨头加速度测点的计算结果没有表现出明显的规律.

(a) 轨枕上方(b) 轨枕之间图8 不同速度下钢轨加速度Fig.8 Rail acceleration for different velocities
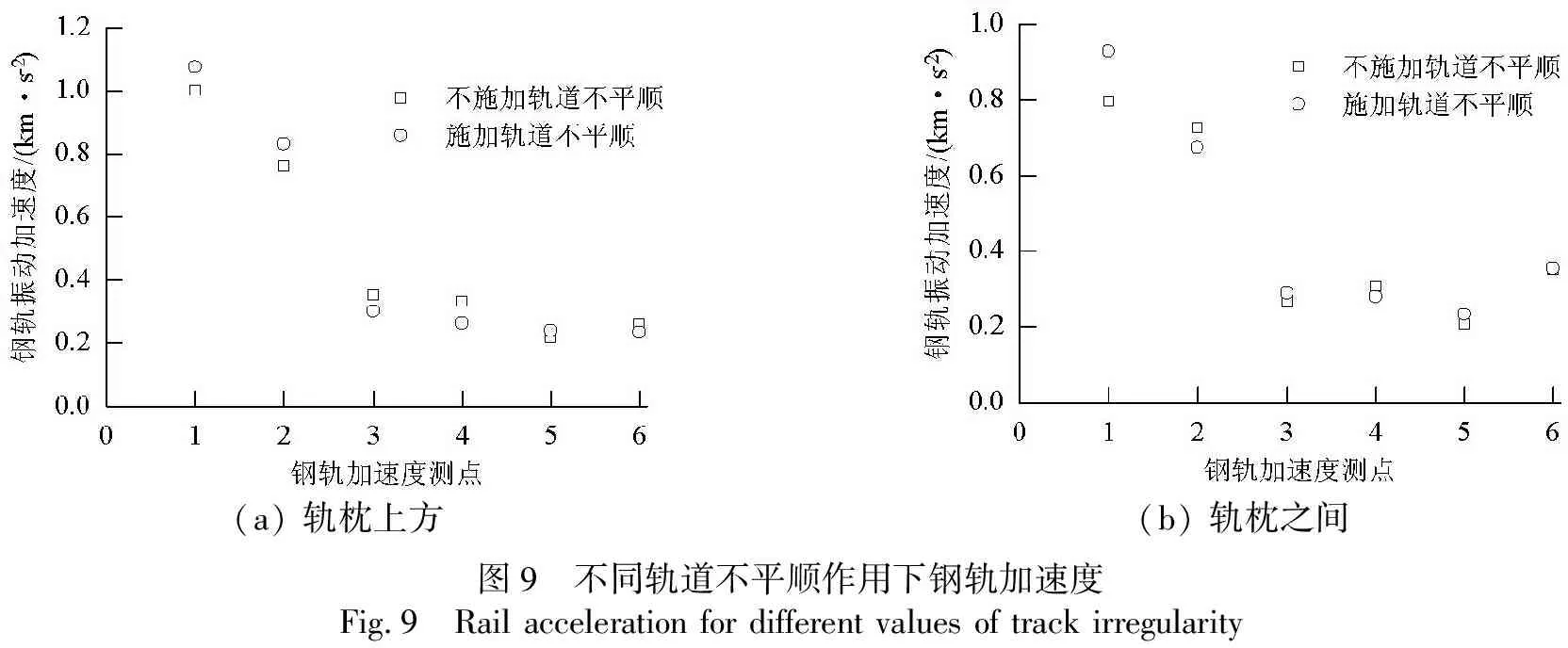
(a) 轨枕上方(b) 轨枕之间图9 不同轨道不平顺作用下钢轨加速度Fig.9 Rail acceleration for different values of track irregularity
总体而言,轨道不平顺导致轮轨冲击振动更加明显,钢轨加速度显著增加.在铁路运营中,轨道不平顺更为复杂,此外还需考虑车轮踏面缺陷等问题,以上因素都将导致轨道加速度进一步增大.由计算结果可知,复杂运营条件下有砟轨道钢轨加速度可达到1.0 km/s2,甚至更大.因此,监测有砟轨道钢轨加速度时,建议传感器的量程范围应该在1.0~2.0 km/s2.
2.4 轮轨接触斑偏移的影响
铁路运营中车辆常出现蛇行运动现象,轮轨接触斑会横向偏移,这可能会导致钢轨加速度分布发生很大变化.为了研究轮轨接触斑偏移产生的影响,有限元模型中的接触斑分别为向轨道内侧、外侧偏移10 mm.轨枕之间钢轨区段轮轨冲击减弱,钢轨加速度分布规律如图10所示.结果表明,轮轨接触斑偏移会影响钢轨加速度,靠近加载平台一侧测点的钢轨加速度大于另一侧测点的加速度.
2.5 支承方式的影响
无砟轨道在我国高速铁路广泛应用.本节主要分析不同支承方式对钢轨加速度的影响,考虑传统的离散支承式无砟轨道和连续支承式无砟轨道结构.以CRH3为例,轴重为15 t,当列车以350 km/h通过离散支承式无砟轨道,轨枕上方和轨枕之间两个截面的钢轨加速度峰值如表1所示.

图10 内外侧测点的钢轨加速度差异Fig.10 Difference in rail accelerations between the outer and inner points
分析两个截面的数据,可以发现轨头加速度明显大于轨腰和轨底的加速度.这主要是由于轮轨碰撞作用于轨头,振动在从上到下传动过程中逐渐衰减.此外,轨枕上方钢轨的加速度大于轨枕之间钢轨的加速度.轨头、轨腰、轨底的加速度如图11所示.列车速度为200、300、350 km/h,轨枕上方轨头加速度分别为1.4、2.3、2.9 km/s2,轨枕之间轨头加速度分别为1.3、1.9、2.2 km/s2.随着列车速度提高,轨枕之间和轨枕上方钢轨各个位置的加速度均不断增加,轨头、轨腰、轨底加速度变化速度不同,基本呈非线性增长趋势.
表1无砟轨道钢轨垂向加速度
Tab.1 Vertical rail acceleration of slab track m·s-2

外侧测点测面1测面212 9802 26021 9682 0343500510460460054705926397729
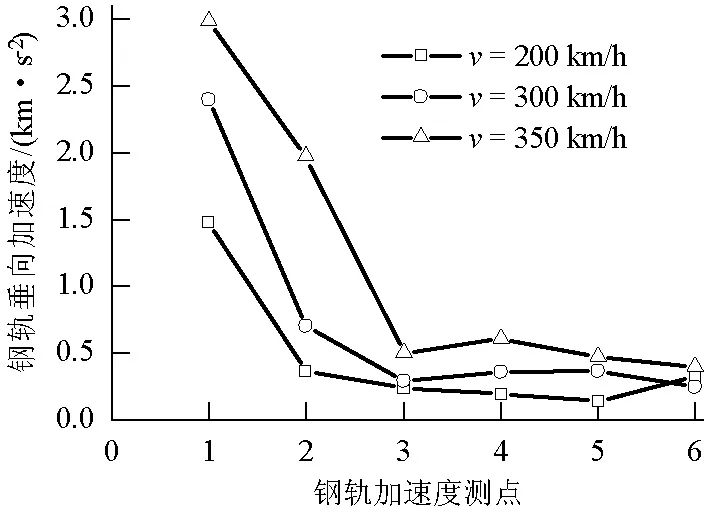
(a) 轨枕上方
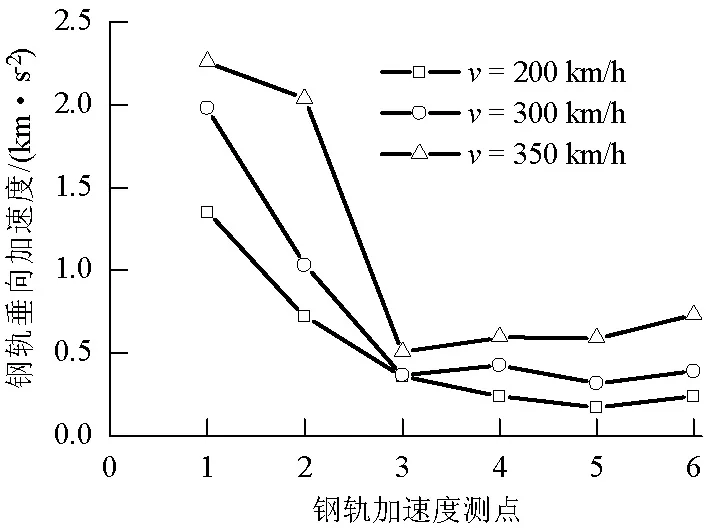
(b) 轨枕之间图11 不同速度下钢轨加速度Fig.11 Rail acceleration for different velocities
以轴重22 t、速度160 km/h的车辆为基本参数,对比分析有砟轨道和无砟轨道的钢轨振动特性.分析轨枕上方钢轨截面1的计算结果,有砟轨道和无砟轨道钢轨加速度如图12所示.可以看出,在相同的计算条件下,无砟轨道的钢轨加速度小于有砟轨道的钢轨加速度.
连续支承式无砟轨道的扣件支承和轨下结构都是连续的,一般适用于有轨电车等线路[15],其钢轨受力更为均匀、连续[16].本文考虑在高速铁路上采用连续支承无砟轨道,并对其振动特性进行计算.连续支承、离散支承无砟轨道结构模型中,线路单位长度范围内扣件刚度相同.列车以350 km/h运行时,钢轨加速度如图13所示.
由图13(a)可以看出,连续支承无砟轨道的钢轨振动衰减较快,主要是因为连续支承条件下扣件底部约束的影响更强;连续支承无砟轨道轨头加速度振动幅值大于轨腰、轨底加速度振动幅值.由图13(b)可以看出,连续支承无砟轨道钢轨在4 kHz附近出现较大振动响应峰值.
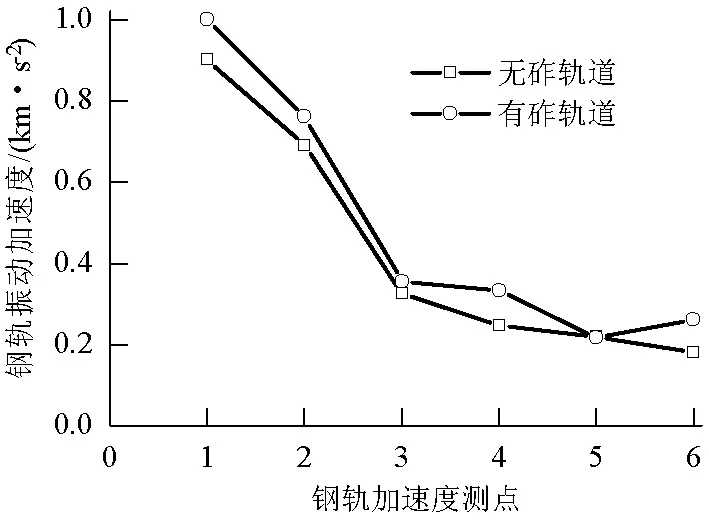
图12 截面1钢轨加速度(v=160 km/h)Fig.12 Rail acceleration of section 1 (v=160 km/h)
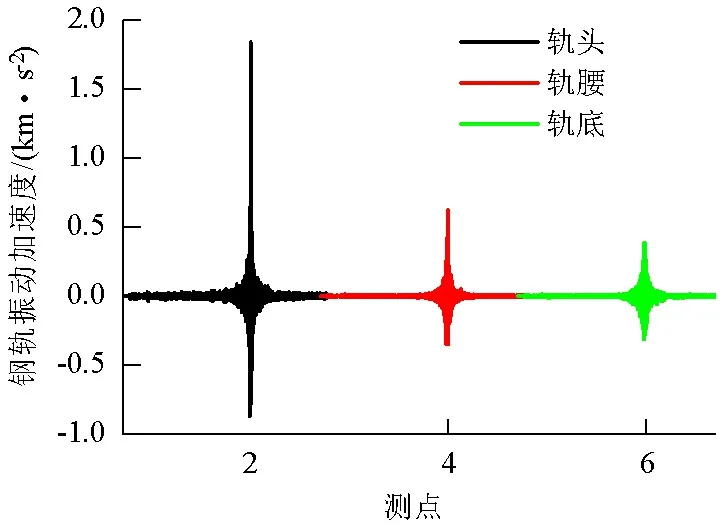
(a) 加速度时程曲线

(b) 轨头加速度频谱图13 连续支承无砟轨道钢轨垂向加速度Fig.13 Vertical rail acceleration in continuously supported track structure
由图14可知,离散支承无砟轨道与连续支承无砟轨道相比,钢轨加速度相对较大,这是因为在离散支承无砟轨道轨下支承刚度不均匀,两支承点间钢轨结构自由,导致钢轨振动加速度较大.当连续支承无砟轨道结构轨下基础刚度增加时,轨头、轨腰、轨底的振动加速度也会随之增加.
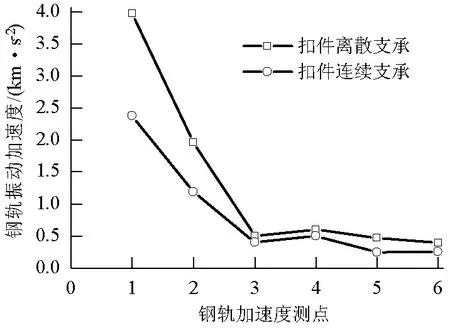
图14 不同支承类型下钢轨加速度Fig.14 Rail acceleration for different types of rail supports
综上所述,列车荷载下,轨头振动最敏感,也是钢轨加速度最大的区域,轨头加速度远远大于轨腰和轨底.高速铁路无砟轨道上进行钢轨加速度试验时,建议传感器布置于轨头,量程应达3.0 km/s2,频域量程应达4 kHz以上;对于特殊结构和振动冲击较大区域,如伸缩调节器、道岔尖轨与心轨等,推荐使用量程达到5.0 km/s2的加速度传感器.
3 现场测试验证
为验证钢轨振动加速度传递规律的理论计算结果,在北京交通大学轨道工程实验室进行了钢轨加速度锤击试验,并在朔-黄铁路进行了现场测试.
3.1 实验室锤击试验
图15为现场锤击试验及数据.采用力锤进行锤击;钢轨振动加速度测试采用CA-YD-181的压电加速度传感器,灵敏度为1.0 mV/m·s2,量程为±500g;数据采集系统采用德国IMC(integrated measurement & control)集成测控有限公司生产的便携式数据采集系统.所测得的轨头、轨腰、轨底加速度值分别为168g、87g、53g.根据钢轨锤击试验结果可知,钢轨加速度从轨头到轨腰到轨底逐渐减小,加速度在钢轨空间分布规律与仿真模型计算规律基本相符.
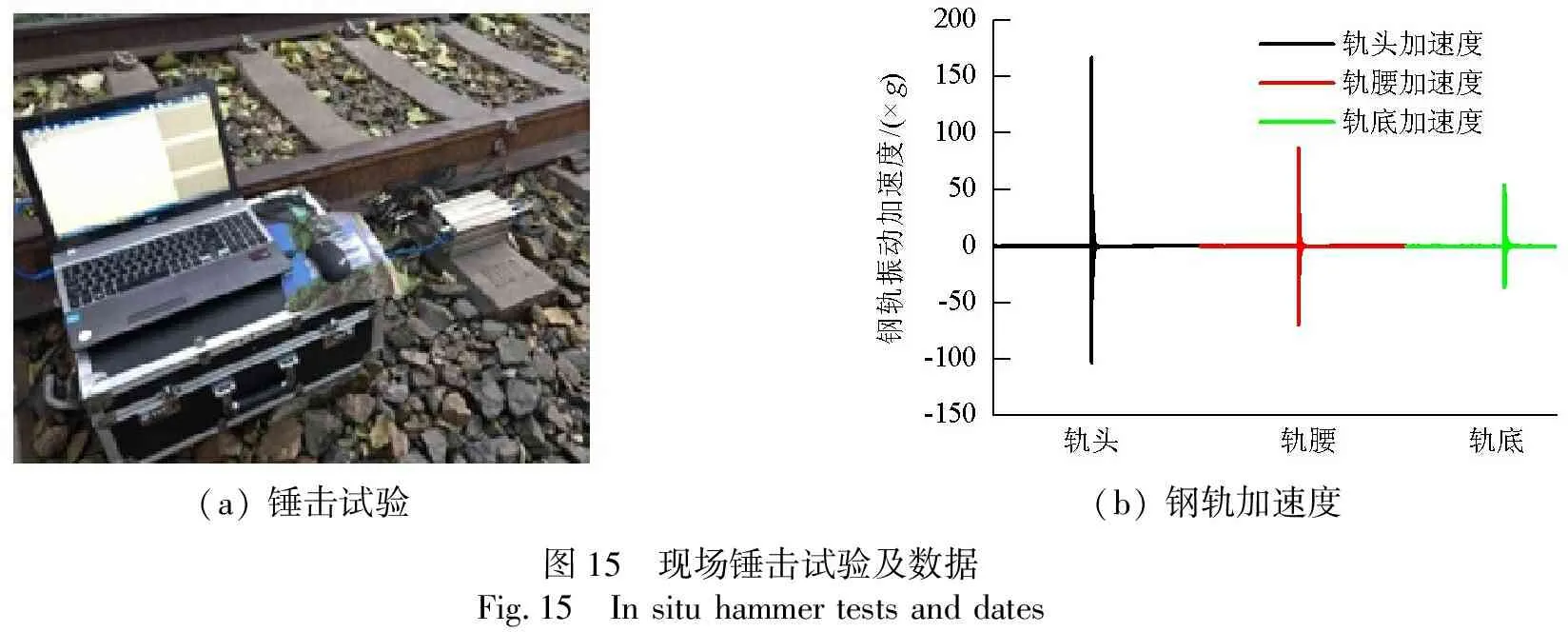
(a) 锤击试验(b) 钢轨加速度图15 现场锤击试验及数据Fig.15 In situ hammer tests and dates
3.2 重载铁路现场测试
在朔-黄铁路上行线进行钢轨加速度现场动态测试.列车速度为65.2 km/h,机车轴重25 t,铺设钢轨为60 kg/m,该路段钢轨更换不足4个月,钢轨平顺性较好.现场测试时加速度计安装位置按照1.4节钢轨测点布置,轨头、轨腰、轨底加速度测点分别对应图5中2、4、6测点,加速度计布置及测试数据如图16所示.由图可知,现场测得的轨头加速度为43g,轨底和轨腰加速度较为接近,分别为31g和29g,与模型计算结果图8(b)吻合度较好.

(a) 现场试验(b) 钢轨加速度图16 朔-黄铁路现场加速度测试Fig.16 In situ acceleration test for Shuo-huang railway
4 结 论
(1) 轮轨冲击直接作用于钢轨轨头,轨头加速度大于轨腰和轨底加速度.随着车速的增加和轨道不平顺的发展,轮轨碰撞急剧增强,钢轨加速度会明显增大.(2) 由于扣件系统的弹性阻尼特性,轨枕上方轨头加速度明显大于轨枕之间的轨头加速度;两个位置轨腰加速度较为接近.由于轨底约束的影响,轨枕上方轨底内外侧加速度基本相同,而轨枕之间轨底外侧的加速度大于轨底内侧的加速度.(3) 支承方式对钢轨加速度有明显影响,连续支承式无砟轨道钢轨加速度小于离散支承式无砟轨道钢轨加速度.(4) 钢轨加速度传感器建议安装在轨头外侧,因为轨头位置加速度值比其他位置的加速度值更加敏感.而且,列车运行速度越快,加速度传感器的频率、量程也应该随之增加.
[1] COENRAAD E. 现代铁路轨道[M]. 2版.王平,陈嵘,井国庆,译. 北京:中国铁道出版社,2014: 204-205.
[2] 李克飞,刘维宁,孙晓静,等. 北京地铁5号线高架线减振措施现场测试与分析[J]. 中国铁道科学,2009,30(4): 25-29.
LI Kefei, LIU Weining, SUN Xiaojing, et al. In-situ test and analysis on the vibration mitigation measures of the elevated line in Beijing Metro Line 5[J]. China Railway Science, 2009, 30(4): 25-29.
[3] 马春生,肖宏,高亮. 高速铁路弹性轨枕有砟轨道力学特性试验研究[J]. 土木工程学报,2015,48(增刊2): 81-87.
MA Chunsheng, XIAO Hong, GAO Liang. Experimental study on mechanical characteristics of elastic sleeper ballast track on high-speed railways[J]. China Civil Engineering Journal, 2015, 48(Sup. 2): 81-87.
[4] 翟婉明. 车辆-轨道耦合动力学[M]. 3版.北京:科学出版社,2007: 95-132.
[5] BARKE D, CHIU W K. Structural health monitoring in the railway industry: a review[J]. Structural Health Monitoring, 2005, 4(1): 81-93.
[6] 刘鹏辉,杨宜谦,尹京. 地铁隧道内不同轨道结构振动测试与分析[J]. 振动与冲击,2014,33(2): 31-36.
LIU Penghui, YANG Yiqian, YIN Jing. Test and analysis on vibration of different track structures in tunnel[J]. Journal of Vibration and Shock, 2014, 33(2): 31-36.
[7] LEE M L, CHIU W K. Determination of railway vertical wheel impact magnitudes: Field trials[J]. Structural Health Monitoring, 2007, 6(1): 49-65.
[8] REMINGTON P J. Wheel/rail rolling noise, Ⅱ: Validation of the theory[J]. The Journal of the Acoustical Society of America, 1987, 81(6): 1824-1832.
[9] 刘林芽,雷晓燕,练松良. 提速铁路过渡段的动力响应测试分析[J]. 铁道工程学报,2005,22(5): 15-19.
LIU Linya, LEI Xiaoyan, LIAN Songliang. Analysis of dynamic response by transition zone of speed-raise railway[J]. Journal of Railway Engineering Society, 2005, 22(5): 15-19.
[10] ZHAI Wanming, HE Zhenxing, SONG Xiaolin. Prediction of high-speed train induced ground vibration based on train-track-ground system model[J]. Earthquake Engineering and Engineering Vibration, 2010, 9(4): 545-554.
[11] 郑国琛,祁皑. 福州地铁运行引起的环境振动加速度预测分析[J]. 工程力学,2015,32(增刊1): 331-336,341.
ZHENG Guochen, QI Ai. Prediction on vibration acceleration of the environment induced by Fuzhou metro[J]. Engineering Mechanics, 2015, 32(Sup.1): 331-336,341.
[12] 翟婉明,蔡成标,王开云. 高速列车-轨道-桥梁动态相互作用原理及模型[J]. 土木工程学报,2005,38(11): 132-137.
ZHAI Wanming, CAI Chengbiao, WANG Kaiyun. Mechanism and model of high-speed train-track-bridge dynamic interaction[J]. China Civil Engineering Journal, 2005, 38(11): 132-137.
[13] PERSSONⅠ. Documentation of gensys[M]. Östersund: [s. n.], 2000: 1-18.
[14] 练松良,刘扬,杨文忠. 沪宁线轨道不平顺谱的分析[J]. 同济大学学报:自然科学版,2007,35(10): 1342-1346.
LIAN Songliang, LIU Yang, YANG Wenzhong. Analysis of track irregularity spectrum of Shanghai-Nanjing railway[J]. Journal of Tongji University : Natural Science, 2007, 35(10): 1342-1346.
[15] LIER S V. The vibro-acoustic modelling of slab track with embedded rails[J]. Journal of Sound and Vibration, 2000, 231(3): 805-817.
[16] 林红松,颜华. 有轨电车埋入式无砟轨道及关键部件型式研究[J]. 铁道工程学报,2016,33(6): 60-65.
LIN Hongsong, YAN Hua. Type research on the embedded ballastless track structures and key components of modern tram way[J]. Journal of Railway Engineering Society, 2016, 33(6): 60-65.
