振动条件下螺纹面磨损对紧固件抗松能力影响

张明远, 鲁连涛, 张远彬, 张继旺, 曾东方

(西南交通大学牵引动力国家重点实验室, 四川 成都 610031)

螺纹紧固件易拆装、可反复使用,且具有较高的联接强度，机械结构中需要反复拆装的部位多采用螺纹紧固件进行联接.但是,在振动载荷作用下,螺纹紧固件易发生松动失效.研究指出[1-4],垂直于螺杆方向的横向载荷可以在螺纹面产生大切向力,打破螺纹面原有的受力平衡,使螺纹面产生相对滑移,造成螺纹面沿松脱方向转动.在预紧力的作用下,螺纹面存在较大的法向载荷,满足磨损产生的条件[5-6].文献[7-9]中发现,振动载荷的持续作用导致螺纹面磨损的产生，螺纹面的磨损造成螺纹副配合程度的降低,紧固件预紧力的降低,使紧固件发生松动.在横向振动条件下,螺纹面磨损与紧固件松动的关系目前尚不明确.

微粒子喷丸(fine particle peening, FPP)可以强化材料表面,提高材料对磨损的抵抗[10].由于该工艺使用的丸粒尺寸小(直径50～100 μm),为普通喷丸丸粒的10%左右,不会显著改变构件尺寸,从而保证构件间正常配合.本文采用FPP工艺处理了镀锌紧固件螺纹面,比较了未喷丸紧固件(electro zinc plate，EZP)及喷丸紧固件(FPP-EZP)的抗松动能力,及螺纹面的磨损程度,从试验角度分析了螺纹面磨损对紧固件松动的影响.

文献[11]建立了考虑螺纹面磨损深度变化的螺牙结构刚度模型,该模型仅包含螺牙部分,计算了随螺纹面磨损深度的增加,各螺牙受到载荷大小的变化.在螺牙结构刚度模型基础上,本文建立了考虑整个螺栓结构的紧固件刚度模型,计算了预紧力随螺纹面磨损深度增加的变化情况，通过试验和数值计算,阐明螺纹面磨损与紧固件松动的关系.

1 试 验

1.1 试验紧固件种类

用于本研究的试验紧固件种类为:微粒子喷丸未处理及处理的镀锌紧固件.表1为两种试验紧固件的材料力学性能.

表1 试验紧固件材料力学性能Tab.1 Mechanical properties of the test fastener material

由表1可见,经微粒子喷丸处理后,镀锌紧固件的表面发生明显硬化.

微粒子喷丸处理工艺参数如表2所示,其中,300#筛号对应的丸粒平均直径为50 μm.两种试验紧固件的尺寸规格均为M5 mm×25 mm.

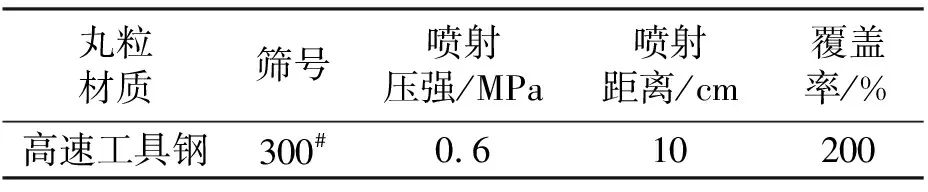
表2 喷丸处理工艺参数Tab.2 Treatment parameters of fine particle peening

1.2 试验方法

采用图1所示的紧固件横向振动试验装置进行试验.其中,基座与激振器均通过螺栓固定在T型槽中,下钢板固定在基座上.力传感器与上钢板间、加速度传感器与上钢板间均使用两液混合硬化胶固定.上、下钢板材质为45#钢,厚度均为6.5 mm,两钢板间夹滚珠减磨.

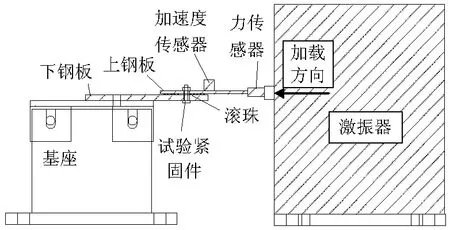
图1 紧固件横向振动试验装置示意Fig.1 Diagram of fastener transverse vibration apparatus

将施加的预紧力用式(1)换算成相应的拧紧力矩.使用数显扭力扳手拧紧试验紧固件,夹紧上下钢板.试验中,使用型号为HEV-500的激振器进行加载,激振力的大小通过型号为HEA-500G的功率放大器进行调节.通过监测上钢板的振动加速度(垂向加速度),判断试验紧固件是否发生松动失效.

T=KFd,

(1)

式中：T为拧紧力矩；K为拧紧力矩系数,取0.2[12]；F为预紧力；d为螺纹公称直径.

松动试验前,首先测试紧固件预紧力与上钢板振动加速度的关系,以便在松动试验中通过监测上钢板振动加速度判断预紧力的下降程度.对紧固件分别施加不同的预紧力,在与松动试验相同工况条件下,采集上钢板的振动加速度,得到不同预紧力对应的上钢板振动加速度.考虑试验结果的分散性,每组预紧力测试5根试样,取均值.

松动试验中,激振器加载幅值均设为激振器最大输出载荷的50%,即250 N.激振器选取恒流控制模式,以保证激振力在试验中稳定在250 N.紧固件的松动不受加载频率的影响[1],但过高的加载频率会导致功率放大器的工作功率过大,不利于设备正常使用.因此,将加载频率设置在较低的频率范围内,取20 Hz.试验以预紧力降低80%为松动准则[13],分别测试两种紧固件的松动寿命,若5×105次不松动则认为不失效.每种紧固件在进行试验时,第1根试样的预紧力取屈服极限的50%～70%,第2根试样的预紧力则根据第1根试样结果而定.若试样松动(失效),增加预紧力;反之(未失效),减小预紧力,直至得到保证紧固件不松动的最小预紧力值,即预紧力耐久极限.然后取一级较低水平的预紧力,测定在相同预紧力的条件下,两种紧固件的松动寿命.此外,紧固件拧紧后,需在螺母外表面与上钢板表面涂标记线.对发生松动失效的试样,采用力矩扳手重新将螺母拧紧至与标记线重合,记录力矩值.

1.3 试验结果

1.3.1紧固件预紧力与上钢板振动加速度关系

图2为紧固件预紧力与上钢板振动加速度的关系.由图2可见,紧固件的预紧力越高,上钢板振动加速度越小.振动加速度随着预紧力呈非线性变化,且两种紧固件的变化趋势基本一致.将两组试验数合并起来拟合得到关系式(2).根据本研究的松动准则,将初始预紧力的80%代入式(2),可得到松动失效时对应的上钢板振动加速度.

a=4.265e-0.001 306F,

(2)

式中：a为钢板振动加速度.

图2 预紧力与上钢板振动加速度关系Fig.2 Relationship between vibration acceleration of the top plate and preload

1.3.2紧固件预紧力与松动寿命关系

图3为未喷丸及喷丸紧固件预紧力耐久极限测定曲线.由图3可见,2.8、2.0 kN分别为未喷丸和喷丸紧固件松动(失效)与不松动(不失效)的分界处,即耐久极限值.预紧力耐久极限越小,表明紧固件抵抗松动的能力越强.根据图3的结果,选取2.0 kN作为较低水平的预紧力.由于喷丸紧固件在该预紧力水平存在3根松动试样,因此,只需再测定3根未喷丸紧固件的松动寿命,结果如图4所示.由图4可见,在相同预紧力下,喷丸紧固件松动寿命明显高于未喷丸紧固件.可见,进行微粒子喷丸处理后,提高了镀锌紧固件的抗松动能力.

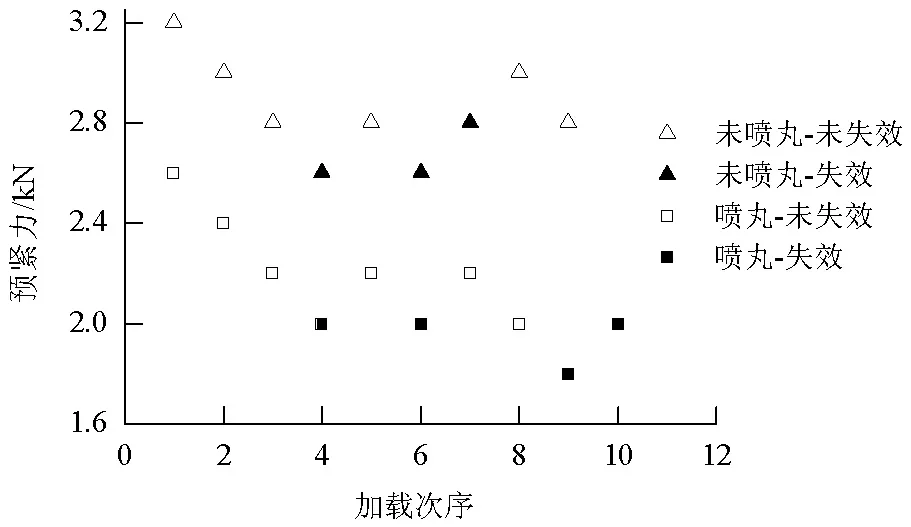
图3 未喷丸及喷丸紧固件预紧力耐久极限的测定Fig.3 Measurement of preload endurance limits of EZP and FPP-EZP

图4 预紧力2.0 kN时未喷丸及喷丸紧固件松动寿命Fig.4 Loosening life of EZP and FPP-EZP at the preload of 2.0 kN

1.3.3紧固件螺纹面形貌观察

使用扫描电镜分别观察图4中6根紧固件的螺纹面形貌.图5、6分别给出了两种紧固件各1根试样试验前、后螺纹面的观察结果.对比观察发现,虽然未喷丸紧固件的振动周次均比喷丸紧固件低,但未喷丸紧固件发生配合的两圈螺纹均产生明显磨损(试验用螺母只有两个整圈螺纹),其中,1#螺牙更靠近螺母支撑面,平均磨损深度为16.7 μm,2#螺牙平均磨损深度为6.5 μm,如图5(b)所示.放大观察发现未喷丸螺纹面出现明显的犁沟和较大的剥层,磨损程度严重,如图5(c)所示.喷丸螺纹面发生轻微磨损,磨损面较光滑,有较浅的犁沟存在,无剥层发生,如图6(b)、(c)所示.

上述试验结果表明,喷丸后紧固件抗松动能力的提高与螺纹面磨损程度的降低有关.

图5 未喷丸紧固件(2.0 kN，9.6×104次)试验前、后螺纹面形貌Fig.5 Surface morphology of thread for EZP before and after test (2.0 kN, 9.6×104 cycles)

图6 喷丸紧固件(2.0 kN，1.3×105次)试验前、后螺纹面形貌Fig.6 Surface morphology of thread for FPP-EZP before and after test (2.0 kN, 1.3×105 cycles)

2 数值计算

2.1 模型的建立

图7为螺纹紧固件连接结构变形及刚度模型.

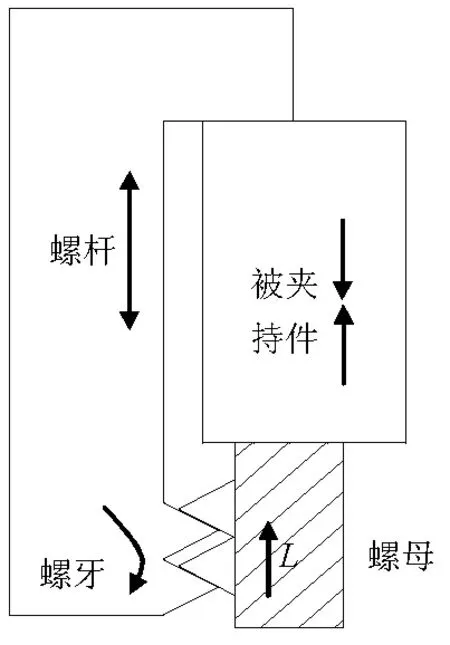
(a)

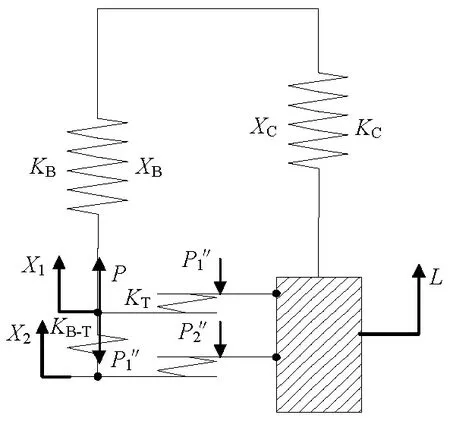
(b) 图7 螺纹紧固件连接结构变形及刚度模型Fig.7 Diagram of structure deformation and stiffness model of threaded fastener

如图7(a)所示，螺母在拧紧过程中会沿螺杆轴向产生位移L,使被夹持件压缩,螺杆拉伸,螺牙发生弯曲变形.由于螺母的高度明显小于该结构的其他部分,使得该部分刚度大,因此本研究认为螺母沿轴向为刚性的.

基于结构的变形,建立了图7(b)所示的紧固件刚度模型，图中：KB为螺杆光滑部分的刚度；KB-T为两螺牙间的刚度；KC为被夹持件的刚度；KT为螺牙弯曲变形刚度；X1、X2分别为螺杆1#、2#螺牙节点相对于螺母螺牙节点的位移；XB、XC分别为螺杆光滑部分和被夹持件的变形位移；节点及伸出的直线表示螺牙；结构的拉伸或压缩变形由图中的弹簧表示,变形认为是弹性的.

设紧固件拧紧后的预紧力为P,则螺杆光滑部分和被夹持件的受力可表示为

P=KBXB=KCXC.

(3)

(4)

螺杆螺牙节点产生的位移将由螺牙相同大小的弯曲变形进行匹配.螺牙由此产生弯曲变形力为

(5)

式中:hi为第i个螺牙螺纹面的磨损深度.

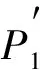
(6)

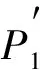
(7)

将式(3)～(5)代入式(6)、(7)，得

P=KCXC,

(8)

KCXC=KBXB,

(9)

KBXB=KB-T(X1-X2)+KT(X1-h1),

(10)

KB-T(X1-X2)=KT(X2-h2).

(11)

求解式(8)～(11)可得预紧力P施加后(此时hi=0),螺杆光滑部分、被夹持件以及两螺牙的初始变形位移X0B、X0C、X0i.根据螺栓连接结构的变形关系,拧紧螺母产生的轴向位移为

L=X0B+X0C+X01+X02.

(12)

当螺纹面开始产生磨损后,使得螺纹副间产生间隙,改变结构各部分的变形位移.但由于该仿真只计算由于磨损造成的预紧力的损伤量,认为最初沿轴向的位移不发生变化.因此,磨损深度与变形位移间满足变形协调关系，

L=XB+XC+X1+X2+h1+h2.

(13)

本文在紧固件刚度模型中引入Archad磨损模型[5-6],计算螺纹面磨损深度的变化.假设1#与2#螺牙滑移距离之比为2,接触应力均匀分布,则磨损深度随滑移距离Si的变化为

(14)

式中：At为螺纹面接触面积；κ为材料的磨损系数.

对式(14)求解,可得磨损深度随滑移距离的变化,方程的初始条件为Si=0,hi=0.将计算得到的磨损深度hi代入式(10)、(11),联立式(9)～(13),迭代求解,即可得到螺纹面磨损深度及预紧力随滑移距离的变化.

2.2 计算结果

参照前述试验条件,P=2.0 kN.根据M5螺栓结构的尺寸,At=10.56×10-6m2.各部分的轴向刚度可通过K=EA/l(E为材料弹性模量,A为横截面积,l为轴向长度)近似计算.KB取螺杆光滑部分长度,KB-T取螺距,KC取被夹持件长度.通过计算得到KB、KB-T、KC分别为 2.9×108、5.1×109、3.2×108N/m.螺牙弯曲变形刚度可根据悬臂梁的扰度公式近似推得KT=3EIZ/c3(IZ为螺牙截面矩,以螺牙3/4高度对应的螺牙截面进行求取；c为螺牙高度).通过计算得到KT=0.19×108N/m.螺纹紧固件材质为20#钢,通过模拟试验测试得到该材质的试样在滑动摩擦工况条件下磨损系数为7.5×10-14m2/N,下述计算取该值.

图8为计算得到的螺纹面磨损深度随滑移距离的变化曲线.由图8可见,螺纹面磨损深度逐渐增加,滑移初期增加速度较快,随后增加速度逐渐降低.1#螺牙磨损的深度更大,磨损的速度更快.试验中1#螺牙的磨损深度为16.7 μm,该深度在图8中对应的滑移距离为3.675 m,如A点所示.而此时2#螺牙对应的磨损深度为5.44 μm,如B点所示.计算得到结果略小于1.3.3节中的观察测量结果(平均深度6.5 μm).

图8 螺纹面磨损深度随滑移距离的变化曲线Fig.8 Relationship between thread wear depth and sliding distance

由于两螺牙磨损深度的变化趋势相似,现取1#螺牙的磨损深度作为横坐标,绘制图9所示的紧固件预紧力随螺纹面磨损深度的变化曲线.可见,螺纹面的磨损造成了紧固件预紧力的下降:当磨损深度小于20 μm时,紧固件预紧力基本呈线性降低;大于20 μm时,随着磨损深度的增加,预紧力降低速度逐渐加快.试验中,将预紧力为2.0 kN的三根未喷丸紧固件重新拧紧至初始标记的紧固位置,并将拧紧力矩值代入式(1),得到了试验中螺纹面发生磨损后紧固件的残余预紧力,并标在图中.可见,相同磨损深度下,试验测得的预紧力均大于仿真计算结果.由于试验中产生磨损并不是均匀分布在整个螺纹面上,这使得螺纹副间因磨损减少的配合距离小于图5中测得的磨损深度,测得结果偏大.图8、9的结果显示,试验与仿真计算的偏差较小,验证了该数值仿真计算方法的可行性.

通过仿真计算得到了螺纹面磨损深度与预紧力间的关系，进一步证实了螺纹面的磨损会造成预紧力的损失,且如果磨损持续发生,预紧力存在大幅快速下降的可能.因此,在考虑通过微粒子喷丸表面处理抑制该紧固件的松动时,表面硬化层的厚度需要大于20 μm.

综合微粒子喷丸未处理及处理的镀锌紧固件振动试验结果以及数值仿真计算结果,可知,横向振动条件下,螺纹面的相对滑移造成螺纹面的磨损,而磨损造成紧固件配合程度的降低,引起紧固件预紧力的减小,从而降低紧固件抵抗松动的能力.

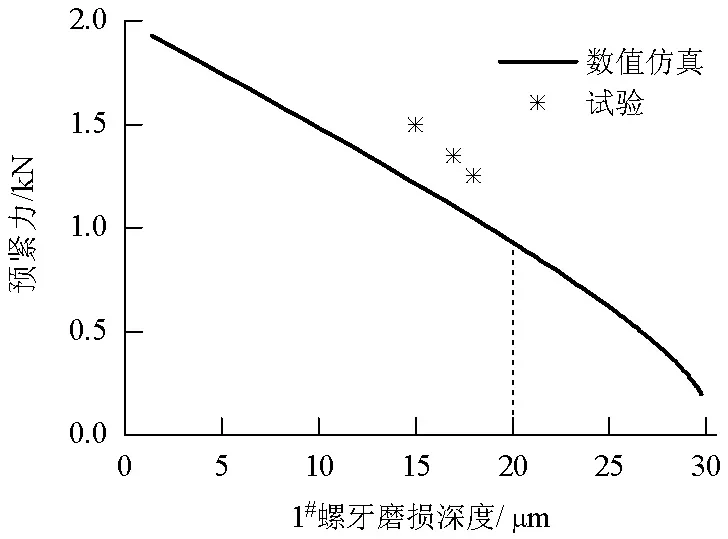
图9 预紧力随螺纹面磨损深度的变化Fig.9 The relationship between preload and wear depth

3 结 论

本文使用未喷丸及喷丸镀锌紧固件进行了紧固件横向振动试验,比较了两种紧固件抗松能力及试验后螺纹面形貌差异,基于数值计算,分析了螺纹面磨损深度改变对预紧力的影响,结论如下:

(1) 未喷丸紧固件的抗松动能力低于喷丸紧固件,未喷丸紧固件螺纹面发生严重磨损,而喷丸紧固件螺纹面磨损轻微.

(2) 螺纹面磨损深度随着滑移距离的增大而增加,紧固件预紧力随着螺纹面磨损深度的增加先呈线性降低,随后降低速度逐渐加快.

(3) 螺纹面的磨损引起预紧力下降,降低紧固件抵抗松动的能力.

致谢：国家重点实验室自主研究课题(2015TPL_T16).

[1] JUNKER G H. Criteria for self loosening of fasteners under vibration[J]. Aircraft Engineering and Aerospace Technology, 1972, 44(10): 14-16.

[2] PAI N G, HESS D P. Experimental study of loosening of threaded fasteners due to dynamic shear loads[J]. Journal of Sound & Vibration, 2002, 253: 585-602.

[3] YAMAMOTO A, KASEI S, KUBO T. Investigations on the self-loosening of threaded fasteners under transverse vibration[J]. Journal of the Japan Society of Precision Engineering, 1977, 43: 1069-1074.

[4] JIANG Y, ZHANG M, PARK T W, et al. An experimental investigation on self-loosening of bolted joints[J] Journal of Mechanical Design, 2004, 126(5): 925-931.

[5] ARCHARD J F. Contact and rubbing of flat surfaces[J]. Journal of Applied Physics, 1953, 24: 981-988.

[6] ARCHARD J F. Single contacts and multiple encounters[J]. Journal of Applied Physics, 1961, 32: 1420-1425.

[7] Sakai. Investigations of bolt loosening mechanisms[J]. Bulletin of the JSME 21,1978(159): 1391-1394.

[8] 侯世远,廖日东. 螺纹连接松动过程的研究现状与发展趋势[J]. 强度与环境,2014,41(2): 39-52.

HOU Shiyuan, LIAO Ridong. Research progress on self-loosening of threaded fasteners[J]. Structure & Environment Engineering, 2014, 41(2): 39-52.

[9] 于泽通,刘建华,张朝前,等. 轴向交变载荷作用下螺栓联接结构的松动试验研究[J]. 摩擦学学报,2015,35(6): 732-736.

YU Zetong, LIU Jianhua, ZHANG Chaoqian, et al. An experimental study on self-loosening of bolted joints under axial vibration[J]. Tribology, 2015, 35(6): 732-736.

[10] KIKUCHI S, SASAGO A, KOMOTORI J. Effect of simultaneous surface modification process on wear resistance of martensitic stainless steel[J]. Journal of Materials Processing Technology, 2009, 209(20): 6156-6160.

[11] BLANCHET T A. Coupled evolution of load distribution and wear on grease-lubricated lead screw threads[J]. Tribology Transactions, 2006, 49(4): 502-512.

[12] CROCCOLO D, AGOSTINIS M D, VINCENZI N. Failure analysis of bolted joints: Effect of friction coefficients in torque-preloading relationship[J]. Engineering Failure Analysis, 2011, 18(1): 364-373.

[13] 陈维金. 德国与我国机车车辆用螺栓技术的对比分析[J]. 铁道技术监督,2011,39(4): 2-7.

CHEN Weijin. Comparative analysis of the bolt technology using locomotive of China and Germany[J]. Railway Quality Control， 2011, 39(4): 2-7.

[14] CHEN J J, SHIH Y S. A study of the helical effect on the thread connection by three dimensional finite element analysis[J]. Nuclear Engineering & Design, 1999, 191(2): 109-116.