开裂钢筋混凝土梁正常服役有效惯性矩随机分析
2018-06-01陈文龙赵人达徐腾飞
杨 成, 陈文龙, 赵人达, 徐腾飞
(1. 西南交通大学陆地交通地质灾害防治技术国家工程实验室, 四川 成都 610031; 2. 重庆大学山地城镇建设与新技术教育部重点实验室, 重庆 400045)
在结构设计中,相比普通强度钢筋混凝土,高强度钢筋与高强度混凝土的使用,在保证相同承载能力的前提下,将有效降低构件的截面尺寸与配筋率[1],从而导致较大的变形与裂缝宽度.此时,能否满足正常使用极限状态的性能要求,可能成为结构设计的控制性因素[2-3].
混凝土梁开裂后的裂缝宽度、刚度计算是混凝土结构正常使用状态设计的重要内容[4].当计算钢筋混凝土梁的抗弯承载力时,混凝土抗拉强度通常可以忽略.但事实上,在正常使用极限状态范围内,受拉区裂缝之间的混凝土仍然承担部分拉力,为构件正截面抗弯提供刚度,被称为拉伸刚化效应[5-6],将影响钢筋混凝土构件的开裂后刚度、变形和裂缝宽度[7].对于配筋率较低的混凝土板而言,拉伸刚化效应可能会贡献50%以上的开裂后刚度[8].
正常使用极限范围下钢筋凝土结构变形的计算都需考虑混凝土的开裂非线性与拉伸刚化效应,非线性有限元法是其中一种重要的分析方法.可通过修改钢筋或混凝土材料的应力-应变关系来考虑拉伸刚化效应[9-11],也可基于粘结滑移理论及局部特性提出的有限元模型[12-13]来解决.虽然非线性有限元法能够比较准确地预测构件挠度,但其巨大的计算量与复杂性使得大部分工程师更愿意采用规范建议的简化公式.因此,1965年Branson提出了开裂混凝土有效惯性矩公式[14],并被ACI318-05[15]采用,但Bischoff认为,当配筋率较低时,Branson公式将会高估截面的有效刚度,并提出了与欧洲规范形式一致的有效惯性矩预测公式[1,16].我国《混凝土结构设计规范》采用刚度解析法并结合钢筋应力不均匀系数试验推导了混凝土截面的有效刚度[4,17],并开展相关试验研究,实测了拉伸刚化效应引起的钢筋应力变化[18].
但上述工作仍然存在问题,由于混凝土力学特性存在固有的随机性质,导致钢筋混凝土梁的拉伸刚化效应与有效刚度随之具有随机性,进而使钢筋混凝土梁的变形也不可避免地具有随机特性[19-20],客观上增加了对钢筋混凝土梁变形预测的难度,而这对当前大量使用的“桥建合一”铁路站房建筑设计将产生显著影响[21].由于站台楼面的轨道梁受建筑结构和高速铁路桥涵规范双重控制,梁体平顺性要求较普通建筑结构高.如果对钢筋混凝土结构拉伸刚化效应的随机性和混凝土开裂随机性的考虑缺失,过高或过低的轨道梁变形预测结果都将导致预拱度设置不合理,从而影响线路平顺与列车高速过站行车的安全性.这与普通建筑结构在重力荷载作用下只考虑单向变形可靠度有显著区别.文献[22]建立了混凝土结构的长期变形随机分析模型,利用该模型分析钢筋混凝土偏心受压柱长期变形的随机性.文献[23]提出开裂的随机性在混凝土结构随机分析的重要性,并提出分片响应面方法解决开裂非线性的钢筋混凝土梁变形随机问题.
本文采用刚度解析法[5]推导并化简了正常服役下钢筋混凝土梁有效惯性矩的无量纲形式.采用蒙特卡洛法对其进行随机分析,并用偏相关系数表示参数的敏感性,完成了敏感性分析,提出了钢筋混凝土梁有效惯性矩的预测均值模型与95%概率区间模型,对于随机分析背景下预测钢筋混凝土结构变形有一定意义.
1 有效惯性矩模型
根据我国GB 50010—2010《混凝土结构设计规范》,在裂缝稳定阶段,可以采用刚度解析法推导钢筋混凝土梁截面的平均刚度B(割线值).[5]
(1a)
(1b)
式中:
Es为钢筋的弹性模量;
As为受拉钢筋的面积;
h0为截面有效高度;
ψ为裂缝间受拉钢筋不均匀系数,通过试验得到[4];
η为开裂截面的钢筋内力臂系数;
αE为钢筋弹性模量与混凝土弹性模量的比值;
μ为受拉钢筋配筋率;
λ为受压变形塑形系数;
ω为混凝土受压区合力换算系数;
xcr为开裂截面的受压区高度;
Mcr为钢筋混凝土受弯构件截面开裂弯矩;
Ma为正常使用荷载作用下的弯矩.
在正常服役的荷载作用下,可以假定混凝土受压区混凝土处于线弹性阶段[3,24-25],此时式(1a)中的参数可简化为
(2)
将式(2)代入式(1a)有
(3)
对于矩形截面梁,式(3)两边同时除以EcIg,截面有效惯性矩为
(4)
式中:
Ig为未开裂截面惯性矩;
Ie为开裂钢筋混凝土梁的有效惯性矩;
h为矩形截面梁的横截面高度.其中梁和板的h0/h取值范围为0.8~0.9[1],本文以0.8为例进行分析.
2 随机参数和分析方法
钢筋混凝土构件挠度的不确定性主要由材料属性、制造误差、荷载及构件尺寸产生.由于式(4)为无量纲方程,所以忽略尺寸因素的影响.而随机分析是在加载过程中进行的,所以荷载的不确定性同样被忽略.
所涉及的随机变量见表1[26],其中:
βfc为混凝土材料抗压强度随机变量;
βEc为混凝土弹性模量随机变量;
βft为混凝土抗拉强度随机变量;
βEs为钢筋弹性模量随机变量;
Esm为钢筋弹性模量均值,取200 GPa;
fcm为混凝土抗压强度平均值;
ft为混凝土抗拉强度;
fc为混凝土抗压强度.
由于随机分析对象为显式函数,可采用蒙特卡洛方法直接模拟,抽样次数为10 000次.
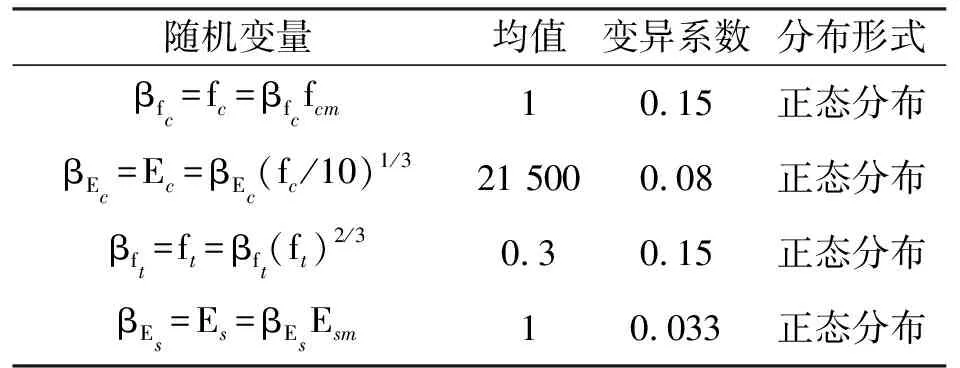
表1 随机变量的随机特性Tab.1 Statistical properties of random variables
3 均值和置信区间模型
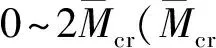
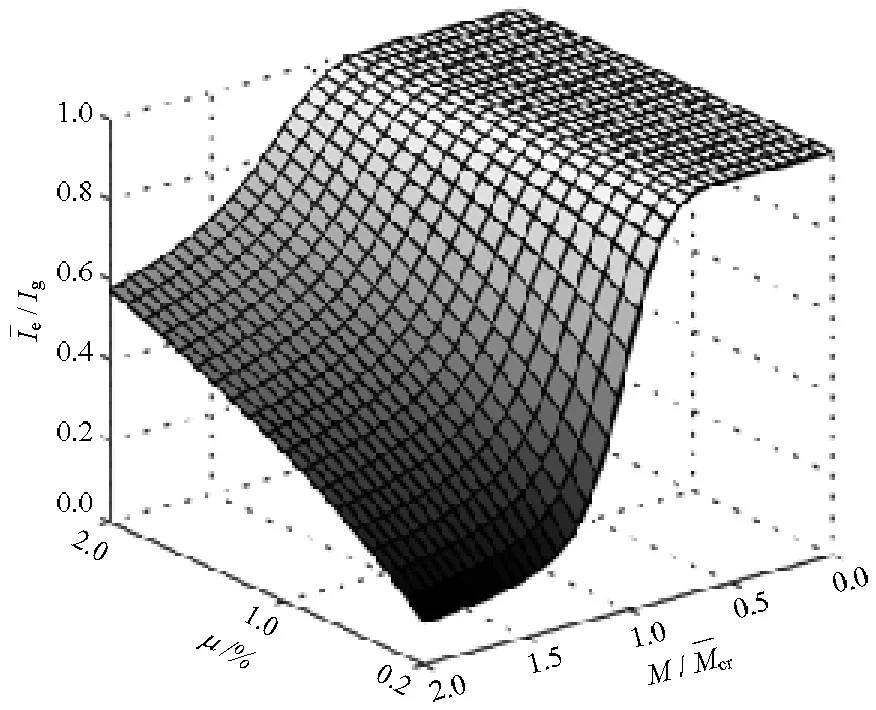
图1 无量纲截面惯性矩均值面Fig.1 Surface of the mean values of dimensionless moment of inertia
选择配筋率为0.3%与1.5%的情况,图2给出了混凝土抗压强度均值取30 MPa时随机分析均值与确定分析结果的对比.
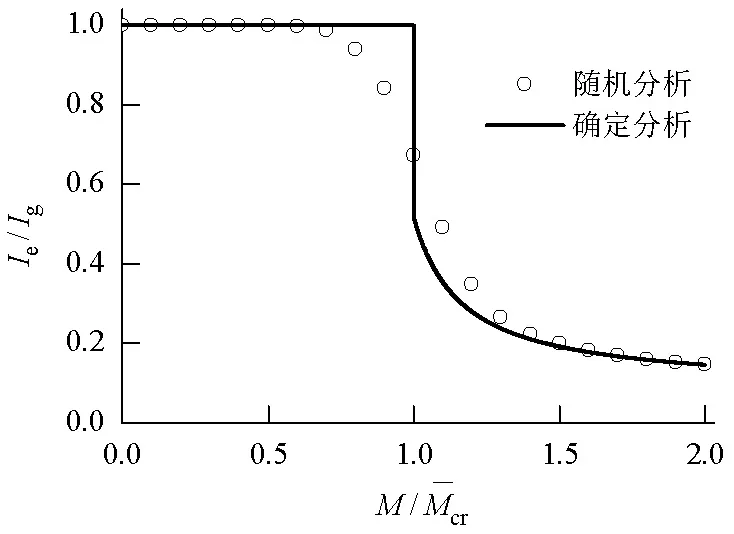
(a) μ=0.3%

(b) μ=1.5%图2 不同配筋率的无量纲截面惯性矩均值曲线对比Fig.2 Comparison of mean values of the dimensionless moment of inertia at varying reinforcement ratios
上述分析反映了截面开裂前,有效惯性矩为定值,即等于截面的惯性矩;而截面开裂后,采用式(4)给出的表达式计算.当外荷载接近开裂荷载时(左逼近开裂荷载),截面不会开裂,截面惯性矩为定值.但是对于随机分析而言,截面开裂是有一定几率的随机现象,当截面不开裂时,截面惯性矩等于确定分析结果;当截面开裂时,截面惯性矩小于确定分析结果,此时随机分析的均值亦小于确定分析结果.以此类推,可以得到当外荷载接近开裂荷载时(右逼近开裂荷载)的情况.因此从根本上说,确定性分析与随机分析结果的差异是由钢筋混凝土截面开裂发生的随机性与开裂前后刚度的差异共同引起的.对于不同配筋率的情况,高配筋率混凝土的裂缝深度浅,裂后刚度较大,与低配筋率混凝土相比,开裂前后的刚度差异较小,因此图2(b)中确定性分析结果与随机分析结果的差异较图2(a)小.
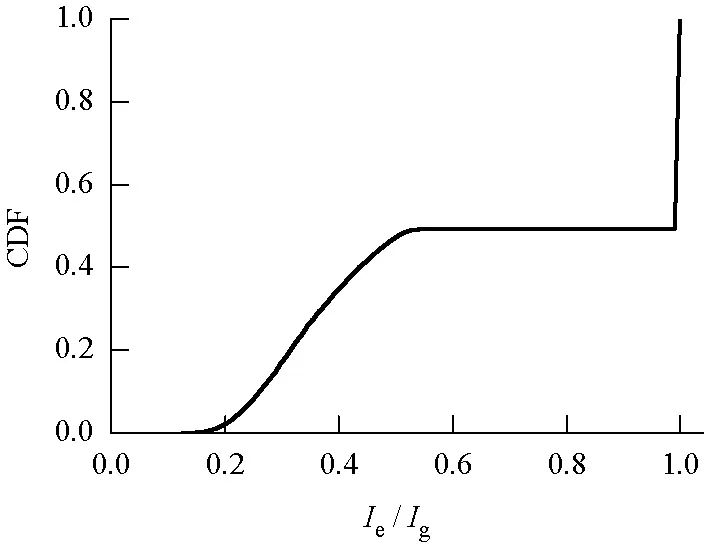

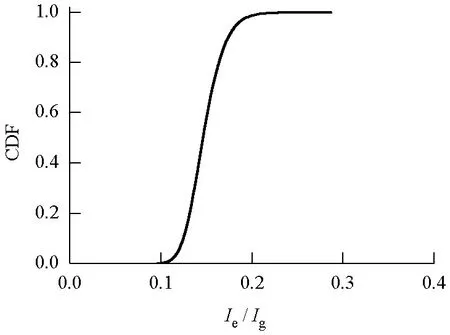
图3 无量纲截面惯性矩的累积函数分布Fig.3 Cumulative distribution function of the dimensionless moment of inertia
基于以上认识,Ie/Ig的均值可以写成
(5)
式中:
P(M≥Mcr)为截面开裂的概率;
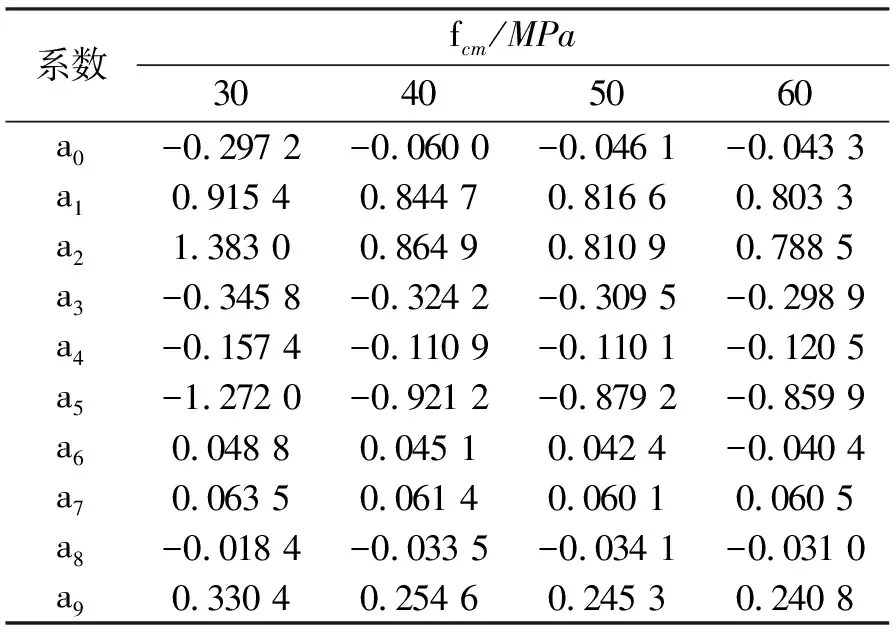
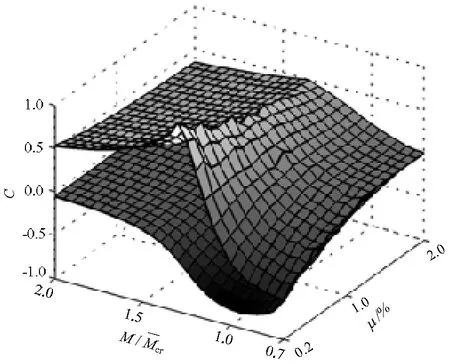
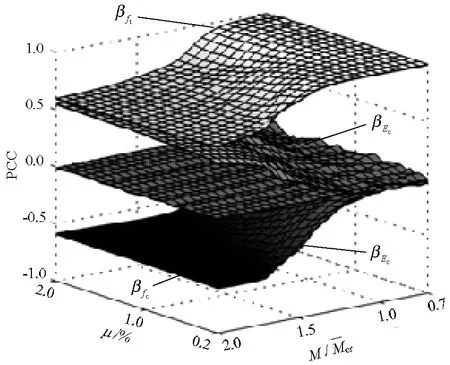
P(M E(Ie/Ig|M≥Mcr)为截面开裂条件下Ie/Ig的期望; E(Ie/Ig|M 显然, E(Ie/Ig|M (6) P(M≥Mcr)+P(M (7) 对于纯弯曲构件 (8) 式中: σ为截面端部拉应力; 由此,将式(5)~(8)联立,并结合图1中已求出的数据,E(Ie/Ig|M≥Mcr)可以用三次多项式拟合. (9) 式中,μ′=100μ. 表2给出了抗压强度均值分别取30、40、50 MPa与60 MPa时,式(9)的拟合系数. 表2 公式(9)的拟合系数Tab.2 Fitting coefficients for Eq. (9) 根据随机性累积分布分析,得到其非正态分布的置信区间为 (10) 式中,C为偏移系数. 图4 置信区间偏移系数Fig.4 Offset coefficient of the confidence interval 利用式(11)对曲面进行分段拟合,表3~6给出了不同外加弯矩的情况下,混凝土抗压强度均值分别取30、40、50 MPa与60 MPa时的拟合系数. (11) 表3 Csup的拟合系数Tab.3 Fitting coefficients for 敏感性分析是研究随机变量对结构响应贡献程度的有效方法.而对于具有大量统计样本的直接蒙特卡洛法而言,可采用多元回归分析中的偏相关系数(partial correlation coefficient, PCC)来代表变量的敏感性[27-29]. 表4 Csup的拟合系数Tab.4 Fittingcoefficients for 表5 Cinf的拟合系数Tab.5 Fittingcoefficients for 表6 Cinf的拟合系数Tab.6 Fittingcoefficients for 以混凝土抗压强度均值为30 MPa为例,图5给出了随机变量的敏感性曲面. 由图5中可以看出,混凝土抗压强度PCC值不会随着配筋率或外加弯矩的改变而有较大变化,其值为接近0的水平面,因此混凝土抗压强度对有效惯性矩不敏感.而对有效惯性矩较敏感的因素有混凝土抗拉强度、混凝土弹性模量与钢筋弹性模量.在加载早期,混凝土抗拉强度的敏感性接近1,随着荷载的增大,敏感性逐渐降低;同时,混凝土弹性模量和钢筋弹性模量对有效惯性矩的影响由0开始逐渐增加. 图5 随机变量的敏感性系数(PCC)Fig.5 Sensitivity coefficient of random variables (PCC) 刚度解析法为当前我国《混凝土结构设计规范》预测钢筋混凝土梁有效刚度的推荐方法,但由于混凝土自身的随机特性,导致钢筋混凝土梁有效刚度具有随机性,因此很难准确预测钢筋混凝土梁的变形,这对一些具有特殊使用功能的建筑结构有不利影响.旨在研究采用我国规范进行钢筋混凝土梁有效刚度预测时,预测结果的随机性. 当混凝土配筋率较低时,无量纲有效惯性矩随机分析的均值结果与确定分析的结果不一致; 给出了常用混凝土强度等级对应的量纲有效惯性矩的均值与置信区间(2.28%~97.72%)的数学模型; 混凝土抗拉强度对截面有效惯性矩较敏感,其敏感性随着荷载增大而降低;混凝土弹性模量与钢筋弹性模量的敏感性随着荷载的增大而增大;混凝土抗压强度对有效惯性矩不敏感. [1] BISCHOFF P H. Reevaluation of deflection prediction for concrete beams reinforced with steel and fiber-reinforced polymer bars[J]. Journal of Structural Engineering, 2005, 114(7): 1499-66. [2] 徐腾飞,白雪濛,赵人达. 加载过程中钢筋混凝土梁弯曲型变的随机性分析[J]. 西南交通大学学报,2015,50(4): 630-634. XU Tengfei, BAI Xuemeng, ZHAO Renda. Stochastic analysis of bending deflection for reinforced concrete beam in loading process[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 630-634. [3] GILBERT R I. Tension stiffening in lightly reinforced concrete slabs[J]. Journal of the Structural Division ASCE, 2007, 133(6): 899-903. [4] 丁大钧. 钢筋混凝土构件抗裂度、裂缝和刚度[M]. 南京:南京工学院出版社,1986: 17-26. [5] 过镇海,时旭东.钢筋混凝土原理和分析[M]. 北京:清华大学出版社,2007: 257-267. [6] 李志华,苏小卒. 钢筋混凝土受弯构件挠度计算方法综述分析[J]. 四川建筑科学研究,2011,37(2): 30-34. LI Zhihua, SU Xiaozu. Review of study on the methods for computing deflections of reinforced concrete flexural members[J]. Sichuan Building Science, 2011, 37(2): 30-34. [7] XU Tengfei, XIANG Tianyu, ZHAO Renda, et al. Stochastic analysis on flexural behavior of reinforced concrete beams based on piecewise response surface scheme[J]. Engineering Failure Analysis, 2016, 59: 211-222. [8] GILBERT R I, WARNER R F. Tension stiffening in reinforced concrete slabs[J]. Journal of the Structural Division, 1978, 104(2): 1885-2900. [9] BALAKRISHAN S, MURRAY D W. Concrete constitutive model for NLFE analysis of structures[J]. Journal of Structural Engineering, 1988, 114(7): 1449-1466. [10] COLLINS M P, VECCHIO F J. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Journal, 1986, 83(2): 219-231. [11] PARKHYA G K., MORLEY C T. Tension stiffening and moment-curvature relation for reinforced concrete elements[J]. ACI Journal, 1990, 87(5): 597-605. [12] FLOEGL H, MANG H A. Tension stiffening concept based on bond slip[J]. Journal of the Structural Division ASCE, 1982, 108(12): 2681-2701. [13] CHOIL C K, CHEUNG S H. Tension stiffening model for planar reinforced concrete members[J]. Computers and Structures, 1996, 59(1): 179-190. [14] BRANSON D E. Instantaneous and time-dependent deflections of simple and continuous reinforced concrete beams[R]. Alabama: Alabama Highway Department, 1963. [15] ACI Committee 318. ACI 318-05 building code requirements for structural concrete[S]. Washington D. C.: American Concrete Institute, 2005. [16] BISCHOFF P H, ANDREW S. Effective moment of inertia for calculating defections of concrete moment containing steel reinforcement and fiber-Reinforced polymer reinforcement[J]. ACI Structural Journal, 2007, 104(1): 68-5. [17] 中华人民共和国住房与建设保障部. GB50010——2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010. [18] 姜磊,姚继涛,信任,等. 验研究钢筋混凝土薄板受拉刚化效应[J]. 混凝土,2011(1): 62-64. JIANG Lei, YAO Jitao, XIN Ren, et al. Tension stiffening in reinforced concrete slabs and test research[J]. Concrete, 2011(1): 62-64. [19] JUNG J K, MAHMOUD M R T, HYUK-CHUN N, et al. Reliability analysis to resolve difficulty in choosing from alternative deflection models of RC beams[J]. Mechanical Systems and Signal Processing, 2013, 37: 240-252. [20] 周婧,陈秦,王慧英. 钢筋混凝土框架结构竖向不规则参数的概率评估[J]. 建筑结构学报,2014,35(3): 39-45. ZHOU Jing, CHEN Qin, WANG Huiying. Probability evaluation of vertical regularity parameters for reinforced concrete frame structures[J]. Journal of Building Structures, 2014, 35(3): 39-45. [21] 褚松涛,曹少卫,高夕良. 成都东客站承轨层桥建合一结构设计施工综合技术[J]. 建筑施工,2010,32(6): 520-524. CHU Songtao, CAO Shaowei, GAO Xiliang. Comprehensive techonogy of structure design and construction for bridge and building combined rail bearing floor of cheng du east railway station[J]. Building Construction, 2010, 32(6): 520-524. [22] 徐腾飞,向天宇,赵人达. 偏心钢筋混凝土受压柱长期变形分析[J]. 西南交通大学学报,2014,49(4): 26-630. XU Tengfei, XIANG Tianyu, ZHAO Renda. Long-term random deflection of eccentrically load RC column[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 26-630. [23] 徐腾飞,向天宇,白雪濛,等. 基于分片响应面的钢筋混凝土梁变形随机模拟[J]. 工程力学,2014,31(11): 170-174. XU Tengfei, XIANG Tianyu, BAI Xuemeng, et al. Stochastic simulation of reinforced concrete beam with piecewise response surface[J]. Engineering Mechanics, 2014, 31(11): 170-174. [24] XU Tengfei, CASTEL A, GILBERT R I, et al. Modeling the tensile steel reinforcement strain in RC-beams subjected to cycles of loading and unloading[J]. Engineering Structures, 2016, 126: 92-105. [25] XU Tengfei, CASTEL A. Modeling the dynamic stiffness of cracked reinforced concrete beams under low-amplitude vibration loads[J]. Journal of Sound and Vibration, 2016, 368: 135-147. [26] VAL D V, STEWART M G, MELCHERS R E. Effect of reinforcement corrosion reliability of highway bridges[J]. Engineering Structure, 1998, 20(97): 1010-1019. [27] YANG I H. Prediction of time-dependent effects in concrete structures using early measurement data[J]. Engineering Structures, 2007, 29: 2701-2710. [28] YANG I H.. Uncertainty and sensitivity analysis of time-dependent effects in concrete structures[J]. Engineering Structures, 2007, 29: 1366-1374. [29] 徐腾飞,吴涤,汪军,等. 预应力混凝土简支足尺试验梁变形随机分析[J]. 中国公路学报,2015,28(9): 67-72. XU Tengfei, WU Di, WANG Jun, et al. Stochastic analysis of deflection of prestressed concrete simply supported full-scale test beam[J]. China Journal of Highway and Transport, 2015, 28(9): 67-72.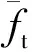
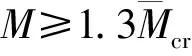
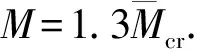
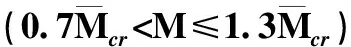
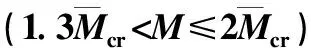
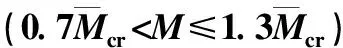
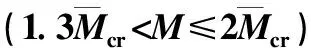
4 结 论
