任何密封受压时都应有0.5比的泊松变形能力——也作《徐氏流体密封与流动理论论文专集》的局部修正陈述

，

(保一集团有限公司， 浙江 温州 325105)

1 徐氏密封结构理念完整重述[1]

任何密封环都应能将其受到的加载压力有效瞬间正交转换为其密封应力，例如将杆的压紧密封环的活轴向紧固压力有效瞬间转换为环的活径向密封应力，将自紧面密封环柱面上的活流体压力如数瞬间转换为环端面上的活密封应力。能将压力有效瞬间正交转换的液体是因其软和体积不可压缩，软致其一受压便有变形流动力，体积不可压缩则致其一受压各向便有相同变形流动力。泊松比μ为0～0.5的普通物质既有固性行为又有液性行为，而且泊松比越趋近0.5的物质越具有充分液性行为和体积不可压缩性[2]，而越可有效瞬间完成这种转换。因此，密封环设计在于确保密封环时刻都有0.5比的泊松变形能力。然而，现有密封技术却不知密封对泊松变形的依赖性。

橡胶是非常软而泊松比值又非常趋近0.5的材料，因而可视为是一种稠得在大气温度、压力下还有固定形状的全液体。无芯橡胶O形环就可模拟为一环装满液体的无限薄壁金属管，用无限薄壁金属管代表液体的固定形状。首先由无芯橡胶O形环与其模拟金属环管应有相同的周向抗绷伸能力可知(式中的→指等式变换)：

2πruδkRmk=πru2Rmr→2πrukruRmk=
πru2Rmr→kRmk=0.5Rmr

(1)

然后由普通金属薄壁管能承受的极限压力pm=Rmδ/r可以知道，作为同一无芯橡胶O形环的模拟金属薄壁环管在容腔中能承受的极限压力pme不仅随最大挤出弧半径re而变，而且与re之积还为常数，即：

pmere≡Rmkδk=常数→pmere=
Rmkkru=0.5Rmrru

(2)

也就是说，安装入容腔的模拟金属环管能承受的极限压力为：

(3)

未安装入容腔的模拟金属环管能承受的极限压力为：

pmu=0.5Rmr

(4)

或者说，无芯橡胶O形环的受压应力或内部压力为：

px=0.5Rmrru/rx

(5)

式(1)～式(5)中，ru为全部外表面未受压时无芯橡胶O形环的横截面半径或自由挤出圆弧半径，re为无芯橡胶O形环穿过容腔最大闭合间隙的挤出圆弧半径(等于0.5倍容腔最大闭合间隙)，rx为部分外表面受压时无芯橡胶O形环未受压表面的挤出圆弧半径，r为普通金属薄壁管的横截面半径，δk为模拟金属环管壁厚，δ为普通金属薄壁管壁厚，mm；Rmk为模拟金属环管材料极限强度，Rmr为橡胶O形环材料极限强度，Rm为普通金属薄壁管材料极限强度，MPa。

由式(5)可以知道，①当安装致其挤出圆弧半径rx=0.5ru时，无芯O形环的内压力px0.5(安装应力Sa0.5)等于材料极限强度Rmr，或者说无芯O形环横截面直径压缩50%时的受压应力px正好等于密封环材料强度极限Rmr。②致无芯O形环密封面挤入泄漏微坑和微槽的密封微拉伸变形只能发生在其受压应力px等于材料强度极限Rmr而无拉伸抗力时，因为Rmr未变0而还有拉伸抗力的密封面发生致其rx≈0的密封微拉伸变形需要其受压应力px≈∞。

文献[3]认为，常温下的橡胶，就其分子链段运动来看是液体，就其整个分子链来看是固体。文献[4]认为，橡胶分子链受拉伸时趋于更整齐排列(似晶体化过程)而致橡胶更具固性行为，受压缩时趋于更卷曲(似去晶体化过程)而致橡胶更具液性行为。文献[5-6]认为，材料的泊松比，屈服前随拉伸载荷增加而降变至0，屈服后强化前又随载荷增加而升变至0.5。因此，可视未安装入容腔的橡胶O形环为横截面上有同心圆形弹性纤维线的液体环(图1b)；可视安装入正方形容腔的橡胶O形环为横截面上有同心正方形弹性纤维线的液体环(图1c)(ra为安装入容腔后的挤出圆弧半径)，但四角被绷伸致更强而能耐更高的压力；可视容腔中受足够压缩的橡胶O形环为只在内切圆外的挤出角内才有密集弧形弹性纤维线的液体环(图1d)，即其内切圆区被充分压缩至更具可如数各向相同传递压力的液性行为，其挤出角区被充分绷伸至更具能承受挤出压力的固性行为。

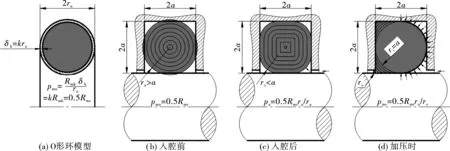
图1 无芯橡胶O形环在正方形容腔中的变形

因容腔中受流体挤压时的橡胶O形环被约束至无法发生任何泊松变形，故其约束模量M为：

M=[E(1-μ)]/[(1+μ)(1-2μ)]

(6)

当μ=0.5时M=∞，当μ=0时M=E。

由式(6)可知，被绷伸至泊松比逼近0[4-5]的挤出角内的环料因只有逼近弹性模量E的抗拉模量才有可能发生绷伸破损，被压缩至泊松比更逼近0.5的内切圆内环料有接近无穷大的抗压模量而完全不可能发生任何压缩破损，即被压缩至有充分液性行为而无拉伸抗力的环料可随其被解压缩或被再拉伸而逐渐恢复拉伸抗力。

Parker公司采用内径123.19 mm(4.850英寸)的丁基橡胶O形环作面密封(图2a)，在25 ℃和0.41 MPa下进行其横截面直径分别安装压缩15%、30%和50%时的泄漏测试，得到如图2b所示的O形环的安装压缩百分数(压缩百分数=[(ru-ra)/ru]×100%)与泄漏率关系曲线[7](图2b纵坐标单位中英寸线是指按英寸计量的密封线长。为尊重原文，更明确表达泄漏率意义，此处仍保留英寸线用法)。Parker公司的泄漏率曲线表明，橡胶O形环上涂脂可减少安装压缩量低于50%的O形环的泄漏，但却不能减少安装压缩量等于50%的O形环的泄漏[7]。

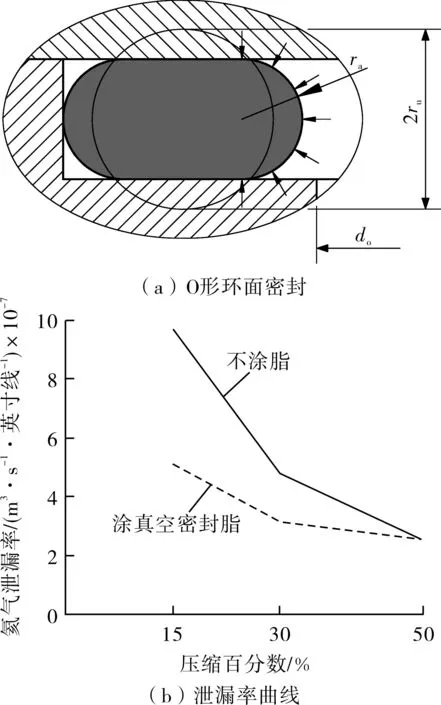
图2 Parker公司测试的O形环泄漏率与安装压缩百分数关系曲线

既然致无芯O形环横截面直径被压缩50%时的受压应力才致其密封面刚变至无拉伸抗力状态，那么压缩量低于50%而还有拉伸抗力的密封面就不可能直接被任何高的内压力挤入泄漏微坑和微槽而堵死泄漏通道，只能将无拉伸抗力的油脂部分挤入泄漏微坑和微槽而部分堵死泄漏通道， 因为压缩量越小和越大对应产生的越低和越高的内压力只能通过密封面对密封脂产生致泄漏对应部分减少越小和越大的挤压力。此外，压缩量等于50%而无拉伸抗力的密封面还需要一个不小于大气压力(0.1 MPa)的内部附加压力增量，才能以微拉伸变形方式将密封面挤入泄漏微坑和微槽而挤出其中的空气，而此时Parker公司的0.41 MPa测试压力远小于大小等于环材极限强度的内压力，根本不可能致其内压力增加而致其产生密封微拉伸变形。也就是说，Parker公司已无意提前证明式(5)是正确的。

由于充分无漏连接是加载密封接触层至其充分变形接触后再至其充分紧密接触的结果，即充分无漏连接需要先创造一个能充分填平密封接触面上凸凹不平的变形接触，后创造一个充分抗流体最强渗穿的紧密接触，而受约束压缩环的密封接触层或面的有效抗拉弹性模量Ec是密封变形和紧密接触的抗力指标，密封接触层或面的基体的有效抗拉弹性模量Es是至/持密封变形和紧密接触的动力指标，因此，密封环至/持密封的难度是由其接触层或面与其基体的材料的有效抗拉弹性模量之比m1(m1=Ec/Es)决定的，而且因Ec=Es而致m1max=1的橡胶O形环是最难至/持密封的[8]。

所以，理论和实验都证明，大气温度压力下密封要求的初始密封应力为Si=Rm+0.2 MPa。其中Rm等于密封面材料抗拉强度，并且是将初始密封面就位压缩成无拉伸抗力的半成品密封面所需的应力。0.2 MPa为大气温度压力下致半成品密封面达到和维持充分紧密接触所需的最大附加应力，并是密封的最小必须密封应力y的极大值，因为大气温度压力下弹性体(橡胶)和无拉伸抗力体的半成品密封面达到充分密封变形都需要0.1 MPa的附加应力，但是对于密封变形的维持，前者需要而后者不需要0.1 MPa的附加应力。对达到充分抗大气渗穿的紧密接触，两种合格密封面都需0.1 MPa的附加应力，即弹性体(橡胶)的最小必须密封应力y=0.2 MPa，无拉伸抗力体的最小必须密封应力y=0.1 MPa，或者说总体上密封的最小必须密封应力y≤0.2 MPa。

然而，ASME却一直将密封就位加工或安装至无可见泄漏时所需的应力(相当于前述的初始密封应力Si)误为密封所需的最小必须密封应力，因而将最难至/持密封的橡胶O形环密封误为最易至/持密封的[9]。

综上所述可知，密封设计在于确保受压密封元依赖泊松效应获得充分的变形，完全不同于旨在确保承载结构元的变形或应力不得超过材料的许可极限的普通机械设计。因此，一直远离泊松效应密封设计理念的现有密封技术，不可能为当今世界提供任何科学的密封结构。事实上，除此之外，现有技术还不知道漏阻(紧密度)物理量及任何有关它的计量、检测和控制手段[10-11]，现有密封技术标准是不科学的。

2 泊松变形能力补偿

2.1 材料泊松比及其变化

文献[12]指出，蠕动是固体在其同比温度大于0.5°时普遍发生的滞后应力的永久塑性应变(注：同比温度为与热力学温度不同计量单位的温度，同比温度0°为-273.16 ℃，同比温度1°为物质的熔点温度。文中保留原文献用法)，蠕动应变是由短时滞后的变形应变和长时滞后的黏流应变叠加构成的(图3)，蠕动应变随应力σ和温度T的增加而增加(图4～图5)，因此，可以说，材料的应变在其同比温度于0.5°时不仅会随温度和应力变化而且还是滞后于应力变化的。由于泊松比μ是物质的非加载方向与加载方向的应变比，因此，可以说，材料的泊松比值不仅随温度和加载压力大小而变，而且还是滞后加载压力变化的。

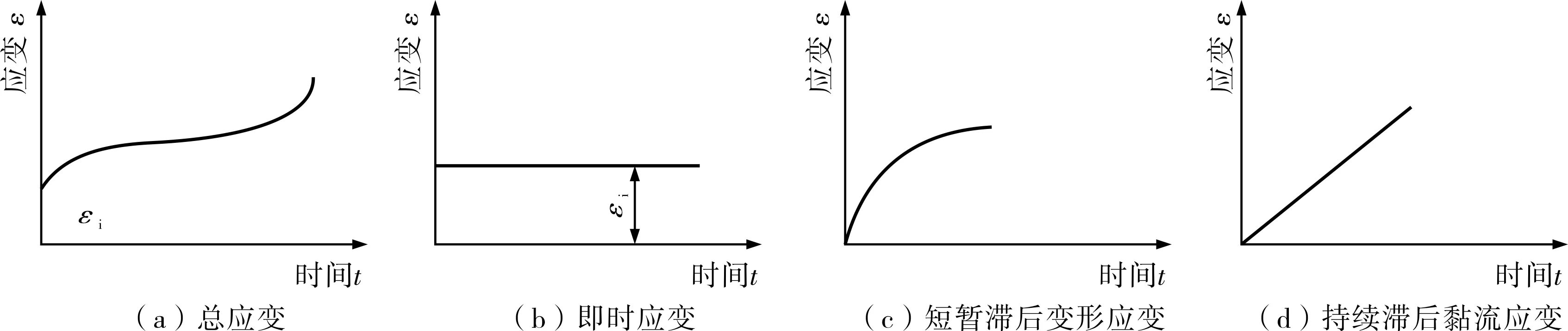
图3 蠕动应变构成与叠加

图4 恒温下蠕动应变量随应力增加而增大

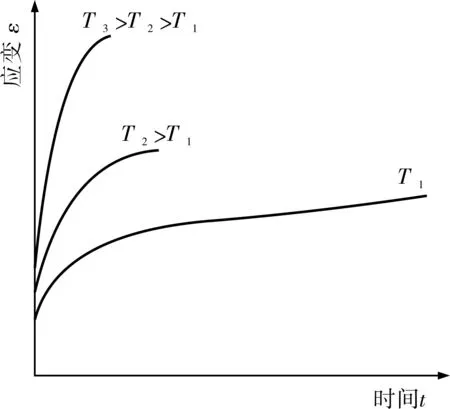
图5 恒应力下蠕动应变量随温度增加而增大

松弛和蠕动中材料泊松比值随松弛强度Δ的变化情况见图6[13]。由图6a～图6c可见，松弛和蠕动中材料的泊松比值几乎与松弛和蠕变一样，都是随松弛强度Δ递增而递增逼近0.5。由于松弛强度Δ=(E0-E∞)/E∞，为松弛终结后的弹性模量降低量与最终弹性模量之比[13]，而弹性模量E只有在材料屈服后才会随加载应力变化，因此，Δ越大代表载荷越大，进而可以说，密封材料屈服后的泊松比值是随加载压力递增而滞后加载压力递增逼近0.5的。

图6 松弛和蠕动中材料泊松比值随松弛强度Δ变化情况

泊松比μ的表达式为：

(7)

由式(7)可知，常温下物质的泊松比是其剪切模量G与体积模量K之比的函数(图7)[2]，并且当K/G逼近0时，μ逼近-1；当G/K逼近0时，μ逼近0.5。也就是说，越软而体积又越不可压缩的物质的泊松比越逼近液体的0.5比的泊松比，或者说，物质的泊松比是其液性行为指数，泊松比越逼近0.5的物质的液性行为和不可压缩性越强，乃至可视普通液体为泊松比μ=0.5的物质，可视普通固体为0<μ<0.5的物质。

图7 物质泊松比与K/G关系

由于同比温度为1°和0°的物质分别是其最柔软的液态和最坚硬的固态，因此，同比温度越大于和越小于0.5°的物质分别有越多的液性和固性行为。由于常温下不同物质的同比温度是不同的，因此，常温下的不同物质有不同的泊松比，因而有不同的液性行为(图7)。由于物质的温度越高越逼近变成其最柔软的液态，因此，恒定应力下温度T越高的物质其应变越大(图5)。

日本的一项测试证明，对等规聚丙烯，在其屈服前，泊松比随着拉伸降变至0(Ⅰ-Ⅱ)；在其屈服后强化前，泊松比随着进一步拉伸又升变至0.5(Ⅲ)；在强化后断裂前，泊松比随着更进一步拉伸又再降变至0(Ⅳ)，见图8[5]。

中国的一项测试证明，Q235钢经不高于400 ℃退火处理后屈服强度ReH几乎无变化，经1 000 ℃退火处理之后ReH大约下降60%。分别经1 000 ℃和200 ℃退火处理过的Q235钢，屈服后其泊松比都逼近0.5(图9)[6]。

图9 Q235钢屈服前后泊松比变化

综上所述，任何金属和非金属材料在屈服前和屈服后的泊松比值，不仅都随温度、载荷和载荷作用时间而变，而且还均随其温度逼近熔点和载荷逼近抗拉极限而逼近0.5。因此，密封设计者都应当知道材料的泊松比值变化对密封的泄漏是否产生影响，如果有影响又如何解决。

2.2 泊松变形能力补偿角

自紧密封的实质是使密封环如数正交传递流体压力，例如，是使图10所示的自紧密环将其内柱面上的流体压力p如数转换为其端面上的密封应力S，因此，任何自紧密环都应拥有充分的液性行为。图10中k为环高h与环壁厚b之比，Ød2为环外径，Ød1r为环内径。

图10 自紧密封实质

由于泊松比越逼近0.5的物质越具有充分液性行为和不可压缩性而越可有效瞬间正交传递压力，因此，一切柔韧固体材料，无论其泊松比值比0.5小多少，都可通过一个液性补偿角θl将其正交应变比补偿到0.5而用于制作自紧密环。材料的泊松变形补偿情况见图11。

图11 材料的泊松变形补偿

材料的泊松变形抵消情况见图12。图中Ød2′为环腔壁直径。任何与其缚腔有径向间隙C的自紧密环，在流体压力到来时，都将因压力下径向间隙所致的环周增加所伴随的环高泊松变形减少而脱离紧密接触。由于构件制造误差和材料热胀冷缩系数差都会致环径向接触有间隙，因此，即使对泊松比为0.5的自紧密环，也还需要一个径向接触补偿角θc，才能及时抵消径向间隙所致的与泊松比值成正比的受压正交变形。

图12 材料的泊松变形抵消

由于泊松比为0～0.5的自紧密环的液性补偿(图11)和接触补偿(图12)都是必须的，而且都是补偿流体压力下的环高的减少，因此，如果其液性补偿统一按0补偿到0.5，其接触补偿统一按0.5补偿到0，则任何自紧密环都有因泊松比值变化极限值(0.5)相同决定的充分液性补偿角θl和充分接触补偿角θc，并可统称为基本泊松变形补偿角θe=arctan(μh)/r=arctan(h/d)[8]。其中h为密封环高，d为密封环内径，μ取泊松比极限值0.5。

如果自紧密环的基本泊松变形补偿角θe有楔功能，则也是致环更多获得有用的密封变形。因此，无论θe再大，所改变的仅是环材达到正交变形比值极限的时间而不是极限值，或至多是将环材的正交变形比μ尽早由0补偿到0.5或由0.5抵消到0，或至多是消除环材的正交变形比μ的滞后性。所以，一切材料的自紧密环，无论其材质实际泊松比值多大，都可以用一个比基本泊松变形补偿角θe更大的角度θx，同时用作其泊松变形补偿角θl和抵消角θc。

由于基本泊松变形补偿角θe能将泊松比由0补偿到0.5，因此，无论泊松比怎样随材质及其温度和压力变化，一个大于基本泊松变形补偿角θe的实际泊松变形补偿角θx，都能确保密封环一受压移动便有0.5比的泊松变形能力。也就是说，设计密封环时只须考虑环是否拥有足够大的泊松变形补偿角，无需追究泊松比值是如何具体随材质及其温度和压力变化的。

密封环的泊松变形补偿角的实质是确保环容腔能致环一受压便能产生由大空间至小空间的移动，使在大空间具备与不具备0.5比泊松变形能力的各环层，在压入小空间瞬间都有0.5比的泊松变形能力，等同致密封环时刻都有0.5比的泊松变形能力。其实，在那种容腔中受加载压缩的密封环，因受被密封面充分约束而不可能产生任何泊松变形，必定为那种有能力发生而又不会发生泊松变形的环。如果将环的这种泊松变形视为密封环被被密封面由小空间回压入大空间的变形，则密封环在大空间也是不可压缩的，从而致密封面在大小空间时都能产生等于加载压力的密封应力。所以，密封设计合格性的首要判据是看密封环是否一受压便有角度不小于θe=arctan(h/d)的由大至小的移动空间。

3 密封脂或剂的应用场合

如图13所示，受到2个刚性表面压缩的厚物体，有2个受到有充分约束压缩而不能产生任何泊松变形的薄接触层，和1个未受到充分约束压缩而可发生一些泊松鼓出变形的厚腰。因此，被2个刚性被密封表面压缩成再无料可挤出的密封脂或剂薄膜便是一个无任何鼓出腰的完全受到充分约束压缩的物体[14]。

图13 约束与非约束压缩

由于被约束压缩至无任何抗拉能力又无任何宏观应变的材料既无压缩破损又逼近0.5的泊松比[5-6]，因此，根据式(6)可知，被2个刚性被密封表面压缩至无料可挤出的密封脂或剂薄膜有逼近无穷大的弹性模量，使其最大许可压力只受其压缩表面的强度限制。所以，密封脂或剂的密封性和许可工作压力完全取决于致其形成一个逼近无限强膜的充分周向均匀受压。确保螺栓连接端面达到充分周向均匀受压的手段是在连接的特设端面上增加一个齿顶与对接面齐平的边缘宏观锯齿环[15]，确保螺纹连接端面达到充分均匀受压的手段是确保端面与螺纹轴线垂直。确保这两种连接端面都达到充分强受压的手段是确保其连接都能通过4倍许可工作压力的破裂压力测试。

流体压力下啮合螺纹间的密封脂或剂也是受约束压缩的，根据式(5)，只要确保其无挤出间隙，也可确保其连接能承受逼近无穷大的流体压力。确保密封脂或剂无挤出间隙的手段是使用在最后啮合的螺纹中无任何不完整螺纹的柱/锥螺纹配合，以确保初始啮合螺纹为多圈无任何牙顶/牙底啮合的紧固螺纹，最后啮合螺纹为一圈有牙顶/牙底充分啮合的密封螺纹，分别用作实现和维持无密封脂或剂挤出间隙连接所需的动力条件和变形条件[15]。

由于确保密封脂或剂充分周向均匀受压的各种手段都是普通和廉价的，因此，脂或剂密封是最廉价、最简单和最可靠的密封，本应在各行业得到广泛的应用。

4 O形环密封的应用场合

矩形容腔中的橡胶O形环任何时候都只有一个固定不变的压力流体暴露表面积，无法以同一容腔既致环的流体密封作用力大于环的流体去密封作用力，又致环被安装至初始密封状态，即无法以同一容腔既致环在工作中的ra≥ 0.75ru(图14a)，又致环安装至ra≤0.5ru(图14b)[7]。图14中φd12为杆柱外径。

如果无芯橡胶O形环的容腔是一个以容腔多边形内切圆为基础的圆壁容腔(图15)，则O形环在容腔中只会有一个流体挤压角和一个自由挤出角，因此，微弱的流体压力便可致O形环在挤压角里无阻力地由小空间至大空间移动而致其顷刻脱离容腔圆壁，从而致其流体作用面积和密封作用力陡增而致其在自由挤出角里由大空间至小空间移动，同时达到充分变形接触和充分紧密接触。

现有密封技术一直未注意到有关无芯橡胶O形环密封的如下基本面：①橡胶材料摩擦因数巨大(有1～4)，橡胶O形环在标准化矩形容腔中有3～4倍流体暴露或流体操纵面积那样巨大的摩擦接触面积，需要很高的流体压力才能致橡胶O形环开始由大空间至小空间的密封变形移动。②薄壁管能承受的极限压力与管壁半径成反比，容腔中受压缩的橡胶O形环的内部和外部压力场不可能有任何跃变区域，因而任何腔中的O形环只能以壁相切的等圆弧面去适应其内外压力。③容腔中受约束压缩的橡胶O形环为一种可像液体一样沿腔流动而又有无限抗压能力和有限抗拉能力的物体，以至于其耐压极限是按式(5)由其在挤出角的拉伸变形决定的。因此，现有密封技术既不知道橡胶O形环在容腔中如何变形，如未意识到其流体暴露表面应为等径圆弧[16-18]，又不知道如何设计O形环密封，如不知道如何计算其耐压。

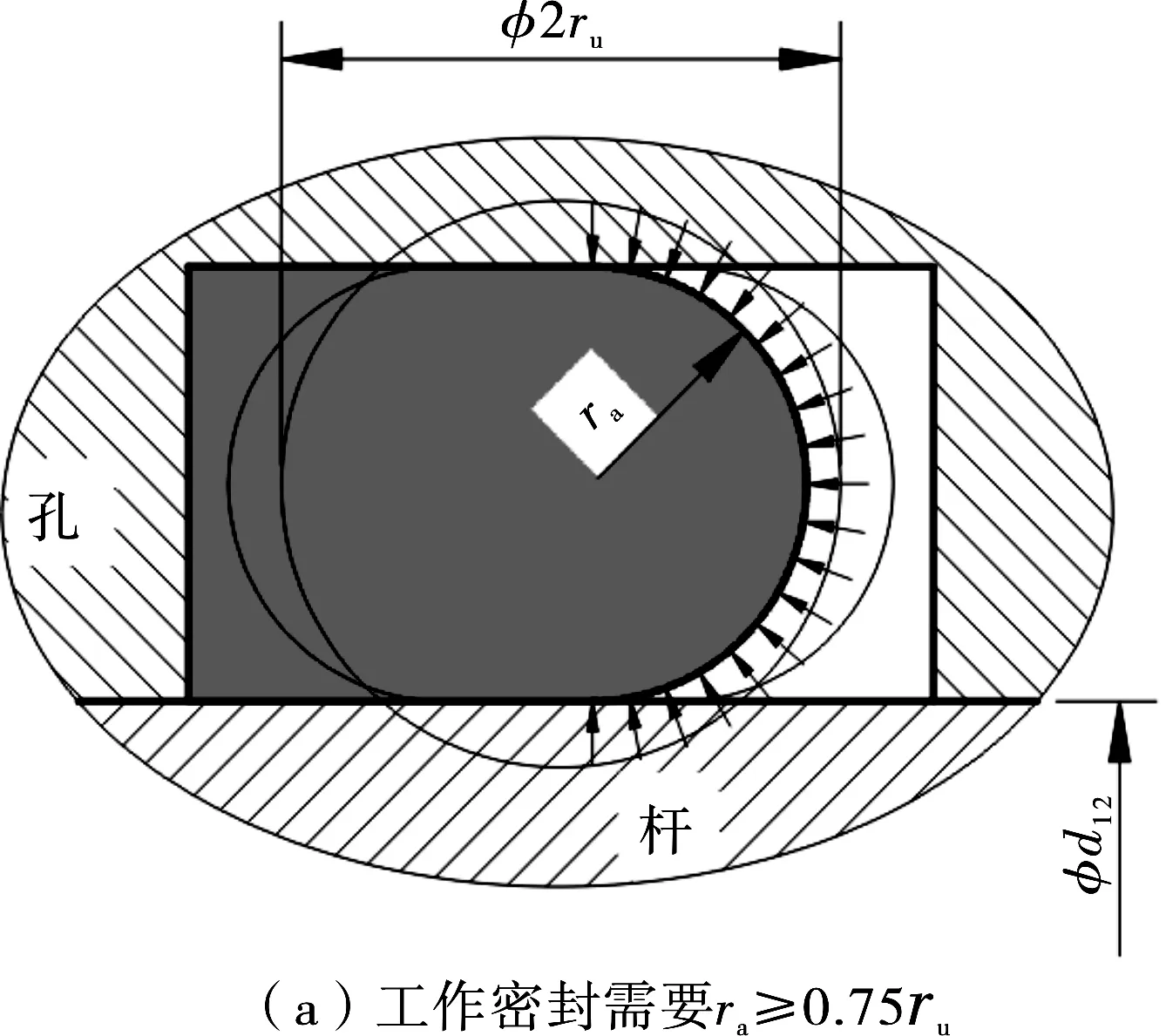
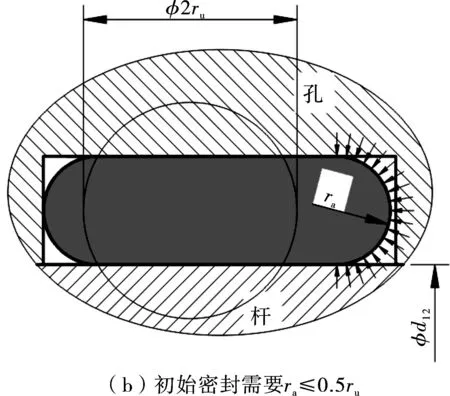
图14 矩形容腔只有一个固定不变的ra

图15 圆壁容腔的O形环密封

既然圆壁容腔中的无芯橡胶O形环只有一个既可致环的流动阻力至0又可致环的流动动力不断增加的流体挤压角，和一个可致环的密封应力不断增加的挤出角，即无任何消耗动力的其它多余流动，那么，任何可渗穿密封接触面而泄漏的初始流体压力，就可瞬间致O形环脱离其容腔圆壁而形成图15右侧所示的结构，开启其由大空间至小空间的移动密封进程。由于微弱流体压力下的无芯橡胶O形环还有明确的固性行为，因此，可以将图15右侧结构视为大-小端塞结构，可将大端面上的微弱流体压力放大为小端接触面上的不小于环材极限强度的密封应力，从而致圆壁容腔中的O形环不再需要通过安装实现初始密封。所以，基于容腔多边形内切圆的基圆制O形环密封是最科学的，详细论述参见文献[8，15]。

5 矩形环密封的应用场合

矩形环密封见图16。图中r为致环端楔动的弹性变形旋转半径，h为环容腔深度(环安装后的受压高度)，h1为环尖底间的高度，h2为环尖顶间的高度，do为被连管的公称外径，b为环的公称壁厚。对接特设端上径向内凸的环容腔缚壁，可给安装中因泊松变形而于中部紧触缚壁的自紧密环，同时提供一个以r为半径的弹性转动变形支点和2个泊松补偿角(θx)。因此，在密封连接系统中，只要自紧密环在压力作用下能首先变形，则任何流体压力都既可致未屈服的自紧密环按2个刚性楔工作，又可致已屈服的自紧密环按2个柔韧材团工作，或都能致自紧密环至充分自紧密接触。

图16 矩形环密封

由于自紧密环的矩形截面两端按环尖底间高度h1<环容腔深度h<环尖顶间的高度h2向外渐尖设计，使有压碎环端面潜能的紧固件也无压屈服环体的机会，从而绝对确保环的密封难至系数m1<1，而压缩成一层薄膜的环端部又有逼近无穷大的抗压强度而可绝对确保环端面无压缩破损，因此，任何适度按螺栓总抗拉能力/面积>管的抗拉能力/面积>环体截面积>环端面积设计的螺栓连接，都能确保：①比被连接管更抗拉的紧固件有同时致环端充分塑性变形和环体充分弹性变形的条件。②在装配和工作中，首先更多发生的是环的密封变形而非其它零部件的任何其它变形，以至于当环按k>1+b/d1r设计而确保其密封作用力Fs大于其去密封作用力Fu时，在选择脂/剂、微观锯齿环和O形环或矩形环中的1种、2种或3种作密封元的并有充分周向均匀压紧保障的任何螺栓连接中，永远都不会有密封所致的失效。

此外，矩形环还可用与压力容器体相同的材料制造而不再受材料的工作压力、温度、热胀冷缩系数、腐蚀性和制造技术的限制，因此，矩形环密封是非常理想的面密封，详见文献[8]。

6 三角形环密封的应用场合

大小规格升降阀杆柱密封结构分别见图17和图18。

1.阀体(杆壳) 2.反挤出C形环 3.硬压环 4.软密封环 5.单匝反挤出环 6.阀杆 7.压盖图17 小规格升降阀杆柱密封

1.阀体(杆壳) 2.反挤出C形环 3.硬压环 4.软密封环 5.单匝反挤出环 6.蝶形弹簧 7.六角螺钉 8.压盖 9.阀杆 10.球面垫圈 11. 硬压环(套)图18 大规格升降阀杆柱密封

无反挤出金属C形环的软三角形环的最大许可工作压力pmr等于其内切圆环的模拟金属O形环薄壁管在容腔中能够承受的极限压力，即pmr=0.5Rmrru/rc，其中rc为软环在离杆角的挤出弧半径，ru为基准三角形的内切圆半径。而有反挤出金属C形环的软三角形环的最大许可工作压力pmrc则为无反挤出金属C形环的软三角形环和反挤出金属C形环分别能够承受的极限压力之和，即pmrc=0.5Rmrru/rc+Rmcδc/rc，其中δc为反挤出金属C形环的壁厚，Rmc为反挤出金属C形环的抗拉强度。

7 结语

实现初始紧密连接需要加载其密封面至无丝毫抗拉的程度，即至其密封应力不小于密封面材料极限强度的程度，因此，必须致密封元被压缩成薄膜或者受封闭压缩，即必须确保受压密封元没有泊松变形和具有足够的挤出强度，以确保密封元在最大工作压力下都不发生任何的压缩和拉伸破损。维持初始紧密连接需要进一步加载其密封面或者密封元达到其密封应力不小于流体压力的程度。实现和维持初始紧密连接往往都要求密封元能够正交传递压力，将加载压力有效转换为与加载压力垂直的密封应力。

泊松比是物质的液性行为指数，而且泊松比越趋近0.5的物质越具有充分的液性行为和不可压缩性而越能有效瞬间实施压力的正交转换。材料的泊松比不仅随着温度和加载压力而变化，而且是滞后加载压力变化的。流体压力和活动杆所需的密封应力都是不断变化的。因此，实现和维持充分紧密连接必须确保其密封元时刻都能有0.5比的泊松变形能力，以便能将加载压力有效瞬间正交转换为密封应力。

泊松比是物质的非加载方向与加载方向的应变比，如果容腔有角度不小于θe=arctan(h/d)的致受压密封环由大至小的移动空间，则在大空间，具备与不具备0.5比泊松变形能力的各环层在压入小空间瞬间，都具有0.5比的泊松变形能力，等同于确保密封环时刻都有0.5比的泊松变形能力。

工作中具备0.5比的泊松变形能力的密封元都是受约束压缩的，除了在挤出角里有宏观拉伸应变之外，再无其它任何宏观拉伸和压缩松应变，因此，其最大工作压力是由其在挤出角的极限抗拉能力决定的，并且已经为橡胶O形环密封的高压应用史所充分证实。

参考文献：

[1] 徐长祥，张晓忠，陈佑军.徐氏流体密封与流动理论论文专集[C].纽约：科学出版集团，2016. http://www.sciencepublishinggroup.com/specialissue/164024.

XU C X，ZHANG X Z，CHEN Y J. The special issue of Xu’s sealing and flowing theories of fluids[C]. New York：Science Publishing Group，2016.http://www.sciencepublishinggroup.com/specialissue/164024.

[2] Greaves G N，Greer A L，Lakes R S，et al. Poisson’s ratio and modern materials[J]. Nature materials，2011，10：823-837.

[3] 何曼君，张红东，陈维孝，等.高分子物理[M].上海：复旦大学出版社，2006：106-107.

HE M J，ZHANG H D，CHEN W X，et al. Polymer physics[M]. Shanghai：Fudan University Press，2006：106-107.

[4] Polymer Science Learning Center. Rubber and rubberiness，level three，the macrogalleria of polymers and polymer science[Z]. USA：the University of Southern Mississippi，2005. http：//www.pslc.ws/macrog/level3.htm.

[5] Koh-hei Nitta，Masahiro Yamana. Poisson’s ratio and mechanical nonlinearity under tensile deformation in crystalline polymers[M]. London：InTech，2012：113-132.http：//www.intechopen.com/books/rheology/poisson-s-ratio-and-mechanical-nonlinearity-undertensile-Deformation.

[6] 丁发兴，余志武，温海林.高温后Q235钢材力学性能试验研究[J].建筑材料学报，2006，9(2)：245-249.

DING F X，YU Z W，WEN H L. Experimental research on mechanical properties of Q235 steel after high temperature treatment[J]. Journal of building materials，2006，9(2)：245-249.

[7] Parker Hannifin Corporation. Parker O-ring handbook ORD 5700(Fig.3-8 O-ring leak rate：3-19)[Z]. Cleveland USA，2007. http：//www.parker.com/literature/ORD%205700%20Parker_O-Ring_Handbook.pdf.

[8] 徐长祥.徐氏密封理论与矩形和O形环密封[J].石油化工设备，2013，42(2)：75-85.

XU C X. XU’s sealing theory and rectangular & O-shaped ring seals[J]. Petro-chemical equipment，2013，42(2)：75-85.

[9] Rules for bolted flange connections with ring type gaskets：ASME Boiler and Pressure Vessel Code，Section VIII，Division 1，Appendix 2[S].

[10] 徐长祥.密封紧密度的定义、量化和测定[J].石油化工设备，2014，43(3)：11-14.

XU C X. Definition，quantifying and gauging of tightness[J]. Petro-chemical equipment，2014，43(3)：11-14.

[11] 徐长祥，张晓忠，陈佑军.流体的压力能与漏阻、流阻和流抗[J].液压气动与密封，2015，35(9)：4-10.

XU C X，ZHANG X Z，CHEN Y J. Pressure energy，resistance and reactance in leak and flow of fluids[J]. Hydraulics pneumatics & seals，2015，35(9)：4-10.

[12] Mechanics of Materials Laboratory. Time dependent behavior：creep，ME 354[M]. USA：the University of Washington，2007.

[13] Lakes R S. On Poisson’s ratio in linearly viscoelastic solids[J]. J Elasticity，2006，85：45-63.

[14] Rod Lakes. Meaning of Poisson’s ratio[DB/OL].http：//silver.neep.wisc.edu/～lakes/PoissonIntro.html.

[15] 徐长祥，张晓忠，陈佑军.必须废除所有国际密封基础标准[J].石油化工设备，2016，45(4)：40-50.

XU C X，ZHANG X Z，CHEN Y J. It is necessary to abrogate all the international basic standards of seals[J]. Petro-chemical equipment，2016，45(4)：40-50.

[16] Niels A. Christensen. Packing：US 2180795[P].1939-11-21.

[17] Fluid power system-O-rings—Part 2：Housing dimensions for general applications：ISO 3601-2：2008[S].

[18] Parker Hannifin Corporation. Parker O-ring handbook ORD 5700(Figs.1-4 to 1-7：1-3)[Z]. Cleveland USA，2007. http：//www.parker.com/literature/ORD%205700%20Parker_O-Ring_Handbook.pdf.