一类非线性积分微分方程的全局吸引子
2018-05-30柴玉珍
张 珊,柴玉珍
(太原理工大学 数学学院,太原 030024)
积分微分方程是多年来被国内外学者所关注的非线性演化方程,许多数学物理问题需通过积分微分方程求解。积分微分方程是近代数学的一个重要分支。数学、自然科学和工程技术领域中的许多问题都可以归结为积分微分方程问题。正是因为这种双向联系和深入的特点,积分微分方程论得到了迅速地发展,成为包括众多研究方向的数学分支。
起初在文章[1-3]对线性积分微分系统进行过描述和研究,之后文章[4-5]开始对非线性的积分微分方程进行研究,研究其解的初边值问题和收敛性等。近几年,人们开始研究该类方程的吸引子问题[6-9]。
本文研究如下初边值问题:
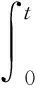
(1)

方程(1)当h(·)=g(·)=0时用于表示非线性弹性杆和弱非线性效应的空间变换离子声波纵向波传播的问题[10-11]。对于经典波动方程的全局吸引子存在性已有广泛的研究,在[12-14]这些参考文献中,作者经常把经典波动方程转化为下列系统:
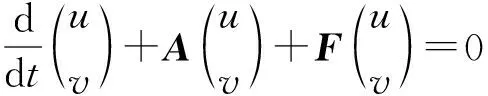
(2)
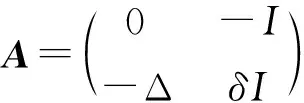
根据经典半群理论,可得全局吸引子的存在性。但对于方程中含有耗散项Δutt和积分项的方程[6-9],它不同于一般的波动方程,因此我们不可能直接把它化为式(2),也不能用经典半群理论来研究这类方程的全局吸引子。故在本文试图用ω-极限紧的方法证明系统(1)解的全局吸引子的存在性,其次本文使用一种新的方法引理2.2,证明了半群{S(t)}t≥0在D(A)×D(A)中的耗散特性,而在此之前的大部分文献一般使用Gronwall不等式得到半群的耗散特性,另外本文所讨论的方程类型更加广泛,所以在一定程度上对文献有所推广。
1 预备知识
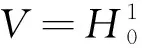
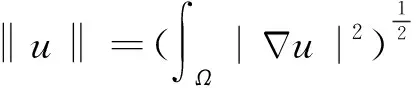
Lp(Ω)(3≤p≤∞)上的模记为
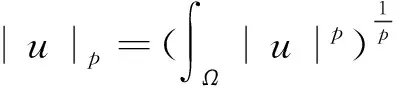
且V和H上的内积分别记为
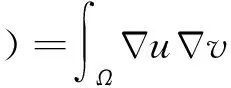

记Hilbert空间上的积为E0=V×V,E1=D(A)×D(A),且记无论同一行还是不同行的C均为常数。
本文中对f,h,g,k,ψ做了如下假设:
I1)

即
f'(s)≥-β, ∀s∈R.
(3)
|f"(s)|≤C(1+|s|3), ∀s∈R.
(4)
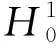
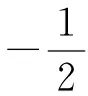
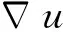
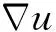
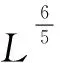
使得
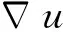
且满足下述
hi(x,t)(0≤i≤4)在Ω×R+关于时间变量有一阶偏导数且满足
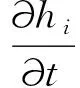
(5)
I3)对任意的k∈W1,∞(0,∞)∩W1,1(0,∞),k(t)≥0,kt(t)≤0,∀t≥0,
1) -m0k(t)≤kt(t)≤-m1k(t),∀t≥t0,
2)k(0)=0,|kt(t)|≤m2k(t),∀t∈[0,t0],
3)
0≤ktt(t)≤m3k(t),∀t≥0,
4)

(6)
I4)ψ(s,q)在R1×R1上有二阶偏导数,且各二阶偏导数都在有界集上
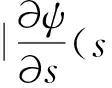
(7)
下面,概括一下关于吸引子存在性的一些具体结论。
定义1[15]Banach空间X上的半群{S(t)}t≥0称满足条件(C),如果对X中的任一有界集B和任意的ε>0,存在tB≥0和X中的有限维子空间X1,使得对任意的t≥tB,都有{PS(t)x|x∈B,t≥tB}有界,且
‖(I-P)S(t)x‖X<ε,∀t≥tB,x∈B.
其中,P:X→X1是有界映射,I是恒等映射。
引理1[15]设X是Banach空间,{S(t)}t≥0是X上的C0半群,如果{S(t)}t≥0满足如下条件:
1) {S(t)}t≥0在X中有有界吸收集B0;
2) {S(t)}t≥0在X中满足条件(C);
则{S(t)}t≥0在X中有全局吸引子。
引理2 已知Φ(t)(t∈R+)是绝对连续的正值函数,且存在ε>0使得微分不等式

成立。其中存在α≥0和a∈[0,1),使得q(t)满足
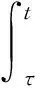
存在β≥0,使得p(t)满足
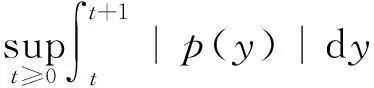
α,β是与t无关的常数。则存在T=T(α,β),使得t≥T时
Φ(t)≤ρ.
其中ρ=ρ(ε,a,α,β)是一个正常数。
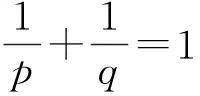
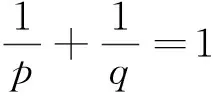
2 D(A)×D(A)上的全局吸引子
定理2 设假设I1)-I4)成立,σ,u0,u1是给定的函数且满足
σ∈H,u0∈D(A),u1∈D(A) .
则方程(1)存在唯一的解
u,ut∈C([0,T];D(A)),utt∈L∞([0,T];D(A)).
且(u,ut)在E1中对初值具有连续依赖性。
由定理2可以定义E1上的一个C0半群{S(t)}t≥0,
在法律完善的条件下如何让教师使用《教师法》来维护自己的合法权益成为当务之急。增强教师权利意识成为关键。首先,可以加大宣传力度,综合运用各种传播渠道如:网络、电视、新媒体等多种方式宣传《教师法》,扩大《教师法》的影响力。除此以外,可以定期组织教师培训宣传,讲解《教师法》的相关内容,让教师充分了解《教师法》并学会运用它维护自己的权利。
S(t):E1→E1,S(t):(u0,u1)→(u,ut).
2.1 有界吸收集
利用引理的方法并结合定理2可以得到下列结论。
定理3 {S(t)}t≥0在E1中有有界吸收集B0,即对任意的有界集B∈E1,存在t0=t0(B),使得
S(t)B⊂B0,∀t≥t0.
证明:设
|Δu0|2+|Δu1|2≤R,(R>0).
方程(1)和ut在L2上作内积,再在[0,t)上积分,得
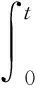
(8)
设v=ut+δu,方程(1)化为下列形式:
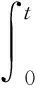
(9)
用-Δv和式(9)在L2(Ω)上作内积,经过计算,得
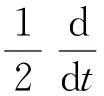
(10)
对上式右端利用变上限积分和分部积分公式以及根据I2)得:
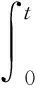
(11)
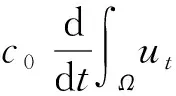
(12)
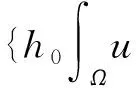
(13)
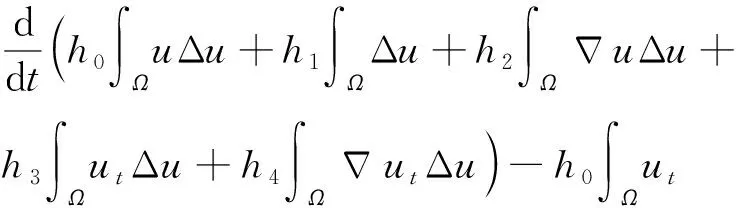
(14)
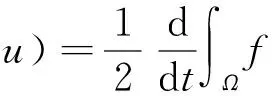
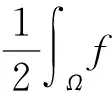
(15)
将式(11)-(15)代入式(10)可得
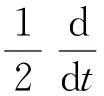
(16)
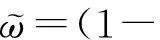
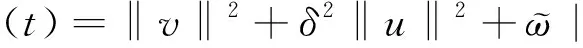
(17)
则式(16)可改写为

(18)
由Sobolev嵌入定理和引理3、4得:
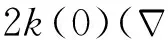
≤C(‖u‖|Δu|+|Δu|2)≤C|Δu|2.
(19)
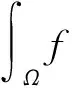
C1‖ut‖|Δu|2+C2‖u‖3‖ut‖|Δu|2.
(20)
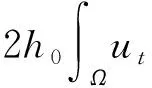
(21)
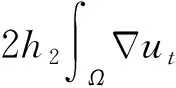
(22)
将式(19)-(22)代入式(18)并利用式(6)可得

(23)
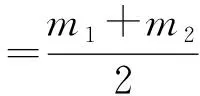

设
q(t)=2
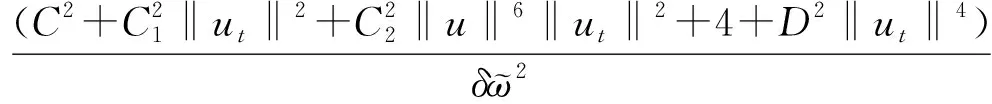
则
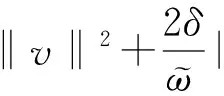
则式(17)可写为

其中,
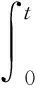
Φ(t)≤ρ.
其中,ρ=ρ(δ,α,β)是一个正常数。即
‖ut‖2+γ|Δu|2+ω|Δut|2≤ρ.
故B0={(u,ut)T∈E1|‖ut‖2+γ|Δu|2+ω|Δut|2≤ρ}是{S(t)}t≥0在E1中的有界吸收集。
注1:对于假设(I2)当hi(x,t)关于时间变量一阶不可导时上述结论也成立。
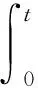
注3:(由引理2、3):
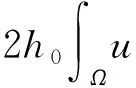
2.2 ω-极限紧和全局吸引子
为了方便,假定B是E1的任意有界的子集。
定理4 半群{S(t)}t≥0在E1中是ω-极限紧的,即对任意的ε>0,存在T=T(B),N=N(B)(有限维子空间Hm的维数),当任意t≥T,m≥N,(u0,u1)∈B时,有
‖v2‖2+γ|Δu2|2+ω|Δv2|2<ε.
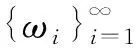
0<λ1<λ2<…<,λm→∞,当m→∞ .
设Hm=span{ω1,ω2,…,ωm},可以将它唯一的分解为
u=u1+u2,
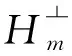
用式(9)的方程在L2(Ω)上和-Δv2作内积
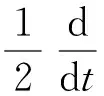
(24)
应用Sobolev不等式和定理3,对任意的ε>0,存在T=T(B,ε),N=N(B)(有限维子空间X1的维数),当任意的t≥T,m≥N,(u0,u1)∈B时,有
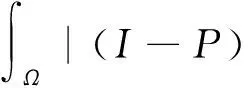
则
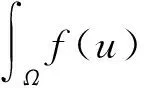
则式(24)变为
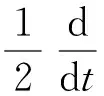
由Gronwall不等式,对任意的t≥T,m≥N,(u0,u1)∈B,有
‖v2‖2+γ|Δu2|2+ω|Δv2|2≤Cε.
其中C是与ε无关的常数。
由定理3,定理4和引理2可得到下面结论:
定理5 设具有光滑边界的有界区域Ω∈R3,且假设I1)-I4)成立,则半群群{S(t)}t≥0在E1中存在全局吸引子Λ.
:
[1] BURTON T A.Volterra integral and differential equations[J].Academic Press,1983,27(1):104-105.
[2] KOLMANOVSKII V B,NOSOV V R.Stability of functional differential equations[J].Academic,1986,6(9):90.
[3] GOPALSAMY K.Equations of mathematical ecology[J].Parti Autonomous Systems,1990.
[4] CUI S B.Initial-boundary value problems for semilinear hyperbolic convolutional integrodifferential equations[J].Acta Mathematicae Applicatae Sinica,1988,11(3):271-286.
[5] WU Z Q,SHI D W.Convergence analysis for nonlinear integro-differential equations with a weakly singular kernel[J].Polski Tygodnik Lekarski,2012,47(8):8.
[6] LIANG F,GUO Z.Asymptotic behavior for second order stochastic evolution equations with memory[J].J Math Anal Appl,2014,419(2):1333-1350.
[7] CAVALCANTI M M,FATORI L H,MA T F.Attractors for wave equations with degenerate memory[J].J Differential Equations,2016,260(1):56-83.
[8] ZHOU S,ZHAO M.Random attractors for damped non-autonamous wave equations with memory and white noise[J].Nonlinear Anal,2015,120:202-226.
[9] XIE Y,ZHONG C.Asymptotic behavior of a class of nonlinear evolution equations[J].Nonlinear Anal,2009,71(11):5095-5105.
[10] SEYLER C E,FANSTERMACHER D L.A symmetric regularized-long-wave equation[J].Phys Fluids,1984,27(1):4-7.
[11] CLARKSON P A,LEVEQUE R J,RALPH S.Solitary-wave interaction in elastic rods[J].Stud Appl Math,1986,75(2):95-123.
[12] PATA V,SQUASSINA M.On the strongly damped wave equation[J].Comm Math Phys,2005,253(3):511-533.
[13] PATA V,ZELIK S.Smooth attractors for strongly wave equations[J].Nonlinearity,2006,19(7):1494-1506.
[14] LI K,WEI H.An attractor for the singularly perturbed Kirchhoff equation with supercritical nonlinearity[J].J Math Anal Appl,2014,411(1):240-253.
[15] MA Q F,WANG S H,ZHONG C K.Necessary and sufficient conditions for existence of global attractors for semigroups and applications[J].J Indiana Univ Math J,2002,51(6):1541-1559.
[16] 王术.Sobolev空间与偏微分方程引论[M].北京:科学出版社,2009.
