一道向量题的多种解法探究

江苏省常州高级中学 (213003) 陈 武

题面设置简单、解题入口宽、解法灵活多样，能有效地考查平面向量的基础知识，考查数形结合思想和转化化归的能力以及综合运用所学知识分析问题和解决问题的能力.下面对这道题目的解法进行探究，供读者参考.

图1

解法1:建立直角坐标系xOy如图1所示，不妨设A(-1，0),B(1,0),C(cosα,sinα)，P(rcosθ,rsinθ)其中r∈[0,1],α,θ∈[0,2π].

4(cos(α-θ)=-1，r=1时等号成立);

评注:本解法通过建立直角坐标系xOy用向量数量积的坐标运算来求解，思路清晰.在求解3r2-2rcos(α-θ)-1的最值时先 “固定”r处理cos(α-θ)，然后再求解最大最小值.

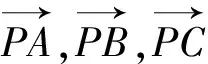
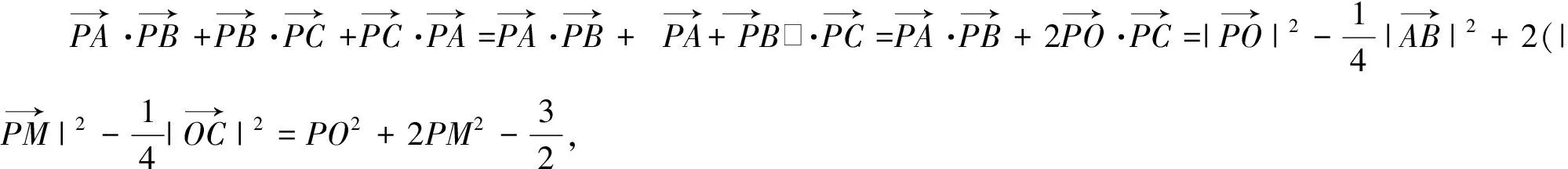
文[1]给出矩形的如下性质

设O为矩形ABCD所在平面上任意一点，则恒有OA2+OC2=OB2+OD2.

评注:(1)本解法中运用了矩形的这个看似简单但功能强大的性质，转化为求2PO2+PC2-2的取值范围；(2)2PO2+PC2-2取值范围的求解也可利用解法3的不等式和数形结合思想来处理.

[1]王淼生.在谈矩形一个性质得应用[J].数学通讯(上半月)，2016(7、8)：53-55.

[2]袁青.巧用极化恒等式解决两类平面向量数量积问题[J]. 数学通讯(上半月)，2016(7、8)：24-25.