高速铁路引入客运走廊的交通结构预测

陈 晖

(嘉兴市铁路建设管理办公室，浙江嘉兴 314000)

随着国内重要城市间高速铁路系统的不断发展，不仅为人们出行提供了极大便利，带来了人们生活方式的改变，而且大大提高了铁路客运能力，缓解了铁路运输的压力，在带来上述变化的同时，也给原有的客运交通系统带来一定程度的冲击。在一般情况下，客运通道内的各种交通方式间存在竞合关系，其基本属性大体上决定了各自的客流吸引群体，从而形成相对稳定的客运交通结构，犹如一个“生态系统”[1]。当高速铁路交通方式引入时，“生态系统”的相对平衡就会被打破，系统内各种交通方式的吸引对象会重新进行调整而达到新的平衡。因此，在高速铁路快速发展的今天，进行高速铁路引入客运走廊后交通结构的预测研究，优化配置客运通道内的各种交通资源，形成合理的客运交通结构就显得尤为重要。

1 交通方式结构预测研究现状

在进行交通方式结构预测时，以离散选择模型为代表的非集计模型(如Logit模型)被广泛使用[2]。离散选择模型既可以用于阶段性选择，也可用于多阶段同时性选择，是一个较有弹性的模型。该模型不仅用于解决传统四阶段法的内在问题，还可对决策结构进行优化组合(如图1所示)。

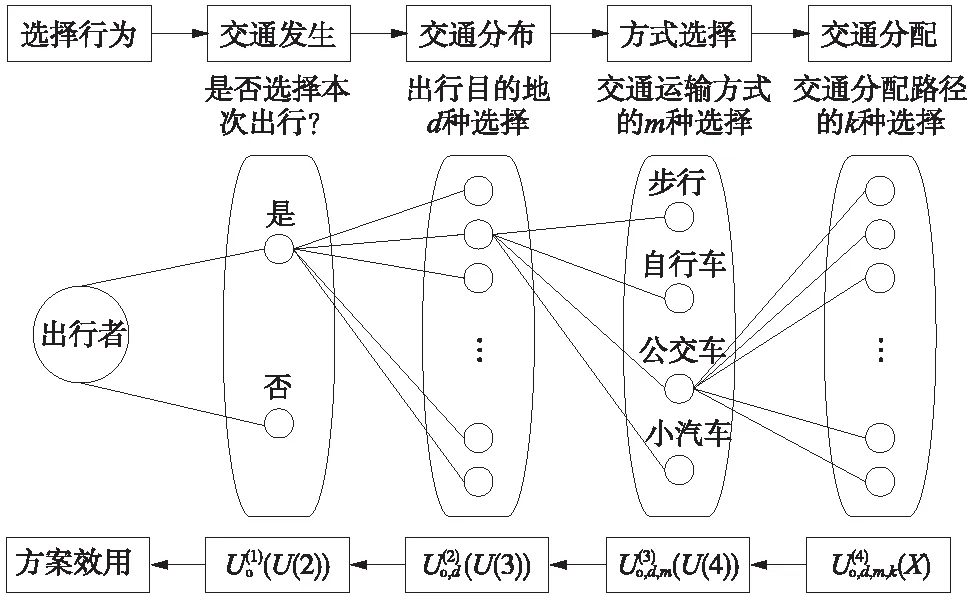
图1 离散选择模型应用于传统四阶段法

离散选择模型的最大优势在于可以处理新引入交通方式的情形，适合短期交通结构的预测，同时可以考察不同政策参量的敏感性，是目前交通行为学和需求预测研究的一个热点。Koppelman提出了增量Logit模型的概念[3]，主要是利用现有交通方式数据资料来预测某种新交通方式引入后的交通需求变化情况。为解决意向调查数据与实际选择间常有较大误差的问题，Ben-Akiva & Morikawa利用实际调查数据和意向叙述[4]，建立预测交通方式转移率的模型。Hibrobata & Kawakami以意向调查方法收集相关基础资料[5]，分析日本名古屋地区城市轨道交通服务水平改变后，小汽车出行者转移到轨道交通方式出行的选择行为。Fowkes & Preston为预测英国Leicester至Burton间新铁路的客运服务需求[6]，同样以意向调查方法收集出行者选择新铁路运输方式的意向数据。一般情况下，如直接询问出行者是否愿意选择新铁路运输系统，收集的意向数据可能会产生高估的情况。针对这一情况，该研究考虑设计仿真的意境组合，让出行者做出假设性的选择，以求得各属性的极限值，当属性超过此极限值时，出行者将会改变出行计划而选择新的交通方式。

总的来说，国外对离散选择模型的研究注重理论分析和模型改良，大都用于探讨某种旅行目的的交通方式选择行为，但当出现新的交通方式后，少有文献报道研究如何通过客运交通方式结构的调整预测来进行相应交通政策的制定。通过客运交通方式结构预测分析模型，可以制定合理的交通政策和管理措施，从而调整和引导交通方式结构，这是有关部门更为关注的焦点。

2 交通方式结构预测的离散选择模型

离散选择模型的两大基石是行为选择理论和随机最大效用理论，推导过程如下：

(1)出行者n，将在J种交通方式当中进行选择，无论选择哪一种都能获得一定的效用。出行者n从选择项j中获得的效用可以用Unj表示，其中j=1，…，J。

(2)由于出行者进行的是效用最大化的选择，因此效用行为模型可以表示成当出行者n选择项i，仅当Uni>Unj，(∀j≠i)时效用最大。

根据上述的两个假设条件，效用可以分解成效用确定项和随机项两部分

Unj=Vnj+εnj

(1)

式(1)中，Vnj为效用项的可观测部分，εnj为效用项中不可观测部分，有

Unj=Vnj+εnj∀j，那么对于Un1，其概率P(Un1>Un2)的值为

等的时间总是充满无聊，但又别无他法。常爱兰叫周小羽干活，比如刷碗，比如洗菜，周小羽是一样也不肯干的。他的成绩很差，语文勉强及格，数学也是勉强及格。所以，常爱兰经常说，你这个天杀的，你老爸好的不像坏的全像来了。

Pn1=P(Un1>Un2)=P(Vn1+εn1>Vn2+εn2)=

(2)

即f(y，z)为ε1，ε2的联合概率密度函数。

假设任一εnj服从Gumbel分布，且其中ε1，ε2相互独立并服从二重指数分布，即

F(y)=exp[-exp(-by)]，f(y)=bF(y)exp(-by)

(3)

则

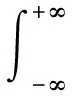
(4)

(5)

3 交通方式结构预测建模构思

3.1 建模时序划分

根据个体对交通方式的选择可划分为如下三个阶段：①新交通方式运营前期的稳定状态。在该状态下意味着出行者对客运交通方式选择已经达到比较稳定的状态，即已产生习惯性的交通方式选择行为。②新交通方式运营初期的扰动状态。所谓扰动状态是指出行者在选择客运交通方式出行时尚未产生习惯性的行为，此时出行者对于整个客运交通系统还处在适应和学习的阶段。③新交通方式运营成熟期的稳定状态。随着出行者对于当前客运交通市场的适应与熟悉，找到习惯交通出行方式后，重新回到运营前的稳定状态。

运营前期的稳定状态下，新交通方式尚未引入，出行者仍按习惯选择交通方式出行，具有相对稳定性；运营初期的扰动状态下，新交通方式加入客运系统，使得出行者有了新的交通方式选择，但绝大多数个体者存在猎奇的非理性因素，会尝试使用新的交通出行方式，此时的交通方式选择行为尚不稳定。在尝试使用新交通方式出行的过程当中，根据经验和自身的判断，有些出行者转向新交通方式，有些出行者则仍旧使用原来的交通方式，最终也将达到稳定的状态，此时称为新的交通方式运营后的稳定状态。在扰动期，交通方式选择行为具有暂时性，在一般研究过程中并不加以细分，而是着力于高速铁路运营前后稳定状态下个体选择行为的研究。

3.2 建模思路分析

基于图2所示的建模思路，拟通过以下6个步骤来建立较精确的预测模型。

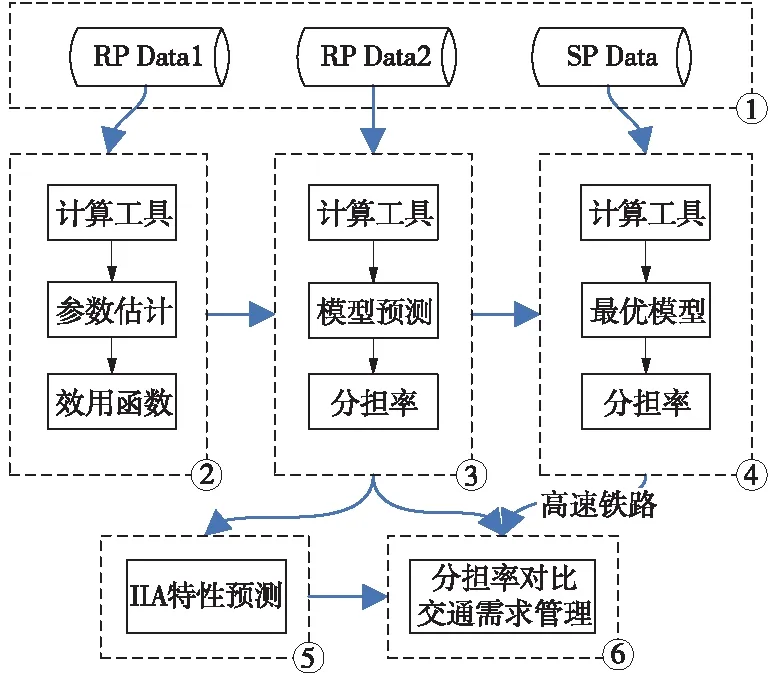
图2 建模思路流程及关系

(1)高速铁路对于很多城市而言是一种新型的交通出行方式，无法通过现状的交通调查和现状的交通系统来判断高速铁路引入后给客运交通系统带来的影响。可以采用RP(Revealed Preference)和SP(Stated Preference)相结合的方法来进行出行者的意向调查。一方面完成现状数据的采集，即RP调查部分；另一方面对假定条件下出行者的意向偏好进行调查，即SP调查部分。考虑模型评价的精度和新交通方式的引入，可将调查数据分为3个部分：RP Data1、RP Data2和SP Data。其中，RP Data1主要用于各类模型参数的标定；RP Data2用于模型精度的评价和最优模型的确定；SP Data主要用于考察新交通方式引入后的交通方式结构预测。

(2)从调查数据当中随机抽取一定数量的样本形成RP Data1，利用离散选择模型计算工具(如Biogeme)对不同模型的参数进行估计，形成不同模型的效用项描述。对个体出行者而言，方式选择的改变不是由于方式选择和效用函数之间关系发生了改变，而是相关的变量属性本身发生了变化。

(3)根据步骤2得到的不同类别离散选择模型的效用函数，并结合RP Data2(完整的调查样本)，利用计算软件(如Biosim)进行分担率的仿真训练，求得不同效用函数下各种交通方式的分担率，并与RP Data2实际的分担率进行比较，选定最优模型，为交通方式结构预测奠定模型基础。

(4)步骤4所进行的工作与步骤2相似，不同的是模型为最优模型，参数标定数据变成了SP Data。由于RP数据具有可靠性而SP数据在调查过程当中更具灵活性，可建立RP/SP联合数据来进行交通结构的预测，目的是得到新交通方式引入后的分担率。

(5)利用IIA(Independence from Irrelevant Alternation)特性可以进行高速铁路影响下客运通道内的交通结构预测。

(6)将步骤3～步骤5三个环节当中的交通结构预测值进行对比分析，从而得到不同数据条件下交通结构的变化情况，并利用模型当中的政策参数进行敏感性分析，制定相应的交通管理措施。

3.3 模型变量选择

由于出行者个体喜好等不可测因素的影响，在面临选择项相同的情况下，出行个体不一定作出相同的选择，离散选择模型中各选择项的效用是一个随机变量

Vnj=β1xn1+β2xn2+…+βKxnk=β'xn

(6)

其中：xn=(xn1，xn2，…，xnk)′为特征参数向量；β=(β1，β2，…，βK)′为待估参数向量。

特征变量的个数越多，模型求解的过程就越复杂。由式(6)可知，选择概率只与效用差有关。根据这一原则，可对变量进行分类，减少待估计参数数量，从而降低模型求解的难度，提高模型的计算效率。影响居民出行交通方式选择的主要因素相当复杂，但一般可以划分为个人属性变量、选择项属性变量和常变量三类。

性别、年龄、职业、家庭总收入、小汽车数量等因素均包含在个人属性之中；而选择项属性则主要包括出行目的、出行时间、出行费用、换乘次数、公交聚集时间、公交等待时间和小汽车停车费用等。Mcfadden早在1976年就研究了离散选择模型当中各模型变量的解释能力，进一步证明了交通方式选择与出行个体属性之间的相互关系[7](见表1)。

表1 离散选择模型变量解释能力

调查所获得的出行时间及出行费用数据包含了出行者对出行时间及出行费用的理性思考与感性认识，而个体对交通方式的选择正是建立在个体对时间、费用认知基础之上，尽管存在偏差，但却是个体选择某种交通方式的重要原因。

4 结束语

以离散选择理论为主线，提出高速铁路引入客运走廊后的交通结构预测研究思路，分析出行者选择不同客运交通方式时的行为特性和影响因素。在此基础上，探讨高速铁路引入前后交通方式之间的客流转移情况，量化高速铁路运营后的影响，进而选择有效的交通需求管理措施，优化交通方式结构配置。

[1] 陆振波，黄卫，王树盛.大容量快速公交系统模式与规划选择方法研究[J].土木工程学报，2008，41(6)：104-107

[2] 关宏志.非集计模型：交通行为分析的工具[M].北京：人民交通出版社，2004

[3] Koppelman F S. Predicting Transit Ridership in Response to Transit Service Change[J]. Journal of Transportation Engineering， 1983(109)：88-98

[4] Ben-Akiva M，Morikawa T. Estimating of Switching Models from Revealed Preferences and Stated Intention[J]. Transportation Research， 1990(24A)：485-495

[5] Hibrobata Y， Kawakami S. Modeling Disaggregate Behavioral Modal Switching Models Based on Intention Data[J]. Transportation Research， 1991(24B)：15-25

[6] Fowkes T， Preston J. Novel Approaches to Forecasting the Demand for New Local Rail Service[J]. Transportation Research， 1991(25A)：102-115

[7] Train K， McFadden D. An Application of Diagnostic Tests for the Independence from Irrelevant Alternatives[J]. Transportation Research Record， 1976(637)：39-46