基于圆弧啮合线内啮合齿轮设计与特性分析
2018-05-30王延忠李圆任少英赵鹏坤
王延忠,李圆,任少英,赵鹏坤
基于圆弧啮合线内啮合齿轮设计与特性分析
王延忠,李圆,任少英,赵鹏坤
(北京航空航天大学 机械工程及自动化学院,北京,100191)
针对内啮合齿轮传动,提出1种基于圆弧啮合线的大重合度内啮合齿轮构造方法。选取连接外齿轮和内齿圈节圆交点和齿顶圆交点的圆弧为啮合线,构造在该啮合线上共轭的外齿轮和内齿圈齿顶齿廓;根据共轭原理设计与齿顶齿廓共轭的齿根齿廓,完成内齿圈齿根齿廓修形;对新齿形进行根切检验,分析新齿形啮合几何特性及加载接触;利用数控加工方法完成内啮合齿轮样件的加工并进行啮合试验。研究结果表明:新齿形不产生根切和齿顶干涉;与渐开线内啮合齿轮相比,新齿形重合度大大提高,相对滑动率减小,相对法曲率增大;齿面接触和齿根弯曲应力显著降低,承载能力大大提高;齿数比为38/53的新齿形存在7对齿接触,验证了新齿形的大重合度啮合。
大重合度;内齿轮;啮合线;加载接触分析
内啮合齿轮作为齿轮传动重要部件之一,可传递相同方向的动力和运动,与外啮合齿轮相比,可降低由于共轭齿廓曲线相对滑动引起的动力损失,具有传动效率高、承载能力大等优点[1]。渐开线齿轮作为最重要的内啮合齿形,以其具有容易制造、互换性等优点获得了最广泛的应用。同时,渐开线齿形的啮合线为配对齿轮齿顶圆之间的一段线段,限制了重合度的提高。重合度是齿轮设计的重要指标之一,重合度提高可使更多轮齿分担载荷,从而降低单对轮齿负载,提高齿轮整体承载能力,降低传动噪声[2]。为获得大重合度齿轮,人们对渐开线齿形[3−4]、摆线齿形[5]进行改良,通过增大齿顶高、增大齿数或减小压力角[6−7]等方法实现大重合度啮合,但受制于渐开线、摆线的几何特性,这些改良方法在提高齿轮重合度的同时可能导致齿轮强度降低、啮合性能下降,因此,一些研究者从啮合原理出发,开发出了新型齿形。DONG 等[8]建立了根据啮合线构造共轭齿廓的数学模型,构造了直线啮合线、圆弧啮合线及二次曲线啮合线的圆柱齿轮和椭圆外啮合齿轮;王建等[9]以压力角为设计参数构造了啮合线,根据共轭原理构造齿轮齿廓并研究了压力角参数对重合度的影响,从而获得了大重合度齿轮设计参数。在内啮合齿轮方面,直线共轭内啮合齿轮在高端齿轮泵领域得到应用。魏伟锋等[10]利用齿廓法线反转法建立直线共轭齿廓参数化求解和分析方法,提出重叠干涉的判定条件及齿根、齿顶干涉的解决方案。相比于渐开线、摆线齿齿形,新型齿轮齿形复杂,缺少标准的加工工具,而高精度数控加工技术的发展为新齿形的加工制造及应用提供了条件。本文作者针对直齿内啮合齿轮传动,提出基于圆弧啮合线的大重合度内啮合齿轮设计方法。通过选择连接外齿轮和内齿轮节圆交点和齿顶圆交点的圆弧为啮合线,利用共轭原理,构造满足该圆弧啮合线的内啮合齿轮共轭齿廓及插齿齿条齿廓;研究新齿形的重合度、共轭齿廓相对滑动率及相对法曲率等几何特性,通过有限元加载接触分析研究齿轮的齿面接触强度、齿根弯曲强度;通过加工新齿形内啮合齿轮样件和啮合试验,完成重合度验证。
1 基于啮合线的内啮合齿轮共轭原理
在齿轮传动过程中,共轭齿轮以设计的传动比发生相对运动,随着接触点在啮合线上滑动,接触点在齿轮坐标系上划出的轨迹就形成了共轭齿廓曲线[11],因此,根据啮合线可以构造出满足在该啮合线上啮合的共轭齿廓曲线。外齿轮与内齿轮为1对共轭内啮合齿轮,假设其啮合线为01,根据该啮合线构造的外齿轮与内齿轮共轭齿廓曲线分别为1和2,c为与外齿轮齿廓1共轭的齿条齿廓。齿廓曲线1,2和c在啮合线上点接触,法向为。111,222和Xccc分别为与外齿轮、内齿轮、齿条固连的坐标系,fff为固定坐标系。当外齿轮和内齿轮分别绕中心1和2转过角位移1和2到位置1和2时,齿条沿轴平移距离到c位置,它们在节点f接触,且满足:

式中:1和2分别为外齿轮和内齿轮节圆半径。设啮合线01上点在坐标系fff中齐次坐标表达式为

式中:和为自变量。内啮合共轭齿廓曲线构造示意图如图1所示。
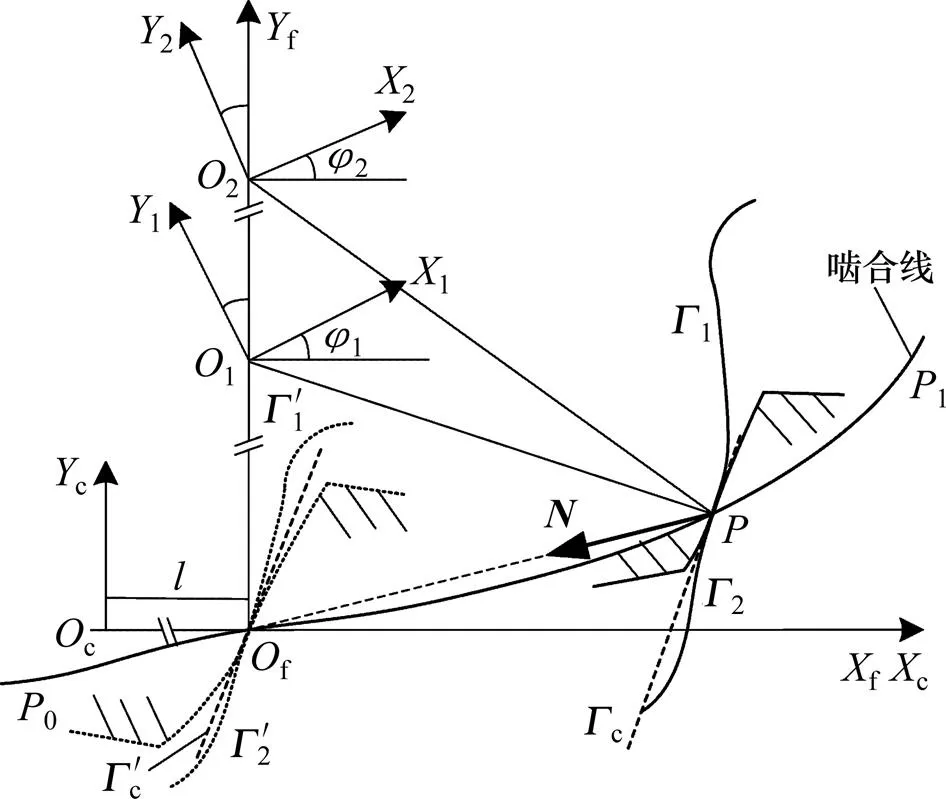
图1 内啮合共轭齿廓曲线构造示意图
通过坐标变换,分别得到外齿轮和内齿轮的共轭齿廓曲线1和2,其向量表示分别为1和2。

式中:1f和2f分别为坐标系fff到111和222的坐标变换矩阵。

根据平面齿轮啮合原理[12],共轭齿廓曲线在接触点的公法线通过瞬时回转中心,则共轭齿廓曲线在接触点处的法向量在fff上为

共轭齿廓曲线在接触点上的法向量1在111坐标中为

式中:1f为矩阵1f左上角2×2矩阵。根据齿轮啮合原理,啮合方程可表示为

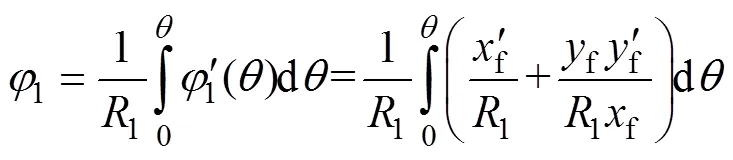
根据式(1)可得到内齿轮的角位移2。式(7)和(1)描述了啮合线上共轭点与外齿轮和内齿轮共轭齿廓上的齿形点之间的对应关系,因此,当已知啮合线方程式(2),将式(7)和(1)代入式(3)就得到了满足设计啮合线的外齿轮、内齿轮的共轭齿廓方程表达式。
2 圆弧啮合线及共轭齿廓
2.1 圆弧啮合线及齿顶齿廓
为提高内啮合齿轮的重合度,选择连接外齿轮和内齿轮节圆交点和齿顶圆交点的圆弧01为啮合线,圆弧啮合线构造如图2所示。与直线啮合线相比,圆弧啮合线大大增加了内啮合齿轮的重合度。根据几何原理,可求出圆弧的半径及弧度max,则圆弧啮合线在fff坐标系中的方程表达式为

将式(8)代入式(6),得到外齿轮角位移表达式

由于设计的圆弧啮合线位于齿轮的节圆和齿顶圆之间,构造的共轭齿廓曲线为齿顶到节点的齿顶齿廓曲线。得到的外齿轮齿顶齿廓曲线a1在111上的方程表达式为

同样地,得到内齿轮齿顶齿廓曲线a2的方程表达式为

2.2 齿根齿廓
已知内齿轮齿顶齿廓曲线方程式(11)及传动比=2/1,根据齿轮啮合原理,与内齿轮齿顶齿廓a2共轭的外齿轮齿根齿廓曲线d1可表示为



式(13)存在2个解:
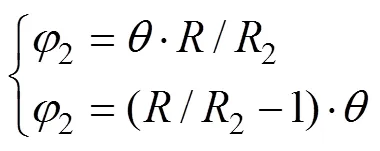
第1个解对应着与内齿轮齿顶齿廓共轭的外齿轮齿顶齿廓,因此,将式(11)和式(14)中第2式代入式(12)得到外齿轮齿根齿廓曲线d1的方程表达式。

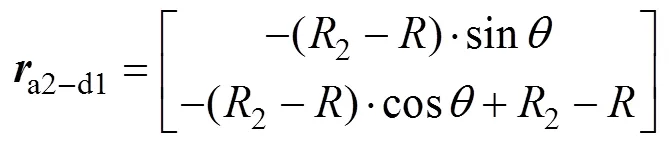
由式(16)可知外齿轮齿根齿廓与内齿轮齿顶齿廓的啮合线为一圆弧(半径为2−),且与设计的圆弧啮合线01在节点0相切。
同样地,内齿轮齿根齿廓曲线d2可表示为
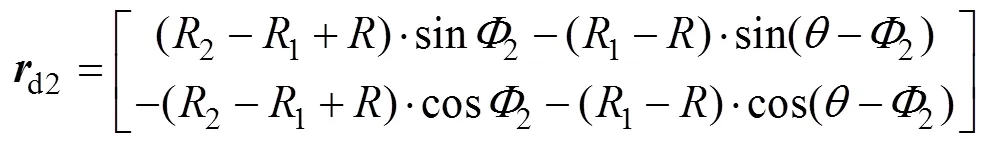
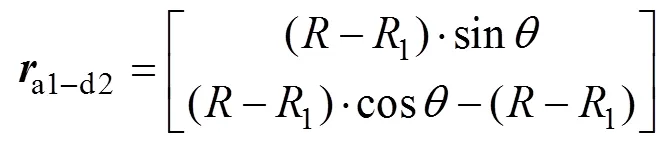
根据式(18)可知内齿轮齿根齿廓与外齿轮齿顶齿廓的啮合线为一圆弧(半径为−1),且与设计的圆弧啮合线01在节点0相切。
2.3 插齿齿条齿廓
已知外齿轮齿廓曲线方程表达式及外齿轮与齿条的运动关系式=11,根据共轭原理,得到的与外齿轮齿顶齿廓共轭的齿条齿根齿廓可表示为

与外齿轮齿根齿廓共轭的齿条齿顶齿廓可表示为

齿条的齿廓由齿顶齿廓和齿根齿廓2部分组成,分别与外齿轮的齿根齿廓和齿顶齿廓共轭,在排除根切的情况下可通过齿条刀具可加工出完整的外齿轮齿廓曲线。
2.4 内齿轮齿根齿廓修形


图3 新型大重合度内啮合齿轮啮合线
2.5 根切和干涉检查
齿轮齿廓曲线在奇异点发生相对滑动,即d/d0时,在奇异点处可能出现根切[1]。对外齿轮、内齿轮及齿条齿廓曲线进行奇异点检查后发现节点0是齿顶齿廓和齿根齿廓的奇异点。然而,由于节点0位于齿顶齿廓和齿根齿廓的端点,且啮合线在节点0的切向量垂直于中心连线12,共轭齿廓在节点0啮合时,其公法线的方向与相同,则在0点处压力角为0°,这种情况与摆线齿在其节点处的情况相同[1]。因此,虽然节点0是齿廓曲线奇异点,但不会产生根切。在齿轮啮合过程中,外齿轮齿顶齿廓与内齿轮齿顶齿廓共轭,外齿轮的齿根齿廓与内齿轮齿顶齿廓共轭,且内齿轮齿根齿廓经修形后不参与啮合,因而不会发生齿顶干涉。但大重合度内啮合齿轮的齿顶齿廓与齿顶齿廓共轭,将发生径向干涉,故只能采用轴向安装的方式完成齿轮装配。


图4 新齿形内啮合齿轮三维模型及接触区仿真结果
3 齿轮啮合特性分析
齿轮啮合特性主要包括重合度、相对滑动率、相对法曲率和齿轮接触疲劳强度、齿根弯曲疲劳强度等指标[13],下面将研究新型大重合度内啮合齿轮啮合特性并与渐开线内啮合齿轮进行对比。
3.1 重合度


表1 新齿形和渐开线齿形内啮合齿轮重合度
3.2 相对滑动率
相对滑动率是衡量齿面磨损和齿轮润滑条件的重要指标,相对滑动率降低,齿面磨损减小,润滑条件越好。设d1和d2分别为外齿轮和内齿轮齿廓曲线的弧长元素,满足ds=|dr/dθ| (=1,2),则共轭齿轮相对滑动率[8]可定义为

新齿形内啮合齿轮相对滑动率曲线如图5(a)所示。新齿形的啮合过程可分为2个阶段:当2>0时,外齿轮齿顶齿廓与内齿轮齿顶齿廓在啮合线01上啮合,接触点沿齿廓曲线从齿顶滑动到节点;当2<0时,外齿轮齿根齿廓与内齿轮齿顶齿廓在啮合线02上啮合,外齿轮接触点沿齿根齿廓从节点滑动到齿根,内齿轮接触点沿齿顶齿廓从节点返回齿顶,因此新齿形的相对滑动率曲线在节点处0(2=0)出现拐点。渐开线齿形相对滑动率曲线如图5(b)所示。对比图5(a)和5(b)可以发现:新齿形的相对滑动率为定值,且相比渐开线齿形的相对滑动率大大降低,有利于齿轮润滑及降低齿面磨损。
(a) 新齿形;(b) 渐开线齿形
1—相对滑动率1;2—相对滑动率2。
图5 相对滑动率曲线
Fig. 5 Curves of sliding ratios of tooth profiles
3.3 相对法曲率
相对法曲率越小,接触区越大。新齿形内啮合齿轮的相对法曲率曲线如图6(a)所示。由于节点0为奇异点,在该点共轭齿廓的相对法曲率为无穷大。当2>0时,新齿形齿顶齿廓与齿顶齿廓为凸−凸接触,而渐开线内啮合齿廓为凹−凸接触,因此与渐开线内啮合齿轮相对法曲率相比,新齿形内啮合齿轮相对法曲率较大,接触区较小;当2<0时,新齿形齿根齿廓与齿顶齿廓凹−凸接触,其相对法曲率降低,接触区增大。鉴于新齿形重合度大,单齿承载载荷低,因此,下面将进一步研究新齿形在齿面接触强度方面相较于渐开线齿形的优劣。

(a) 新齿形;(b) 渐开线齿形
3.4 加载接触分析
利用有限元方法研究了加载条件下齿轮接触区位置和大小、齿面接触强度和齿根弯曲强度等[13−14]。为避免啮合过程中齿顶应力集中,对齿顶进行倒角处理,因此齿轮重合度减小。新齿形内啮合齿轮外齿轮在500 N∙m加载力矩下的应力云图如图7所示。此时共轭齿廓在节点啮合,共有6对轮齿参与啮合,最大齿面接触应力为592.5 MPa,出现在节点附近,最大齿根弯曲应力为198.654 MPa。图8所示为新齿形内啮合齿轮及渐开线内啮合齿轮外齿轮分别在加载力矩为100,300和500 N∙m条件下1个啮合周期内的齿面接触应力曲线和齿根弯曲应力曲线。由图8可知:齿轮的齿面接触应力和齿根弯曲应力随着加载力矩增大而增大。新齿形的最大齿面接触应力及最大齿根弯曲应力比渐开线齿形的低。当新齿形外齿齿根齿廓与内齿齿顶齿廓凹凸接触时,接触区较大,齿面接触应力较低。当外齿齿顶齿廓与内齿齿顶齿廓凸−凸接触时,接触区减小,齿面接触应力增大。与渐开线齿形弯曲应力相比,新齿形齿根弯曲应力明显降低。

图7 新型大重合度内啮合外齿轮应力云图(加载力矩为500 N∙m)
Fig. 7 Stress distribution of pinion to the novel internal gear drive
4 齿轮样件试制
新齿形齿轮的加工精度要求较高,只有合理地选择加工设备和加工工艺才能满足精度要求。新齿形内啮合齿轮可利用插齿齿条加工出外齿轮,利用与外齿轮齿廓相同的插齿刀加工出内齿轮,并通过数控加工完成内齿轮齿根齿廓修形。随着数控加工设备加工能力的提升,特殊齿形齿轮的加工正逐渐变得和普通齿轮的加工一样简单、高效。新齿形齿轮同样可以采用铣齿、插齿及磨齿的工艺进行大批量生产。对于小批量齿轮的加工,可完全采用数控加工,本文作者采用高精度的慢走丝线切割加工出新齿形齿轮样件,使用的机床型号为沙迪克AQ560L,加工精度达到0.005 mm,表面质量接近磨削水平。利用红丹粉检测接触区,结果如图9所示。由图9可知:共有7对轮齿参与啮合,与图4中接触区仿真结果大致一致。
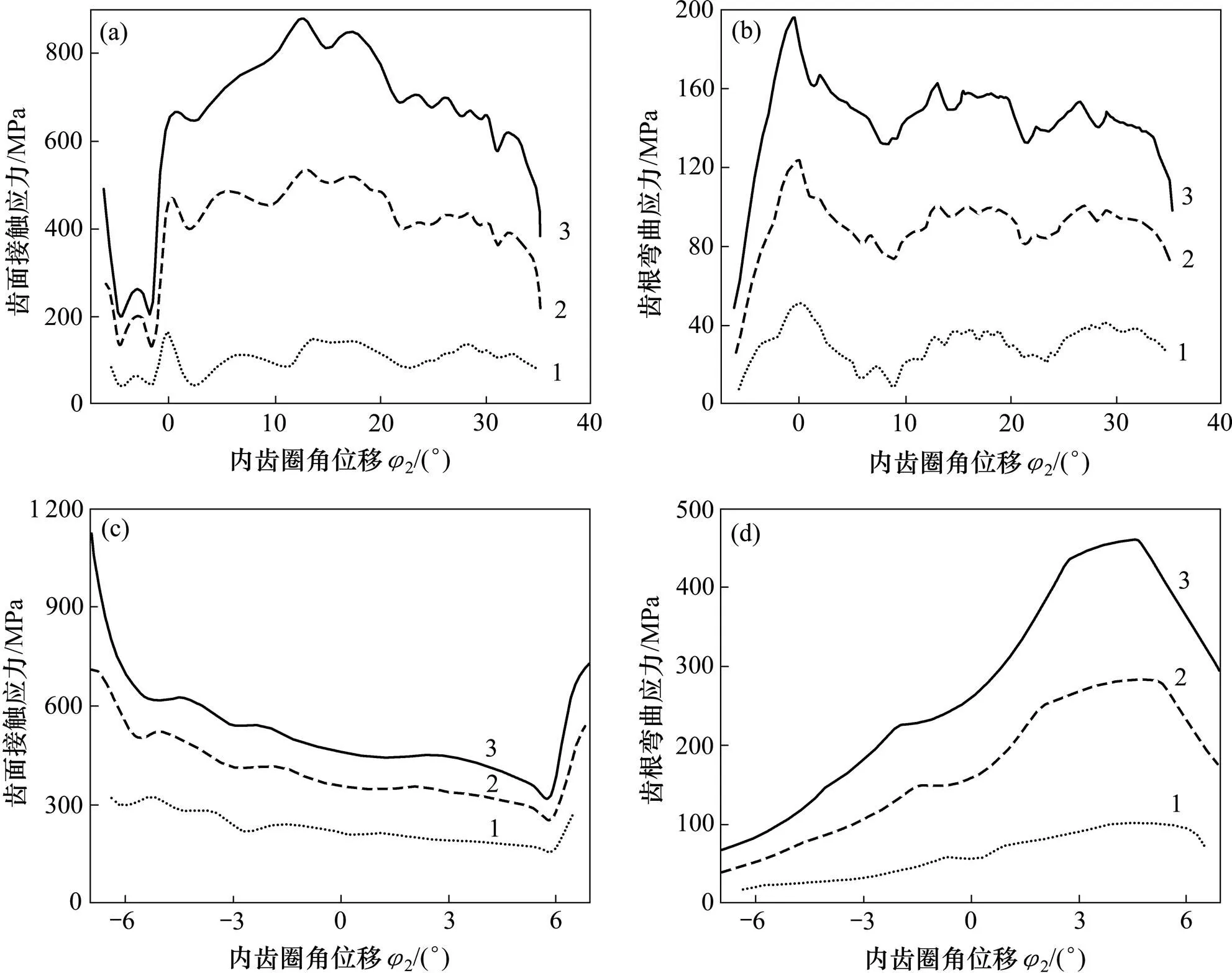
(a) 新齿形齿面接触应力曲线,(b) 新齿形齿根弯曲应力曲线;(c) 渐开线齿形齿面接触应力曲线,(d) 渐开线齿形齿根弯曲应力曲线 加载力矩/(N∙m):1—100;2—300;3—500。

(a) 齿轮样件;(b) 外齿轮接触区域;(c) 内齿轮接触区域
5 结论
1) 新齿形内啮合齿轮的重合度大大提高,对齿数差较小的齿轮对其重合度可达到渐开线齿形的4倍以上。
2)新齿形内啮合齿轮不会发生根切现象,也不会发齿顶干涉现象。
3) 与渐开线内啮合齿轮相比,新齿形相对滑动率大大降低,有利于齿轮润滑及降低齿面磨损,其相对法曲率较大;其齿面接触应力和齿根弯曲应力显著减低,有利于提高承载能力、降低齿面磨损、提升精度保持性、延长使用寿命。
4) 齿数比为38/53的内啮合齿轮有7对轮齿啮合,达到设计要求。
[1] LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. Oxford: Cambridge University Press, 2004: 56.
[2] ROSEN K M, FRINT H K. Design of high contact ratio gears[J]. Journal of the American Helicopter Society, 1982, 27(4): 65−73.
[3] 李发家, 朱如鹏, 鲍和云, 等. 高重合度与低重合度齿轮系统动力学分岔特性对比分析[J]. 中南大学学报(自然科学版), 2015, 46(2): 465−471. LI Fajia, ZHU Rupeng, BAO Heyun, et al. Contrastive analysis of dynamic bifurcation characteristics between high contact ratio and low contact ratio gears system[J]. Journal of Central South University(Science and Technology), 2015, 46(2): 465−471.
[4] 赵富强. 细高齿齿形优化设计及有限元强度分析[D]. 太原:太原理工大学机械工程学院, 2009: 5−7. ZHAO Fuqiang. Optimal design on the tooth profile of high tooth gear and its finite element strength analysis[D]. Taiyuan: Taiyuan University of Technology. College of Mechanical Engineering, 2009: 5−7.
[5] 郭敬滨, 王娴, 刘海军, 等. 摆线齿轮误差的测量及修形量计算[J]. 天津大学学报, 2011, 44(1): 85−89. GUO Jingbin, WANG Xian, LIU Haijun, el at. Measurement of cycloidal gear error and calculation of modification[J]. Journal of Tianjin University, 2011, 44(1): 85−89.
[6] 王三民, 纪名刚. 高速大重合度直齿圆柱齿轮的齿廓最佳修形研究[J]. 航空学报, 1996, 17(1): 121−124. WANG Sanmin, JI Minggang. Study on the best profile modification of high-speed spur gears with high-contact-ratio[J]. Acta Aeronautica et Astronautica Sinica, 1996, 17(1): 121−124.
[7] 牛嗥, 梁桂明. 大重合度圆柱斜齿轮的优化设计[J]. 洛阳工学院学报, 1994, 15(4): 68−71. NIU Hao, LIANG Guiming. Optimal design of high contact ratio bevel gears[J]. Journal of Luoyang Institute of Technology, 1994, 15(4): 68−71.
[8] DONG Huimin, TING K L, YU Bowen, et al. Differential contact path and conjugate properties of planar Gearing transmission[J]. Journal of Mechanical Design, 2012, 134(6): 061010−061020.
[9] 王建, 罗善明, 苏德瑜. 基于压力角的高重合度齿轮主动设计及特性分析[J]. 中南大学学报(自然科学版), 2014, 45(11): 3792−3799. WANG Jian, LUO Shanming, SU Deyu. Active design and characteristics analysis of high contact ratio gears based on pressure angle[J]. Journal of Central South University(Science and Technology), 2014, 45(11): 3792−3799.
[10] 魏伟锋, 张广鹏, 杜真一, 等. 参数化直线共轭内啮合泵齿廓设计方法[J]. 机械工程学报, 2014, 50(3): 49−55. WEI Weifeng, ZHANG Guangpeng. DU Zhenyi, et al. Design method of internal rotary gear pump by parameterized line conjugated tooth profile[J]. Journal of Mechanical Engineering, 2014, 50(3): 49−55.
[11] FONG Zhanghua, CHIANG T W, TSAY C W. Mathematical model for parametric tooth profile of spur gear using line of action[J]. Mathematical and Computer Modeling, 2002, 36(4): 603−614.
[12] 吴序堂. 齿轮啮合原理[M]. 北京: 机械工业出版社, 1982: 16−17. WU Xutang. Theory of gearing[M]. Beijing: China Machine Press, 1982: 16−17.
[13] 郭辉, 赵宁, 方宗德,等. 基于接触有限元的面齿轮传动弯曲强度研究[J]. 航空动力学报, 2008, 23(8): 1438−1442. GUO Hui, ZHAO Ning, FANG Zongde, et al. Research on bending strength of face-gear transmission based on contact finite element method[J]. Journal of Aerospace Power, 2008, 23(8): 1438−1442.
[14] 唐进元, 刘艳平. 直齿面齿轮加载啮合有限元仿真分析[J]. 机械工程学报, 2012, 48(5): 124−131. TANG Jinyuan, LIU Yanping. Loaded meshing simulation of face-gear drive with spur involute pinion based on finite element analysis[J]. Journal of Mechanical Engineering, 2012, 48(5): 124−131.
(编辑 伍锦花)
Design and analysis of internal gear drive with arc contact path
WANG Yanzhong, LI Yuan, REN Shaoying, ZHAO Pengkun
(School of Mechanical Engineering & Automation, Beihang University, Beijing 100191, China)
A high contact ratio internal gear drive with arc contact path was proposed for internal gear transmission. The circular arc connecting the intersection point of addendum circles and the intersection point of pitch circles was chosen as the path of contact. The addendum tooth profiles of pinion and internal gear conjugated with each other were constructed based on the given path of contact. According to gearing theory, the dedendum tooth profile was designed as conjugate curve of the addendum tooth profile of the mating gear and modification of dedendum tooth profile to internal gear was carried out. Geometric properties analysis and loaded contact analysis of the novel internal gear were also carried out. The results show that undercutting and addendum interference do not occur for the novel internal gear. The novel internal gear drive has higher contact ratio, smaller sliding ratio, but bigger induced curvature compared with the involute internal gear drive. The stress, especially the bending stress of the novel high contact ratio internal gear drive decreases remarkably. The novel high contact ratio internal gear with tooth number of 38/53 has 7 tooth being in meshing, which confirms the high contact ratio for the novel internal gear drive.
high contact ratio; internal gear; contact path; loaded tooth contact analysis
10.11817/j.issn.1672-7207.2018.05.013
TH132.417
A
1672−7207(2018)05−1118−08
2017−05−20;
2017−06−27
“十二五”国家科技支撑计划(2014BAF08B01) (Project(2014BAF08B01) supported by the National Science and Technology Pillar Program during the 12th “Five-year” Plan Period of China)
王延忠,博士,教授,博士生导师,从事齿轮传动、摩擦片设计研究;E-mail: yzwang63@126.com
