接触载荷作用下非均质材料表层应力集中分析

杨万友，周青华，王家序，杨勇，苗强



接触载荷作用下非均质材料表层应力集中分析

杨万友，周青华，王家序，杨勇，苗强

(四川大学 空天科学与工程学院，四川 成都，610065)

利用数值化等效夹杂方法分析接触载荷作用下规则分布杂质单元影响材料表层最大von Mises 应力大小和位置，并与相同工况下均质材料分析结果进行对比。在此基础上，研究不同分布参数下正态分布杂质单元对材料应力集中行为的影响。研究结果表明：在特定接触载荷作用下，均质材料表层最大von Mises 应力随摩擦因数增大而增大，但杂质单元的存在将改变最大von Mises 应力位置变化规律。非均质材料基体表层应力集中随分布杂质单元方向平均坐标值增大而逐渐增大；随方向平均坐标值增大而逐渐减小；随杂质单元半径增大而先增后减；分布杂质单元体积分数增大将导致基体最大von Mises应力上升。

接触载荷；非均质材料；应力集中；失效

传递运动和动力的界面往往直接决定航空、航天及机械等领域重要装备关键零部件传动性能，其中材料表层质量是影响零部件界面性能的关键因素。然而，工程材料中不可避免地存在如杂质、裂纹等缺陷[1−2]。在接触载荷作用下，这些缺陷的存在将引起材料表层甚至表面应力集中，诱发零部件破坏失效[3−4]。前期针对材料接触应力行为的研究建立在所分析材料为均质材料的理想条件之上[5]，然而材料中分布的不同程度缺陷容易导致局部应力集中[3]。针对该类问题，国内外研究者利用有限元等数值模拟方法开展了大量研究。CHOI等[6]利用考虑晶体滑移和形变孪晶的晶体塑性有限元法来模拟面内压缩过程中AZ31镁合金的空间应力集中表现，其结果表明形变孪晶在非孪晶晶粒与孪晶晶粒的晶界之间会加剧局部应力集中。冯磊 等[3]利用有限元法分析非均质材料受单调拉伸和循环拉压载荷条件下夹杂物周围的局部力学行为，研究夹杂性能、位置、多夹杂、循环塑性对局部应力集中的影响。KUBAIR等[7]用数值化方法研究了材料的非均匀特性对由功能梯度材料板上圆孔产生的应力集中因子的影响，其结果表明当材料杨氏模量从圆孔处向外逐渐增大时，应力集中因子减小。CERIT等[8−10]也开展了类似研究。有限元等方法在研究非均质材料应力集中问题时，由于材料内部微结构的复杂性，往往建模困难；且随着分析网格数目的增加，有限元等方法的时间和内存消耗急剧增大，导致无法进行精确求 解[11]。部分研究者尝试用解析方法来替代数值模拟方法进行该类问题研究。YU等[12]通过改进等效夹杂方法，对在外载作用下2个理想固结在一起的半无限体中嵌入椭球形杂质的弹性场进行了求解。除等效夹杂方法外，MUSKHELISHVILI[13]提出复变方法来处理二维杂质问题的求解。该方法已被很多研究者采 用[14−15]。然而，上述针对非均质材料应力场求解的解析方法只能处理简单形状微观单元问题。本文作者基于前期研究提出用于求解非均质材料弹性场的半解析方法[16]，对在线接触载荷作用下非均质材料表层应力集中问题进行研究。

1 非均质材料应力集中分析

1.1 均质材料应力集中分析

图1所示为在线接触载荷作用下的均质材料接触模型及其特性(其中vm,max为最大von Mises应力)。首先利用接触模型(见图1(a))对均质材料应力集中行为进行研究。半径为的载荷作用于弹性模量m为 210 GPa，泊松比m为0.3的半无限均质材料基体上，基体表面与轴平行。半圆形载荷在直角坐标系下沿轴对称分布，最大正向载荷为，最大切向载荷可通过摩擦因数求得，即=。利用SMITH等[17]提出的算法，将摩擦因数由0变化至1，计算可得下表面最大应力和位置变化，如图1(b)所示。

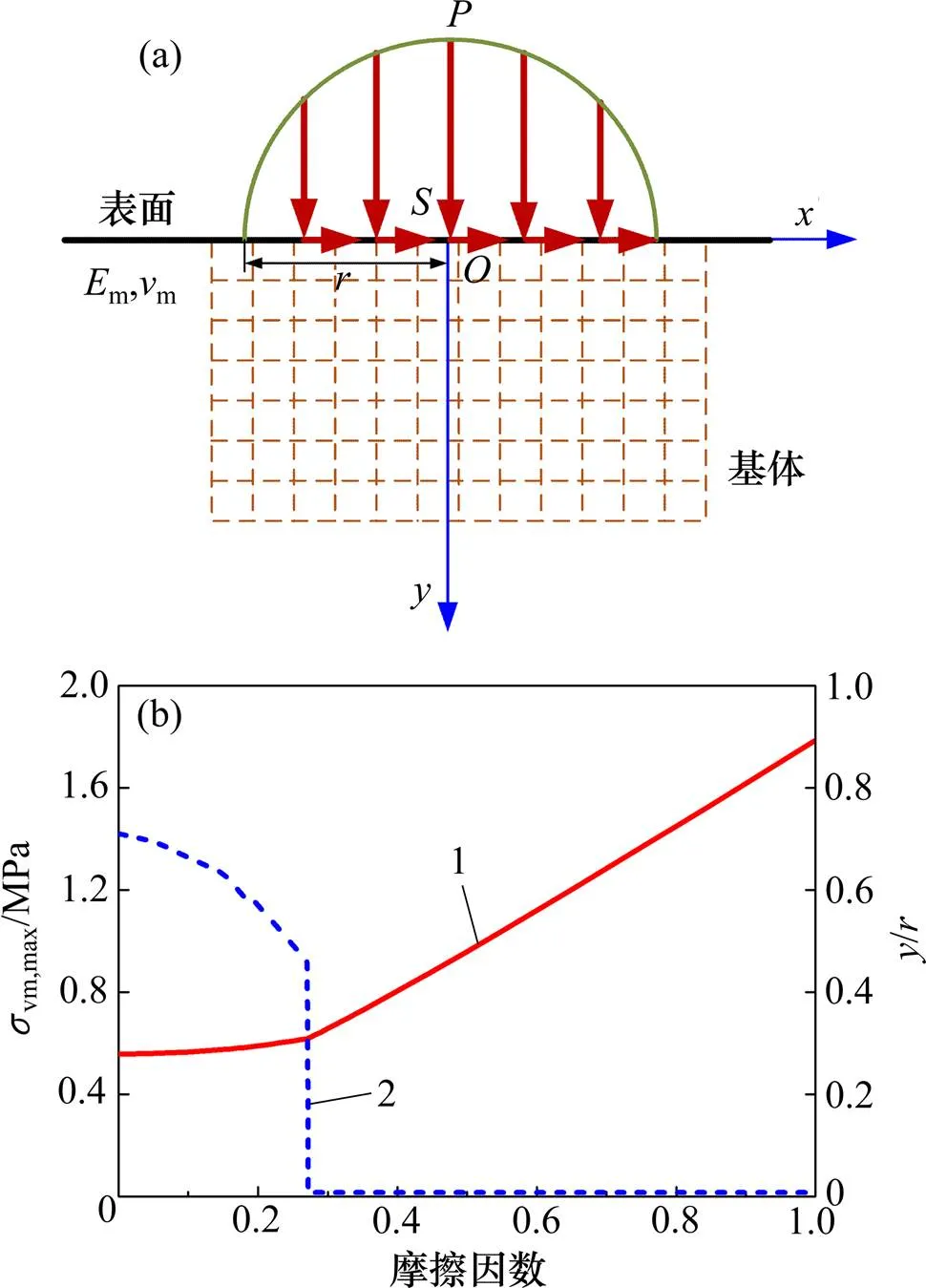
(a) 均质材料线接触模型；(b) 不同摩擦因数下基体最大von Mises应力及其位置

从图1(b)可以看出：当摩擦因数为0~0.273时，均质材料下表面最大von Mises应力增长较为缓慢，但当摩擦因数大于0.273之后却呈线性增长。当小于0.273时，最大von Mises应力位置保持在下表面，但逐步向材料表面靠近；然而当=0.273时，最大应力位置发生突变，从下表面直接上移到表面。最大von Mises应力位置往往也称为材料的第一屈服点[18]，对于材料疲劳失效行为起着决定性作用。故当大于0.273时，线载荷作用下均质材料的最大von Mises应力将在表面产生，极易导致表面磨损与剥落，造成接触零部件的破坏失效。

1.2 非均质材料应力集中分析

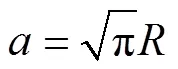
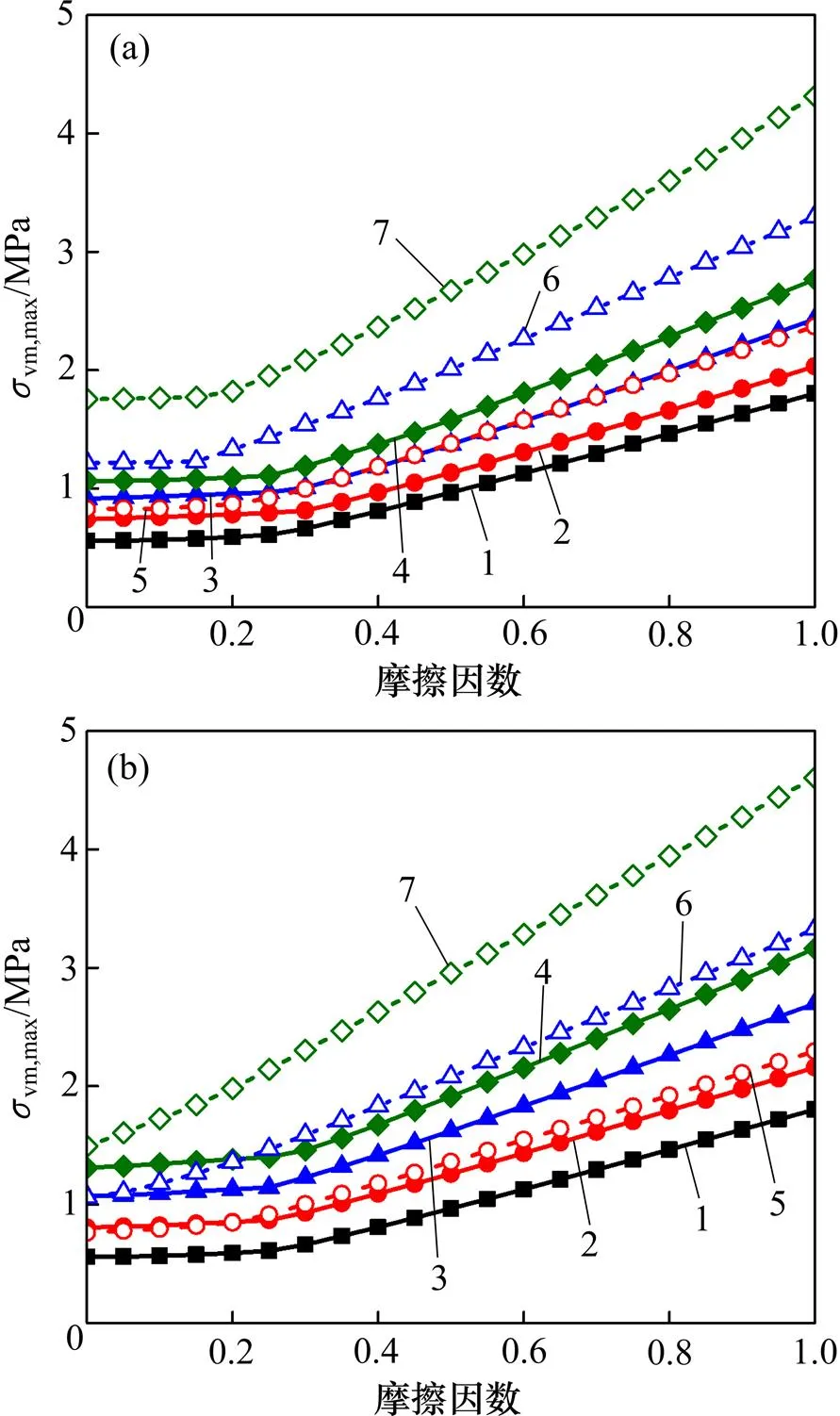
从图2(c)~(d)可以看出：与均质基体情形类似，当含规律分布杂质单元时，基体最大von Mises 应力同样随摩擦因数增大而先缓慢增大，之后逐渐呈近似线性增长。但由于杂质单元的加入，在相同摩擦因数作用下，基体下表面最大von Mises应力都比均质材料的要大，且软杂质单元较硬杂质单元增大更显著。由于规律分布杂质单元的存在，最大von Mises 应力位置随着摩擦因数增大，从下表面逐渐分段阶跃上移至接近表面位置(该位置由杂质阵列中表层单元位置决定)。2种圆形杂质引起的最大应力位置阶跃上移最明显的阶段分别发生在=0.31和=0.24处；2种正方形杂质引起的最大应力位置阶跃上移最明显的阶段分别发生在=0.27和=0.22处。由图2(c)与图1(b)对比可知：圆形硬质单元可相对延缓材料第一屈服点跳跃至近表面位置，而软杂质的存在则使得当摩擦因数较小时材料第一屈服点就已上移到近表面，增大材料发生破坏的风险。由图2(d)与图1(b)对比可知：基体中不管是存在正方形硬质单元还是软质单元，都使得摩擦因数较小时材料第一屈服点就已上移到近表面，加剧材料破坏的发生。

当摩擦因数=0.4时，均质材料和含规则分布杂质单元的非均质基体应力场如图3所示(其中vm为von Mises应力)。从图3(a)可以看出：均质材料在摩擦力作用下，主要应力分布集中于表面。而在含规则分布异质单元的非均质材料内部应力则被极大地扰动，并且在杂质单元附近易产生应力集中。从图3(b)~(e)可看出：硬、软2种杂质都会导致基体产生应力集中，且软杂质更为显著。圆形硬质单元周围的应力集中程度要明显比正方形硬质单元的低，而圆形与正方形软质单元的应力集中程度则相当。图3所示结果有效地解释了图2中的模型计算结果。

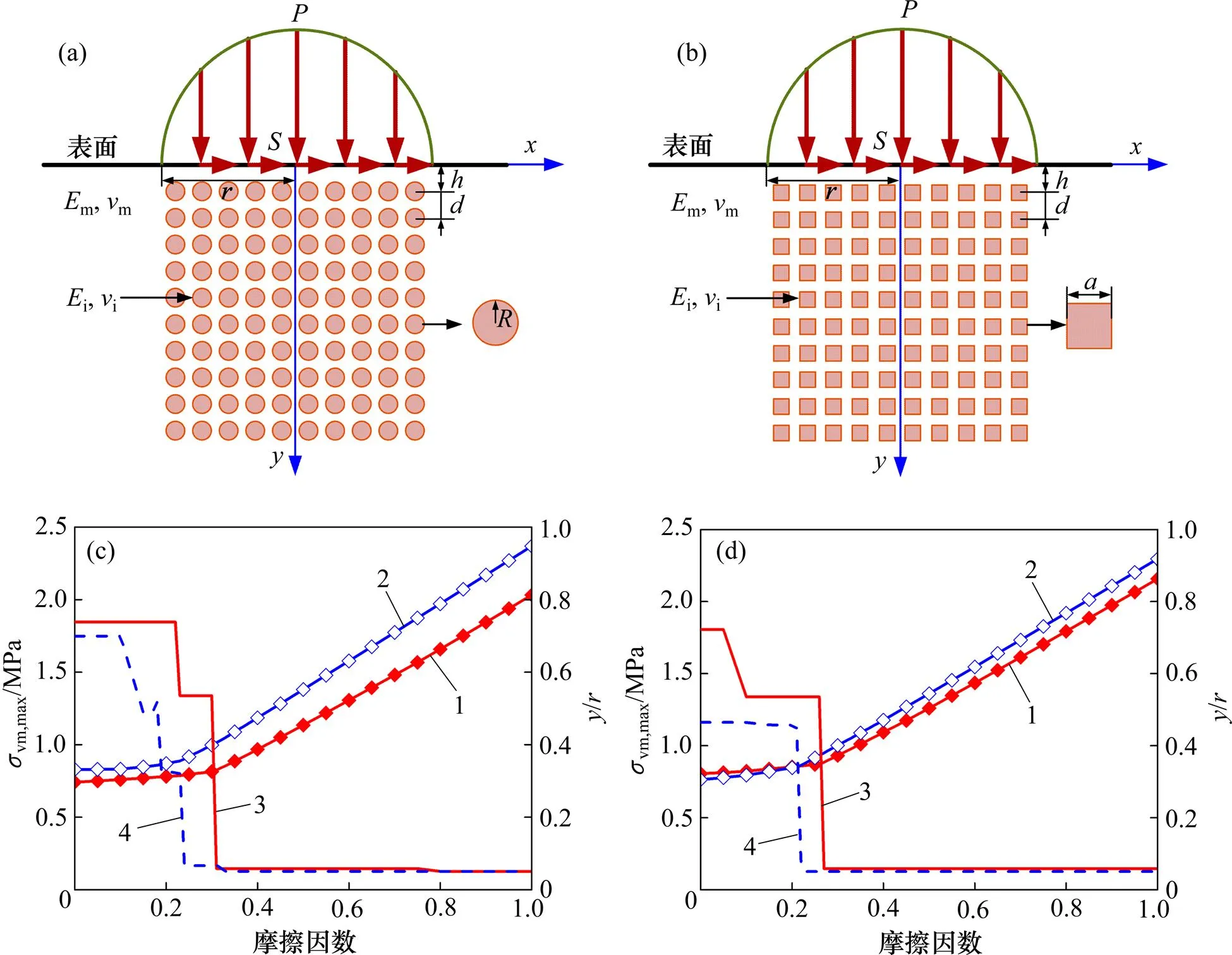
(a) 圆形规则分布杂质接触模型：(b) 正方形规则分布杂质接触模型；(c) 不同摩擦因数下含有规则分布圆形杂质基体最大von Mises应力及其位置；(d) 不同摩擦因数下含有规则分布正方形杂质基体最大von Mises应力及其位置

进一步利用规则分布杂质接触模型(见图2(a)~ (b))研究单元材料属性变化对基体应力集中行为的影响。分别设定杂质单元与基体弹性模量比=i/m(或=m/i)为1，2，4和8，这2种材料泊松比相同，即m=i=0.3。经计算分析得到在不同摩擦因数作用下，因分布杂质弹性模量对基体最大von Mises应力影响如图4所示。由图4可知：在相同特定载荷作用下含有规则分布杂质单元的非均质材料中产生的最大von Mises 应力比均质材料的高。异质单元与基体材料属性差异越大，导致下表面应力集中更为严重。杂质形状的不同，导致下表面应力场扰动相异，使得最大von Mises应力随摩擦因数的变化幅度有所差别。

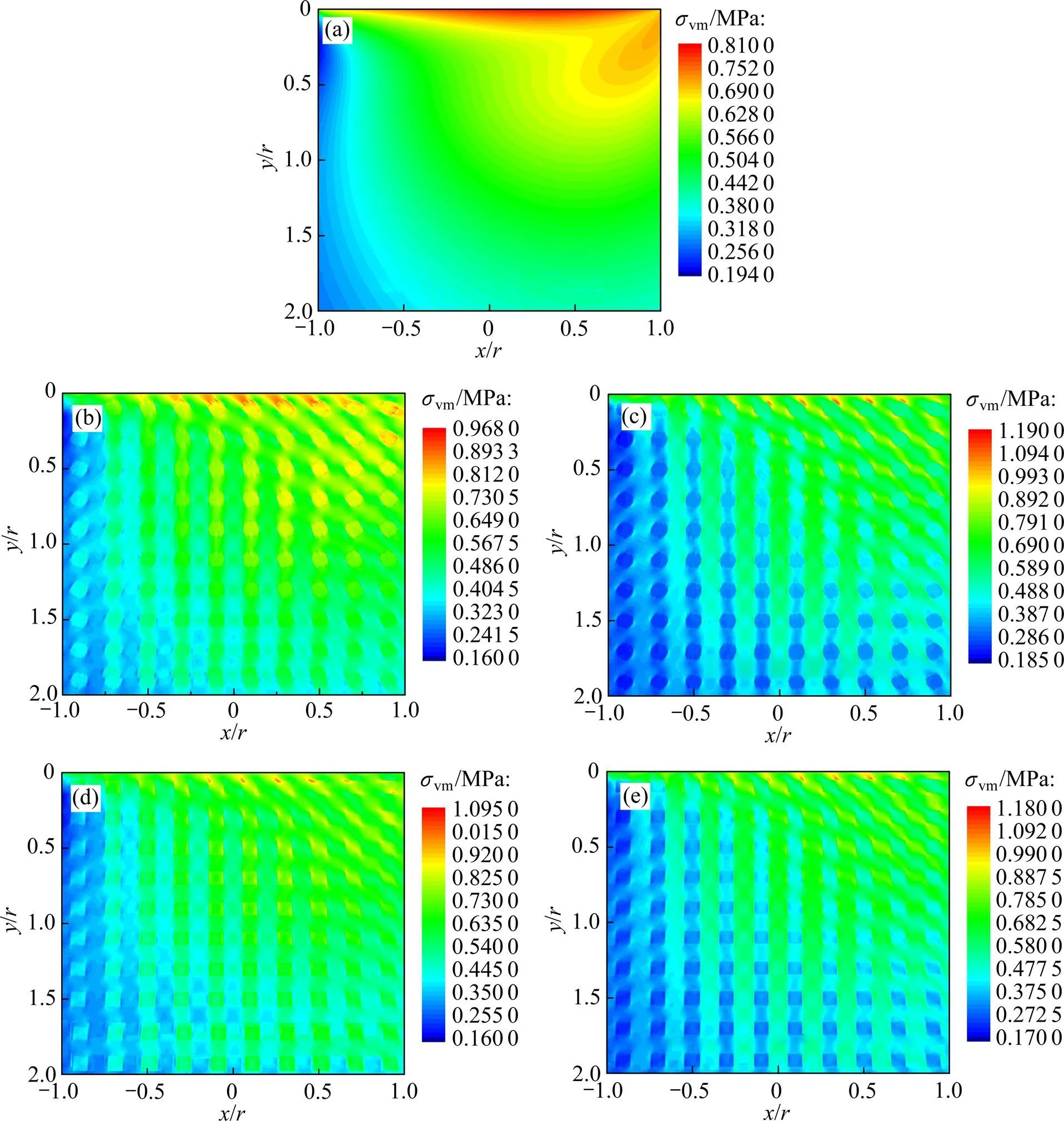
(a) 均质材料von Mises 应力场；(b) 规则分布圆形硬杂质von Mises应力场；(c) 规则分布圆形软杂质von Mises应力场；(d) 规则分布正方形硬杂质von Mises应力场；(e) 规则分布正方形软杂质von Mises应力场

(a) 规则分布圆形杂质；(b) 规则分布正方形杂质

2 正态分布杂质应力集中参数化研究

材料中杂质、裂纹等缺陷往往呈随机分布，因此，有必要对随机分布杂质单元影响材料应力集中行为进行研究，以期分析结果更贴近工程实际。基于上述分析结果，设定摩擦因数=0.1，以保证材料内部最大应力位于表面之下。在此基础上，对接触载荷作用下含正态分布杂质单元的非均质材料应力响应进行参数化分析。

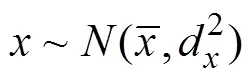
(a) 正态分布杂质接触模型；(b) 正态分布硬杂质von Mises应力场；(c) 正态分布软杂质von Mises应力场

2.1 正态分布杂质x方向平均坐标

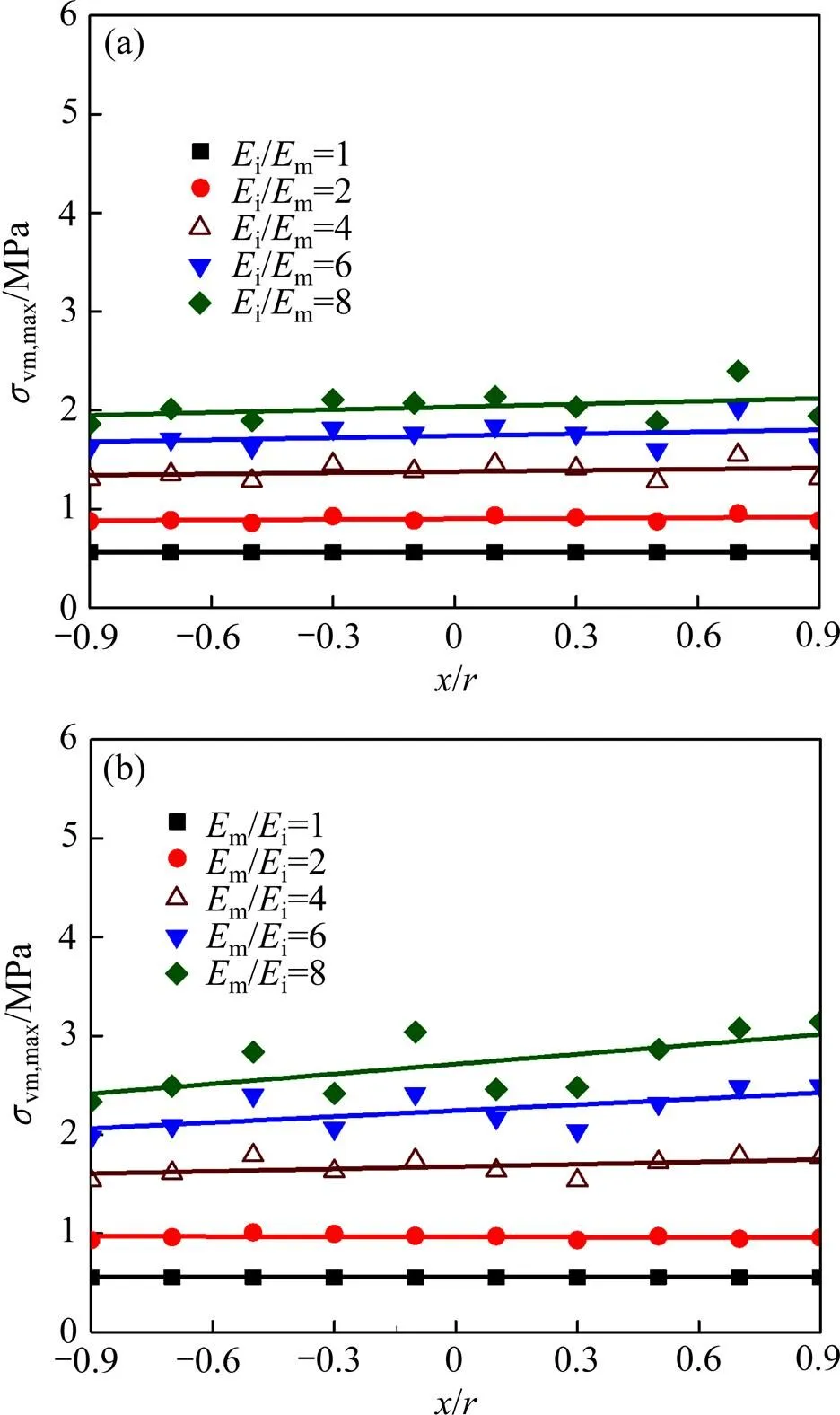
(a) 不同弹性模量硬圆形杂质；(b) 不同弹性模量软圆形杂质

2.2 正态分布杂质y方向平均坐标

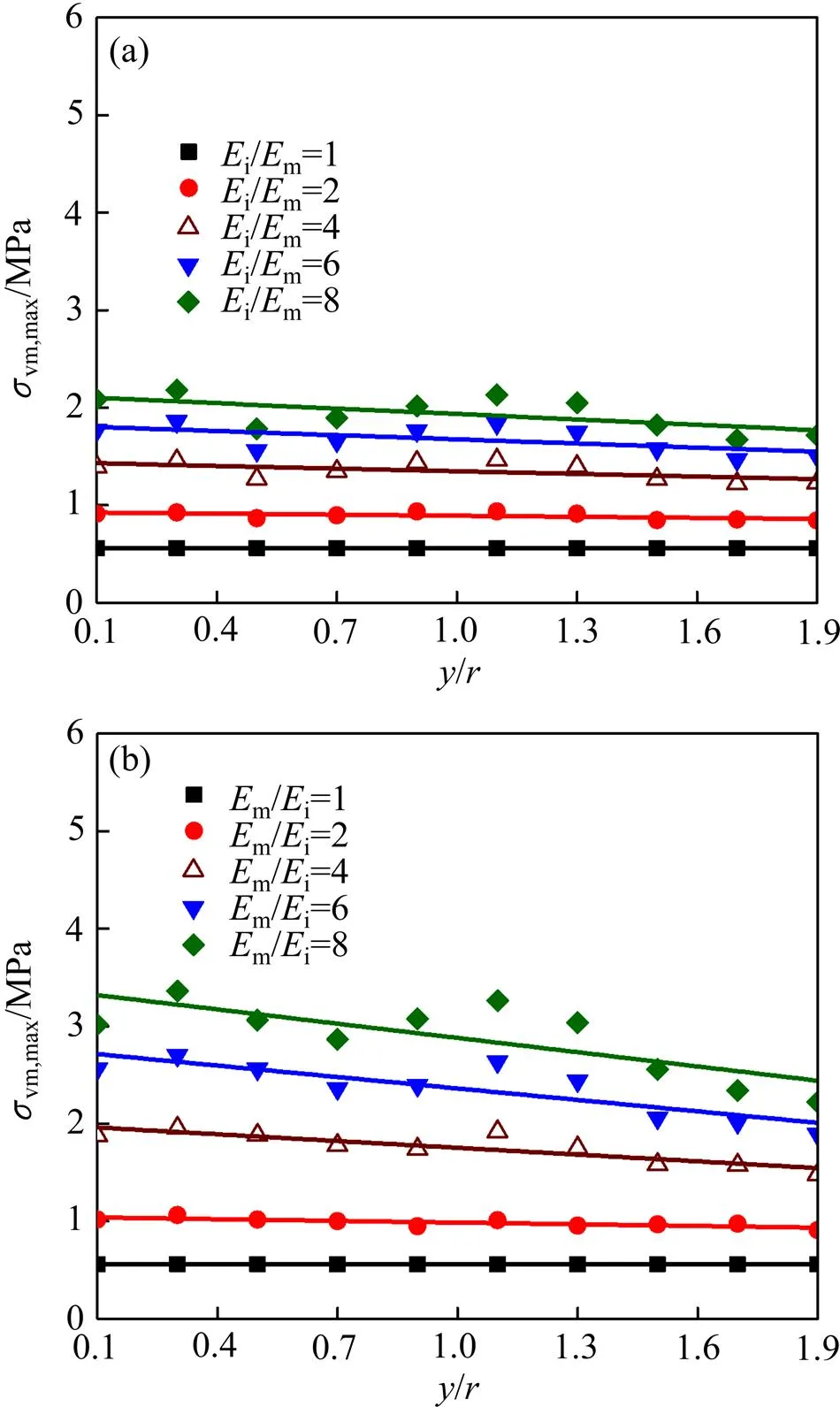
(a)不同弹性模量硬圆形杂质；(b) 不同弹性模量软圆形杂质

2.3 正态分布杂质单元半径

2.4 正态分布杂质单元体积分数

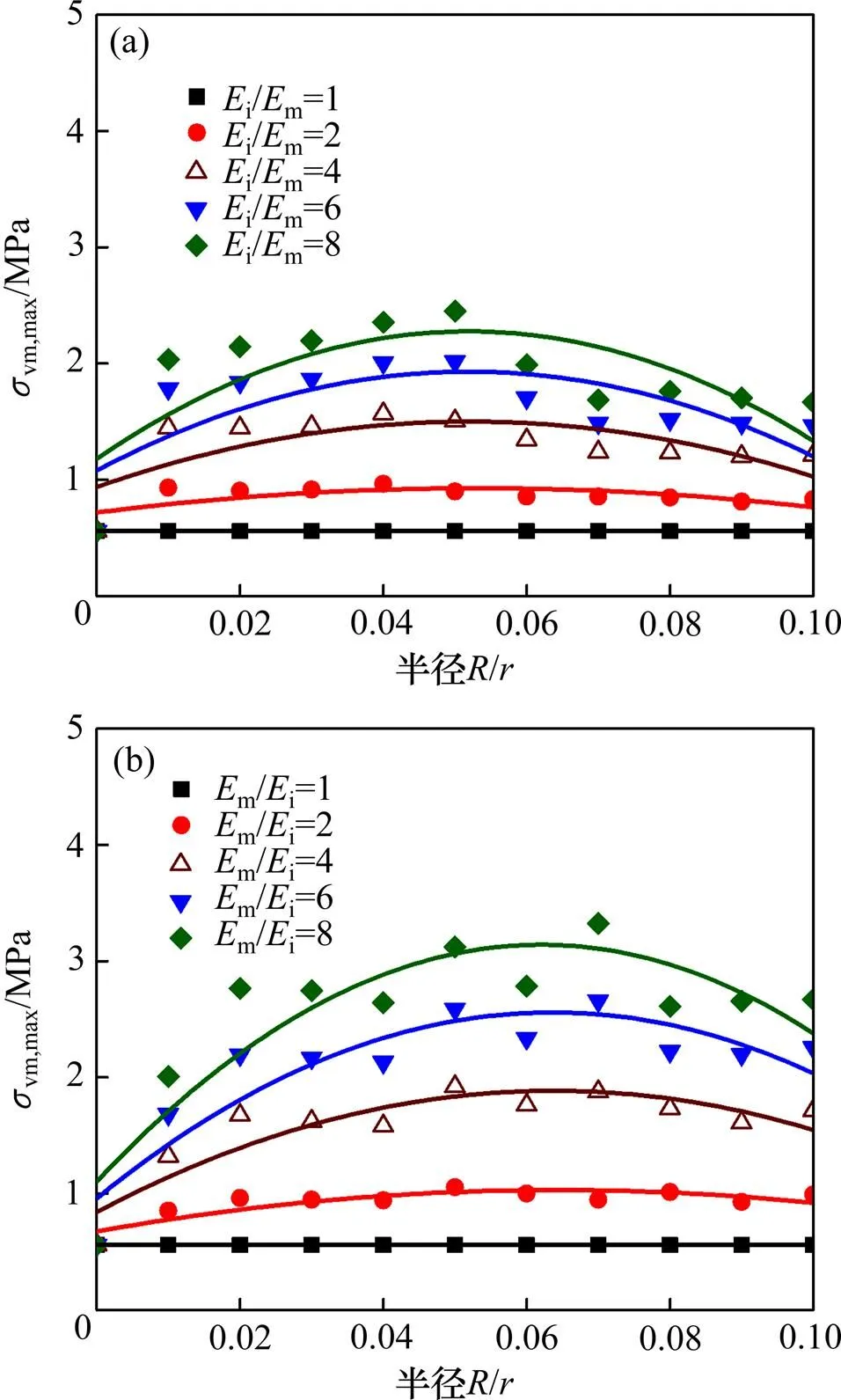
(a) 不同弹性模量硬圆形杂质；(b) 不同弹性模量软圆形杂质

3 结论

1) 在接触载荷作用下，当均质材料的摩擦因数超过一定值时，表面下最大von Mises 应力位置将跳跃到基体表面，从而使得表面磨损加剧。而下表面存在分布杂质单元则会显著影响非均质材料中最大应力位置的分布规律，即最大应力位置随着摩擦因数增大，从下表面逐渐分段阶跃至近表面杂质阵列最表层单元位置。

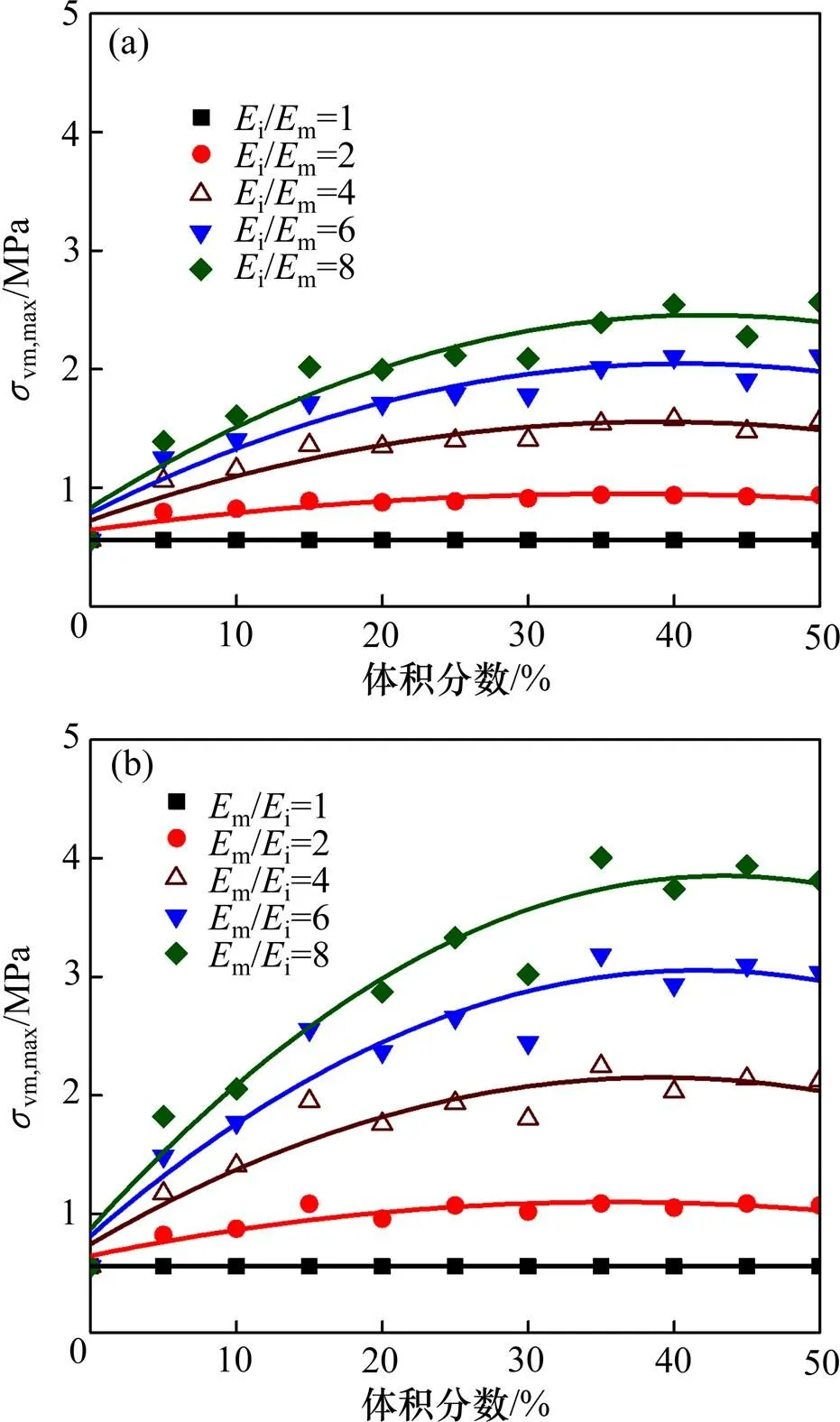
(a) 不同弹性模量硬圆形杂质；(b) 不同弹性模量软圆形杂质

2) 不同形状均布杂质单元对基体下表面应力扰动程度由杂质单元形状及材料的硬质或软质决定。当杂质单元为软质材料时，材料形状对基体下表面应力扰动影响区别并不明显。

3) 正态分布杂质单元与基体材料属性差异越大，更易引起材料内部应力集中，且相应的软质单元引起的基体应力增大较硬质单元的更为显著。

4) 基体最大von Mises 应力将随圆形分布颗粒方向平均坐标的增大而增大，随坐标增大而减小；杂质单元半径增大将引起基体最大应力先增后减；而体积分数增加将加剧材料下表面应力集中。

[1] 王雪明, 谢富原, 李敏, 等. 热压罐成型加筋板L形筋条纤维密实影响因素研究[J]. 航空材料学报, 2011, 31(4): 64−68.WANG Xueming, XIE Fuyuan, LI Min, et al. Experimental research on fiber compaction of L-shaped stiffeners in stiffened skins by autoclave process[J]. Journal of Aeronautica Materials, 2011, 31(4): 64−68.

[2] 顾轶卓, 张佐光, 李敏, 等. 复合材料变厚层板热压成型缺陷类型与成因实验研究[J]. 复合材料学报, 2008, 25(2): 41−46.GU Yizhuo, ZHANG Zuoguang, LI Min, et al. Experimental study on type and cause of defects in variable thickness composite laminates during hot pressing process[J]. Acta Materiae Compositae Sinica, 2008, 25(2): 41−46.

[3] 冯磊, 轩福贞. 非金属夹杂物对材料内局部应力集中的影响[J]. 机械工程学报, 2013, 49(8): 41−48. FENG Lei, XUAN Fuzhen. Effect of non-metallic inclusions on the local stress concentration within materials[J]. Journal of Mechanical Engineering, 2013, 49(8):41−48.

[4] 陈康华, 方玲, 李侠, 等. 颗粒失效对SiCp/Al复合材料强度的影响[J]. 中南大学学报(自然科学版), 2008, 39(3): 493−499. CHEN Kanghua, FANG Ling, LI Xia, et al. Influence of particle failure on strength of SiCp/Al composites[J]. Journal of Central South University(Science and Technology), 2008, 39(3): 493−499.

[5] SADEGHI F, JALALAHMADI B, SLACK T S, et al. A review of rolling contact fatigue[J]. Journal of Tribology, 2009, 131(4): 220.

[6] CHOI S H, KIM D H, PARK S S, et al. Simulation of stress concentration in Mg alloys using the crystal plasticity finite element method[J]. Acta Materialia, 2010, 58(1): 320−329.

[7] KUBAIR D V, BHANU-CHANDAR B. Stress concentration factor due to a circular hole in functionally graded panels under uniaxial tension[J]. International Journal of Mechanical Sciences, 2008, 50(4): 732−742.

[8] CERIT M, GENEL K, EKSI S. Numerical investigation on stress concentration of corrosion pit[J]. Engineering Failure Analysis, 2009, 16(7): 2467−2472.

[9] ACHOUR T, BOUIADJRA B B, SERIER B. Numerical analysis of the performances of the bonded composite patch for reducing stress concentration and repairing cracks at notch[J]. Computational Materials Science, 2003, 28(1): 41−48.

[10] 徐慧, 伍晓赞, 程仕平, 等. 复合裂纹的应力强度因子有限元分析[J]. 中南大学学报(自然科学版), 2007, 38(1): 79−83. XU Hui, WU Xiaozan, CHENG Shiping, et al. Finite element analysis of stress intensity factor in composite mode crack[J]. Journal of Central South University(Science and Technology), 2007, 38(1): 79−83.

[11] ZHOU Qinghua, JIN Xiaoqing, WANG Zhanjiang, et al. Numerical modeling of distributed inhomogeneities and their effect on rolling contact fatigue life[J]. Journal of Tribology, 2012, 137(1): 313−315.

[12] YU Jiahuan, KUANG Zhenbang. The stress analysis of an ellipsoidal inhomogeneity in dissimilar media[J]. Composites Science and Technology, 2003, 63(7): 955−966.

[13] MUSKHELISHVILI N I. Some basic problems of the mathematical theory of elasticity[J]. The Mathematical Gazette, 1953, 48(365): 351.

[14] KUSHCH V I, SHMEGERA S V, BURYACHENKO V A. Interacting elliptic inclusions by the method of complex potentials[J]. International Journal of Solids and Structures, 2005, 42(20): 5491−5512.

[15] BURYACHENKO V, KUSHCH V. Effective transverse elastic moduli of composites at non-dilute concentration of a random field of aligned fibers[J]. Journal of Applied Mathematics and Physics, 2006, 57(3): 491−505.

[16] 杨万友, 周青华, 王家序, 等. 考虑异质材料的线接触性能建模与分析[J]. 复合材料学报, 2016, 33(8): 1848−1858. YANG Wanyou, ZHOU Qinghua, WANG Jiaxu, et al. Modeling and analysis on line contact performance considering heterogeneous properties of material[J]. Acta Materiae Compositae Sinica, 2016, 33(8): 1848−1858.

[17] SMITH J O, LIU C K. Stresses due to tangential and normal loads on an elastic solid with application to some contact stress problems[J]. Journal of Applied Mechanics-Transactions of the ASME, 1953, 20(2): 157−166.

[18] LI Xiaoyong, WANG Shilong, WANG Zhanjiang, et al. Location of the first yield point and wear mechanism in torsional fretting[J]. Tribology International, 2013, 66(7): 265−273.

(编辑 伍锦花)

Subsurface stress concentration of heterogeneous material under contact loading

YANG Wanyou, ZHOU Qinghua, WANG Jiaxu, YANG Yong, MIAO Qiang

(School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, China)

A numerical equivalent inclusion method was used to analyze the maximum subsurface von Mises stress and its location for heterogeneous materials with regularly distributed heterogeneity elements under contact loading. The obtained results were compared with that of a homogeneous material under the same load. Further, parametric analyses were conducted to investigate the stress concentration caused by normally distributed heterogeneities in heterogeneous materials. The results show that the maximum subsurface von Mises stress of homogeneous material under a given load increases when friction coefficient becomes larger. Location of the maximum von Mises stress changes due to the existence of distributed heterogeneity elements. Subsurface stress concentration of the matrix becomes severer if the averagecoordinate value of the normally distributed heterogeneities increases, or the averagecoordinate value decreases. The maximum von Mises stress of materials rises firstly and then declines as the radius of inhomogeneity increases. The increase of volume fraction in heterogeneity results in a severer stress concentration in the matrix.

contact loading; heterogeneous material; stress concentration; failure

10.11817/j.issn.1672-7207.2018.05.010

TB330

A

1672−7207(2018)05−1095−08

2017−05−20；

2017−06−30

国家自然科学基金资助项目(51435001，51405316)；中央高校基本科研业务费资助项目(2017SCU12021)；航空科学基金资助项目(20150219001) (Projects(51435001, 51405316) supported by the National Natural Science Foundation of China; Project (2017SCU12021) supported by the Fundamental Research Funds for the Central Universities of China; Project(20150219001) supported by Aeronautical Science Foundation of China)

周青华，博士，副教授，从事空间摩擦学与可靠性工程、多尺度优化设计理论研究；E-mail: qh.zhou@foxmail.com