例谈小学数学“板书结构化”的统整效应

江苏海门市证大小学 张玉华

美国著名教育家布鲁纳认为：学习一门学科，就是要掌握这门学科的基本结构。就小学数学而言，知识有的相对独立，但更多的是相互之间可以联系与转换。教师要有分析教材知识结构与编排体系的意识，具备瞻前顾后统领教材的能力。教学时，如果我们能通过板书建立起数学知识的立体网络结构，就能有效地帮助学生在学习的过程中边学边 “串”，最终学生获得的不仅是数学的知识链，更多的是数学思维素养的提升。

一、“板书结构化”具有“连点成线”的统整

心理学中知觉的整体性，是指人们在过去经验的基础上把由多种属性构成的事物知觉串联为一个统一的整体的特性。结构的关联能使知识教学和能力发展呈现一条清晰的脉络，教师应引领学生探索和发现知识点之间相似的呈现过程，并将这一过程进行合理统整。如《认识小数》一课的板书，首先

激活学生过去的认知经验：数位顺序表依次往左伸展，10个一是一个十，10个十是一个百，10个百是一个千……再自然引申出对小数的认识：整数部分往右延伸便产生了小数的需要，把1平均分成10份，一份就是0.1，10个0.1是1，把0.1平均分成10份，一份就是0.01，10个0.01是0.1……学数学就是学关系，“连点成线”的板书，将整数部分和小数部分之间的一个个关系串联，形成完整的线性知识结构体系。

又如《小数的意义》一课，教者用一定意义的线条、箭头、图形等组成了图文并茂的板书，它的特点是形象直观地展示教学内容，以结构渗透思维素养。值得一提的是十分之一和百分之一关系的设计，一个大正方体平均分成10份，每份是十分之一，也就是0.1，如果把这个一份（0.1）再继续分下去，便产生了0.01，这个板书分散了难点，一节课上出了一个体系的跨度。从课堂效果来看，学生学得扎实，一经图示，便一目了然。这种着眼整体、着重联系、着力思维的板书方式妙不可言。

二、“板书结构化”具有“由线铺面”的统整

德国数学家希尔伯特强调：数学科学是一个不可分割的有机整体，它的生命力正是在于各个部分之间的联系。

《认识方程》是小学阶段学习方程的起始课，教学内容大多安排在五年级。对方程的认识，教材上有这样一句话“含有未知数的等式是方程”，我们平时教学也经常围绕这句话展开。张奠宙教授认为：方程的本质是为了求未知数而在已知数和未知数之间建立一种等式关系，这种关系建立后，未知可以和已知一样参与运算、享有同样的地位。可见，学习方程的价值是深入到方程的思想。一位教师在教学《认识方程》时板书如下图，看似简单，

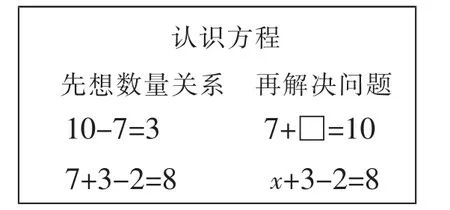
却借“认识方程”这条线展开对方程思想的一系列研究。课始，教者创设了一道情境题：“草地上有7人在踢足球，再来几人，就有10人？”学生在简单的情境中畅所欲言，从开始10－7=3的算术思想抽象为7＋□=10的方程思想。接着，教者又出示了一道改编题：“草地上有人在踢足球，先来了3人，又走了2人，现在草地上有8人，原来有几人？”少数学生先口算后列式：7＋3－2=8，其实从事情发展本身来看，（）+3－2=8更好理解， 于是就有了方程的需要：x＋3－2=8。板书寥寥几笔就呈现了学生的思维，方程教学回溯到了最初始的一年级数学的问题解决中，学生在回望、反思、比较、描述、建构中发展了整体性、逻辑性的认知结构。在螺旋上升的知识系统中，学生理解了方程的意义及为什么需要方程。这份看似简单的板书，却体现了数学思想的结构，不失为一种积极的教学方法。

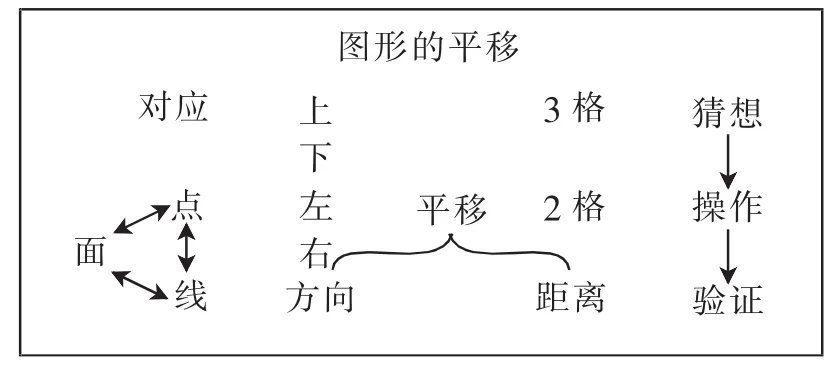
同样，在《图形的平移》的教学中，板书设计也体现了“由线铺面”的结构性。如图，板书从点的平移展开研究，继而研究线段的平移，最终解决面的平移，这是一个由简单到复杂的研究过程。然而教者并没有满足于此，在变式练习中，将面（房子图）逐一分解成其中的一部分三角形，再提取三角形中的线段，最后找出对应的点，学生从感知整体面的平移到局部面的平移，再到线段的平移，最终回归到点的平移，凸显了课程内容的平面结构化。这份板书还提炼了数学学习的基本方法：猜想—操作—验证，促使学生的线性思维逐步向整体的、结构关系的思维迈进。

三、“板书结构化”具有“层层深入”的统整

数学家华罗庚在《数论导引》中，首先强调的是数学的整体性与各部分之间的联系。对“关系”的把握，可以看成是数学学习最重要的任务之一，如果教学时我们能从“关系”出发，将学习置于体系构建中层层深入，学生获得的就不是局部的、零散的知识，而是系统化的、结构化的关系。

如“时、秒、分”这三个时间量本属于一个不可分割的整体，相互联系、彼此依存。教材安排了两课时的教学，为了保持它们之间的联系，有位教师把时分秒整合在一课时教学，板书在这里起到了关键性作用。这份板书对教材进行了重构，层层深入地推动了学生递进式的学习，它重点落在学生对相邻时间单位进率的理解和1时、1分、1秒的体验上，学生从钟面上知道了1大格和1小格表示什么；在体验与探究中，得出了秒针走1小格是1秒；秒钟走1圈，分针走1小格是1分；分针走1圈，时针走了1大格是1时；时针、分针、秒针是同时转动的，它们之间的进率为60。时、分、秒的教学统整在一节课内，离不开“板书结构化”，它把原本抽象、零散的概念，向整体层层推进，凸显了知识的系统化，体现了化散为整的教学思想，培育了学生的结构化思维。

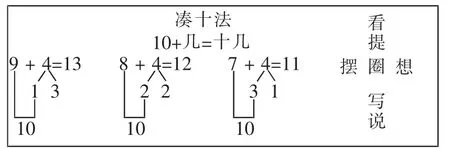
又如：《9加几》是学习20以内进位加法的开始，是在学生学习了20以内的不进位加法和不退位减法的基础上进行教学的。本节课原本是让学生切身探索9＋几的计算，在理解、掌握凑十法算理和算法的同时，明白为什么转化，转化成什么，怎样转化，初步感知转化的思想。从这份板书来看，教者对教材内容进行了大胆整合，将两课时的内容放在一课时内完成，尤其板书中蕴含的探索性学习方法：看—提—（摆—圈—想）—写—说，对计算8＋4和7＋4有很好的迁移和巩固作用，这样的板书引领着学生在比较中学习，认知水平得以层层深化。

四、“板书结构化”具有“整体推进”的统整

数学是一门结构性很强的学科，数学知识不是孤立存在的，而是有着千丝万缕的联系，是整体系统的有机组成。

比如：图形面积的学习跨度大，三年级时学生学习了长方形和正方形的面积，到了五年级才学习平行四边形、三角形、梯形的面积，尽管它们之间的关联性很强，但分散学习使得学生对多边形面积的感知容易碎片化，复习的首要任务就是将零散的知识及时再现并组织架构，使之相融相通。图形面积的复习，是学生已经掌握了长方形、正方形、平行四边形、三角形、梯形面积计算后的一节复习课。通过复习，进一步掌握平行四边形、三角形、梯形等图形的面积计算公式。同时，通过梳理、通融、整合，对多边形面积的计算进行重构，进一步发展结构化思维，提升数学应用能力。在《图形面积的复习》中，教者采用了树形板书结构，这种板书一枝主干，数枝分枝，枝条精练，提纲挈领，树立了化繁为简的思想。它由“根”追到“枝”：图形的面积计算为什么从最简单的长方形入手？因为长方形最容易摆出多少

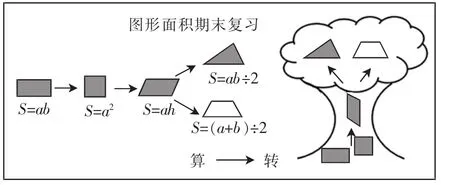
个面积单位，所以由简到繁，可以推导出平行四边形、三角形、梯形等的面积计算公式。理清了这样的结构关系，再由“枝”溯到“根”：研究发现梯形面积可以算遍所有图形的面积，既然梯形面积计算公式可以算所有图形，为什么到计算具体图形时又用具体图形面积去计算，这个回马枪式的设计体现了结构中具有统一的整体性，更有结构的独特性。板书正是有了结构、有了关联、有了比较才上出了数学的辩证法，也就是多样性下的统一性、统一性下的多样性。

同样在《运算律》的板书中，教者将运算律的教学从一年级看图写两个加法算式引入，带领学生经历“感知特征—形成猜想—举例验证—解释说明—得出结论”的整体过程，潜移默化地渗透科学探究方法。

还原学生数学学习本来的样子，需要我们教师怎么做？我想整合教学很重要，这就需要我们教本质、教结构、教过程、教思想。当我们站在学生的角度，让“板书结构化”的渗透成为一种自觉时，必然能改变教师的思维方式，激发学生强大的学习动力。当然，板书结构还可以打开、迁移：结构打开有大结构、小结构；结构迁移有知识内容结构、逻辑思维结构、算法算理结构、数学思想结构、思维方式结构等。这些，需要我们对“板书结构化”进行不断的实践与研究。♪