“平方差公式”的教学设计与分析

梁贻勤

【摘要】教师在教学“平方差公式”时要利用大量的素材，让学生通过探究学习，发现规律、理解公式的现实意义；注重公式的本质教学，加强拓展训练，以“提升学生思维，培养应用能力”为教学目标。

【关键词】平方差公式 素材 本质 训练

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）03A-0125-02

“平方差公式”的学习建立在有理数运算、整式分式运算、一次方程及乘法等知识的基础之上，是从一般到特殊的认知规律的范例。学习平方差公式，不仅可以简化整式的乘法运算，还可以为后续的公式学习提供借鉴。

对于平方差公式的教学，教师需要遵从学生的认知规律，首先利用丰富的教学素材，激发学生的兴趣，使学生发现规律，然后把握公式的核心，帮助学生从本质上理解公式，最后开展深化练习，使学生充分掌握公式。

一、利用素材，探究学习规律

数学从某种意义上来说是一门特殊的学科，数学知识是从具体的情境中总结出来的，是从众多对象中发现的共性规律。教师在教学中要做好引导工作，给学生提供充足的素材，帮助学生发现规律，让学生产生归纳意识，实现从自发思考到自觉思考的过渡。

例如，在教学“平方差”时，可以进行如下设计：

（1）一位狡猾的地主将一块边长为a的正方形土地租借给李老汉耕种。第二年，地主提出把土地纵向增加5米，横向减少5米，土地租金不变。你认为李老汉是否吃亏？可以用怎样的数学式子来表示？

（2）计算（p+q）（p-q）和（2x-1）（2x+1），你从中可以发现什么规律？

将生活中的情景作为课堂引入可以充分激发学生的学习兴趣，让学生经历数学建模的过程并从中总结出数学规律。

接下来教师可以增设满足平方差公式的形象素材，让学生运用总结的规律进行填空，进一步认识数学规律，增加教学意义。笔者给学生出示了如下例题。

运用上述式子的规律进行填空：

（△+☆）（△-☆）=_________________；

（月+亮）（月-亮）=_________________；

（X+Y）（X-Y）=_________________；

（□+○）（□-○）=_________________。

学生借助算式总结规律，教师引导学生运用规律进行形象化的图形填空，使得学生进一步了解平方差公式的结构特点，学生体验从发现规律到使用规律的过程，也可以充分认识到平方差的实际意义。

新知的学习需要教师引入大量的教学素材，为学生的学习搭建平台。教师在引入素材后要基于知识生成的逻辑规律来排列组合，通过引导设问，帮助学生建立对平方差的认识。

二、数形结合，揭示规律本质

数学知识的学习要透过表象深入本质，课堂教学也应该以揭示数学规律的本质为出发点，引导学生探究知识的本源。在教学平方差公式时，教师要从公式的本质出发，结合自己的教学经验，将自身对知识的体验与认识采用合理的方式传达给学生，帮助学生深刻体会知识的核心思想。

平方差公式是学生在学习了“单项式乘以单项式”“单项式乘以多项式”以及“多项式乘以多项式”之后学习的乘法公式，它是“多项式乘以多项式”的一种特殊情形。笔者认为，将平方差公式作为一个特定的公式加以学习的原因如下：它符合公式的便利特征，可简化运算；学习平方差公式的过程可为后续的学习提供知识基础，如之后将要学习的“公式法分解因式”“分式的化简”等；可以借鉴平方差公式的探究过程及方法学习“完全平方公式”。

（一）内容形式

内容形式是掌握公式的基础，课堂教学要注重平方差公式的内容表达。平方差公式指“两数之和与这两个数之差的乘积等于这两个数的平方差”，用数学符号可以概括为（a+b）（a-b）=a2-b2，教师在实际教学中可以借助形象的图形来帮助学生理解（如图1），图形可以清晰地揭示平方差公式的合理性。学生对于抽象数学公式的认识还较为模糊，教师在教学中通过“文字描述”“符号概况”“图形表达”三种方式来揭示公式的本质，对于学生理解及掌握知识有极大帮助。

（二）数学思想

在探究数学问题时需要对问题的某些特例进行深入研究，即数学中的“特殊化”思想。教师在教学“平方差公式”时要注意向学生传达该公式是建立在“多项式乘以多项式”的基础之上的，它不仅是数学公式，同时还体现了从“一般”到“特殊”的研究方法。如教师在教学中将平方差公式进行拆分，（a+b）（a-b）=a2-ab+ab-b2=a2-b2，让学生分析左右两边的结果，发现其中的规律，即左边为两数之和与两数之差的乘积（多项式乘以多项式），右边为两数的平方差。这样的教学方式，不仅可以使学生充分理解并掌握平方差公式，还可以帮助學生理解公式的特殊化思想。

与此同时，教师在教学中还应向学生传达归纳思想，平方差公式是在观察一系列具有相同结构特征的“多项式乘以多项式”后，通过归纳该“结构特征”，总结出来的相同的规律。教师在教学中可以设置图2所示的多项式，让学生通过计算，发现算式的结构特征并总结规律，从而深刻理解归纳思想。

三、拓展运用，深化规律训练

“先学后做”的教学理念要求课堂教学应该是“知识学习”与“训练巩固”相结合的完整过程，必要的拓展训练可以使学生改变原有的“程序性”记忆陋习，知识的讲授不应该培养机械思维，技能的形成要通过多次的拓展训练。在教学“平方差公式”时也需要进行针对性训练，帮助学生掌握公式，形成灵活变通的思维方式，学以致用。

例如，教师为进一步培养学生解题思路设计如下两道题：①98×（-102）；②（x+2）（x-2）-（x-1）（x+5）。教师首先引导学生对算式进行整体观察，确认是否可以采用平方差公式进行简便计算，可进行变形转化的题目则将其变形，不能采用公式的题目要严格按照多项式乘法进行求解。第一题可以使学生形成“两数相乘转化成两数和与两数差的乘积的形式，然后运用平方差公式计算”的解题思路，该题目的设置可以帮助学生深化转化思想，理解数式的通性。第二题是平方差公式与一般多项式乘法的综合题，对于培养学生的综合解题能力极为有利。教学平方差公式还应该注意提升学生的逆向思维，教师可以设置这样的填空题：①（5x+2y）（ ）=25x2-4y2；②（ ）（ ）=81-a2。通过训练，学生从正反两方面灵活运用平方差公式，从而深刻理解了公式的结构特点，发散了思维。在拓展应用的练习阶段，教师则有必要结合生活实际设计问题，例如：小红家有一块呈“L”形的菜地（如图3），现要将该菜地分成面积、形状相同的两部分并种上不同的蔬菜，请你来帮忙设计，并计算该菜地的总面积。该题目的设计与平方差公式的几何意义相一致，学生通过求解可以体会到运用平方差公式解决实际问题的便利，体会“数学源于生活又服务于生活”的思想。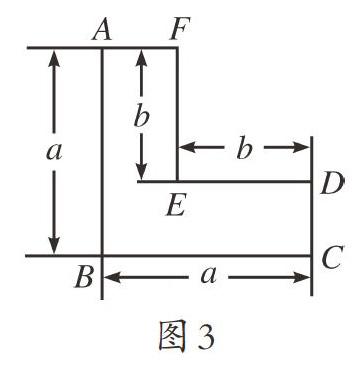

学生在学习过程中过度模仿容易造成思维定式，缺乏针对性或者简单的重复训练则会让学生陷入机械训练。教师要针对学生的思维开展针对性训练，使学生进一步理解平方差公式，拓展思维，提升学生的解題能力；同时需结合生活实例，培养学生的应用思想，为学生之后的学习打下基础。

总之，平方差公式是多项式乘法运算中特殊形式的多项式乘法公式，它对于简便运算具有极大的帮助；“平方差公式”的教学可以为之后的公式学习提供教学参考，教师在教学时应加以重视。教师在教学中应有效利用素材，开展探究学习，帮助学生发现规律，感知平方差公式；揭示公式本质，让学生从内容和思想上理解公式的核心；开展拓展练习，培养学生的发散思维，提升学生的应用能力。

【参考文献】

[1]周进荣，储东花.牵住课堂教学的“牛鼻子”——以“平方差公式”教学目标的叙写为例[J].中学数学，2015（12）

[2]涂爱玲，梁艳云.代数类新知课“平方差公式”四环节教学模式例析[J].广西教育，2016（48）

（责编 刘小瑗）