《平均数》教学重在探“理”寻“法”
2018-05-29李英婷
李英婷
【摘要】本文提出以“平均数”的数理和算法为重点,寻找算法与算理的融合,挖掘平均数的本质特征,让学生深入理解平均数的概念,掌握求平均数的方法。
【关键词】《平均数》 数学本质 探理寻法
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2018)03A-0099-02
“平均数”是分析数据的重要的工具,常用来对统计对象进行一般水平的描述,是一个居中位置的数据统计量。在“平均数”的教学中,学生很容易掌握“平均数”的计算方法,但是如何让学生理解平均数的概念,培养学生数据分析的能力,才是教学的重点和难点。笔者在教学时主要从以下三点进行尝试。
一、从儿童视角出发,探”平均”数理
对小学生来说,概念的习得需要经历一个完整的过程,这个过程包括三个阶段:弄清它是什么,怎么能够学会,知道它怎么用(即理解本质,掌握方法,学会应用)。平均数的学习要突出“平均”这个概念的数理,让学生把握本质所在。如,小强在50米跑中分别跑出了15秒、14秒、12秒、10秒和14秒的成绩。在他填写自己的成绩时,他犯难了,到底该填几秒呢?教学时,笔者通过三个层面进行引导,强化学生对“平均数”概念的理解。
(一)加强快慢对比,探求中间值
学生已经积累了关于快慢的经验,笔者以这个经验为抓手,引导学生从填写极端数15秒入手,发现偏慢;填写10秒,发现又偏快,进而引导学生寻找偏向中间值的不快不慢的数据13,这不仅是引导学生根据数据对比后分析得出的结果,更是帮助学生整合思维得到的结果。学生用自己对数据分析的不快不慢的这个经验,找到了平均数概念的本质特征,也就是说,13这个数据能够反映出这组数据中一个集中的趋势,代表这组数据的一般水平。由此学生进一步理解了平均数的内涵:能够代表这一组数据的基本特征。
(二)激活认知冲突,认识到平均数也可以是虚拟的数
在整个教学过程中,学生根据偏快和偏慢进行分析判断,认为“不快不慢”的13秒,才是一个能够体现小强真实水平的成绩。但是13秒这个数据并没有出现,让学生产生了认知冲突。于是,笔者从不同层面引导学生思考这个数据出现的可能性。从学生认为“可能”到认为“可能性很大”,经历了一个从现实到需求之间的冲突,由此学生发现,平均数也可以是一组数据中没有出现的一个数。也就是说,平均数的另一个特征就是可以是一个虚拟的数。
(三)层层追问,让学生体会“平均”的本质内涵
在带领学生探寻“平均”的本质内涵的过程,就是一个不断追问,让学生不断梳理的过程。从一开始的数据偏慢,到后来的偏快,最后到找出不快不慢的数据,整个过程笔者没有给出明确的答案,而是不断地追问,让学生一点点理解,并用自己的体会来诠释“平均”这个概念的本质属性,从而建立了具有鲜明儿童表征的属性——刚刚好。
二、以操作为核心,寻“算法”之根
在上一轮的讨论中,学生根据预习,已经知道平均数的算法是将一组数据相加除以数据的个数得到。为此,笔者展开引导:有同学将五个数相加除以5,算出小强的平均成绩是13秒。那么这个13和这一组数据有没有关系呢?你能找出13藏在哪吗?
笔者出示学具,让学生在黑板上移动学具。(如下图)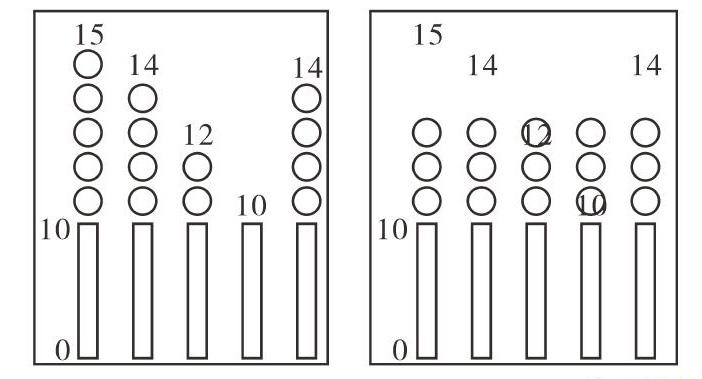
学生将一个14,一个12变成了两个13;将15移了2个给10,再将14移1个给10,又变出了三个13,这样就将这5个高高低低的数字拉平,变成了五个13。此时笔者又引导学生分析这五个数字。学生发现15最慢,10最快,12偏快,只有13不快不慢,刚刚好。笔者追问:仔细想一想,这个13有哪两个特点呢?学生认为:一是没有在数据中出现,二是它能够代表小强的水平。笔者继续追问:可是这个成绩,小强没有跑出来过,是怎么得到的呢?学生认为是通过以多补少匀出来的。至此,有学生提出:平均数不一定非要出现在一组数据中,它可以不出现,也可以出现。
求平均数的算法,对于三年级的学生来说并不复杂,但是对于平均数这个概念而言,不但要让学生知道算法,还要知道为什么这样算,这才是教學的难点,也就是要引导学生在算法上去寻根。
三、以巩固为基础,拓“运用”之道
学生理解并掌握了平均数的数理和算法后,笔者由浅入深,层层引导学生进入巩固运用环节:7和8两个数的平均数是多少?1、3、8这三个数的平均数是多少?你是怎么算出来的呢?在学生顺利解答这几个问题后,笔者展开拓展:一条河平均水深5米,请问这条河最深有几米?为什么?学生认为最深可能会是7米,也可能是10米……此时笔者继续追问:那如果把这条河修整一下,变成平均水深一米。小强身高一米,走过去安全吗?学生认为不安全,虽然平均水深是一米,但最深的地方有可能会超过一米。
通过设计这样的练习,引导学生理解平均数的“虚拟”特性。
总之,求平均数的教学并不是让学生单纯地掌握求平均数的算法,而是要让学生根据已有经验,探知平均数理,寻得算法之根,从而将已有经验与所学新知有机结合,真正理解并掌握平均数这个概念。
(责编 林 剑)
