海上突发事件下的航道通航效率分析

马 峰,胡智辉，潘家财，梅 强

(集美大学航海学院，福建 厦门 361021)

0 引言

海上交通突发事件是指由自然的或人为的不可预见因素造成的航道通航能力降低的非正常事件[1]，常见的海上突发事件有恶劣天气、交通管制和交通事故等。突发事件会引起交通拥堵，造成船舶排队，等待，从而降低航道通航效率，因此如何量化突发事件下航道拥堵的时空范围成为海事相关部门需考虑的问题。

在交通拥堵研究领域内，交通波理论的应用比较成熟。文献[2-3]利用交通波理论研究交通拥堵的形成条件，从而探索交通流产生拥挤的内在规律；文献[4-6]对船舶交通流的聚集和消散过程进行分析，建立了船舶交通波时空拥堵模型，量化了船舶通航效率；文献[7-9]从交通瓶颈，交通事故等方面对交通流运行状态进行分析，建立拥挤时空模型，计算出拥挤长度和等待时间，最终确定影响范围。本文通过调查厦门港超大型船舶进港方式，利用交通波理论定量计算出最大排队长度和阻塞时间，为厦门港管理部门在制定相关通航计划时提供参考依据。

1 交通波理论基本原理

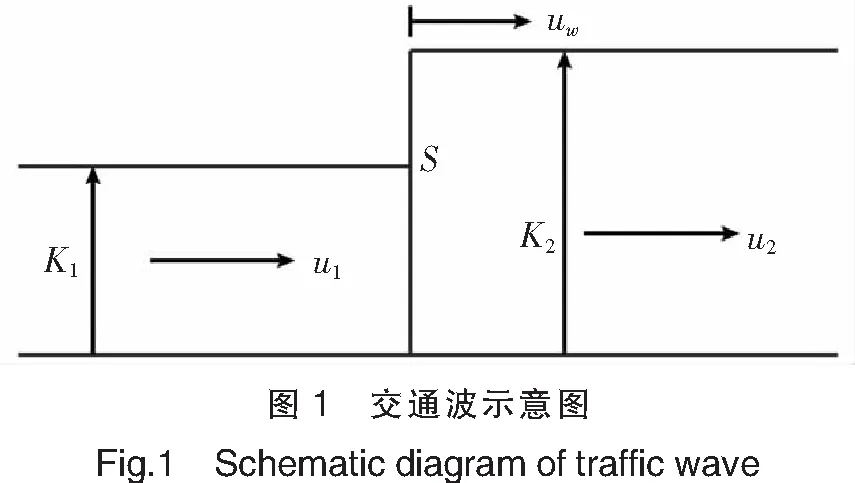
假设航道内有两个相邻的船舶流,如图1所示，密度分别为k1和k2，船舶交通流平均航速分别为u1和u2，相邻船舶流临界处将产生一个波阵面S，其速度为uw，即交通波速度。当uw>0时，交通波方向与船舶交通流前进方向相同；当uw<0时，交通波方向与船舶交通流前进方向相反。当k1k2时，船舶交通流密度降低，船舶加速离开，表明交通波为消散波。

根据质量守恒定律，时间t内波阵面S左侧流出船舶数量等于右侧流入船舶数量，即：k1(u1-uw)t=k2(u2-uw)t，解得：

uw=(k1u1-k2u2)/(k1-k2)。

(1)

式(1)为交通波的基本方程。

假设船舶交通流符合格林希尔的速度-密度线性关系：u=uf(1-k/kj)，其中：uf为船舶自由流速度(km/h)；kj为船舶交通流阻塞密度(艘/km)。引入船舶交通流标准化密度η，记ηi=ki/kj，则有

ui=uf(1-ηi)，

(2)

解得

ηi=1-ui/uf。

(3)

将公式(2)代入公式(1)，可得：

uw=uf[1-(k1/kj+k2/kj)]，

(4)

uw=uf[1-(η1+η2)]。

(5)

将公式(3)代入公式(5)，可得交通波另一表达式：

uw=uf[1-((1-u1/uf)+(1-u2/uf))]。

(6)

2 突发事件时空影响模型

本文以厦门港20万t级以上的超大型船舶进出港为例，建立时空影响模型。由于厦门港较少停靠超大型船舶，在相关的安全保障措施上并不完善，为安全起见，厦门港海事部门对此类船舶进港实施单向通航。

2.1 船舶交通流时空影响分析

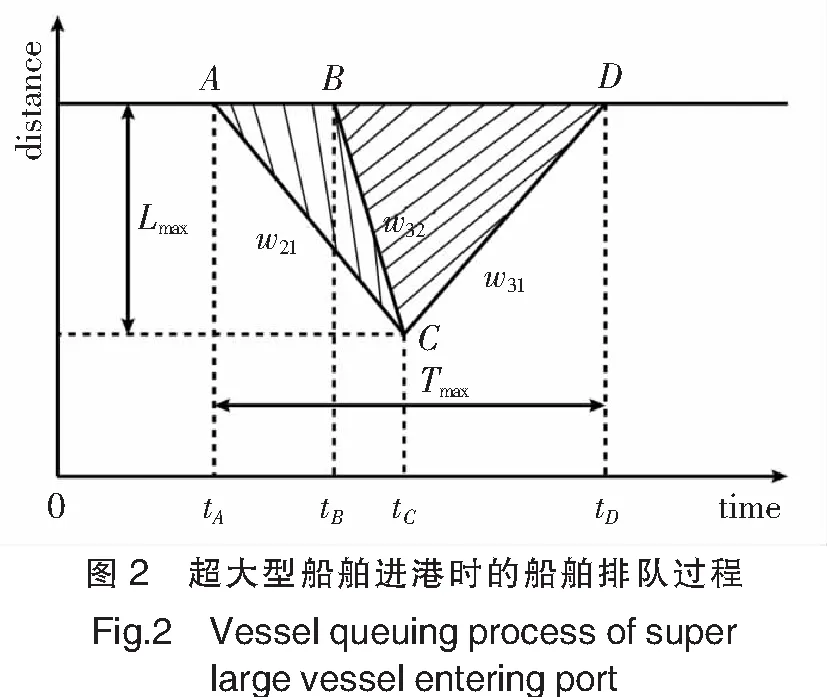
根据交通波的船舶特性，超大型船舶进港时船舶集散过程如图2所示。在0至tA时段没有发生突发事件，航道内船舶以正常航速航行；在tA时刻超大型船舶进港，为保证航行安全，港内实行单向航行，出港船舶被禁止通行，减速进入待航区，因此在待航区形成一个集结波(波速为w21)；在tB时刻，超大型船舶靠港成功，海事管理部门通告解除单向航行，出港船舶将加速驶离港口，产生一个消散波(波速为w32)；在tC时刻，消散波与集结波相遇，形成新的交通波(波速为w31)；在tD时刻，封航影响全部消除，航道恢复了正常通航。从图2中可以看出，超大型船舶在航道航行的时间为tB-tA，即单向通航时间，超大型船舶进港单向行驶造成的最大排队长度为Lmax，最大排队时间为Tmax。最大排队长度和最大排队时间是影响航道通航效率的两个主要指标，最大排队时间和最大排队长度越大，表明其航道通航效率越低，因此海事管理部门在超大型船舶进港时，应采取相应措施，提高其通航效率。

2.2 时空影响模型的建立

突发事件产生的交通波分三个阶段，分别为集结波阶段、消散波阶段和相遇波阶段。为合理求出最大排队长度及阻塞时间，假设航道内的船舶速度与密度关系符合格林希尔模型。

1)集结波阶段

根据公式(6)可得，集结波波速w21为：

w21=uf[1-(η1+η2)]=uf[1-((1-u1/uf)+(1-u2/uf))]。

(7)

式中：uf为船舶自由流航速，u1为航道船舶平均航速；u2为单向通航后的船舶航速，因此u2=0。故公式(7)又可以变换为：

w21=-(uf-u1)。

(8)

2)消散波阶段

w32=uf[1-(η2+η3)]=uf[1-((1-u2/uf)+(1-u3/uf))]。

(9)

式中：u3为船舶刚启动航速，一般很小，可以忽略不计，因此公式(9)可变换为：

w32=-uf。

(10)

3)相遇波阶段

(11)

通过求出三种波速w21、w32和w31，结合图2中三种波速之间的关系，可以求出最大排队长度Lmax和最大排队时间(阻塞时间)Tmax。其中最大排队长度Lmax为：

Lmax=[|w32×w21|/|w32|-|w21|]×(tB-tA)。

(12)

式中：tB-tA为超大型船舶在航道航行时间(单向通航时间)。

阻塞时间Tmax公式为：

Tmax=Lmax/|w21|+Lmax/|w31|。

(13)

3 算例分析

以船长400 m的超大集装箱轮AL DAHNA靠海沧码头为例，其航迹图如图3所示。该轮在2017年2月26日中午12：30左右过九节礁，13：00左右上引水，13：30左右靠近码头前沿，历时约1 h。统计厦门主航道进出港船舶速度，获得主航道船舶平均航速u1为12 kn，船舶最高限速15 kn作为船舶自由流航速uf。根据公式(8)可求得集结波波速w21为：

w21=-(uf-u1)=-(15-12)=-3 (kn)

通过式(10)和式(11)可求得消散波波速和相遇波波速分别为w32=-15 kn和w31=9 kn。利用式(12)可以求出最大排队长度Lmax，其中w21和w32已经求解，(tB-tA)为单向封航时间，即超大集装箱轮AL DAHNA 靠海沧码头时间1 h，所以最大排队长度Lmax为：

Lmax=[|w32×w21|/(|w32|-|w21|)]×(tB-tA)=45/9×1=5 (n mile)。

根据式(13)可以求得最大排队时间Tmax为：

Tmax=Lmax/|w21|+Lmax/|w31|=5/3+5/9=2.22 (h)

4 分析及结论

基于交通波理论，以厦门港超大型船舶进港为例，建立了超大型船舶进港单向通航时空影响模型，定量计算出港船舶最大排队长度和阻塞时间。为减少单向通航带来的影响，建议：

1)最大排队长度与单向通航时间成正比，因此在安全条件下应减少超大型船舶在航时间，从而减少最大排队长度和阻塞时间；

2)交通波波速与在航船舶平均航速有关，因此超大型船舶在进港单向航行时应提前对出港船舶航速进行减速调控，以减少最大排队长度和阻塞时间；

3)拓宽航道宽度，实现双向通航。

[]

[1]马剑,李文勇,王振.城市交通突发事件的影响范围研究[J].公路与汽运,2012(4):67-70.

[2]QI H,SONG.On the critical conditions of traffic jams[J].Journal of Southeast University(English Edition),2011,27(2):180-184.

[3]SINGH V P.Kinematic wave theory of overland flow[J].Water Resources Management,2017,31:1-14.

[4]白响恩,肖英杰,孙玉萍,等.基于交通波理论的北槽深水航道通航效率[J].中国航海,2014,37(1):61-65.

[5]孙玉萍,吴善刚,肖英杰,等.基于交通波理论的混合水域通航效率研究[J].水运工程,2013(12):126-130.

[6]卢升荣,刘瑶.极端水位对长江中游船舶交通流特征的影响[J].重庆交通大学学报(自然科学版),2017,36(3):103-107.

[7]王殿海,景春光,曲昭伟.交通波理论在交叉口交通流分析中的应用[J].中国公路学报,2002(1):96-99.

[8]任作武,朱守林,戚春华.基于交通波理论的高速公路瓶颈路段排队分析[J].森林工程,2014,30(1):134-136，173.

[9]余贵珍,刘玉敏,金茂菁,等.基于交通波的高速公路事故的交通影响分析[J].北京航空航天大学学报,2012,38(10):1420-1424.DOI：10.13700/j.bb.1001-5965.2012.10.030.