基于相似系数的产品设计时间估算方法
2018-05-28杨续昌赵永满谷梦瑶李玉林宋海草
杨续昌,赵永满*,谷梦瑶,李玉林,宋海草
(1石河子大学机械电气工程学院,新疆 石河子 832003;2重庆大学机械工程学院,重庆 400044)
产品的设计时间占了产品开发总时间的75%左右,并且设计阶段所需费用仅占产品总成本的6%-7%,但对其的影响却高达80%[1],同时设计阶段对产品的使用性能、可靠性和可维修性等也起着决定性的作用,因此,产品设计时间的准确预测对企业产品开发过程的规划和控制尤为重要。然而产品设计活动是典型的智力工作,影响因素多且影响过程复杂,致使设计时间的量化与准确预测难以实现,因此企业界应用较多的是经验分析法和因素分析法等传统的设计时间预测方法,但其主观性较强而致使预测偏差较大[2]。为此,探究科学合理的精确度的设计时间预测方法成为了企业急需解决的问题之一。
近年来已有学者对设计时间预测方法进行了一定的研究。Cho S H等[3]假设产品设计活动时间服从三角分布,并基于此运用仿真技术建立了资源约束下的产品开发时间模型;Zhang K L等[4]针对设计时间影响因素中存在语言型变量的问题,建立了基于高斯过程元模型设计时间模型;Yan H S等[5]通过设计结构矩阵分析信息流的特点,而后据此构建时间估算模型以预测每项设计活动的时间并汇总得到整个产品开发时间;Xu D等[6]提出了一种模糊神经网络模型来估算产品设计时间;Yan H S等[7]将模糊回归理论与ν-SVM应用于产品设计时间预测,提出了Fν-SVM模型。以上研究虽然在设计时间预测方法、设计时间估算模型构建等方面进行了积极探索,但我们认为存在以下不足:
(1)部分设计时间预测方法受自身因素影响,易造成较大偏差,比如文献[3]在模型建立中会受到假设的限制;
(2)部分设计时间预测方法复杂度高、不易操作,难以在企业实施和推广,比如模糊神经网络技术[6]和Fν-SVM模型[7];
(3)应用上存在局限性,比如IK-KA模型[5]适合于小样本情况下的设计时间预测。
陈友玲等[8]运用相似性原理,提出了基于工序相似系数的工时计算方法,为产品设计时间估算方法研究提供了新思路。
理论上,不同事物之间在一定程度上存在某些共同的或相似的特征或属性。贡智兵[9]认为在一般机械类产品中大约70%的功能部件间存在着功能和结构上的相似性。据统计,新产品开发中完全重用的零部件高达40%,改型设计后重用的零部件约占40%,然而完全创新的零部件却不足20%[9];同时在企业的工具、生产计划和产品设计等中存在着的大量相似性,若对其加以正确的利用,将有助于降低产品开发的复杂度和提高产品开发的效率[10];再者,在工程实际中最常见的是根据客户订单要求进行的改型设计,即企业首先在产品库中检索和目标产品最相似的历史产品,然后在它的基础上进行局部的修改,目前这种设计方式在企业诸多的新产品设计中占了约80%的份额[10]。
基于此,面向改型产品设计,本文创新性地提出一种基于产品设计相似系数的设计时间估算方法。首先,简单分析了产品设计时间影响因素;其次,详细说明了基于产品设计相似系数的设计时间估算过程,并运用三角模糊数和灰色关联分析法构建产品设计相似系数的计算模型;再次,运用Matlab软件确定产品设计相似系数与设计时间之间的关系函数;最后通过范例与已有算法的对比分析,验证该方法的合理性和可行性。
1 设计时间影响因素分析
郭波等[11]认为在本质上产品设计时间估计属于非线性回归估计问题,而作为估计模型输入变量的时间影响因素种类也很多;谷梦瑶等[12]在国内外学者研究成果的基础上,归纳总结得影响设计时间的因素一般为产品特征、设计过程、设计环境和设计者这4个方面;许多研究者[4-7,12-13]皆以产品特征、设计过程、设计环境和设计者作为其设计时间估算模型的输入变量,而且这些因素与设计时间之间的关系是高度非线性的。因此本文也选择以产品特征、设计过程、设计环境和设计者作为影响设计时间的因素。
对于同一企业而言,设计环境通常保持不变,郭波等[11]通过“面向产品设计的脑力符合及时间研究实验”证明了产品特征和设计者因素对设计时间存在显著地影响。同时谷梦瑶等[12]认为在企业实际的产品设计活动中,随产品类型的不同而变动幅度最大的是产品特征因素,而其他三方面因素则变动幅度较小或保持不变。因此本文主要考察产品特征因素,其一般包括产品形状、结构、尺寸和精度等,但是具体细分情况需要具体化到各个产品。
2 基于设计相似系数的产品设计时间估算
2.1 基于相似系数的产品设计时间估算过程
建立基于产品相似度的设计时间估算路线,如图1所示。
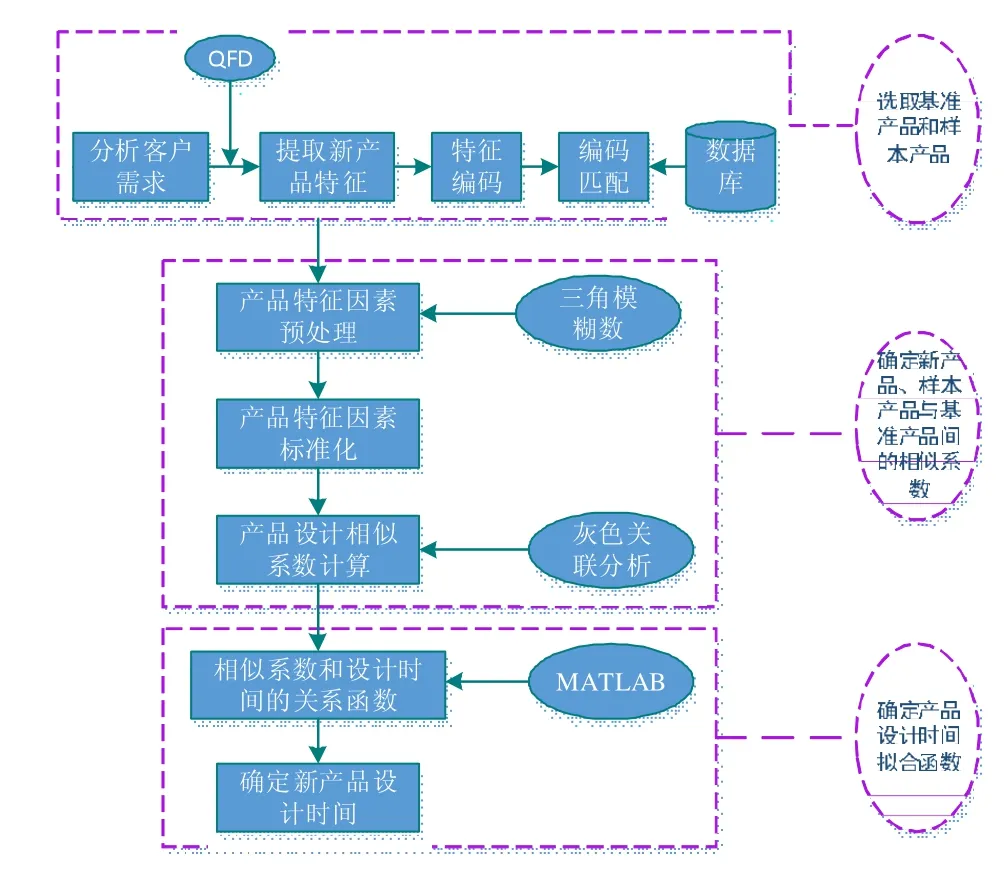
图1 基于相似系数的产品设计时间估算路线Fig.1 The design time estimation route based on similarity coefficient
第1阶段:由谷梦瑶等[12]研究成果知,利用质量功能配置(QFD)技术可以将客户需求转化为产品特征,再由陈友玲等[8]研究结果知,运用编码技术可实现工时的快速检索,进而有助于工时定额的快速制定,因此,本文运用QFD技术提取产品特征,并引入编码技术对产品特征进行编码,然后在企业历史产品信息数据库中对新产品产品特征进行编码匹配,并基于相似性原理选取若干同类型的历史产品,最后从已选历史产品中选择结构、造型等最简单、设计时间已知且精确的样本作为基准产品,剩余的作为样本产品。
第2阶段:结合基准产品、样本产品和新产品的产品特征信息,首先运用三角模糊数对产品特征因素进行预处理,然后为消除量纲的影响,对产品特征因素进行标准化处理,最后运用灰色关联分析分别计算新产品、样本产品与基准产品的产品设计相似系数;
第3阶段:运用Matlab软件进行拟合分析,确定产品设计相似系数时间和设计时间之间的关系函数,进而构建基于产品设计相似系数的设计时间估算模型,然后输入新产品与基准产品的产品设计相似系数,以估算新产品设计时间。
2.2 确定产品设计相似系数
2.2.1 产品特征因素预处理
因为产品特征因素中既包含定量因素又包含定性因素,所以实际收集到的产品特征数据往往具有一定的不确定性和模糊性[14]。模糊数可将模糊的、不确定的语言变量转化为确定的数值,并且这种表示形式更能体现数据原貌。而在众多模糊数中,三角模糊数是最易于运算并且其实际应用较为广泛[14],其中文献[15]采用三角模糊数对客户需求进行量化处理并取得了良好的应用效果。因此本文采用三角模糊数对产品特征因素值进行转换。
2.2.1.1 定量特征因素
简单来说,定量特征因素就是数量化的产品特征因素,如尺寸、主要功能数、重量等[12]。经分析知,产品定量特征因素的表达一般包括以下4种方式[15]:
(1)模糊数值型表达,如大于α、小于α、大约是α等。
若产品某项特征为“大于α”,则其相应的三角模糊数为(α,α+τ,α+σ);若为“小于α”,则其相应的三角模糊数(α-σ,α-τ,α);若为“大约是α”,则其相应的三角模糊数(α-σ,α,α+σ)。其中0<τ<σ为经验参数,可以由企业设计人员或产品设计专家依据自身产品设计经验并结合具体产品确定。
(2)区间数值型表达,如在a和b之间。
若产品某项特征为“在a和b之间”,则其相应的三角模糊数为
(3)模糊型表达,如重量轻、价格低等。
若产品某项定量因素为模糊型表达,则可先由企业设计人员或产品设计专家依据自身产品设计经验并结合具体产品为其设定一个区间数,然后再依据区间数值型表达进行转换。
(4)精确值表达,如尺寸的大小,主要功能数量。
2.2.1.2 定性指标
定性特征因素是描述性特征因素,如可靠性、润滑状况等,其表达更多地是模糊语言形式,比如可靠性较高、润滑状况良好等[12]。假设定性特征因素共k项,则其可表达为{g1,g2,……gk},其中gh(1≤h≤k)包含Lh个离散的由模糊语言表示的程度等级,则其等级集为[15]。而若gq为第q个程i度等级,其中 1≤q≤Li,那么其三角模糊数θ~q为:

其中f=min{max[(2q-3)e,0],1},e=1/[2(Li-2)],t≥1 且为整数。
2.2.2 产品特征因素标准化
为了消除由于定量特征因素间量纲和数量级的差异而造成的影响,需要对产品特征因素进行标准化处理,使其成为无量纲、无数量级差别的形式[8]。以下根据产品特征因素的性质,采用不同方法将,fij,f+ij]标准化为,i=1,2…,n,j=1,2,…,m,
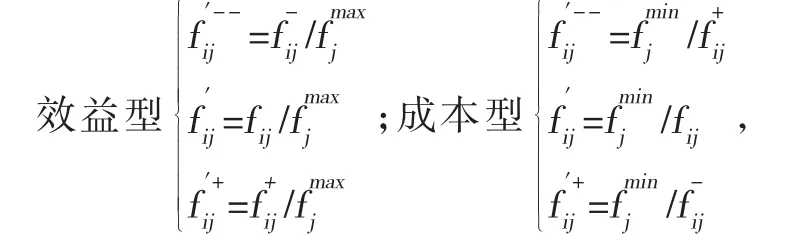
其中
2.2.3 产品设计相似系数计算
灰色关联分析是一项通过计算关联度来描述系统因素间关系密切程度的成熟方法[16]。其对数据的样本量和分布规律要求不多[17],这有效的解决了因产品定制程度较高而使得可用历史样本较少的问题。而且其计算过程简单易懂,便于在企业内实施和推广。因此本文采用灰色关联分析来计算产品设计相似系数。
假设基准样本S0的产品特征因素为

则根据灰色关联分析理论知,基准样本S0和历史样本Si关于指标Cj的灰色关联系数为

式(2)中:ρ∈[1,0]为分辨系数,一般取 0.5,i=1,2,…,n,j=1,2,…,m。
由于产品特征因素转换为了三角模糊数,则其距离根据三角模糊数的定义[14]知,

则基准样本S0和历史样本Si的相似关联度为

式(3)中:wj为产品特征因素权重,由企业设计人员或产品设计专家依据自身产品设计经验并结合具体产品,运用层次分析法所得。
3 基于产品设计相似系数的设计时间估算模型
3.1 模型构建
科学实验和工程应用中,常需要确定两个或多个变量是否相关以及其相关程度等,并选择适当的数学函数来描述变量间的关系以揭示其内在联系[8]。而Matlab的曲线拟合工具箱拥有一个可视化的图形界面和强大的曲线拟合功能,操作简单,能快速而简单的解决计算复杂或大量数据的情况[18]。因此本文选用Matlab曲线拟合工具箱来确立产品设计相似系数和设计时间的关系函数。
3.2 模型论证
3.2.1 合理性论证
Zhang K L等[4]提出了一种基于高斯过程元模型的设计时间估算方法,并通过算例分析证明该模型优于已有的2种模糊神经网络模型;商志根、严洪森[13]提出了一种基于嵌入知识的核近似的时间预测方法,并通过实例证明了该方法具有较好的预测效果。考虑到这2种设计时间预测方法[4,13]的合理性和准确性,本文选用这2种方法和本文方法共同进行合理性实验。若证明本文方法所得设计时间与上述两种方法所得设计时间基本符合,且没有异常情况,则说明本文方法是合理的、可行的。
3.2.2 有效性论证
运用这2种方法估算产品设计时间,第1种方法为本文方法,第2种是企业原有设计方法。若证明第1种方法所得设计时间比第2种的更接近实际设计时间,则证明本文方法所得设计时间更为准确,由此证明本文方法的有效性。
4 算例及分析
A企业是国内大型齿轮油泵生产商,主要承接各种机械零部件的研发、设计、制造等业务。某客户要求设计并生产一批新齿轮油泵M,并要求提供较为具体的交货期。同时在多年的生产设计中,公司积累了大量齿轮油泵的设计案例,因此新齿轮油泵M的设计类型为改型设计。而为了估计产品交货期并安排后期的生产活动,企业需要预先确定新产品M的设计时间。然而通过现场调研发现A企业目前在设计时间预测方面的主要问题为:(1)A企业对产品历史数据库的利用率很低;(2)目前企业所采用的设计时间预测方法为判断分析法,即设计管理人员依靠经验分析预测设计任务所需的时间,而通过分析历史数据知,该方法主观性强,误差率较高。这些问题导致所制定的设计时间偏差较大,使得企业无法合理的安排生产。因此A企业亟需一种新的产品设计时间的预测方法来解决当前现状,而且企业目前积累了大量的历史齿轮油泵的产品特征、设计时间和设计团队等等信息,这为基于产品相似系数的设计时间估算方法的实施提供了有利条件。
4.1 新产品特征提取和样本产品选取
运用QFD技术提取新产品特征,如表1所示。然后对新产品特征进行编码,并在A企业历史产品数据库中进行编码匹配;基于相似性原理选取32组与新产品M相似且有完善而精确的设计时间数据的齿轮油泵实例,并从选择一个结构、工艺等最简单的实例作为基准产品;最后从剩余的31组中选择15组用于数据拟合分析,剩余16组用于模型验证。

表1 新产品特征Tab.1 Characteristics of new products
4.2 产品设计相似系数计算
对产品特征因素进行预处理,得产品特征三角模糊数,见表2。

表2 新产品和基准产品的特征三角模糊数Tab.2 Triangular fuzzy numbers of new products and benchmark products
对产品特征进行标准化处理后,运用公式(2)和(3)计算新产品设计相似系数为0.790,其中运用AHP法所得的产品各特征权重和运用公式(2)所得的新产品各特征的灰色关联度如表3所示。

表3 新产品各特征权重Tab.3 Weight of each feature of new product
4.3 模型构建
运用公式(2)和(3)依次计算15组拟合样本的产品设计相似系数,结果见表4,其中T为相应的产品设计时间。

表4 待拟合数据Tab.4 Data to be fitted
根据待拟合数据,运用Matlab对产品设计相似系数γ与设计时间T进行拟合分析,首先运用曲线拟合工具箱绘制两者的散点图,然后根据散点图依次选择多项式、高斯和傅里叶级数等函数进行曲线拟合。各函数对应的拟合度依次为0.2832(5次多项式)、0.883(3阶高斯函数)和 0.646(3阶傅里叶级数),其中拟合度表示模型预测结果与实际情况的吻合程度,拟合度越高代表所得函数模型的拟合精度越高。鉴于3阶高斯函数的拟合度最高,因而3阶高斯函数为本文方法的最佳拟合函数。而相应的拟合曲线如图2(图中纵坐标为设计时间,单位为小时;横坐标为产品设计相似系数)所示。

图2 相似系数与设计时间的拟合曲线Fig.2 Fitting curve of similarity coefficient and design time
根据Matlab输出结果知,产品设计相似系数γ和设计时间T满足以下关系:

式(4)中:α1=87.26,b1=0.4688,c1=0.01877,b2=0.5622,α2=41.28,c2=0.01499,b3=0.9419,α3=38.45,c3=0.6337。
将新产品M的产品设计相似系数输入公式(4),即可得到新产品M的设计时间为T=36.307h。
4.4 模型验证及分析
4.4.1 合理性论证
为了验证本文方法的合理性,由16组模型验证样本中随机选择8组,而后依次运用基于高斯过程元模型的设计时间估算方法、基于嵌入知识的核近似的时间预测方法和本文方法预测模型(由表4中的待拟合数据所得)估算样本的产品设计时间,计算结果如表5所示。表5中T为本文方法所得设计时间,T1为基于高斯元模型的设计时间估计方法所得设计时间,T2为基于核近似的设计时间预测方法所得设计时间,误差1为与间的误差百分比,误差2为与间的误差百分比。

表5 合理性论证数据Tab.5 rationality argument data
为了便于比较,将3种方法所得设计时间用折线图表示,结果见图3。

图3 三种方法对比图Fig.3 three methods comparison diagram
由表5和图3可知:
(1)本文方法所得设计时间T与基于高斯过程元模型的设计时间估计方法的平均误差百分比为4.087%,而其与基于核近似的设计时间预测方法的平均误差百分比为4.220%,两者均小于5%,属于可接受的范围。
(2)3种方法所得设计时间基本接近,且没有异常情况。由此说明本文方法所得设计时间是合理的。同时与上述2种方法相比,本文方法操作简单,易于理解。
4.4.2 有效性论证
由现场调研知,A企业的设计时间预测方法多为判断分析法,主观性较强,误差较大。为了验证本文方法所得设计时间对A企业是否有效,依据剩余的8组模型验证样本,分别采用A企业原有预测方法(判断因素法)与本文方法预测模型(由表4中的待拟合数据所得)估算样本产品设计时间,计算结果如表6所示。表6中T实为样本产品的实际设计时间,T为本文方法所得设计时间,T3为企业原有预测方法所得设计时间,误差3为T实与T间的误差百分比,误差4为T实与T3间的误差百分比。
由表6可知:本文方法所得设计时间T和产品的实际设计时间的T实的平均误差百分比为5.436%,而A企业原有预测方法所得设计时间T3与产品的实际设计时间的T实的平均误差百分比为16.843%,前者明显小于后者。
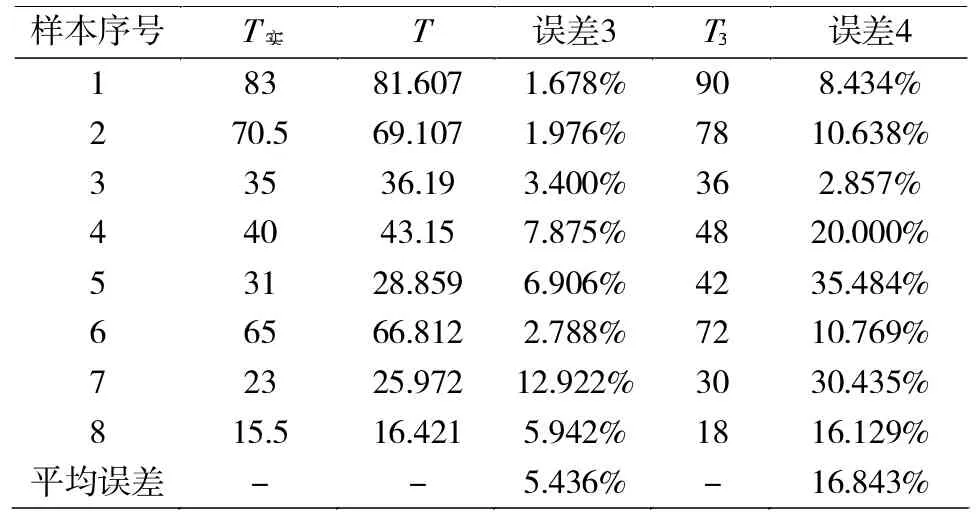
表6 有效性论证数据Tab.6 validation data
为了便于比较,将2种方法所得设计时间用折线图表示,结果见图4。
图4显示:本文方法所得设计时间T比A企业原有预测方法所得设计时间T3整体上更接近与产品的实际设计时间T实。由此说明本文方法精确度更高,具有一定的实用价值。另外,与A企业原有预测方法相比,本文方法客观性更强,准确性更高。

图4 两种方法对比图Fig.4 comparison of two methods
5 结束语
(1)针对于企业现有产品设计时间估算方法难以满足日常生产需求这一现状,本文对产品设计时间预测方法进行了研究,创新性地将产品设计相似性应用于产品设计时间估算中,建立了基于产品设计相似系数的设计时间估算方法。
(2)已有的高斯过程元模型及嵌入知识的核近似等预测方法,虽然在某种程度上也能准确预测产品设计时间,但是这些方法往往复杂度较高,难以操作,更不易在企业推广实施。本文方法通过范例与已有算法进行对比,不仅说明了该方法的合理性和有效性,也反应出该方法客观性强、准确度高的特点,而且操作简单,易于在企业推广应用。
(3)在产品设计相似系数的过程中,所采用灰色关联分析法较为陈旧,而且所得关联度也随着分辨率的不同而变化,因此,今后研究方向可对此进行改进,以进一步提高设计时间预测的精确度。
[1]张昆仑,刘新亮.基于高斯过程元模型的产品设计时间估计方法[J].计算机集成制造系统,2011,17(1):18-22.Zhang K L,Liu X L.Time estimation method for product design based on Gaussian process meta-model[J].Computer Integrated Manufacturing Systems,2011,17(1):18-22.
[2]商志根,严洪森.基于概率支持向量回归的产品设计时间预测模型[J].计算机应用研究,2013,30(4):1099-1101,1104.Shang Z G,Yan H S.Forecast model for product design time basedon probabilisticsupport vector regression[J].Application Research of Computers,2013,30(4):1099-1101,1104.
[3]Cho S H,Eppinger S D.A simulation-based process model for managing complex design projects J.IEEE Trans on Engineering Management,2005,52(3):316-328.
[4]Zhang K L,Guo B.Application of metamodel approach in product development process [J].Journal of Computational Information Systems,2010,6(7):2159-2166.
[5]Yan H S,Wang B,Xu D,et al.Computing completion time and optimal scheduling of design activities in concurrent product development process[J].IEEE Trans on Systems,Man,and Cybernetics-Part A:Systems and Humans,2010,40(1):76-89.
[6]Xu D,Yan H S.An intelligent estimation method for product design time[J].International Journal of Advanced Manufacturing Technology,2006,30(7-8):601-613.
[7]YAN H S,XU D.An approach to estimating product design time based on fuzzy support vector machine[J].IEEE Trans on Neural Networks,2007,18(3):721-731.
[8]陈友玲,任晓杰.基于工序相似系数的工时计算方法[J].计算机集成制造系统,2014(4):866-872.Chen Y L,Ren X J.Method for determining time-quota based on similarity coefficient of process[J].Computer Integrated Manufacturing Systems,2014(4):866-872
[9]贡智兵.基于产品平台的快速设计关键技术研究及实现[D].南京:南京理工大学,2007.
[10]胡浩.基于三维CAD的产品快速设计系统的研究与应用[D].重庆:重庆大学,2010.
[11]郭波.面向产品开发过程仿真的知识工作基础数据研究[D].重庆:重庆大学,2007.
[12]谷梦瑶,陈友玲,杜萱萱.基于产品设计难度系数的设计时间估计方法[J].东北大学学报(自然科学版),2017,38(1):111-115.Gu M Y,Chen Y L,Du X X.Method for Determining Design Time Based on DifficultyCoefficient of Product Design[J].Journal of Northeastern University(Natural Science),2017,38(1):111-115.
[13]商志根,严洪森.基于核近似的产品设计时间预测[J].计算机集成制造系统,2011(6):1144-1148.Shang Z G,Yan H S.Product design time forecast based on kernel approximation[J].Computer Integrated Manufacturing Systems,2011(6):1144-1148.
[14]Jin J L,Wei Y M,Zou L L,Liu L,FuJ.Risk evaluation of China’s natural disaster systems:an approach based on triangular fuzzy numbers and stochastic simulation[J].Natural Hazards,2012,621:554-559.
[15]朱凌云.面向大规模定制产品设计的客户需求处理关键技术研究[D].合肥:合肥工业大学,2008.
[16]Li X M,Hipel K W,Dang Y G.An improved grey relational analysis approach for panel data clustering[J].Expert Systems with Applications,2015,42(23),9105-9116.
[17]Wang X G,QiuHB,SuJ,etal.Research of Test Method for the Bogie Rotary Torque[J].Advanced Materials Research,2012,1766(503):1045-1049.
