化斜移为平移
2018-05-27傅昌平
傅昌平

近年来,全国各地中考数学试卷中频频出现抛物线上平行四边形的判定问题,这类问题是典型的二次函数与几何的结合题。一方面这种综合题型牵涉的知识面很广,全等三角形、四边形的性质和判定、一元二次方程、二次函数、相似三角形等初中重要的知识点都悉数包括;另一方面这种题型也集中体现了中学数学中的分类讨论、转化化归、函数方程,数形结合等重要的思想。它注重考查学生对知识的融会贯通,迁移应用及延伸拓展,它要求学生要具备很强的分析问题、探究问题和逻辑推理等能力,所以往往在中考数学试卷中都是以压轴题的形式出现。处理这类题型需要掌握一定的处理技巧,这就是“化斜为直”,也就是将问题中的斜线段平行且相等转化为竖直线段和水平线段相等,即“化斜移为平移”。下面结合具体试题就这一问题作简要探讨.
例1 (2015年德州中考试题)已知抛物线y= -mx2+4x+2m与x轴交于点A(α,0),B(β,0),且■+■=-2.
(1)求抛物线的解析式.
(2)抛物线的对称轴为L,与y轴的交点为C,顶点为D,点C关于L的对称点为E.若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.
简解:(1)易求y=-x2+4x+2.;
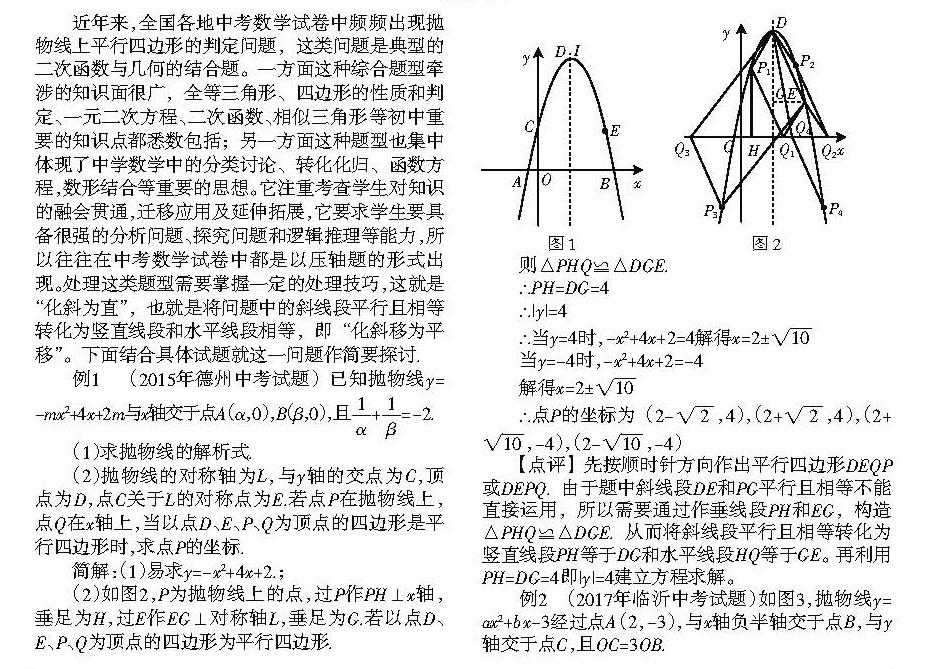
(2)如图2,P为抛物线上的点,过P作PH⊥x轴,垂足为H,过E作EG⊥对称轴L,垂足为G.若以点D、E、P、Q为顶点的四边形为平行四边形.
■
则△PHQ≌△DGE.
∴PH=DG=4
∴|y|=4
∴当y=4时,-x2+4x+2=4解得x=2±■
当y=-4时,-x2+4x+2=-4
解得x=2±■
∴点P的坐标为(2-■,4),(2+■,4),(2+■,-4),(2-■,-4)
【点评】先按顺时针方向作出平行四边形DEQP或DEPQ.由于题中斜线段DE和PG平行且相等不能直接运用,所以需要通过作垂线段PH和EG,构造△PHQ≌△DGE.从而将斜线段平行且相等转化为竖直线段PH等于DG和水平线段HQ等于GE。再利用PH=DG=4即|y|=4建立方程求解。
例2 (2017年临沂中考试题)如图3,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
■
(1)求抛物线的解析式;
(2)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由。
简解:(1)易求抛物线的解析式为y=x2-2x-3;
(2)存在,如图4,当AB为对角线时,易得平行四边形AM1BN1,∴M1(0,-3).
当AB为一边时,在平行四边形ABM2N2中,点A的横坐标是2,点N2的横坐标是1,点B的横坐标是 -1,由图形平移前后点的坐标关系,得点M2的横坐标是-2,纵坐标(-2)2-2×(-2)-3=5.
∴M2(-2,5).
在平行四边形ABN3M3中,点B的横坐标是-1,点N3的横坐标是1,点A的横坐标是2,由图形平移前后点的坐标关系,得点M3的横坐标为4,∴点M3的纵坐标为42-2×4-3=5,
∴M3(4,5)。
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(-2,5)或(0,-3).
【点评】题中A、B两点是抛物线上两定点,M、N分别是抛物线及其对称轴上两点,根据线段AB所在的位置,当以AB为对角线作平行四边形时,利用对角线互相平分的四边形是平行四边形,很容易找到M(0,-3);当以AB一边作平行四边形时,利用一组对边平行四边形,按顺时针作出平行四边形ABMN和平行四边形ABNM,从而找到M2、M3,再将条件中的AB平行且等于MN,由图形平移前后点的坐标关系,将这一“斜移转化为平移”.具体做法是:
A(2,______)→N(1,_____)得B(-1,_____)→M(-2,_____)
或B(-1,_____)→N(1,____)得A(2,_____)→M(4,_____)
再将M点的横坐标代入抛物线的解析式中,求出纵坐标。上述两题的方法可以通用,同学们不妨试试。
至于其他类型的特殊平行四边形,可以先根据条件判定它的形状,然后再通过上述方式转换。例如:
例3 (2017年兰州中考试题)如图5,抛物线y= -x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-■x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
■
(1)求抛物线y=-x2+bx+c的表达式;
(2)在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
简解:(1)易求抛物线的解析式为y=-x2-2x+4;
(2)如图4,易知直线AB的解析式为y=2x+4,设E(a,2a+4)则Fa,-■a-6.
过点A作AQ⊥EF于Q过H作HP⊥EF于P,
∵直线AB的解析式为y=2x+4,直线AC的解析式为y=-■x-6,
∴AB⊥AC.当四边形AEHF是平行四边形时,四边形AEHF是矩形.
∵EH∥AF,EH=AF.∴∠HEP=∠AFQ.
又∵∠EPH=∠FPA=90°,∴△EPH≌△FQA.∴PH=AQ,EP=FQ.
∴0-a=a-(-4),解得a=-2.∴E(-2,0)
0-yH=-4--■a-6解得yH=-1.∴H(0,-1).
【點评】第(2)题易证∠BAC=90°,故当四边形AEHF为平行四边形时,四边形AEHF是矩形,通过作垂线段HP、AQ,利用EH与AF平行且相等构造△EPH≌△FQA,从而化斜线段EH=AF为竖直线的EP=QF,水平线段PH=AQ,建立等式求解。
总之,这类题型解法的第一步是根据特殊四边形的判定作出相应的图形,然后再将题中的一组对边平行相等这一关键条件进行相应的“化斜为直”的转换。初中阶段数学课本上介绍的平移是水平方向或竖直方向,而特殊四边形一组对边平行且相等可以看作任意方向上的平移。这就需要我们在解题过程中利用转化、化归思想化“未知为已知”,通过构造三角形全等或利用平移过程中的横或纵坐标的变化规律将任意方向上的平移转化为水平方向或竖直方向的平移,从而使问题迎刃而解。因此,在平时的学习过程中,需要加强这种数学思想方法的训练,才能探究新知,完成对知识能动的正向迁移。
(作者单位:安徽省南陵县春谷中学)
