同底数的指数函数和对数函数图像位置关系探究

☉湖北省武汉市武汉中学 刘志江

三个函数y=ax、y=x和y=logax有哪些位置关系？当a＞1时，函数y=ax的图像恒在直线y=x的上方吗？答案是否定的.事实上，对于y=2x，y=3x的图像来说，它们在直线y=x的上方，但是，像y=1.2x，当x=2时，y=1.22=1.44＜2，即可知f（x）=1.2x不是恒在直线y=x的上方.下面我们利用对函数y=ax、y=logax与y=x的图像之间的位置关系进行探讨.

一、函数y=ax与y=x的图像的位置关系

令f（x）=ax-x，则f′（x）=axln a-1.

当0＜a＜1时，f′（x）=axln a-1＜0，函数f（x）=ax-x在（-∞，+∞）上是单调减函数，因为f（0）=a0-0=1＞0，f（1）=a-1＜0，所以f（0）f（1）＜0，故在区间（0，1）上有且仅有一个零点，即函数y=ax与函数y=x在区间（0，1）有且仅有一个交点.当a＞1时，若f′（x）=axln a-1=0，则x=-loga（ln a）存在，此时f（-loga（ln a））=a-loga（lna）+loga（ln a）=logae+loga（ln a）=loga（eln a）.

当a＞1时，列表如下：

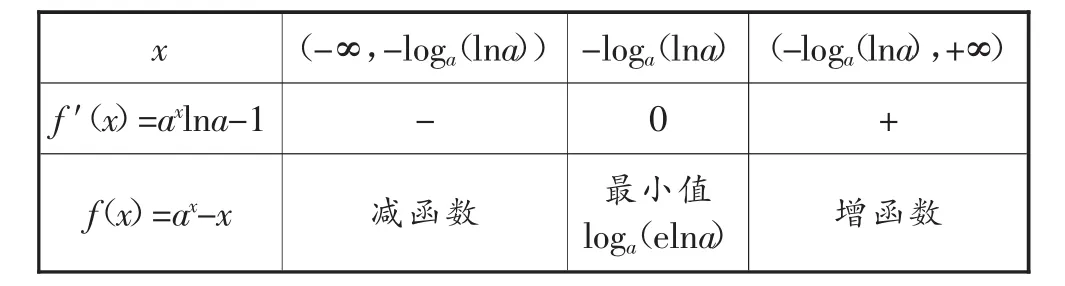
x（-∞，-log a（ln a））-log a（ln a）（-log a（ln a），+∞）f′（x）=ax ln a-1-0+f（x）=ax-x减函数最小值log a（eln a）增函数

若最小值log（aeln a）＞0，即eln a＞1，得这就是说时，函数（fx）=ax-x没有零点，即y=ax与y=x相离；

若最大值log（aeln a）=0，即eln a=1，得，这就是说当时，函数（fx）=ax-x只有一个零点，即y=ax与y=x相切，此时x=-log（aln a）=e，即切点为点（e，e）；

若最大值log（aeln a）＜0，即eln a＜1，得这就是说当时，函数（fx）=ax-x有两个零点，即y=ax与y=x相交.

二、函数y=log ax与y=x图像的位置关系

令g（x）=logax-x，其中x∈（0，+∞）.

因为g（′x），所以讨论如下：

1.当0＜a＜1时，＜0，函数g（x）=logx-x在a（0，+∞）上是单调减函数，由于g1-a＞0，所以g，故在区间）上有且仅有一个零点，即函数y=logax与y=x在区间有且仅有一个交点.

2.当a＞1时，则x=log e＞0存在，a

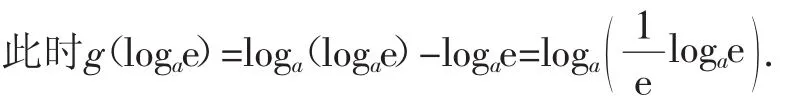
当a＞1时，列表如下：

x （0，log a e） log a e （log a e，+∞）g′（x）=log a e x-1 + 0 -g（x）=log ax-x 增函数最大值log a（ ）1 e log a e 减函数

（1）若最大值这就是说当时，函数g（x）=logax-x没有零点，即函数y=logax与y=x的图像相离；

（2）若最大值这就是说当时，函数g（x）=logax-x有一个零点，即函数y=logax与y=x的图像相切，此时x=logae=e，切点为点（e，e）；

（3）若最大值，这就是说当时，函数g（x）=logax-x有两个零点，即函数y=logax与y=x的图像相交.

三、函数y=ax与y=log ax的图像之间的位置关系

由于函数y=ax与y=logax互为反函数，所以由以上的讨论可知：

2.当时，函数y=ax与y=logax的图像都和直线y=x相切于点（e，e）.

3.当，由以上讨论可知，函数y=ax与y=logax的图像有两个交点，并且这两个交点都在直线y=x上.

4.当0＜a＜1时，函数y=ax与y=logax的图像之间有怎样的位置关系？它们有且仅有一个交点吗？为此，我们构造函数如下：

令h（x）=ax-logax，其中x∈（0，+∞）.

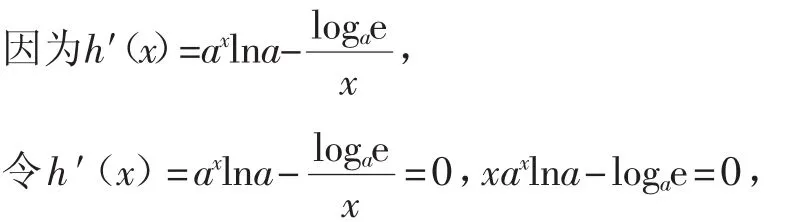
即xax-（logae）2=0.

为了判断上式根的个数，即判断出方程logax+x=loga（logae）2根的个数，为此再次构造函数k（x）=logax+x-

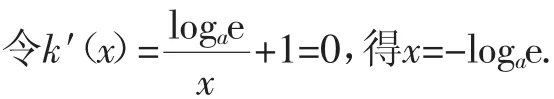
当0＜a＜1时，列表如下：

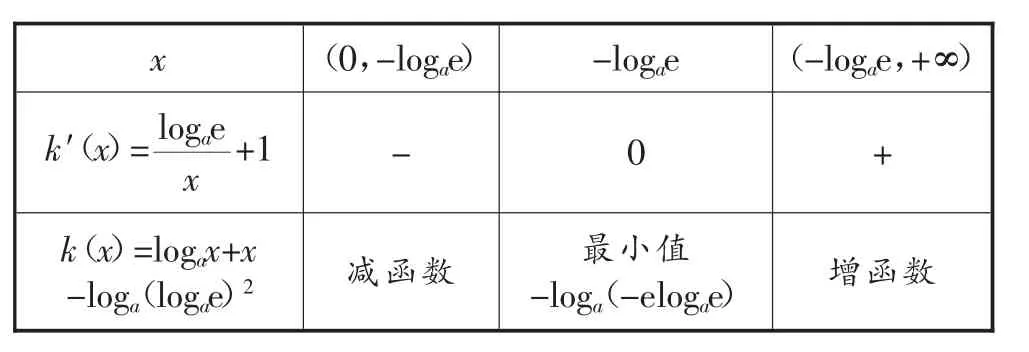
x （0，-log a e） -log a e （-log a e，+∞）k′（x）=log a e x +1 - 0 +k（x）=log ax+x-log a（log a e）2减函数最小值-log a（-elog a e）增函数

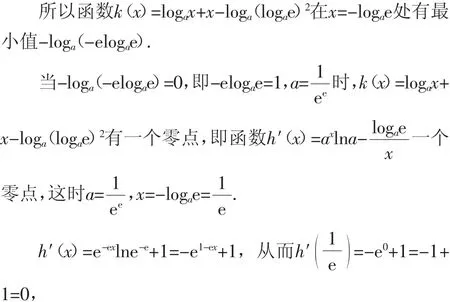
所以h（x）=ax-logax在x∈（0，+∞）上是增函数.

因为h（a）=aa-logaa=aa-1=aa-a0＜0，h（1）=a-loga1=a＞0，所以h（a）h（1）＜0.

因此，时，函数h（x）=ax-logx在x∈（0，+∞）a上有且仅有一个零点，即函数y=ax与函数y=logax在区间（a，1）内有一个交点.

5.下面讨论当0＜时y=ax与函数y=logx交点情况：a

函数k（x）=logax+x-log（alogae）2与x轴有两个交点，设两个交点分别为A（x1，0）与B（x2，0），0＜x1＜-logae＜x2，所以h（x）=ax-logax在x∈（0，x1）和x∈（x2，+∞）上是增函数，在（x1，x2）上是减函数，所以在x=x1处，函数h（x）=ax-logax有极大值，在x=x2处，函数h（x）=ax-logax有极小值.

由于x→0，h（x）=ax-logax＜0，x→+∞，h（x）=ax-logax→+∞；

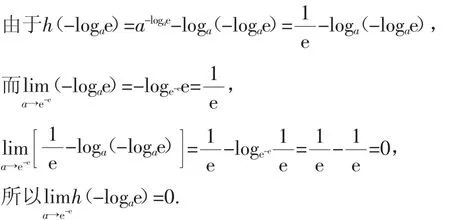
由于函数h（x）在（x1，x2）上是减函数，

所以h（x1）＞h（-logae）＞h（x2），

即h（x1）＞0＞h（x2），因此函数y=h（x）在x∈（0，x1）和x∈（x2，+∞）上各有一个零点，在区间（x1，x2）也有一个零点，从而得到：

当时，在区间（0，x），区间（x，x）和（x，+∞）1122上各有一个交点，这就是说函数y=ax与函数y=logax在区间（0，x1），区间（x1，x2）和（x2，+∞）各有一个交点，其中在区间（x1，x2）内它们的交点在直线y=x上，因此0＜函数y=ax与函数y=logax有三个不同的交点.

综上所述，我们有如下结论：

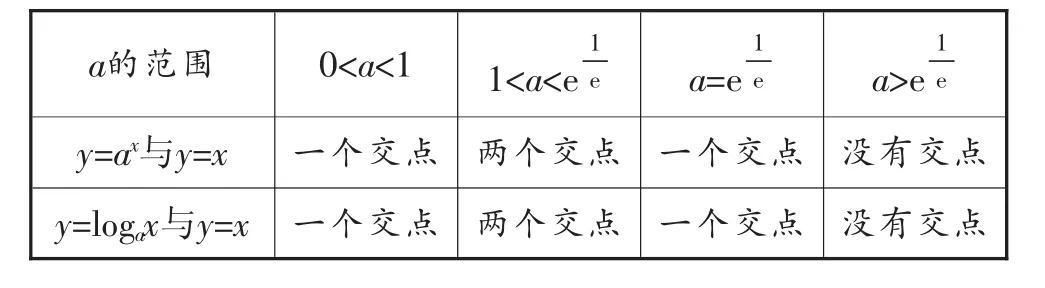
a的范围 0＜a＜1 111 1＜a＜e e a=e e a＞e e y=ax与y=x 一个交点 两个交点 一个交点 没有交点y=log ax与y=x 一个交点 两个交点 一个交点 没有交点

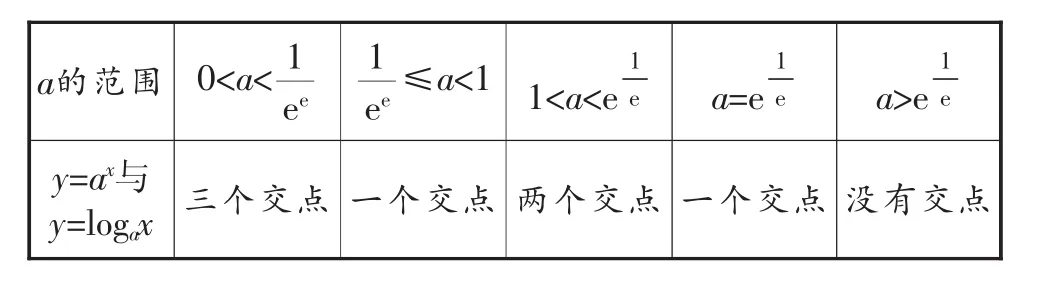
a的范围 0＜a＜ 1 e 1 1 1 e 1 ee≤a＜1 1＜a＜e e a=e e a＞e e y=ax与y=log ax 三个交点 一个交点 两个交点 一个交点 没有交点

1.钱佩玲，邵光华.数学思想方法与中学数学.北京师范大学出版社，2000（3）.

2.宗敏，对数函数与指数函数的图像的交点个数的再探讨.考试周刊，2010（3）.H