一道解三角形测试题的命制与反思

☉四川省攀枝花市第三高级中学校 冯蓉波

2017年9月，我接到参加攀枝花市高三第一次统考数学试题命制工作的通知.笔者多次参加这种试题的命制工作，但以往主要任务是压轴题.四川省从2017年起使用全国卷Ⅲ，风格发生了不小的变化.四川卷难易差距大，基本题简单，压轴题难；而全国卷不管大题小题中档题居多，每题都有较大的思维容量.处在全国卷第17题的三角函数近几年均考查与三角形相关问题，难度中等.对已经习惯多年第17题轻松得分的学生和老师来说这一题还有点不适应，加之从2017年开始，全国卷取消了选考题中的几何证明选讲，这意味着平面几何的知识和方法将在其他题中体现.三角形正好是平面几何知识与方法的良好载体，数形结合思想能得以充分体现，解三角形的试题在高考大题中的地位更加牢固.

一、灵感

三角形的五个“心”是三角形重要的几何特征，湖南师大沈文选教授曾以三角形的五个“心”为载体，将竞赛中的平面几何问题作了归类，使学生对平面几何的学习更有条理.“重心”是高中生最熟悉的，它是三角形三边中线的交点，一定在三角形内；“内心”是三角形内切圆的圆心，也是三角形内角平分线的交点，一定在三角形内.若能将三角形的重心与内心结合，图形将丰富而生动，同时学生也不会感到陌生.

二、寻根

（一）三角形内角平分线相关结论

《人教版八年级上册数学》第56页拓广探索12题［1］：

如图1，在△ABC中，AD是它的角平分线. 求证：S△ABD∶S△ACD=AB∶AC.

（二）三角形中线长公式

《普通高中课程标准实验教科书数学人教A版必修5》P20习题1.2A组13题［2］：△ABC三边分别为a，b，c，边BC，CA，AB上的中线分别记为ma，mb，mc，应用余弦定理证明：ma=

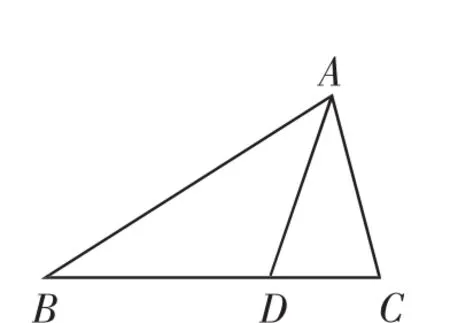
图1

（三）2017年高考数学考试大纲

解三角形：（1）正弦定理、余弦定理：掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.（2）应用：能够运用正弦定理、余弦定理等知识和方法解决一些与测量与几何计算有关的实际问题［3］.

根据大纲要求，正弦定理、余弦定理的直接运用就是解三角形，即根据三角形三个独立条件（已知三个角除外），求出三角形的其他元素，基本方法是用正弦定理、余弦定理（常常离不开三角形的内角和定理、面积公式等知识）［4］；基本方法就是边角转化，三个独立条件往往不是直接给定，其中有的通过角的关系（三角方程）、边的关系或边角关系来给定，这时也考查了三角恒等变形的知识与方法.

（四）全国卷高考试题

（2015年全国卷Ⅱ第17题）在△ABC中，D是BC上的点，AD平分∠BAC，△ABD面积是△ADC面积的2倍.

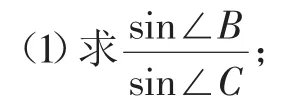
（2）若AD=1，求BD和AC的长.

运用课本基本知识与方法来编拟市统考题能追根溯源，运用高考原题的思路，既能体现这一章节的高考方向，又能考查这一部分基本方法与数学思想.

三、命制

（一）确定图形

根据三角形全等的判定定理：SSS，SAS，ASA，AAS可确定唯一的三角形，而SSA（边边角）可能无解，或一解，或两解（人教A版必修5P8-P9探究与发现有详细讨论）［2］.即根据三角形三个独立条件（三个角除外），可以让三角形定下来.由于是高三第一次统考，不能让问题过于复杂，先确定一个等腰三角形：如图2，a=c=2b=4，然后由点A出发作出中线与内角平分线.

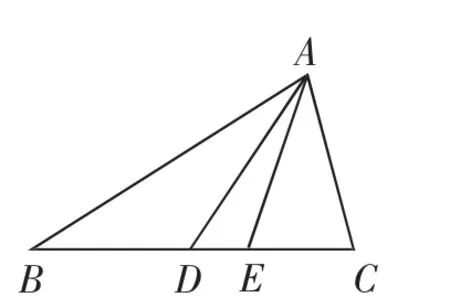
图2

（二）设问

在图2中，最引入注目的应是△ADE，从△ABC中不能得到任何一个直接的边或角，所以一定要在△ADE上产生问题，第一感觉是“第（2）问：求△ADE的面积”.

第（1）问是求△ADE的边长好还是求△ADE的内角的三角函数值呢？求△ADE的内角的三角函数值似乎这三条边都要求，或利用差角或外角或补角来求，问题变得复杂.所以还是求△ADE某一边或线段BE或CE的长好些.若求线段DE、BE或CE的长，第（2）问若求△ADE的面积可直接通过等高的三角形面积比等于底之比来求，变得很单薄.若求AE的长，学生可能会通过半角公式求出∠EAC的正弦或余弦，在△ACE中用正弦定理来解.而求AD的长直接与课本习题接轨简单明了.于是决定将第（1）问设定为求线段AD的长.

第（2）问是求△ADE的面积还是求△ADE内切圆半径（面积）或外接圆半径（面积），求△ADE内切圆半径（面积）不仅要求出△ADE的面积，还要求出△ADE的周，其中L为三角形的周长 ）；若求外接圆半径（面积），则由正弦定理须求出某内角的正弦及对边，主要是求角比较复杂.于是第（2）问设定为求△ADE的面积.

（三）推敲

△ABC的三个独立条件用SSS给出会使问题显得过于平淡，不便于考查三角恒等变换以及正余弦定理的应用.参考2017年全国卷Ⅲ第17题：△ABC的内角A，B，C的对边分别为a，b，c，已知sin

（1）求c；

（2）设D为BC边上一点，且AD⊥AC，求△ABD的面积.

△ABC的三个独立条件用了边边角给出，只需用同角关系求出A角的正切值即可求出角A，比较轻松.模仿2017年全国卷Ⅲ，将“a=4”抹去，直接给出从方程的观点来看这两个方程在此三角形中是等价的，可以确定同一个三角形.

第1稿：如图3，△ABC的内角A，B，C的对边分别为a，b，c，D，E为线段BC上的点，AD，AE分别过△ABC的重心

与内心.已知c=2b=4，tan

（1）求线段AD的长；

（2）求△ADE的面积.

1.推敲1

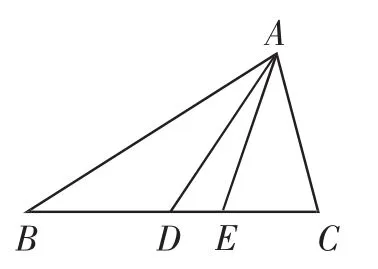
图3

已知条件中强调了△ABC的重心与内心，概念性太强.如果学生不知道这两个概念，此题将无法入手而得零分，这不是命题人的本意，所以要改变两个条件的叙述.

第2稿：将第1稿中“AD，AE分别过△ABC的重心与内心”直接叙述为“BD=CD，∠BAE=∠CAE”.

2.推敲2

对比2017年全国卷Ⅲ第17题的难度，第（1）问相当，但全国卷Ⅲ的第（2）问变化多，如果不用面积比来实现求△ABD的面积，则须解△ABD，△ACD，但这两个三角形都差一个条件，需建立方程来求解就难了.于该题的第（2）问变化并不多，可直接求底和高，常用思路并不困难，于是对tan的条件进行改变.变为“2c cos C=b”.

3.推敲3

方程2c cos C=b中如果学生发现b，c边的关系，可直接求出cos，比第2稿更简洁.但这里考查了学生

第3稿：将第1稿中的的观察能力，能观察得到这一结论获得这一结果是对这类学生的奖偿.若不能观察出，则可用正弦定理进行边化角，可得sin2C=sin B，因为b＜c，所以B＜C，所以B＜2C.

因为B，2C∈（0，2π），所以B+2C=π.

因为A+B+C=π，所以A=C.

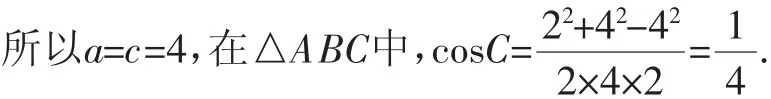
也可用余弦定理化为（c2+acb2>）=0.

而c2+ac-b2=12+4a＞0，所以a=c.所以a=c=4，

在△ABC中，也可得出cos

第4稿：将第3稿中的方程“2c cos C=b”变成与两个角相关的等价条件“sin2C=sin B”.

4.推敲4

将方程“2c cos C=b”变成等价条件“sin2C=sin B”.学生由正弦定理变成“2c cos C=b”，进而得到cos得非常巧妙！这条路不明朗，可能性小.而用第3稿的方法直接用函数值相等得到角的方程可能性大.

这两个条件的取舍上中心组成员也产生了很大的争执，关键是直接给出两边是正弦值相等，方向诱导性很强，没有边角均有的“2c cos C=b”丰富.也设法变换成但小题中也出现诱导公式，这种变换也只增加了诱导公式的考查，没有太大改变.权衡之下，最终还是选择了第3稿.

（四）定稿

如图4，△ABC的内角A，B，C的对边分别为a，b，c，已知c=2b=4，2c cos C=b，D，E为线段BC上的点，且BD=CD，∠BAE=∠CAE.

（1）求线段AD的长；

（2）求△ADE的面积.

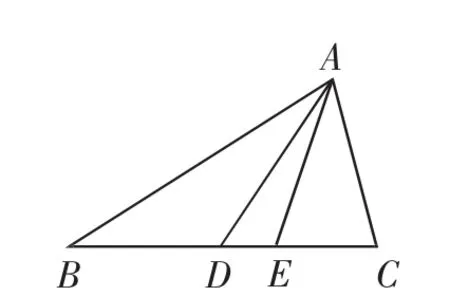
图4

四、解答

（一）第（1）问分两步

第1步：求a.

方法1：因为2c cos C=b

由余弦定理知，c2=a2+b2-2ab cos C⇒42=a2+22-2×2×a×

方法3：因为2c cos C=b，所以(c2+ac-b2=12+4a＞0，所以a=c.所以a=c=4.

第2步：求AD的长.

方法1（用中线长公式）：由a=4，得BD=2.

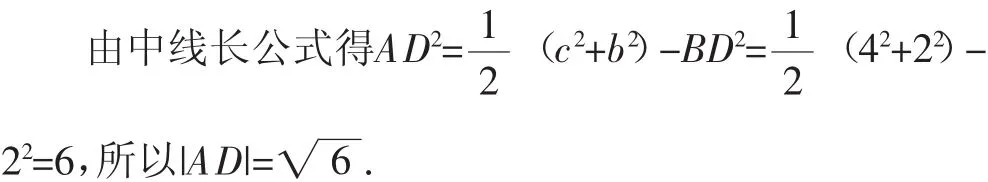
方法2（用余弦定理）：由a=4，得CD=2.

方法2：因为2c cos C=b，由正弦定理得sin2C=sin B.

因为b＜c，所以B＜C，所以B＜2C.

因为B，2C∈（0，2π），所以B+2C=π.

因为A+B+C=π，所以A=C.

所以a=c=4.

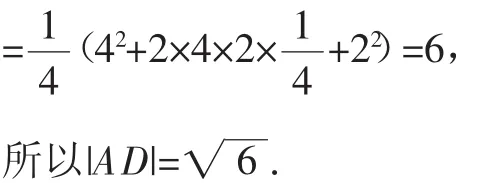
（二）第（2）问分两步

第1步：求DE的长.

方法1（用正弦型面积公式）：因为

所以EC

方法2（用三角形内角平分线定理）：如图5，过点E分别作AC，AB的垂线，垂足分别为F，G.

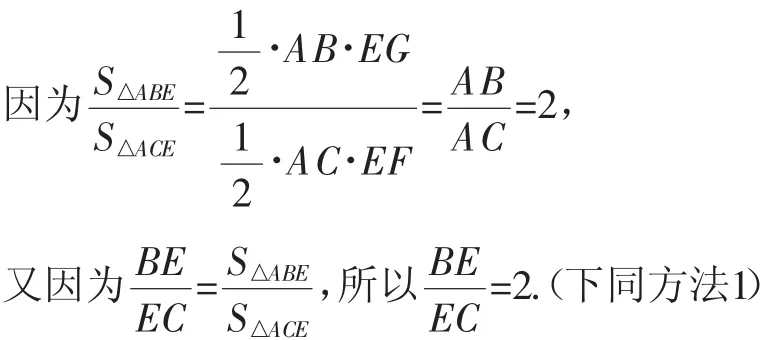
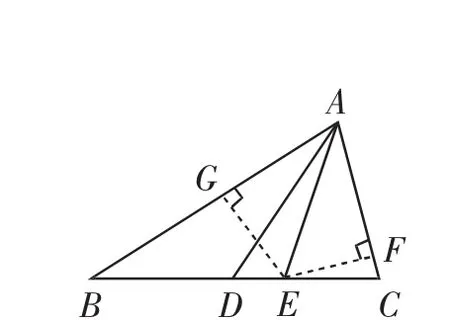
图5

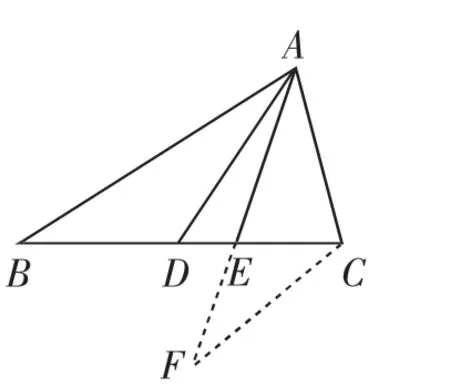
图6

方法3（用相似形）：如图6，过点C作AB的平行线交AE的延长线于F，则∠BAE=∠F，所以∠EAC=∠F，所以CF=AC.

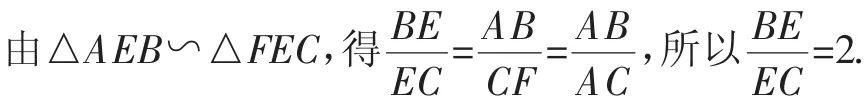
（下同方法1）

第2步：求△ADE的面积.

方法1（直接求高）：因为2c cos C=b，所以所以△ADE中，DE边上的高为h=

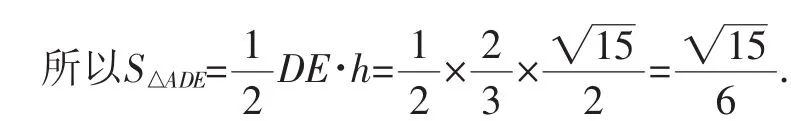
方法2（用等高的三角形面积比等于底之比）：因为2c cos C=b，所以cos

五、反思

（一）对两道高考题与本题所用方法归类

2017年全国卷Ⅲ第17题、2015年全国卷Ⅱ第17题以及本题的第（2）问都运用了同一方法：“等高的三角形的面积比等于底之比.”若推广为含三角形式的结论为：

如图7，在△ABC中，∠BAD=θ，∠CAD=φ.

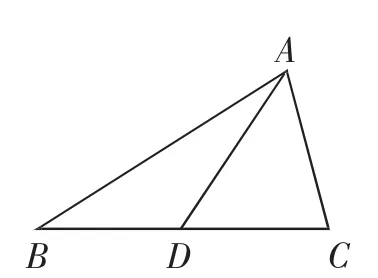
图7

在2015年全国卷Ⅱ第17题以及本题中，θ=φ，所以

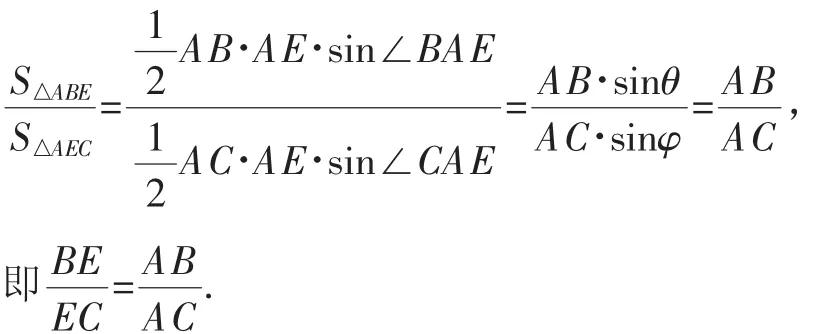
在2017年全国卷Ⅲ第17题中，θ=90°，φ=30°，

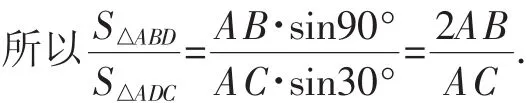
运用这个结论，所命制的统考题（定稿）还可以通过∠CAE来求∠DAE.

（二）对本题特点分析

本题紧扣教材与考纲，既考查学生的平面几何的基本知识与方法，又考查了正弦定理余弦定理的应用与三角恒等变换的知识与方法，将三角形的面积比、边长比、角的正弦值之比有机结合.难度适中，思维角度广，解题方法多，也便于老师在考后运用本题对解三角形问题进行分析与归纳.

（三）对本题考试结果的反馈

本题全市理科平均分为6.2分，作为大题第一题，分数偏低.第（1）问大多数学生还能根据已知条件应用正余弦定理对△ABC和△ABD求解；在第（2）问很多学生试图去求△ADE的内角来求面积而失败，未能通过与△ABC的面积比来转化.这是学生惯性，学生在题海中固化了这一方法.这说明了高三教师对近几年高考题考查的方法与思路研究不够，不能从提高学生关键能力的角度展开教学，还在题海之中.在第一次全市教研会上我引用了本题作了关于三角函数的微专题复习的发言.

（四）对试题命制的反思

作为命题小组成员，十多年来从模仿到改编，从改编到原创，历经磨难，对自己总是难以满意.究其原因：一是理论水平不高，二是素材积累不够.因此，平时应反复理解数学核心素养的本质，多阅读与试题命制相关的理论文章，也多学习同行的命题过程与心得，欣赏命题的内在本质与美，提升自身素养.多挖掘核心概念，对教材中的例题、习题等内容进行改编与整合，在课堂上学生提出的新的观点、方法收集整理，在教研会上教师之间多交流碰撞，对高考试题钻研、归类，对竞赛试题与高校自主招生试题多作研究，总会找到新的素材与方法，命制出满意的试题.

1.人民教育出版社课程教材研究所中学数学课程教材研究开发中心.义务教育教科书八年级上册数学［M］.北京：人民教育出版社，2013.

2.人民教育出版社课程教材研究所中学数学课程教材研究开发中心.普通高中课程标准实验教科书数学必修5［M］.北京：人民教育出版社，2007.

3.教育部考试中心.2017年普通高等学校招生全国统一考试大纲理科［M］.北京：高等教育出版社，2016.

4.罗增儒.一道2017年高考三角试题的双面剖析［J］.中学数学教学参考（上旬），2017（10）.H