高烈度区长联大跨连续梁减隔震设计研究

刘洋，赵人达，向星赟，王超，高能

近几十年来，减隔震技术作为提升结构抗震性能的一种技术得到了广泛发展和应用。减隔震技术通过采用减隔震装置将结构或构件与可能引起破坏的地震地面运动或支座运动分离开来，大大减少传递到下部结构的地震力和能量[1-2]。减隔震的基本原理为：利用柔性支撑以延长结构的自振周期，从而减小结构在地震作用下的响应；利用阻尼器或耗能装置以控制由于周期延长而导致的过大相对位移。同时减隔震装置应具有足够的刚度和强度，以支撑正常使用极限状态下的水平力[3]。位于高烈度区的长联多跨连续梁按照传统的抗震设计方法，一般只设置1个制动墩。地震作用下纵桥向的地震荷载基本由制动墩承受，因此制动墩及其下部结构处于不利的受力状态[4]，支座作为上、下部的连接构件也很难满足抗震设计规范要求，制动墩及其基础的设计也会一定程度上增加资金投入。与传统抗震设计相比，减隔震设计能从根本上减小结构的地震响应，能同时达到既经济又较容易满足现行桥梁抗震设计规范要求的效果。在高烈度区，减隔震设计可以采用高阻尼橡胶支座、双曲面球型隔震支座、液体黏滞阻尼器等减隔震装置。本文结合某大跨度预应力连续梁，分析采用液体黏滞阻尼器、双曲面球型隔震支座2种常用的减隔震设计方案的减隔震效果。

1 工程概况及有限元模型

1.1 工程概况

高烈度区某预应力混凝土连续梁跨径布置为(55+4×90+55) m，其总体布置如图1所示：

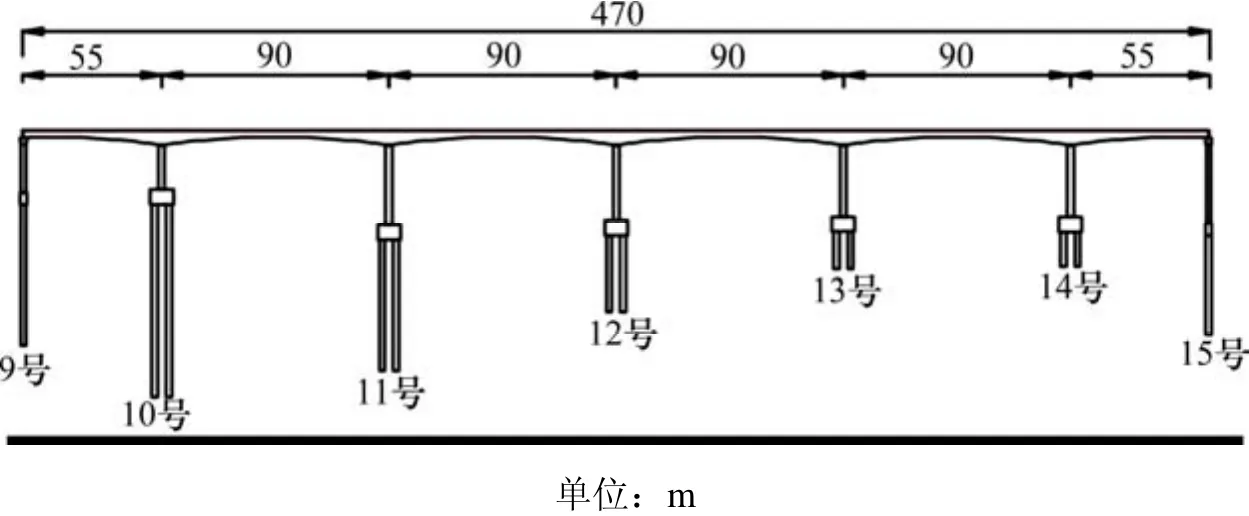
图1 桥梁总体布置图Fig. 1 Engineering drawing of the bridge

主梁上部结构为变截面连续箱梁，单幅桥面宽12.5 m，支点梁高5.6 m，跨中梁高2.6 m联间主墩为 2.5 m(顺桥向)×6.5 m(横桥向)×0.6 m(壁厚)薄壁箱形截面，顺桥向的截面惯性矩为8.718 m4，联间过渡墩为实心矩形截面,顺桥向的截面惯性矩为：1.367 m4。梁体质量为16 533 t，9～15号墩的墩高分别为：18.9，17.2，31.1，29.8，27.9，28.0和31.1 m，其中 11号墩为制动墩。桥址场地安全评估报告提供50 a 2.5%(2 000年一遇)的地震动峰值加速度为0.283 g。非隔震时结构(采用盆式支座)的第1阶自振周期为6.78 s，体现为制动墩顺桥向的弯曲振动。本文基于以下3种设计方案进行分析比较：

1) 传统抗震设计方案：墩梁间采用盆式支座，其中11号墩设置固定支座，其余各墩为活动支座；

2) 液体黏滞阻尼器隔震设计方案：在方案 1)的基础上，在除边墩外的非制动墩上各增设1个液体黏滞阻尼器，通过调整阻尼参数来改善结构地震响应[5]。

3) 双曲面球型隔震支座设计方案：在每个墩顶各设置2个双曲面球型隔震支座，并在11号墩的双曲面球型隔震支座上设置剪力键[6-7](抗剪螺栓)在强震作用下，剪力键失效，实现大跨连续梁结构在地震作用中的体系转换。

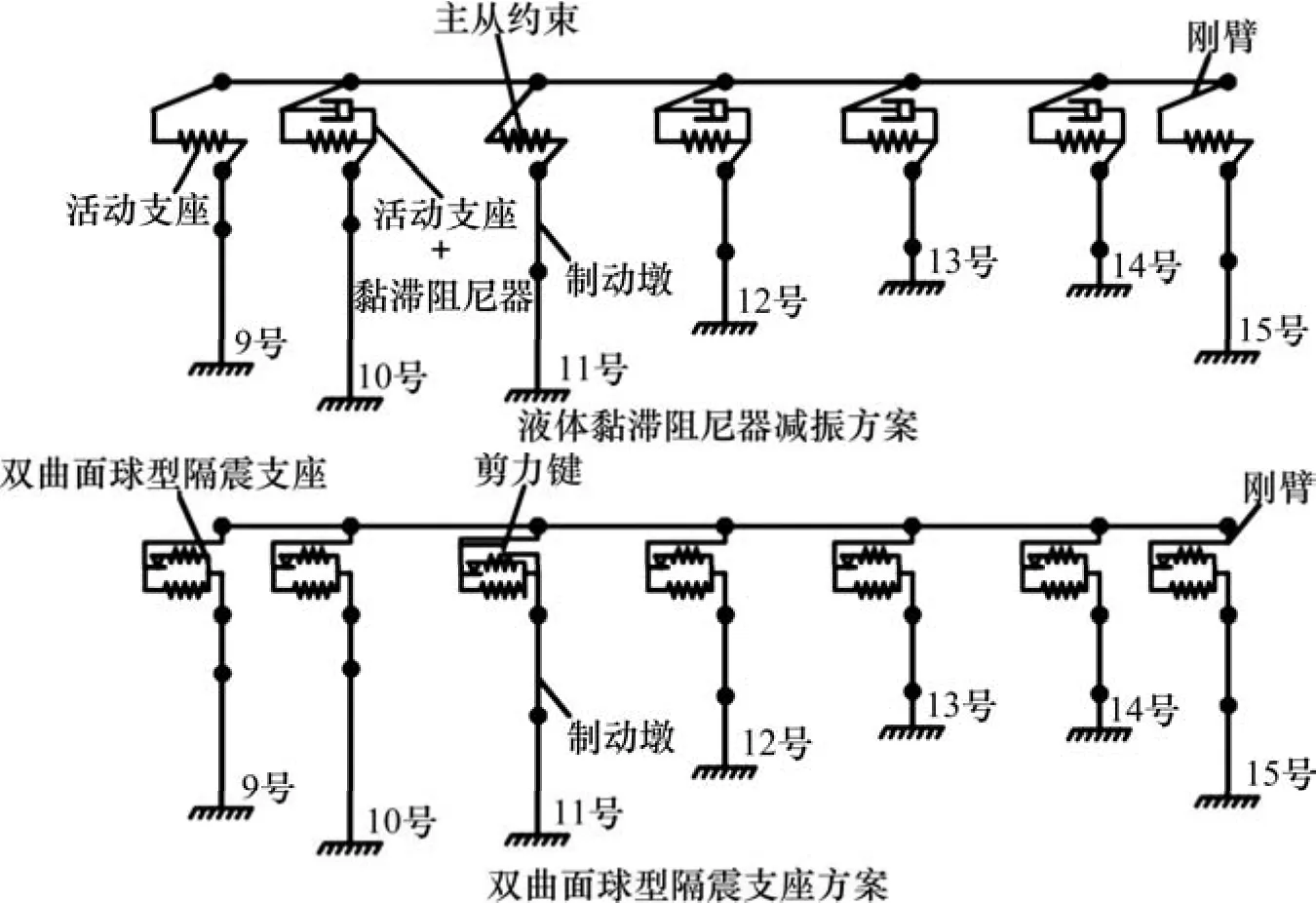
图2 有限元计算模型示意图Fig. 2 Finite element model for the calculation

1.2 有限元模型

本文运用空间分析软件ANSYS建立精细有限元模型对桥梁模型进行了地震作用下的时程响应分析，有限元模型中主梁、墩柱均采用 BEAM188三维弹性梁单元，可以同时考虑拉压、扭转、弯曲及剪切变形的影响，主梁通过竖向刚臂连接支座；桩基周围土的约束作用，可用土弹簧进行模拟，土弹簧可采用 COMBIN14模拟，弹簧刚度数值可采用“m法”确定[8]，土的抗力取值比静力大一般取m动=(2～3)m静。固定支座采用主从约束模拟。

液体黏滞阻尼器的阻尼力与运动速度间的关系为：

式中：F为阻尼力；C为阻尼器的阻尼系数；V为阻尼器两端的相对速度；α为阻尼指数，常用值在0.3～1.0 之间[9]。

根据式(1)的特点，液体黏滞阻尼器可采用非线性弹簧单元COMBIN37模拟。COMBIN37单元为非线性一维单元，由2个活动节点(i，j)和可选的2个控制节点(K，L)组成，Combin37能通过下列公式展现其非线性功能：

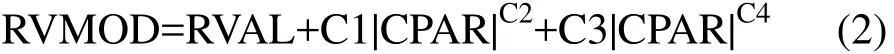
式中：RVAL 为实常数值。可表示弹簧力、阻尼系数等，本文中令Keyopt(6)=2则实常数值代表阻尼系数。

CPAR为控制变量。可表示位移、位移对时间的1阶导数等，本文中令Keyopt(1)=2时，则控制变量为位移对时间的一阶导数即为速度v。

C1，C2，C3和C4为实常数值。通过实常数设定命令r设定，可取任意值；RVMOD是RVAL的修正值。

参数设置如下：在式(2)中令RVAL=0，C3=C4=0，CPAR=v，则 RVMOD=C=C1|v|C2，则

对比(1)，(3)知C1代表阻尼系数C，C2+1代表阻尼指数α，所以可得C1=C，C2=α-1。

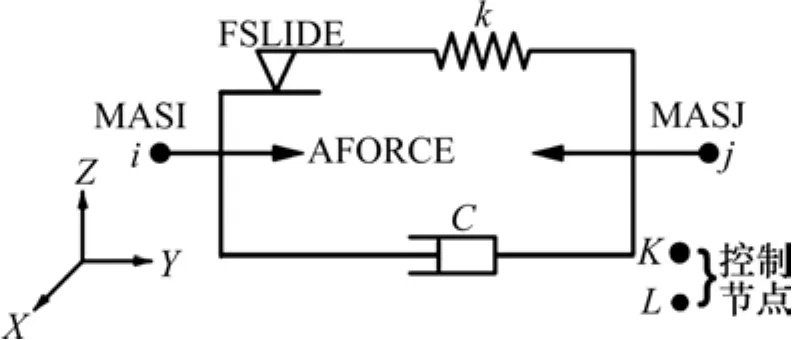
图3 COMBIN37力学模型Fig. 3 Mechanical model of COMBIN37

双曲面型球型支座可以用等效线性模型模拟[10]，其滞回曲线如图4所示：

图4 双线性滞回模型Fig. 4 Bilinear hysteretic model

根据其力学特性，双曲面球型隔震支座可采用非线性弹簧单元 COMBIN40和线性弹簧单元COMBIN14模拟，其中支座摩擦力及水平弹性回复力向采用 COMBIN40单元模拟，支座的竖向约束采用COMBIN14模拟。其中COMBIN40的参数设定如下：K1对应支座屈前刚度 K11减去屈后刚度K12、FSLIDE对应支座的屈服力、K2对应支座的屈后刚度K12，支座阻尼C1、间隙gap均设置为0。

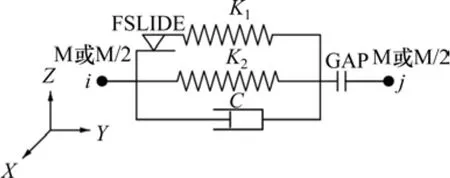
图5 COMBIN40力学模型Fig. 5 Mechanical model of COMBIN40

图6 COMBIN14力学模型Fig. 6 Mechanical model of COMBIN14

盆式活动支座的摩擦作用也可采用图4的双线性模型模拟，但屈后刚度取为0。

2 地震动输入

桥梁抗震设防烈度为7度，Ⅱ类场地土。非线性时程地震反应分析时，采用该桥桥址安评提供的3条人工合成地震波，加速度峰值为0.283 g，持时40 s。3条人工地震波采用同一目标反应谱，该目标反应谱是安评报告提供的罕遇地震场地加速度反应谱。图 5为 3条人工地震波加速度反应谱与目标谱。

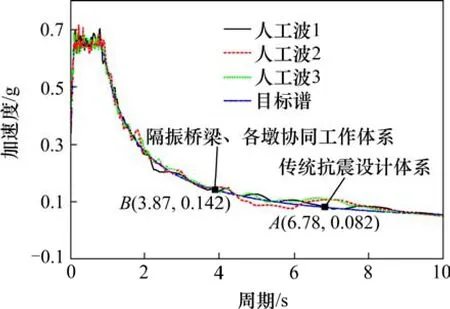
图7 3条人工波加速度反应谱Fig. 7 Acceleration response spectrum for three simulated earthquake waves

3 减隔震研究

大跨连续梁通常采用承载能力较高的盆式橡胶支座。为适应温度变化及混凝土收缩徐变的影响，全桥仅设置1个制动墩，通过制动墩与活动墩支座的摩擦力共同抵抗动力，以满足正常使用。在高烈度地区，由于只有1个制动墩，地震时上部结构质量激发的惯性力主要由制动墩承担，制动墩及基础的抗震问题比较突出。按照增加控制截面尺寸、调整截面配筋的传统抗震设计方法很难满足现行桥梁抗震设计规范的要求，需进行减隔震设计[11]。

3.1 设置液体黏滞阻尼器

桥梁结构中安置阻尼器可以增加结构的阻尼，在地震中耗散振动能量，从而减少桥梁结构的受力，减少桥梁的位移，也就很好地改善了桥梁的抗震能力[9,12]。

由式(1)知阻尼系数C和阻尼指数α是阻尼器设计的2个重要设计参数，C的取值对阻尼力F的影响较大，α的取值直接影响阻尼器的减震效果。对于该桥，经计算分析发现，在活动墩处各设置1个黏滞阻尼器的减震效果最为明显。本文分析研究了α分别取0.3，0.4，0.5，0.6，0.8和1.0，C分别取500，1 000，1 500，2 000，2 500和3 000下顺桥向设置4个黏滞阻尼器的减震效果，其中顺桥向地震作用下阻尼器的最大阻尼力、最大冲程与阻尼系数的变化关系如图8和图9所示，11号制动墩墩底的纵向弯矩、14号活动墩墩底的纵向弯矩如图 10和图11所示。

图8 不同阻尼器参数对阻尼器最大阻尼力的影响Fig. 8 Influence of different damper parameters on the maximum force of the damper

从图8可以看出阻尼器的最大阻尼力随阻尼系数C的增大而增大，随阻尼指数α的增大而减小，从图10可以看出11号制动墩墩底的纵向弯矩随阻尼系数C的增加而减少，随阻尼指数α的增大而增大，从图11可以看出14号活动墩墩底纵向弯矩随阻尼系数C的增大而增大，随阻尼指数α的增大而减小，这是因为黏滞阻尼器激发的阻尼力加强了活动墩与主梁间的约束，使地震作用在各墩间又进行了一次重分配。随着阻尼系数C的增大，阻尼指数α的减小，阻尼力越来越大，而活动墩与主梁间的约束逐渐加强，从而自由墩弯矩逐渐增大、制动墩弯矩逐渐减小。综合考虑在地震作用下各墩的受力情况，及阻尼器的输出力情况，建议阻尼指数α取0.3，阻尼系数C取2 000 (kN·s/m)0.3。(取该参数数时，固定墩受力、各墩墩梁相对位移均处于合理范围)

图9 不同阻尼器参数对阻尼器冲程的影响Fig. 9 Influence of different damper parameters on the stroke of the damper

图10 不同阻尼器参数对制动墩墩底纵向弯矩的影响Fig. 10 Influence of different damper parameters on bending moment at the bottom section of the braking pier

3.2 设置双曲面球型减隔震支座

国内外目前常用的减隔震支座主要包括高阻尼橡胶支座、铅芯橡胶支座、滑动摩擦型钢支座 3种[13]。双曲面球型减隔震支座是滑动摩擦型支座中的1种。与橡胶类减隔震支座相比，双曲面球型减隔震支座具有构造简单、承载力大、耐久性好等优点，双曲面球型减隔震支座的屈服刚度与作用于支座的竖向力及曲率半径有关，因此可以通过支座的曲率半径方便的调整屈服刚度，使各墩协调抗震[14-15]。

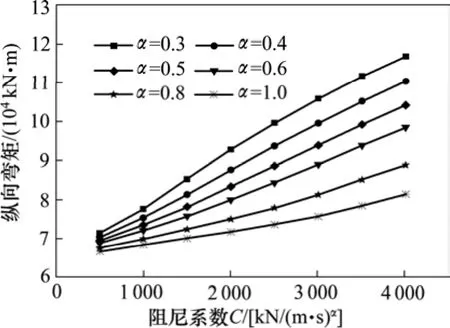
图11 参数对14号活动墩墩底纵向弯矩的影响Fig. 11 Influence of different damper parameters on bending moment at the bottom section of the pier No.14

滑动球面和转动球面的球心距 H以及滑动球面的球心摩擦因数μ是影响双曲面球型减隔震支座减震效果的2个主要设计参数。本文分析比较了在各墩设置双曲面球型减隔震支座，摩擦因数分别取0.01，0.02，0.03，0.04，0.05，0.07 和 0.1，9 号，15号过渡墩支座的球心距取一般值 1.5 m，10～14号墩上支座的球心距分别取 3.6，4.8，6.0，7.2和8.4 m，+∞ m(当H趋于+∞时，屈后刚度趋于0)在顺桥向强震作用下，11号墩的剪力键失效，11号墩支座发生摆动，单制动墩体系转化为各墩协同抗震体系，11号墩的墩梁相对位移响应、墩底弯矩响应如图12～13所示。

通过支座参数分析可知：

①相同摩擦因数条件下，球心距H越小，该支座的屈后刚度越大，梁与墩之间的约束越强，从而桥墩内力越大，墩梁相对位移越小。

②相同球心距条件下,地震响应随摩擦因数的变化规律较为复杂，本文分2类情况进行讨论：

(i)当8.4 m≤H＜+∞ m时，支座的屈后刚度较小，水平回复力较小,从而支座的水平力大部分由摩擦力提供(当H趋于+∞ m时，支座水平力完全由摩擦力提供)，随着μ的增大，上部结构通过摩擦力传递到桥墩的剪力会越大，从而增大了桥墩墩底弯矩。

(ii)当3.6 m≤H＜8.4 m时，随摩擦因数的增大，墩底弯矩先增加后减小再增大，之所以会出现墩底弯矩随摩擦因数增大而减小的现象，可能是因为当μ增大至一定程度时，由支座传递下来的水平剪力与墩身振动产生的剪力方向相反，从而抵消减小了墩底内力，也可能是支座水平力引起了墩身自振周期的变化，使得周期的变化朝着地震衰减的方向，降低了墩的地震响应，并且这种减小大于上部质量经支座传下来的水平力；从图中可以看出当摩擦因数超过一定限度后，墩底内力会继续呈现增大的趋势，这是由于上部结构的惯性力会通过较大的支座水平力传递到桥墩，对下部结构产生不利影响，设计中应该尽量避免。

图12 不同支座参数对11号墩墩梁相对位移的影响Fig. 12 Influence of different bearing parameters on displacement between beam and pier No.11

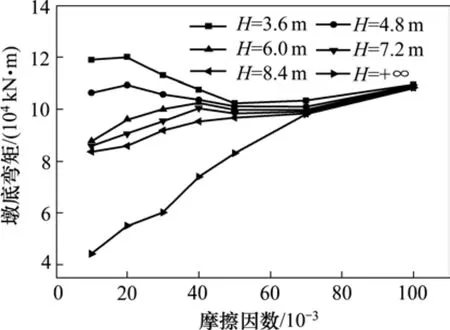
图13 不同支座参数对11号墩底纵向弯矩的影响Fig. 13 Influence of different bearing parameters on bending moment at pier No.11

综合考虑支座参数对各墩墩底地震内力响应的影响，及对各墩支座位移的影响，建议摩擦因数μ取0.04，球心距H取3.6 m。(取该参数时，各墩受力最为均匀、各墩支座位移值均处于合理范围内)

由于剪力键失效前，全桥体现为单制动墩抗震体现，剪力键设计时基于剪力键失效前各墩的地震弯矩不应大于失效后各墩的地震弯矩的原则。该联桥的制动墩剪力键水平极限承载能力取为 2 200 kN，可满足制动力下的正常使用要求。

3.3 减隔震设计方案对比

为了进一步比较2种减隔震方案中最优参数组合(液体黏滞阻尼器方案C=2 000，α=0.3；双曲面球型减隔震支座方案：μ=0.04，H=3.6)的减震效果，本文利用 UCFyber软件对桥墩墩底截面进行截面弯矩-曲率分析计算出各墩的等效屈服弯矩、并给出了在罕遇地震作用下，各方案的结构地震响应对比，如图14～17所示。

图14 2种减震方法下各墩底弯矩对比Fig. 14 Comparison of bending moment at the bottom section of piers

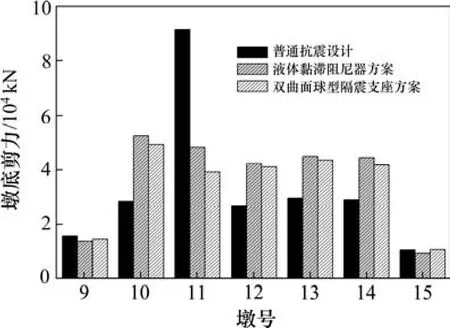
图15 2种减震方法下各墩底剪力对比Fig. 15 Comparison of shear force at the bottom section of each pier

图16 2种减震方法下各墩梁相对位移对比Fig. 16 Comparison of relative dispalcement between beam and piers

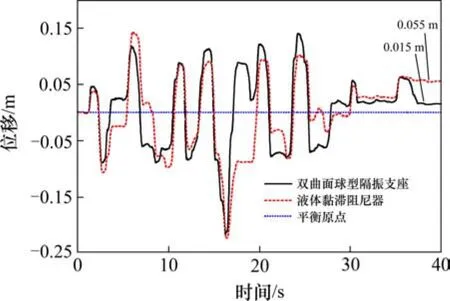
图17 2种减震方法下14号墩墩梁相对位移对比Fig. 17 Comparison of relative displacement between beam and pier No.14

从图14～17可以看出：

1) 液体黏滞阻尼器方案中制动墩墩底弯矩减小了约53%，墩底剪力减小了约47.3%，6个活动墩墩底弯矩分别增大了约-7%，126%，59%，84%，86%和-13%，墩底剪力分别增长了约-12%，84%，59%，52%，53%和-12%；而采用双曲面球型隔震支座方案时，制动墩墩底弯矩减小了约61%，墩底剪力减少了约57%，6个活动墩墩底弯矩分别增长了约-12%，113%，57%，75%，66%和-14%，墩底剪力分别增加了约-8%，74%，54%，47%，45%和2%，各墩地震力分配更趋均匀、合理。

2) 与传统抗震方案相比，采用液体黏滞阻尼器方案时，6个活动墩的墩梁相对位移分别减少了约45%，44%，59%，57%，56%和56%；而采用双曲面球型隔震支座方案时，6个活动墩的墩梁相对位移分别减少了约 64%，46%，63%，60%，60%和81%，双曲面球型隔震支座更能有效地控制各墩墩梁相对位移。

3) 液体黏滞阻尼器方案中，14号活动墩的支座残余变形约为 0.055 m，残余变形较大，不利于震后的修复，而采用双曲面球型隔震支座方案时，其残余变形约为 0.015 m，双曲面球型隔震支座能更有效地控制支座的震后残余变形，有利于震后的修复。

4 结论

1) 位于高烈度区的长联多跨连续梁桥，若采用传统的抗震设计，制动墩的地震响应较大，采用减隔震设计则可有效提高其抗震性能 。

2) 长联多跨连续梁桥设置液体黏滞阻尼器进行减隔震设计，减震效果随阻尼系数C的增大而减小，随阻尼指数α的增大而增大；阻尼器的阻尼力随C及α的增加而增加，阻尼器的最大冲程随阻尼系数C的增大而减小，随阻尼指数α的增大而增大。

3) 设置液体黏滞阻尼器与传统抗震设计相比较，制动墩的纵向弯矩，及活动墩的墩梁相对位移均得到了较好的控制，制动墩底弯矩减小超过50%，活动墩墩梁相对位移减少超过44%，但由于黏滞阻尼器不具备自复位功能，震后修复难度大。

4) 长联多跨连续梁桥设置双曲面球型隔震支座，能使各墩较均匀的分担地震荷载，自身抗震性能充分发挥，与传统抗震设计相比较，制动墩墩底弯矩减少超过60%，活动墩墩梁相对位移减少超过45%，且具有自复位功能，降低了震后的修复难度。

5) 对位于高烈度区的长联多跨连续梁进行减隔震设计的措施有多种，合理选择减隔震方法及相关参数能有效地控制结构的地震响应，从而满足现行抗震设计规范的要求。针对本文研究对象，从减隔震效果及经济因素考虑，最终选择双曲面球型减隔震支座。

参考文献：

[1] 陈列, 胡京涛. 桥梁隔震技术[M]. 北京: 中国铁道出版社, 2014.

CHEN Lie, HU Jingtao. Seismic isolation technology of bridge[M]. Beijing: China Railway Press, 2014.

[2] 叶爱君. 桥梁抗震[M]. 北京: 人民交通出版社, 2002.

YE Aijun. Seismic design of bridge[M]. Beijing: China Communication Press, 2002.

[3] Symans M D, Charney F A, Whittaker A S, et al. Energy dissipation systems for seismic application: Current practice and recent developments[J]. Journal of Structural Engineering, 2008, 134(1): 3-21.

[4] 曾武华, 孙海朋, 卓卫东. 早期大跨径连续梁改造中的抗震方案比选[J]. 福州大学学报(自然科学版), 2013,41(4): 505-509.

ZENG Wuhua, SUN Haipeng, ZHUO Weidong. Seismic scheme comparison in reconstruction design of an early long span continuous girder bridge[J]. Journal of Fuzhou University (Natural Science Edition), 2013, 41(4): 505-509.

[5] 姜冲虎, 李德建. 大跨度连续梁桥SSAB与FVD组合应用减隔震技术研究[J]. 铁道科学与工程学报,2013(6): 28-32.

JIANG Chonghu, LI Dejian. Seismic isolation technology research of long-span continuous beam bridge with SSAB and FVD[J]. Journal of Railway Science and Engineering,2013, 10(6): 28-32.

[6] 夏修身, 陈兴冲, 王希慧, 等. 剪力键对隔震桥梁地震反应的影响[J]. 地震工程与工程振动, 2012, 32(6):104-109.

XIA Xiushen, CHEN Xingchong, WANG Xihui, et al.Effect of shear keys on seismic response of bridge using isolation bearings[J]. Earthquake Engineering and Engineering Vibration, 2012, 32(6): 104-109.

[7] YUAN Wancheng, WANG Binbin, Cheung P, et al.Seismic performance of cable-sliding friction bearing system for isolated bridge[J]. Earthquake Engineering Vibration, 2012, 11(2): 173-182.

[8] TB 10002.5—2005, 铁路桥涵地基和基础设计规范[S].TB 10002.5—2005, Code for design on subsoil and foundation of railway bridge and culvert[S].

[9] 陈永祁. 桥梁工程液体黏滞阻尼器设计与施工[M]. 北京:中国铁道出版社, 2012.

CHEN Yongqi. Design and construction of fluid viscous devices for shock control of bridges[M]. Beijing: China Railway Press, 2012.

[10] 刘俊. 高烈度区多跨刚构连续梁桥减隔震设计研究[J].铁道工程学报, 2013(5): 40-46.

LIU Jun. Research on seismic isolation design of multi-span rigid frame-continuous girder bridge in high seismic intensity area[J]. Journal of Railway Engineering Society, 2013(5): 40-46.

[11] 毛玉东, 李建中. 大跨度连续梁桥延性和减隔震设计[J]. 桥梁建设, 2016(3): 92-97.

MAO Yudong, LI Jianzhong. Ductility and seismic mitigation and isolation design of long-span continuous girder bridges[J]. Bridge Construction, 2016(3): 92-97.

[12] 宋子威, 蔡小培. 粘滞阻尼器在高速铁路长联大跨连续梁中的应用[J]. 清华大学学报(自然科学版), 2012,52(8): 1102-1105.

SONG Ziwei, CAI Xiaopei. Application of viscous damper devices to the seismic design of long span and long unit continuous girder bridges on high-speed railway[J]. Journal of Tsinghua University (Science and Technology), 2012, 52(8): 1102-1105.

[13] Dion C, Bouaanani N, Tremblay R, et al. Real-time dynamic substructuring testing of viscous seismic protective devices for bridge structures[J]. Engineering Structures, 2011, 33(12): 3351-3363.

[14] Kelly T E. Base isolation of structures-design guidelines[R]. Wellington: Holomes Consulting Group Ltd, 2001.

[15] Tsai C, Chiang T, Chen B. Finite element formulations and theoretical study for variable curvature friction pendulum system[J]. Engineering Structure, 2003, 25:1719-1730.