地铁隧道矿山法施工事故风险分析与评价

郑涛，孙捷城，王国富,

随着我国社会经济突飞猛进的发展，城市轨道交通的建设方兴未艾，自 1969年北京修建了我国第1条地铁线路以来，天津(1976)、上海(1995)、广州(1997)、长春(2002)等城市陆续开始城市地铁的建设。到2013年底，我国已修建地铁线路87条，且运营里程达2 539 km，与此同时，有36座城市获批修建城市地铁线路。《“十二五”综合交通运输体系规划》指出，截止到 2016年，全国城市地铁建设里程已达4 000 km，迎来地铁修建的高潮，且今后几年每年增长里程在500 km左右[1]。根据目前各城市建设情况，估计到 2020年左右，我国城市地铁运营里程将达到6000 km。此外，与其他交通工具相比，地铁具有安全可靠、方便快捷、舒适环保、运能大以及用地省等优点[2]。但不可否认的是，在中国城市地铁迅猛发展的同时，其施工过程频发的各种安全事故为其蒙上了不小的阴影，如2003-07-01上海地铁某联络通道在施工期间发生大面积坍塌、防汛墙塌陷致使工期延误数年之久的特别重大事故，2007-03-28 02标苏州地铁发生坍塌事故，引发地面出现塌陷，致6人死亡[3]等。针对各种安全事故，国内众多学者对其进行分析和总结，侯艳娟等[4]基于北京地铁施工安全事故典型案例，根据事故发生原因将安全事故分为5类，并针对每一类事故给出相应的防治策略与方案，同时提出适合中国国情的安全控制和风险管理措施。李凤伟等[5]对2003～2010年地铁建设118起安全事故进行统计分析，指出塌陷和坍塌是主要事故类型，并对事故按区域、事件、类型等因素进行研究，提出死亡比率的概念以反映城市安全管理水平。罗伟[6]基于极限分析法研究浅埋隧道破坏原理，并且对其围岩压力计算表达式进行理论推导，通过非线性规划优化方法优化目标函数，分析浅埋隧道稳定性及其可靠度。杨远程[7]从人、机、料、环和管理等方面全面分析总结地铁施工期间风险源因素，并提出风险事故成因分析方法(RCTM)以及事故根源追溯方法。钱七虎[8]全面介绍了我国当前地下工程建设所面临的挑战，并对事故发生原因进行了深入分析，明确指出主观原因和责任事故是地下工程安全事故的主要原因，最后给出事故预防的技术方法和管理手段。杨晨等[9]基于深圳地铁安全事故统计，指出坍塌是地铁工程施工期的多发事故，并从基坑工程、盾构工程、矿山法开挖以及高支模架施工4个方面分别介绍事故特点与预防措施。城市地铁属于万众瞩目的工程，在网络日益普及的今天，一旦出现安全事故，极可能造成不可估量的社会影响和极大的舆论压力。因此，准确分析城市地铁施工期间风险事故原因，研究其结构的可靠度是一个非常重要的课题。在前人研究的基础上，本文对国内近十年来100起地铁建设期安全事故进行深入分析，并结合青岛地铁某典型事故案例，运用可靠度理论以及FLAC3D软件分析地铁隧道的稳定性，最后给出了风险事故控制及地铁隧道施工稳定性的相关建议，以供相关技术人员参考。

1 安全事故统计

通过分析我国近10年来100起地铁隧道矿山法建设施工期所发生的安全事故样本发现[3]，该样本包含坍塌事故 55起，由各种机械伤害引起的事故11起，火灾与水灾诱发事故各7起，坠物击打引起事故6起，模板坍塌造成事故5起，爆炸引发事故4起，由其他方面原因导致事故5起，详细数据统计如表1及图1所示[10]。对于各类事故造成的人员伤亡方面，坍塌占总伤亡人数的55.9%，具体数据参考表1与图2。通过对上述各类事故数据统计分析可知，坍塌是地铁隧道工程建设期的多发多害事故，是重点防备的事故类型。

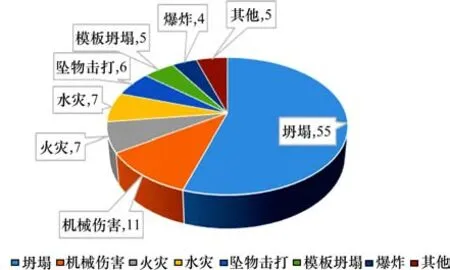
图1 安全事故统计Fig. 1 Accidents statistics

表1 安全事故统计(按事故类型划分)Table 1 Accidents statistics (Classification by accident type)

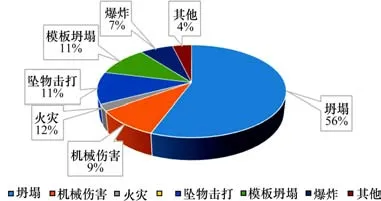
图2 伤亡人数比例Fig. 2 Proportion of casualties

2 可靠度理论分析

由于大量事故以及人员伤亡是坍塌引起的，所以对坍塌事故进行深入研究是一个非常重要的课题。作为极其复杂的地下工程，城市地铁隧道周边地层条件千差万别，且受力由于现场实际情况的不同而存在较大差异，故造成坍塌事故的因素有很多，但归其本质最根本的原因是由于岩土体参数的变化，若采用传统的确定性安全系数对岩土体强度参数进行分析，误差较大，在工程实际中将倾向于应用考虑岩土体不确定性可靠度分析方法。本文通过强度折减法(c和 φ 值分别取不同的折减系数)[11-12]与点估计法[13]分析地铁隧道的可靠度，更好地避免坍塌事故发生，并且通过FLAC3D有限差分软件，对青岛地铁3号线某起典型坍塌案例进行深入分析，得到引起坍塌事故的原因，以便更好地指导同类轨道交通的建设。目前对于地铁隧道可靠度研究的方法较多[14]，较为常用的有一次二阶矩法、渐进积分法、响应面法、Momte Carlo法和点估计法等。一次二阶矩法需将分布函数展开成Taylor级数，且不能考虑设计点附近的局部性质，产生较大误差；渐进积分方法需对基本变量概率密度函数对数的一阶二阶导数进行求导计算，使问题的繁琐程度有所增加；随机响应面方法通过插值展开点和系数进行调整，计算过程复杂；Momte Carlo方法需要重复模拟过程，工作量较大。点估计法是Daniels[13]提出一种可靠度计算方法，且该方法不必预先分析随机变量的分布类型，只需计算出随机变量的均值和方差，便可求出分布函数的一阶矩(均值)和二阶矩(方差)，由此得到地铁隧道的可靠指标和破坏概率。该方法计算过程简单，并且计算结果与实际情况相符合，是一种较实用的可靠度分析方法。

点估计法无需考虑分布函数的变化形态，可直接选取变量的均值±标准差，来构建基本取值点。在地铁隧道施工过程中，隧道稳定性受到岩土体强度参数、外加荷载、施工环境的影响，而对于强度折减法主要考虑对地铁隧道可靠度影响较大的岩土体强度指标c和φ 值[15]，相应的取值有：

式中：μc，μφ，σc，σφ为 c和 φ 值的均值和标准差。

建立数值分析模型，对于每一组随机参数的组合，采用对岩土体强度参数(c和 φ 值)的折减得到隧道拱顶特征点的位移与折减系数关系曲线[16]，将曲线上突变的拐点作为安全系数，得到1组对应的隧道围岩安全系数如式(2)，由式(3)～(6)可计算出隧道安全系数的均值μF，标准差σF，可靠度指标β以及失稳破坏概率Pf，进而评价隧道工程的可靠度。

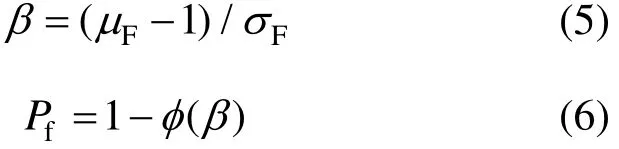
式中：()φβ为标准正态分布函数，可在标准正态分布表中查询。

3 工程实例分析

3.1 事故概况

2012-04-25凌晨突降大雨，青岛地铁3号线某区间由于雨水渗入掌子面前方的土体，引起掌子面涌水、涌砂、突泥，进而发生隧道坍塌冒顶事故。此事故诱发地面坍塌范围约15 m×15 m，坍塌深度约为8 m，并且造成4条高压电缆受损，部分砂土、各种杂物涌入隧道，造成大面积浸水，如图3所示。由于工作人员发现较早，抢险及时，未引起人员伤亡情况，但坍塌段位于青岛市交通干道，人流量较大，引起较多市民围观，产生极坏的社会负面影响。

事故原因如下：坍塌区隧道围岩为富水砂层，在其开挖前已经布设降水井进行降水，并且降水后地下水位已降至隧道底部以下，确保隧道开挖在无水环境下进行，但由于突降大雨，排放雨水的暗渠无法大量排水，导致暗渠转折处(即塌方位置)产生破裂，暗渠中的大量雨水涌入隧道上方土层，在雨水浸泡下，原来无水的隧道周围砂层内黏聚力下降、内摩擦角变小，整体强度变弱，自稳能力下降，掌子面发生涌水、涌砂现象，并导致地面发生冒顶事故。

图3 地面塌方部位Fig. 3 Ground collapse site

3.2 坍塌事故可靠度分析

塌方处隧道埋深约8 m，穿越地层岩性以砂土为主，采用上下台阶预留核心土方法开挖，数值计算模型分为回填土、砂土、上台阶、下台阶、核心土、上下台阶衬砌、强风化花岗岩、中风化花岗岩等9种模型单元，模型范围为52 m(横向)×10 m(纵向)×31 m(竖向)，对其四周进行水平约束，底面竖直方向约束，上边界为自由边界，各模型力学参数见表2，模型采用Mohr-Coulomb 弹塑性模型，即τ=c+σtanφ，f=tanφ，其模型如图 4 所示。

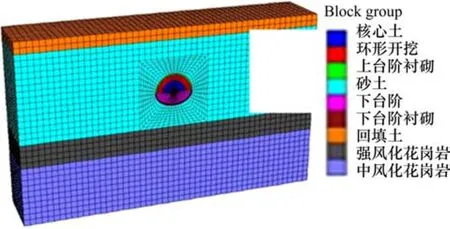
图4 数值计算模型建立Fig. 4 Numerical model

根据青岛地铁3号线专项设计资料中砂土的无侧限双轴实验知砂土峰值强度指标分别为 μc=40 kPa，μφ=45°，变异系数分别为 ξc=0.20，ξφ=0.15，则标准差分别为σc=8 kPa，σφ=6.75°。根据有限元强度折减法，将隧道围岩的强度参数值c和f除以一个折减系数Ftrial后得到1组ci和fi值，每一组ci和fi值输入到计算模型中进行计算，在c和f 值不断减小的过程中隧道的安全系数也随之降低，可以得到一组临界值c0和f0，即：当f≤f0和c≤c0时隧道将发生失稳破坏，f＞f0和c＞c0时隧道处于稳定状态。计算时：通过预设折减系数Ftrial进行逐次计算，得到隧道拱顶特征点的位移与折减系数(S-Ftrial)相对应的曲线，将曲线上突变的拐点作为安全系数Fn，故在不同强度参数组合条件下隧道的安全系数分别为：

由此求得隧道安全系数均值 μF=1.27，标准差σF=0.14，可靠度指标 β=1.91，失稳破坏概率Pf=1 - φ(1.91) = 2.81%，表明隧道处于稳定状态，数值计算结果显示，无水条件下隧道开挖后，最大竖向沉降35.3 mm，地表最大沉降约20 mm，见图5，满足《地铁工程监控量测技术规程》[17]中地面沉降控制值30 mm的要求，可以看作隧道处于安全状态。

表2 模型参数Table 2 Parameters of model

图5 竖向位移云图Fig. 5 Vertical displacement

由于突然出现大雨，年久失修的地下排水暗渠因不堪重负而发生破裂，致使大量雨水入渗隧道上方地层，回填土、砂土逐渐趋于饱和状态，强度急剧下降，基本丧失自稳能力，部分雨水甚至通过掌子面进入隧道内，最终导致掌子面出现涌水涌砂现象，同时隧道上覆土体发生坍塌，地面出现冒顶。根据刘波模型试验中关于干性土体与饱和土体参数取值研究[18]，土体饱和后，密度稍有上升，强度参数下降约58%。回填土、砂土的力学参数为干燥时参数的一半，中风化花岗岩与衬砌力学参数选用原先数值，见表3。

表3 饱水状态下模型参数Table 3 Parameters of model under water saturated state

此时，根据现场评估资料知，砂土峰值强度指标分别为 μc=24 kPa，μφ=20°，变异系数分别为ξc=0.23，ξφ=0.17，则标准差分别为 σc=5.52 kPa，σφ=3.4°。通过有限元强度折减法得其安全系数为：

按照上述分析方法隧道安全系数的均值μF=1，标准差σF=0.14，可靠度指标β=0，隧道失稳破坏概率Pf=1 - φ(0) = 2.81%，表明隧道处于失稳状态，由数值模拟结果显示饱水状态下，最大竖向沉降达377.8 mm，地表最大沉降约150 mm，远远超过《地铁工程监控量测技术规程》[17]中地面沉降控制值30 mm的要求，可看作已出现坍塌事故。

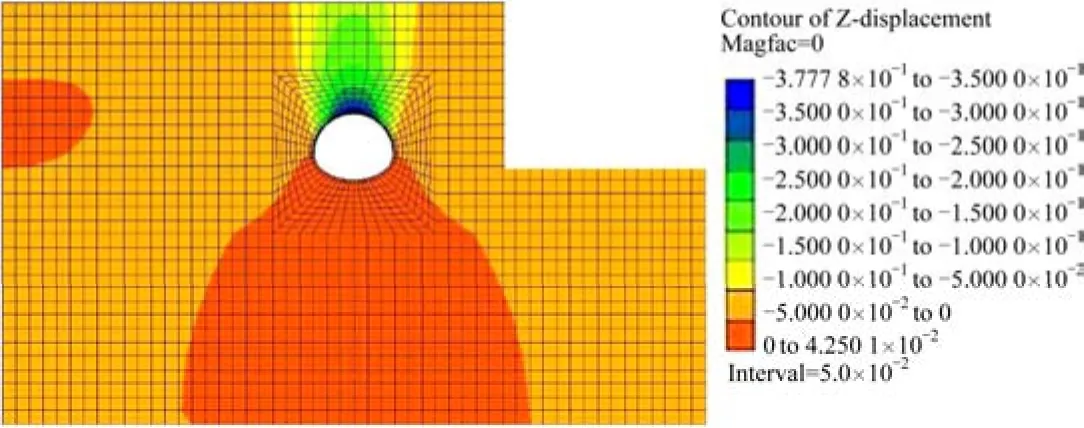
图6 饱水状态下最大竖向位移云图Fig. 6 Vertical displacement under water saturated state

4 结论

1) 城市地铁工程建设施工期坍塌事故占据了安全事故的一半，产生了较大的人员伤亡以及经济损失，并且延误了工期，通过可靠度分析方法与数值模拟计算分析坍塌原因，得到岩土体强度参数对坍塌有着直接影响。

2) 通过有限元强度折减法与点估计方法相结合研究地铁隧道结构的可靠性，在考虑土体参数的变异性的基础上，避免了计算的复杂性，可为类似工程分析提供参考。

3) 青岛地铁 3号线在某隧道未受雨水影响时安全系数均值为1.27，可靠度指标达1.91，处于稳定状态，在雨水渗入地层以后，围岩强度降低，自稳能力变差，在施工扰动后隧道安全系数均值为1，可靠度指标为0，隧道坍塌，与实际情况一致。

参考文献：

[1] 国务院. “十二五”综合交通运输体系规划[Z]. 综合运输, 2012-07-25.

State Council. “Twelve Five Year Plan” integrated transport system[Z]. Comprehensive Transportation,2012-07-25.

[2] 温树东. 城市轨道交通建设安全评价与分析[D]. 大连:大连交通大学, 2014.

WEN Shudong. Urban rail transit construction safety evaluation and analysis[D]. Dalian: Dalian Jiaotong University, 2014.

[3] 张顶立. 城市地下工程建设安全风险及其控制[M]. 北京: 化学工业出版社, 2012: 77-78.

ZHANG Dingli. Safety risks and corresponding control measures of urban underground engineering construction[M]. Beijing: Chemical Industry Press, 2012: 77-78.

[4] 侯艳娟, 张顶立, 李鹏飞. 北京地铁施工安全事故分析及防治对策[J]. 北京交通大学学报(自然科学版), 2009,33(3): 52-59.

HOU Yanjuan, ZHANG Dingli, LI Pengfei. Analysis and control measures of safety accidents in beijing subway construction[J]. Journal of Beijing University (Science and Technology), 2009, 33(3): 52-59.

[5] 李凤伟, 杜修力, 张明聚. 铁道工程建设施工事故统计分析[J]. 地下空间与工程学报, 2014, 10(2): 474-479.

LI Fengwei, DU Xiuli, ZHANG Mingju. Statistical analysis of accidents in metro construction[J]. Chinese Journal of Underground Space and Engineering, 2014,10(2): 474-479.

[6] 罗伟. 浅埋偏压隧道稳定性分析及其可靠度研究[D].长沙: 中南大学, 2014.

LUO Wei. Stability analysis and reliability research on the shallow tunnel under unsymmetrical pressure[D].Changsha: Central South University, 2014.

[7] 杨远程. 地铁施工安全事故分析与评价方法研究[D].武汉: 华中科技大学, 2009.

YANG Yuancheng. Study on the analysis & evaluation methods of metro construction accidents[D]. Wuhan:Huazhong University of Science and Technology, 2009.

[8] 钱七虎. 地下工程建设安全面临的挑战与对策[J]. 岩石力学与工程学报, 2012, 31(10): 945-1956.

QIAN Qihu. Challenges faced by underground projects construction safety and countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(10): 1945-1956.

[9] 杨晨, 张佐汉. 深圳地铁二期工程建设期安全事故分析[J]. 铁道建筑, 2013, 45(4): 45-48.

YANG Chen, ZHANG Zuohan. Shenzhen metro phase II project analysis of security incidents[J]. Railway Engineering, 2013, 10(1): 45-48.

[10] 胡群芳, 秦家宝. 2003～2011年地铁隧道施工事故统计分析[J]. 地下空间与工程学报, 2013, 9(3): 705-710.

HU Qunfang, QIN Jiabao. Statistical analysis on accidents of subway tunnel construction from 2003 to 2011 in China[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(3): 705-710.

[11] Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387-403.

[12] Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique,1999, 49(6): 835-840

[13] Daniels H E. Saddlepoint approximations in statistics[J].Annel Mathematics Statistics, 1954, 25(4): 631-650.

[14] 张明, 金峰. 结构可靠度计算[M]. 北京: 科学出版社,2015.

ZHENG Ming, JIN Feng. Structural reliability computations[M]. Beijing: Science Press, 2015.

[15] 李杰. 基于可靠度方法的既有铁路边坡稳定性分析[J].铁道工程学报, 2014, 185(2): 33-37.

LI Jie. Slope stability analysis of the existing railway based on the reliability method[J]. Journal of Railway Engineering Society, 2014, 185(2): 33-37.

[16] 张黎明, 郑颖人, 王在泉, 等. 有限元强度折减法在公路隧道中的应用探讨[J]. 岩土力学, 2007, 28(1): 97-101.

ZHANG Liming, ZHENG Yingren, WANG Zaiquan, et al.Application of strength reduction finite element method to road tunnels[J]. Rock and Soil Mechanics, 2007, 28(1):97-101.

[17] DB11/490—2007, 地铁工程监控量测技术规程[S].DB11/490—2007, Technical code for monitoring measurement of subway engineering[S].

[18] 李涛, 刘波, 李岩, 等. 基于微观结构的饱和红黏土孔隙比计算[J]. 中国矿业大学学报, 2011, 40(5): 720-725.

LI Tao, LIU Bo, LI Yan, et al. The void ratio of saturated red clay calculated from a micro-structure model[J].Journal of China University of Mining & Technology,2011, 40(5): 720-725.