扭转荷载下嵌岩桩的扭转特性研究

程昊，刘齐建

桩基础是常见的基础形式，能承受由风、海浪和车辆等偏心荷载产生的扭转荷载。自20世纪60年代以来，国内外学者做了很多关于受扭桩的研究，现有研究方法大致分为3类：试验方法、数值计算法和解析法。关于桩的扭转试验方法，Stoll[1]开展了静扭转荷载下圆形摩擦桩桩周剪力的试验。Novak等[2]进行了桩基础在动扭转荷载下的试验。Kong等[3]通过群桩扭转试验研究，得到了基桩扭矩与水平位移的相互影响规律。关于桩扭转特性的数值计算法，Tham等[4]采用边界元法分析了桩的动扭转特性。ZHANG等[5]采用3D有限元方法，研究了桩在静扭转荷载下的响应。Militano等[6]采用 Laplace变换，研究了多层土中桩的瞬态扭转响应。在解析法方面，Novak等[7-9]采用了分离变量法研究了扭转和水平荷载作用下单桩的响应。Misra等[10]采用最小势能原理研究了多层土中单桩在静扭转荷载下的响应。王奎华等[11-12]在Novak的基础上进行了改进，研究了单桩在均质地基中的扭转振动特性。王海东等[13]研究了层状地基中桩的扭转动力阻抗的问题。王国才等[14]通过建立层状地基的刚度矩阵，求解了层状地基中单桩的扭转振动问题。本文拟对单桩扭转阻力特性展开深入研究。首先，利用分离变量法求解土的扭转平衡方程，得到桩-土系统扭转位移。其次，采用虚功原理对土层进行分析，得到扭矩的显式表达式。最后，根据嵌岩桩的扭转平衡方程与边界条件得到桩的扭转位移与刚度。

1 基本假设与土层平衡方程求解

1.1 计算模型

本文计算模型及坐标系如图3.1所示。土视为各向同性、均质的弹性介质，厚度为H，密度为ρs，剪切模量为μs。嵌岩桩半径为r0，剪切模量为μp，扭转惯性矩 Jp= π r04/2，密度为ρp。桩顶荷载仅考虑纯扭矩T，以便得到解析解。在圆柱坐标系下，本计算模型可简化为反轴对称问题。

图1 计算模型Fig. 1 Calculation model

本文采用如下计算假定：

1) 桩身与桩周土紧密接触，无相对滑动。该假定仅针对桩顶扭矩较小情况适用，当扭矩较大时，桩土界面将出现塑性变形或滑移。

2) 忽略桩-土系统竖向及径向位移，仅考虑切向位移。

1.2 位移模式

由于反对称性，桩-土系统切向位移v(r, z)只与竖向坐标z及径向坐标r有关，设为：

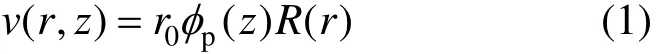
式中：p()zφ表示桩身沿深度的扭转角；R(r)表示系统位移沿径向的衰减函数，需满足以下边界条件

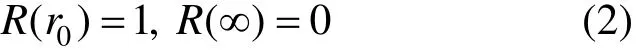
可见，在r=r0处，桩土系统位移等于桩周位移，即在桩土交界处，桩土位移协调；当r=∞，桩土系统位移为0。

1.3 土体平衡方程与求解

由于桩-土系统只受到扭矩荷载作用，径向与竖向位移可以忽略，则土层的平衡方程可简化为

将式(1)代入式(3)中，得

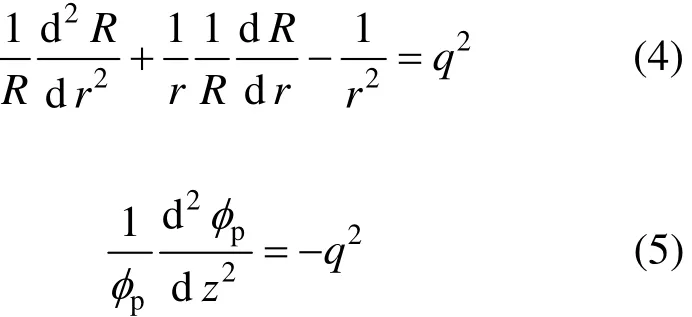
式中：q为待定常数。

求解式(4)与(5)可得

式中：A1，B1，A2和 B2为待定常数；K1和 I1分别表示第1阶第1类、第2类修正Bessel函数。

当0r→∞时，系统位移趋向于0，根据Bessel函数的性质，可知A1=0。另外，土层上表面为自由表面，剪应力 τzθ=0，可知 A2=0。

将式(6)和(7)代入式(1)中，并结合边界条件，可得系统位移为

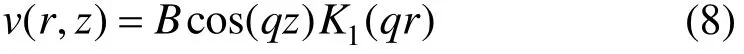
其中：系数B为包含了B1及B2的常数。

考虑到衰减函数的性质0()1Rr = ，式(8)需调整为

其中：C为包含了B和10( )K qr的待定系数。

2 桩侧扭矩求解

为了得到土对桩的扭矩表达式，取厚度为 dz的土环进行分析。当系统只有切向位移时，反轴对称问题的应力和应变为

其中应变为

土环中外力所做功Ue为

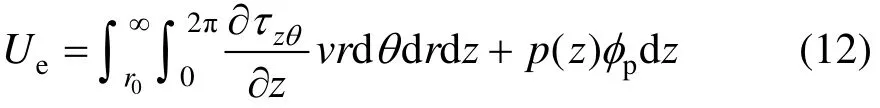
其中：p(z)为土层对桩的作用扭矩。

内力做功Ui为

由最小势能原理，可得

将式(1)、(10)～(13)代入式(14)，收集pδφ项，可得土对桩的扭矩p(z)为

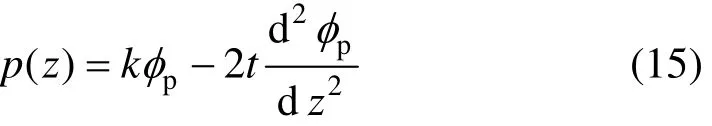
其中：系数k和2t为

3 嵌岩桩扭转分析

3.1 桩的扭转控制方程

桩的扭转平衡方程为

其中：T(z)为沿桩身的外荷载，可由桩顶荷载T通过Fourier展开得到。

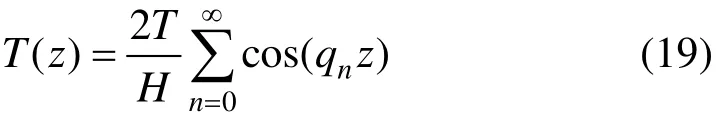
其中：系数qn可由桩的边界条件确定。

3.2 嵌岩桩的解答

由于土层底部的位移为0，可得qn为

将qn代入式(9)中得

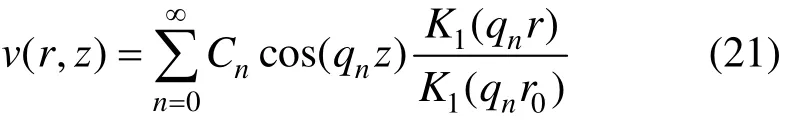
结合式(1)与(21)，可得桩的扭转角与第n阶模态衰减函数分别为

将式(22)和(23)分别代入式(15)～(17)中得

式(24)表示了扭矩与桩扭转角之间的关系，又可以写为

其中：αn是第n模态下土对桩作用扭矩的抵抗系数，

其中：系数kn和2tn可通过式(16)和(17)得到

将式(19)、(22)和(24)代入式(18)中，得

将Cn代入式(22)中，可得桩的扭转角为

桩-土系统的刚度K为

3.3 无量纲化处理

引入以下无量纲量

无量纲抵抗系数αn可表示为

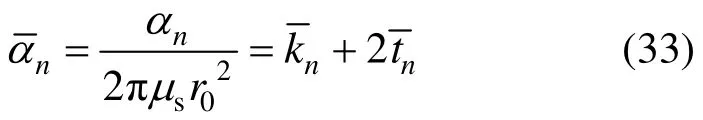
其中

无量化扭转角及刚度为

其中：γ=4/μ。

4 结果验证

为验证本文正确性，将本文解答与Misra等[10]的理论解及其有限元结果进行对比，如图2所示。计算时，H=10 m，r0=0.5 m，桩剪切模量μp=9.6×106kPa，土剪切模量 μs=2×104kPa，T=100 kN·m。

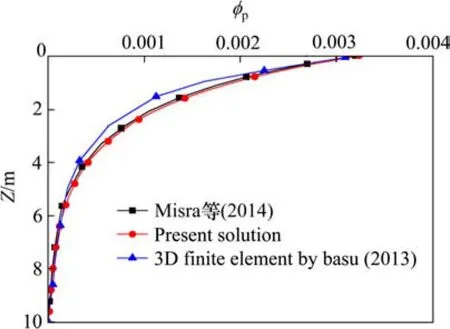
图2 本文结果与已有解答对比Fig. 2 Comparison of the results by the present solution with those by the available solutions

由图2可知，本文结果与已有理论解及有限元解结果吻合良好。

5 参数分析

5.1 扭矩的阐述

由式(15)可知，扭矩由2个部分组成，分别由k与2t来表征。

从物理意义上来看，k项表示的是一个Winkler弹簧，其扭矩与扭转角成正比，由剪应力τrθ提供。2t表示的是薄膜，其扭矩与扭转角2阶导成正比，由 τzθ提供。

5.2 不同模态抵抗系数αn

图3给出了αn及其组成部分随模态数n的变化。由图3可知，低模态时，抵抗系数αn主要由k项提供，2t项所占比例很小。随着模态数增大，2t所占比例慢慢增大，但是其所占比例始终小于k项。

图3 抵抗系数随模态数的变化Fig. 3 Variation of αnwith n

5.3 扭矩组成及参数分析

由式(15)，可将扭矩p(z)表示为2部分之和

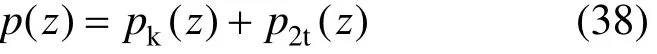
其中

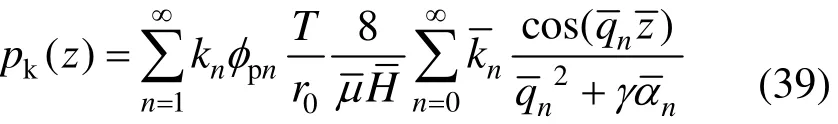
图4给出了pk与p2t沿桩身分布情况。可以看出，在桩顶，pk约为p2t的8～10倍，沿深度方向2项都逐渐减小。到达桩底时，pk与p2t均为0。

图5 给出了pk随长细比H/r0和桩土模量比μ的变化关系。可以看出，随长细比增大，pk增大，且在长细比约为 40以后趋于稳定。这说明当桩长达到一定数值后，靠增加桩长来提高抗扭阻力中的pk部分作用不大。此外，随着桩-土剪切模量比增大，pk呈现逐步减小的趋势。这是由于模量比增大，土相对较软，Winkler弹簧刚度变小，导致扭矩变小。这说明在软弱地基中，土对桩的抗扭阻力将很小。

图6给出了 p2t随 H/r0和μ的变化。桩长细比H/r0增大，p2t逐渐减小，当长细比达到200左右时趋于稳定。这说明桩长增加到一定程度时，土的抗扭阻力 p2t不会再变化。同时，随着μ增大，p2t逐渐减小。这是由于土剪切强度越小，土越软弱，导致p2t越小。

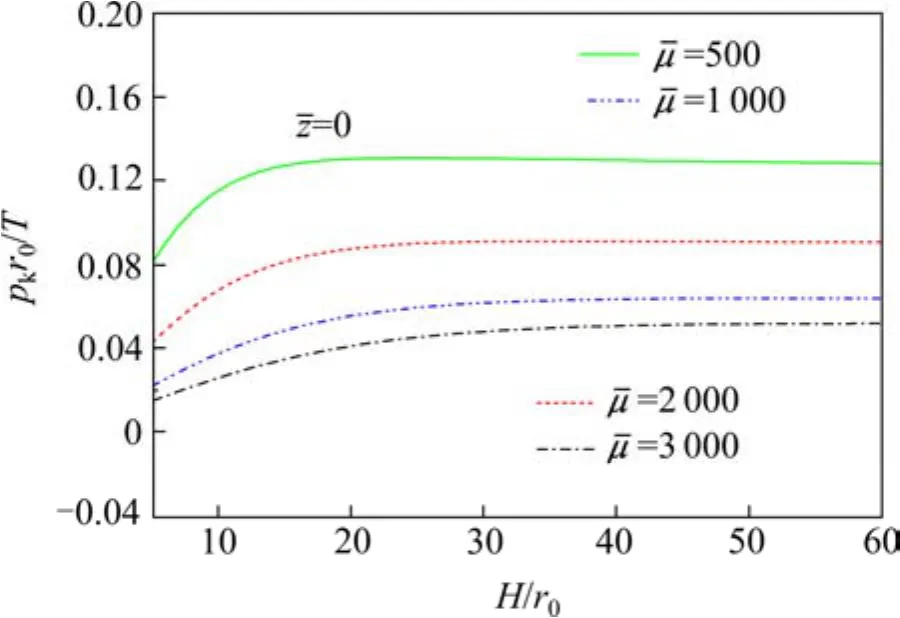
图5 不同剪切模量比下pk随长细比的变化Fig. 5 Variation of pk with the slenderness ratio for different shear modulus ratio

图6 不同剪切模量比下p2t随长细比的变化Fig. 6 Variation of p2t with the slenderness ratio for different shear modulus ratio

5 结论

1) 扭转阻力由2个部分组成，分别为pk项和p2t项。其中pk项由τrθ产生，用Winkler弹簧表示。p2t项由剪应力τzθ产生，用薄膜表示。

2) 扭矩的 2个组成部分中，pk项的贡献大于p2t项。这说明桩在静扭矩荷载作用下，由周围土体压缩产生的扭转阻力大于土连续性产生的扭转阻力。

3) 随着长细比H/r0增大，pk逐渐增大随后保持不变，p2t逐渐减小随后保持不变。

4) 随着桩-土相对剪切模量比的增大，pk和p2t都逐步减小。这说明土越软弱，扭转阻力越小。

参考文献：

[1] Stoll U W. Torque shear text on cylindrical friction piles[J]. Civil Engineering, 1972, 42(4): 63-4.

[2] Novak M, Grigg R F. Dynamic experiments with small pile foundations[J]. Canadian Geotechnical Journal, 1976,13(4): 372-85.

[3] KONG L G, ZHANG L M. Experimental study of interaction and coupling effects in pile groups subjected to torsion[J]. Canadian Geotechnical Journal, 2008, 45(7):1006-17.

[4] Tham L G, Cheung Y K, Lei Z X. Torsional dynamic analysis of single piles by time-domain BEM[J]. Journal of Sound ＆Vibration, 1994, 174(4): 505-19.

[5] ZHANG L M, Tsang C Y M. Three dimensional analysis of torsionally loaded large-diameter bored pile groups[C]// Proceedings of the Sixth International Conference on Tall Buildings, 2005, 6-8: 311-317.

[6] Militano G, Rajapakse R K N D. Dynamic response of a pile in a multi-layered soil to transient torsional and axial loading[J]. Géotechnique, 1999, 49(1): 91-109.

[7] Novak M, Sachs K. Torsional and coupled vibrations of embedded footings[J]. Earthquake Engineering &Structure Dynamics, 1973, 2(1): 11-33

[8] Novak M, Nogami T. Soil-pile interaction in horizontal vibration[J]. Earthquake Engineering & Structure Dynamics, 1977, 35(5): 263-81.

[9] Novak M, Howell J F. Torsional vibration of pile foundations[J]. Journal of Geotechnical Engineering Division ASCE, 1977, 103(GT4): 271-85.

[10] Misra A, Saggu R, Basu D, et al. Analysis of pile subjected to torsion in multi-layered soil[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(5): 475-492.

[11] WANG Kuihua, ZHANG Zhiqing. Dynamic torsional response of an end bearing pile in saturated poroelastic medium[J]. Computers and Geotechnics, 2008, 35(3):450-458.

[12] 张智卿, 王奎华, 靳建明. 轴对称横观各向同性土体中桩的扭转振动响应研究[J]. 振动工程学报, 2011, 24(1):60-66.

ZHANG Zhiqing, WANG Kuihua, JIN Jianming.Torsional vibration of pile embedded in axisymmetric transversely isotropic soil[J]. Journal of Vibration Engineering, 2011, 24(1): 60-66.

[13] 王海东, 尚守平, 童桦. 层状地基端承桩动力阻抗研究[J]. 地震工程与工程振动, 2007, 27(1): 171-176.

WANG Haidong, SHANG Shouping, TONG Hua.Research on torsional dynamic impedance of end-bearing pile in layered soils[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(1):171-176.

[14] 王国才, 丁翠红, 王哲. 层状地基中单桩扭转振动特性分析[J]. 计算力学学报, 2009, 26(5): 715-721.

WANG Guocai, DING Cuihong, WANG Zhe. Study on the torsional oscillations of single pile embedded in layered foundation[J]. Chinese Journal of Computational Mechanics, 2009, 26(5): 715-721.

[15] Anoyatis G, Mylonakis G. Dynamic Winkler modulus for axially loaded piles[J]. Géotechnique, 2012; 62(6): 521-536.