混合多端直流输电系统的损耗优化控制

陈 东, 许 冬， 韩民晓, 陈守军, 刘庆时， 贾东强

(1. 国网经济技术研究院有限公司， 北京市 102209； 2. 华北电力大学电气与电子工程学院， 北京市 102206； 3. 国网北京市电力公司， 北京市 100031)

0 引言

多端直流输电系统与点对点的两端直流输电相比，由于其含有多个换流站，在实现常规能源与新能源发电汇集、多区域电力馈入等方面有显著优势，并运行方式更为灵活可靠[1]。中国目前已建成有近20条常规直流输电工程及数个柔性直流输电工程，为发展直流骨干网络提供了坚实的技术积累。通过将常规直流和柔性直流各自的经济和技术优势互补，以发展中国的直流输电骨干网架，文献[1]提出了混合多端直流输电系统的初步规划。

针对常规多端直流输电系统，文献[2-3]研究了其功率调制技术，文献[4-6]研究了其故障特征及保护策略。虽然两端常规直流输电技术已十分成熟，然而由于常规多端直流输电系统的协调控制依赖通信、难以实现自律分散控制等原因，到目前为止全世界范围内仅有5个已建成的常规多端直流工程[7]。但模块化多电平拓扑出现以后，易于组网的基于电压源换流器(VSC)的高压直流输电技术迅速发展，各国建设了一系列用于异步联网及新能源电场并网的柔性直流输电工程，并且中国率先建成了南澳、舟山多端柔性直流输电工程[8]，此外还有张北柔性直流电网工程在稳步推进。然而，随着直流输电技术向着更多端子及网络化的方向发展，实现集中控制更为困难。而下垂控制由于其不依赖通信、各端子可自动协调分配功率的特点成为多端直流输电系统协调控制策略的可行方案之一，文献[9-10]研究了确定柔性多端直流输电系统下垂控制参数的方法；文献[11-12]分析了采用下垂控制时的直流潮流分布。虽然基于下垂控制的协调控制策略能实现系统的稳定运行，但无法保证系统工作在最优运行点，因此文献[13-16]研究了多端柔性直流输电系统满足特定目标函数的参考点设定方法。然而由于混合多端直流输电系统的运行呈现出一些新的特点，在实现损耗优化的同时必须考虑电网换相换流器(LCC)逆变站的最小熄弧角(γmin)限制，因此上述成果不能直接用于混合多端直流输电系统的损耗优化控制，必须重新设计符合混合多端直流运行特性的损耗优化控制策略。

因此，本文结合混合多端直流输电的特点，提出了损耗优化分层控制方案：底层为混合多端直流各端子的下垂控制，以实现对功率变化的快速调节；上层为优化控制，根据系统的输入功率，并结合系统的约束条件计算下垂控制参数，使系统达到最优运行状态。虽然优化控制需要各端子间的通信以获取全局信息，但损耗优化控制可在较长的周期或者在功率变化满足一定条件时进行，实际中用于监视和保护的通信系统速率已能满足要求[17]。

本文以一个混合六端直流输电系统为例验证了所提控制策略的损耗优化效果。首先根据优化算法计算了混合多端直流输电系统稳态时的优化结果，然后在PSCAD/EMTDC中对功率波动、通信故障情形下的控制策略有效性进行了仿真验证。

1 损耗优化控制

1.1 控制结构

若仅采用下垂控制，虽然不需要通信，但不能保证混合多端直流输电系统在任意输入功率下运行在最优工作点，因此本文为混合多端直流输电系统设计了如图1所示的损耗优化分层控制方案。其中，底层为混合多端直流输电系统各端子的下垂控制，以实现对功率变化的快速调节；上层为优化控制，根据系统的输入功率，并以损耗最小为目标优化底层下垂控制的参数，使系统达到最优运行状态。

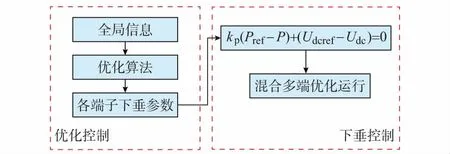
图1 端子分层控制方案示意图Fig.1 Herarchical control scheme of each terminal

由于送端换流站可能连接新能源电场或火电孤岛等，可认为其吸收送端电源的全部功率，不受上层指令的调节，从而受端换流站的控制是完成优化目标的关键。受端换流站根据上层调度指令选择不同的控制模式，若不参与混合多端直流输电系统的优化控制，则运行在定电压或定功率/电流控制模式；若参与优化控制，则受端换流站接收上层优化控制输出的结果，调节各自的下垂控制参数，使整个混合多端直流输电系统达到损耗最小的运行点。

本文提出的损耗优化控制策略对混合多端直流输电系统运行点的调节作用见附录A图A1。图中垂直于横轴的为送端换流站的运行曲线，斜线为受端换流站的下垂特性曲线。设O1为系统的初始运行点且处于损耗最小的最优运行状态，功率为P1，直流电压为Udc1。若某时刻开始系统功率开始下降，若没有损耗优化控制，则运行点将沿受端换流站的下垂特性曲线移动到O2点，直流电压降低，系统的损耗率升高。然而，在损耗优化控制的调节下，受端换流站的下垂特性将向上平移，系统的运行点将从O2点移动到O3点，直流电压升高，降低了系统损耗。

1.2 优化算法

为防止LCC逆变站发生换相失败，必须在实现系统损耗优化的同时满足其最小熄弧角的限制。然而，LCC逆变站若保持熄弧角不变将会呈现负阻抗特性，因此混合多端直流输电系统的损耗优化控制与多端柔性直流输电系统的控制相比有很大不同。本文选取混合多端直流输电系统的总损耗(线路损耗和换流站损耗)作为目标函数，则混合多端直流输电系统的优化算法为使损耗最小需要使直流电压尽可能高且功率尽量经LCC逆变站送出。但为了保证LCC逆变站不发生换相失败，需要在其流过较大电流时，相应地降低直流电压，以维持合适的熄弧角，即混合多端直流输电系统的损耗优化需要寻求最优的功率分配与直流电压组合。本文设计的混合多端直流损耗优化算法见图2。

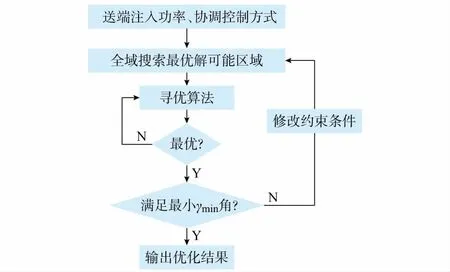
图2 各端子优化算法流程图Fig.2 Flow chart of optimization algorithms of each terminal

如图2所示，损耗优化算法首先根据送端的注入功率与系统的约束条件全域搜索最优解可能存在的范围，然后在可行域内应用寻优算法求取极值点，最后选取使目标函数值最小的极值点作为最优解，图中的寻优算法为内点法[18]。然而此时优化结果中LCC逆变站的电压和电流可能不满足最小熄弧角的限制，在输出最终结果之前需要先进行判断，若不满足则修改约束条件，增加LCC逆变站最小熄弧角的约束条件重新计算。

尽管上层优化控制需要通信以获得全局信息，但损耗优化控制可以在较长周期或者在功率变化满足一定条件时进行，实际中用于监视和保护的通信系统速率已能满足要求。若发生通信故障，则VSC端子降低下垂控制的电压参考值至一个较低的预设值，保证其在送端满功率运行时直流电压依然不超出上限，LCC逆变站也将暂时退出优化控制直到通信恢复。在通信故障和恢复的暂态过程中，各参考值都将以合适的速率变化以避免系统电气量出现过大峰值。

1.3 目标函数与约束条件

混合多端直流输电系统的损耗由线路损耗和换流站损耗组成，其中线路损耗Ploss1可表示为：

Ploss1=(IMU)TGDC(IMU)

(1)

式中：IM为关联矩阵；U为电压列向量；GDC为直流网络电导矩阵。

受端换流站损耗Ploss2可表示为[19]：

(2)

式中：Ploss,invi为逆变站损耗;s0，s1，s2分别为相应的损耗系数；Ith为流过换流站的电流。

不计送端换流站的损耗是因为其输入功率已经确定，因此损耗也已确定。则损耗优化的目标函数，即混合多端直流输电系统的总损耗率可表示为：

(3)

式中：Ploss，i为第i个受端换流站的损耗；Ei和Ii分别为送端换流站节点的电压和电流。

混合多端直流输电系统的约束条件包括直流网络各支路电流的上下限、各节点的电压上下限、各节点的注入功率限制及熄弧角限制。其中，直流网络各支路的电流限制为线性不等约束，即

Iij,min≤Iij≤Iij,max

(4)

式中：Iij,min和Iij,max分别为支路(i,j)电流的最小值和最大值；Iij为支路(i,j)的电流。

为便于计算，将式(4)改写为矩阵不等式形式。即

Ax≤b

(5)

式中：A和b的值见附录B;x等价为电压列向量U。

满足逆变侧LCC最小熄弧角限制时节点电压电流关系为线性等式约束，即

(6)

式中：U3为受端LCC的电压；Uac为LCC3交流侧线电压有效值；γ为LCC逆变站的熄弧角；Xr为换相电抗；Id为受端LCC的电流。

送端换流站的注入功率为非线性等式约束：

Pi=Ui∑YijUj

(7)

式中：Pi为送端换流站的注入功率；Ui和Uj分别为节点i，j的电压;Yij为节点i，j之间的导纳。

受端换流站的功率限制为非线性不等约束：

(8)

式中:Smax,i为第i个换流站视在功率最大值，Qi为第i个换流站的无功功率。

各换流器直流电压的上下限为上下限约束，即

0.95≤Ui≤1.05

(9)

2 稳态优化结果

2.1 混合六端直流输电系统

本文为验证损耗优化控制策略功能建立的混合六端直流输电系统如图3所示。

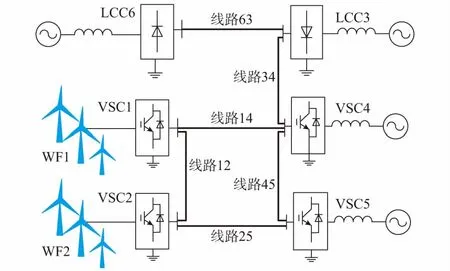
图3 混合六端直流输电系统示意图Fig.3 Schematic graph of six-terminal hybrid HVDC

图3中，VSC1和VSC2分别连接两个风电场WF1和WF2，并采用定交流电压定频率控制以吸收其发出的全部功率；LCC6连接交流系统，功率由电网调度决定;LCC3，VSC4，VSC5为3个受端换流站，是可参与损耗优化控制的端子。损耗优化算法正是通过对3个受端换流站的调节，实现了混合多端直流输电系统的最优运行。因此，损耗优化目标函数的变量为3个受端换流站的电压U3，U4，U5，受其影响的变量为3个送端换流站的电压U1，U2，U6。

2.2 优化算法的参数

本文首先选取图3所示的混合六端直流输电系统总损耗作为目标函数，并分析系统的约束条件，最后用图2所示的优化算法得出参与优化控制的VSC电压和功率参考值与LCC的电流参考值。以下的算例基于最复杂的情况，即LCC3,VSC4,VSC5都参与损耗优化控制模式，U3，U4，U5都为控制变量(LCC3的电流指令由电压结果算出)。其他情况由于算法类似，仅在最后提供结果以供比较分析。

因此，式(1)中的电压列向量为U=[U1,U2,U3,U4,U5]T，Ui为各节点直流电压，i为换流器标号。IM和电导矩阵GDC的值见附录B。

LCC3的直流电流可表示为：

Id=I63+I34=I63+G34(U4-U3)

(10)

式中：I63为线路63上流过的电流，即LCC6的电流指令；I34为线路34上流过的电流；G34为线路34的电导。

联立式(6)和式(10)可得式(5)形式的表达式为：

Aeqx=beq

(11)

其中，Aeq=[0，0，1，a，0]，a=6XrG34/(π-6XrG34)；beq=(2.7πUaccosγ-6XrI63)/(π-6XrG34)。

综上，图3中混合六端直流输电系统约束条件如式(5)至式(11)所示，其中式(11)为满足LCC3最小熄弧角限制的约束条件。

2.3 稳态优化结果

图3所示的混合六端直流输电系统参数见附录A表A1，给出了与损耗优化有关的功率、电压等关键参数。与损耗有关的直流线路电阻参数见附录A表A2。

本文通过在MATLAB中编程得到了优化算法的稳态优化结果，如附录A表A3所示，比较了3种情形下的下垂控制参数与混合多端直流输电系统的损耗。第1种情形为只有一个端子(VSC5)参与优化控制且LCC3的电流指令与LCC6相同，其余端子采用定功率/电流控制；第2种情形为有两个端子(LCC3和VSC5)参与优化控制，另一个端子(VSC4)采用定功率控制；第3种情形为受端3个端子(LCC3,VSC4,VSC5)都参与优化控制。3种情形中，WF1发出的功率为150 MW，WF2发出的功率为200 MW，LCC6的电流指令为1.6 kA，VSC4和VSC5功率因数都为1。

从附录A表A3可以看出，在系统输入功率一定的情况下随着参与优化控制的换流器增多，系统的损耗逐渐降低。情形1中，只有VSC5在损耗优化控制作用下调节本节点的电压来降低系统损耗，由于LCC3与LCC6的电流指令相同，没有承担风电场发出的功率，LCC3的电流是3种情形中最小的，所以其直流电压是比其余2种情形大。情形2中，LCC3承担了一部分风电场发出的功率，虽然在损耗优化算法的作用下将直流电压变低，但由于LCC的损耗率比VSC小，所以系统总体损耗率降低。情形3中，3个换流器均参与损耗优化控制，损耗优化控制算法协调各换流站的功率分配与直流电压，使功率更多地从LCC3流出，即使直流电压进一步降低，但损耗率却是3种情形中最低的。

考虑到LCC3须满足最小熄弧角的限制条件，系统直流电压在LCC3流过的电流较大时需要降低。附录A表A4中，比较了2种情形下优化后的下垂参数，3个换流器均参与优化控制。情形1中，LCC6的直流电流为1 kA，WF1和WF2的输出功率均为150 MW。情形2中，WF1和WF2的输出功率分别增加到200 MW和250 MW，LCC6的直流电流为1.6 kA。可以看出在功率较低时，由于LCC3的熄弧角大于其最小值，直流电压较高；在功率较大时，为满足LCC3最小熄弧角的限制，直流电压处于较低水平，损耗率也有所增加。

3 仿真验证

虽然上述稳态优化结果计算表明各端子采用的优化控制能够起到降低系统损耗的作用，但仍需对损耗优化控制在功率变化及通信故障时的控制效果进行仿真验证。

本文仿真了最复杂的情形，即3个受端换流站都参与优化控制。其中两个VSC换流站的V-I特性为：

kp(Pref-P)+Udc，ref-Udc=0

(12)

式中：kp=-0.166 7；Pref为功率指令，上下限分别为300 MW和0；P为换流站功率实测值；Udc为换流站直流电压；Udc，ref为电压指令，上下限分别为525 kV和475 kV。

LCC3的V-I特性为：

I=Iref

(13)

式中：I为直流电流；Iref为直流电流参考值。

端子各自计算其下垂或电流参考值，计算周期为0.1 s，即每隔0.1 s优化一次其参考值。实际中功率变化较为缓慢，控制周期可以更长，这里只是节省仿真时间设置了较短的控制周期和较快的功率变化率。仿真的情形与对应时刻见附录A表A5。

令LCC和VSC的基准功率分别为1 000 MW和300 MW，以流入直流网络的功率为正。混合六端直流输电系统在2 s时进入稳定运行，风电场功率均为0.5(标幺值)，LCC6的电流为0.5(标幺值)。图4为各端子的功率，可以看出，此时LCC3承担了风电场(WF1和WF2)发出的大部分功率，VSC5只承担了少量的功率。t=3 s时，WF1的功率增加到200 MW；t=4 s时，WF2的功率增加到250 MW，损耗优化控制算法协调3个受端换流站合理分配风电场增加的功率。图5为各端子的直流电压，基准值为500 kV。在2～5 s这段时间内，由于LCC3承担的功率较少，LCC3的熄弧角大于其最小值，无需进一步降低直流电压，损耗率也较低。LCC6的电流在5 s时增加到0.8，此时LCC3的电流在损耗优化控制算法的调节下接近1.0(标幺值)，但同时损耗优化算法也进一步降低VSC的直流电压参考值，并使VSC4和VSC5承担了更多功率，避免了换相失败的发生，但损耗率也升高至1.51%。t=6 s时，混合多端直流通信故障，损耗优化控制将VSC的下垂控制的电压与功率参考值切换到预先设定的值，此预先设定的值以在最大功率时电压不越限且不发生换相失败为原则进行计算，这里分别设定为300 MW和500 kV，LCC3不再参与优化控制，电流指令变为与LCC6相同，此时，不仅直流电压进一步降低而且受端VSC4和VSC5承担了风电场发出的全部功率，导致损耗率升高至1.64%。t=7 s时通信恢复，换流站又可根据接收的送端换流站功率信息进行优化控制，因此，损耗率重新降为1.51%。

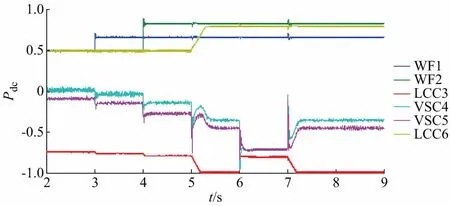
图4 换流站功率Fig.4 Power flow of each converter

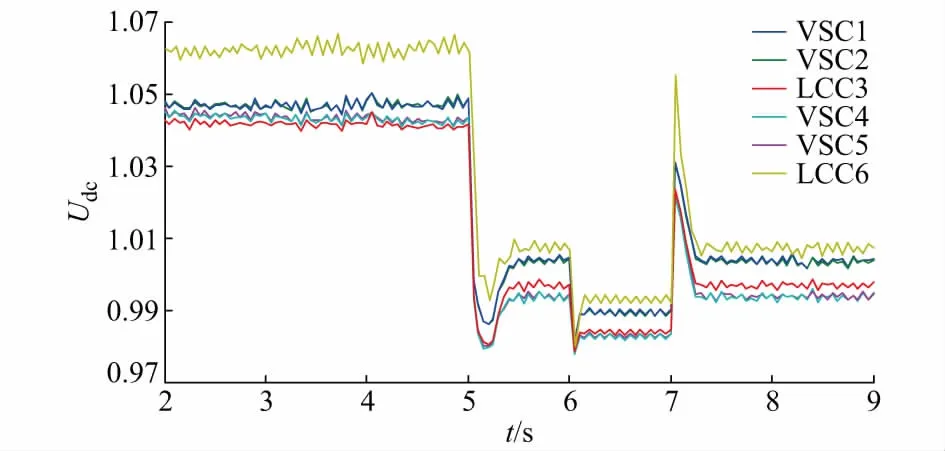
图5 直流电压Fig.5 DC voltage of each converter

从图4和图5可以看出，损耗优化控制可及时在送端换流站注入功率变化时调整功率在受端3个换流站的分配与直流电压参考值，在保证整个混合多端直流输电系统损耗最小的同时确保LCC3不发生换相失败，因此本文提出的损耗优化控制适合应用在混合多端直流输电系统中。从图6可看出，仿真得出的系统损耗与理论计算得出的稳态值基本吻合，说明本文的损耗优化算法准确，从6～7 s这段时间可以看出，功率自然分布时，系统的损耗将显著增大，说明本文的优化算法起到了降低损耗的效果。

4 结语

为解决下垂控制不能保证混合多端直流输电最优运行的局限，本文提出了损耗优化控制策略，该控制策略能在满足LCC逆变站熄弧角限制条件的前提下，有效降低混合多端直流输电系统总体损耗率。

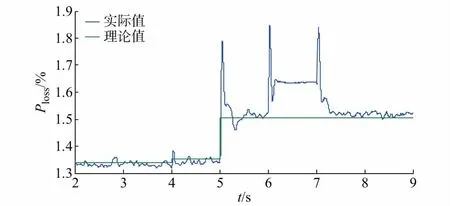
图6 系统损耗率Fig.6 Loss rate of system

稳态优化计算结果表明,参与优化控制的端子越多,系统损耗越小，并且优化控制算法能在注入功率较大时降低直流电压，达到防止LCC逆变站换相失败的目的。随后的仿真验证表明，损耗优化控制策略能够协调控制混合多端各端子达到预定的优化目标，符合理论计算结果，并在功率波动、通信故障情形下能够及时控制各端子的电压和功率，有着良好的控制效果。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 袁旭峰.新型混合多端直流输电系统理论及其若干关键问题研究[D].武汉:华中科技大学,2007.

[2] 袁旭峰,文劲宇,程时杰.多端直流输电系统中的直流功率调制技术[J].电网技术,2007,31(14):57-61.

YUAN Xufeng, WEN Jinyu, CHENG Shijie. DC power modulation in multi-terminal HVDC transmission system[J]. Power System Technology, 2007, 31(14): 57-61.

[3] 许丹,姜曼,郑晓雨,等.含多端柔性直流电网的调度计划优化建模[J].电力系统自动化,2017,41(23):22-28.DOI:10.7500/AEPS20170217003.

XU Dan, JIANG Man, ZHENG Xiaoyu, et al. Optimal modeling of dispatch scheduling for power grid with VSC-MTDC system[J]. Automation of Electric Power Systems, 2017, 41(23): 22-28. DOI: 10.7500/AEPS20170217003.

[4] 徐政,胡永瑞,傅闯.并联型多端直流输电系统的控制策略与故障特征[J].高电压技术,2013,39(11):2721-2729.

XU Zheng, HU Yongrui, FU Chuang. Control strategy and fault characteristic of parallel MTDC transmission systems[J]. High Voltage Engineering, 2013, 39(11): 2721-2729.

[5] 王俊生,吴林平,郑玉平.多端高压直流输电系统保护动作策略[J].电力系统自动化,2012,36(10):102-123.

WANG Junsheng, WU Linping, ZHENG Yuping. Protection action strategy of multi-terminal HVDC transmission system[J]. Automation of Electric Power Systems, 2012, 36(10): 102-123.

[6] 许烽,徐政,傅闯.多端直流输电系统直流侧故障的控制保护策略[J].电力系统自动化,2012,36(6):74-78.

XU Feng, XU Zheng, FU Chuang. Control and protection strategy of DC fault in multi-terminal HVDC system[J]. Automation of Electric Power Systems， 2012, 36(6): 74-78.

[7] 汤广福,罗湘,魏晓光.多端直流输电与直流电网技术[J].中国电机工程学报,2013,33(10):8-17.

TANG Guangfu, LUO Xiang, WEI Xiaoguang. Multi-terminal HVDC and DC-grid technology[J]. Proceedings of the CSEE, 2013, 33(10): 8-17.

[8] 和敬涵,李智诚,王小君,等.计及换流器损耗与电压下垂控制的交直流系统最优潮流算法[J].电力系统自动化,2017,41(22):48-55.DOI:10.7500/AEPS20161231001.

HE Jinghan, LI Zhicheng, WANG Xiaojun, et al. Optimal power flow algorithm for hybrid AC/DC power systems considering power loss of converter and voltage-droop control[J]. Automation of Electric Power Systems, 2017, 41(22): 48-55. DOI: 10.7500/AEPS20161231001.

[9] AGUSTI E A, FEMANDO B, ADRIA J F, et al. Voltage control of multi-terminal VSC-HVDC transmission systems for offshore wind power plants: design and implementation in a scaled platform[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2381-2391.

[10] BIANCHI F D, ORIOL G B. Droop control design for multi-terminal VSC-HVDC grids based on LMI optimization[C]// Decision and Control and European Control Conference (CDC-ECC), December 12-15, 2011, Orlando, USA: 4823-4828.

[11] BEERTEN J, BELMANS R. Analysis of power sharing and voltage deviations in droop-controlled DC grids[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4588-4597.

[12] WANG W, BAMES M. Power flow algorithms for multi-terminal VSC-HVDC with droop control[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1721-1730.

[13] RODRIGO T P, PAVOL B, SILVIO F, et al. A novel distributed direct-voltage control strategy for grid integration of offshore wind energy systems through MTDC network[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2429-2441.

[14] MONICA A P, AGUSTI E A, ORIOL G B, et al. Optimum voltage control for loss minimization in HVDC multi-terminal transmission systems for large offshore wind farms[J]. Electric Power Systems Research, 2012, 89(1): 54-63.

[15] MONICA A P, AGUSTI E A, SAMUEL G A, et al. Droop control for loss minimization in HVDC multi-terminal transmission systems for large offshore wind farms[J]. Electric Power Systems Research, 2014, 112: 48-55.

[16] 许冬.混合多端直流输电运行特性研究[D].北京：华北电力大学,2017.

[17] XIAO L, BOYD S. Fast linear iterations for distributed averaging[C]// 42nd IEEE Conference on Decision and Control, December 9-12, 2003, Maui, USA.

[18] 韩民晓,许冬,万磊.基于一致性算法的混合多端直流自律分散控制[J].电力系统自动化,2016,40(12):130-136.DOI:10.7500/AEPS20150612001.

HAN Minxiao, XU Dong, WAN Lei. Consensus algorithm based decentralized autonomous control of hybrid multi-terminal direct current system[J]. Automation of Electric Power Systems, 2016, 40(12): 130-136. DOI: 10.7500/AEPS20150612001.

[19] BEERTEN J, COLE S, BELMANS R. A sequential AC/DC power flow algorithm for networks containing multi-terminal VSC HVDC systems[C]// IEEE Power and Energy Society General Meeting, July 25-29, 2010, Providence, USA: 1-7.