光伏电站暂态模型及其试验验证

曲立楠, 葛路明, 朱凌志, 牛拴保, 张 爽, 包斯嘉

(1. 中国电力科学研究院有限公司(南京), 江苏省南京市 210003; 2. 新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司), 北京市 100192; 3. 西北电网有限公司, 陕西省西安市 710000; 4. 国网宁夏电力有限公司, 宁夏回族自治区银川市 750000)

0 引言

随着光伏发电渗透率的不断提高,光伏发电对电力系统的影响越来越显著。大规模光伏电站接入电网后,光伏发电本身所特有的季节、昼夜的功率输出波动性给电网的安全稳定运行带来了新的挑战,包括对电网频率稳定、电压稳定、功角稳定等方面的影响。准确的光伏电站模型是开展并网分析的基础,具有显著的实际应用价值。

光伏电站接入电网的暂态仿真模型按照仿真步长划分可分为机电暂态模型和电磁暂态模型。电磁暂态模型可体现光伏电站内并网逆变器的脉宽调制(PWM)控制、电力电子开关状态等微秒级暂态特性[1];在电磁暂态模型的基础上,机电暂态进行了一定程度的简化,致力于实现在机电暂态时间尺度上准确描述光伏电站的暂态特性。由电磁暂态模型简化到机电暂态模型过程中,最大的跨度是忽略并网逆变器的电力电子开关动作和PWM控制,而更关注于影响光伏电站和并网逆变器并网性能的控制系统[2-4]。

早期,光伏电站暂态模型的研究成果多以风电场数学模型为基础,如2010年通用电气(GE)公司针对自己建设的光伏电站建立了暂态模型,该模型侧重光伏电站的无功控制,具有较强针对性[2]。2012年,美国西部电力系统协调委员会(WECC)发布了光伏电站通用模型结构,在GE模型的基础上增加了光伏发电参与系统有功调频控制模块,对光伏电站的有功和无功控制进行了改进[3],文献[5]利用电站控制系统向逆变器下达无功控制指令的实测数据验证了逆变器在该工况下的模型准确性。2014年国际大电网会议(CIGRE)和国际供电会议(CIRED)成立联合工作组C4/C6.35,致力于光伏、储能等电力电子设备的并网系统暂态模型研究,尚未发布成果。2016年,中国标准GB/T 32826—2016《光伏发电系统建模导则》提出了适用于国内光伏逆变器的通用化模型结构[4]。文献[6]参考德国标准FGW-TG4[7],分析光伏逆变器模型验证流程并给出实例。

上述研究成果或侧重于光伏电站控制系统模型结构,或基于单台逆变器实测数据开展部分模型验证,尚未实现整站模型验证及参数校核。本文根据光伏电站物理结构,提出了适用于机电暂态分析的光伏电站暂态模型,依据相关标准给出模型验证的流程与方法,并结合西北某省级电网光伏电站人工短路试验的实测数据,逐级验证了并网逆变器模型和光伏电站等值模型的有效性,分析了建模与模型验证过程中的关键技术因素,对所提模型的适用范围及其进一步完善和发展的方向进行了探讨。

1 光伏电站暂态模型

典型光伏电站拓扑结构采用多逆变器组合箱变为发电单元和多发电单元并联的形式,见附录A图A1。其中,一个光伏发电单元包含一台变压器和若干台逆变器,比如包含1至4台集中式逆变器或包含数十台组串式逆变器,每台逆变器单独与厂站级控制系统通信。光伏电站模型框架如图1所示,主要包括光伏方阵模型、光伏逆变器群模型、厂站级控制模型、集电线路和变压器模型。图1中:S为辐照度;Pm为当前辐照度下光伏方阵的最大功率；PPOI,ref和QPOI,ref分别为光伏电站并网点有功功率和无功功率参考值；PPOI和QPOI分别为光伏电站并网点有功功率和无功功率；Uterm为光伏逆变器交流侧电压基波正序分量。

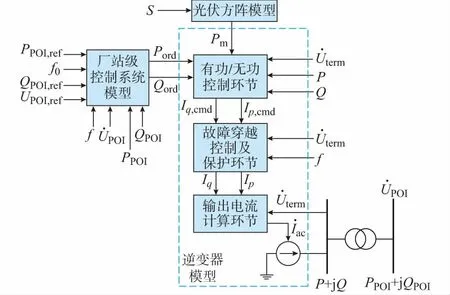
图1 光伏电站模型框架Fig.1 Framework of model for photovoltaic power plant

光伏方阵模型用于模拟环境变化对光伏方阵功率特性的影响,在机电暂态仿真中可以认为影响因素是辐照度。厂站级控制模型描述了在文献[8]要求的电压、频率稳定运行区域内光伏电站的有功功率/频率和无功功率/电压控制特性[9],属于电力系统动态稳定范畴[10],受篇幅所限本文暂不详述。光伏逆变器由电力电子元件构成,具有快速响应特性,在机电暂态过程中可以考虑为无延时响应。光伏逆变器等值模型用于描述光伏电站内所有逆变器集总的暂态特性,体现在接收并执行厂站级控制系统的控制指令、模拟光伏逆变器的故障穿越能力和保护特性。本文逆变器模型包括:有功/无功控制、故障穿越控制及保护、输出电流计算环节等。

1)有功/无功控制模型

有功/无功控制模型如图2所示,输入信号包括功率控制目标Pord和Qord、光伏方阵最大出力Pm和逆变器的实际输出功率P和Q,输出信号Ip，cmd和Iq，cmd分别表示有功、无功电流目标值。

图2中,Tp,ord为响应时间,取值范围为0.1～2 s;dPord,max和dPord,min分别为有功功率变化率上下限,取值范围分别为3～99(标幺值)和-99～-3(标幺值);dQord,max和dQord,min分别为无功功率变化率上下限,取值无限制;Tm为描述逆变器信号采样延迟的一阶惯性环节时间常数,取值范围为0.01～0.02 s;Kp和Tp为有功轴比例—积分(PI)控制器参数,Kq和Tq为无功轴PI控制器参数。根据逆变器的控制速度,Tp和Tq取值范围为0.02～0.5 s,Kp和Kq则取值范围较宽。其数学模型如式(1)所示。

(1)

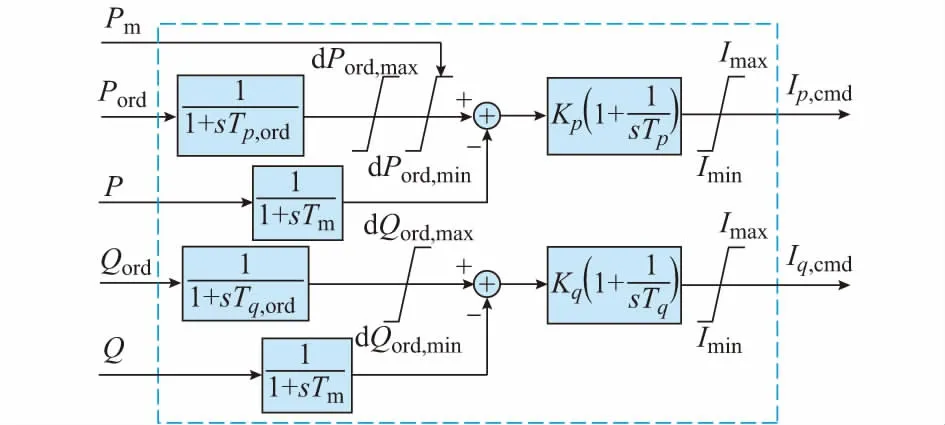
图2 有功/无功控制模块Fig.2 Active and reactive power control module

2)故障穿越控制及保护模型

故障穿越控制及保护模型如图3所示,输入信号包括逆变器交流电压基波正序分量Uterm、有功/无功控制模型输出的电流目标值Ip,cmd和Iq,cmd;输出信号Ip和Iq分别表示有功、无功电流。

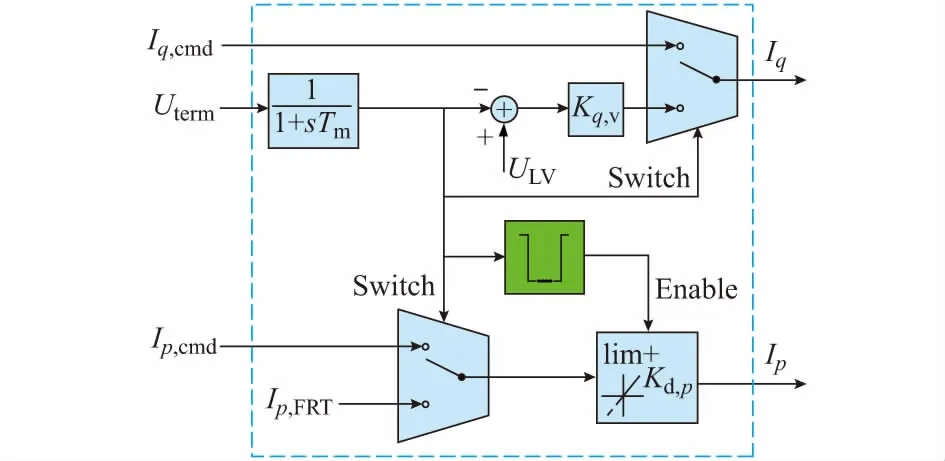
图3 组串型逆变器低电压穿越控制模块Fig.3 Low voltage ride-through control module of string inverter

图3中,ULV为逆变器低电压穿越的阈值电压,取值0.9(标幺值)[8];Kd，p为故障清除后有功电流恢复斜率,取值范围为0.1～10。Switch表示判断逆变器是否选择前级电流控制指令或是故障期间的电流指令,当低于ULV时,进入低电压穿越模式,Ip和Iq选择低电压穿越信号,否则选择前级有功/无功控制模块的电流控制指令Ip,cmd和Iq,cmd;绿色框表示判断逆变器交流侧电压是否恢复,而使能(Enable)有功电流上升速率限制环节(lim+)。数学模型如式(2)和式(3)所示。

(2)

Ip(t)=Ip(t-Δt)+Kd,pΔt

(3)

式中:Kq,LV为低电压穿越期间逆变器无功电流支撑系数,取值大于1.5[8];Ip,LV为低电压穿越期间逆变器有功电流参考值;t为仿真时间;Δt为仿真步长。

3)输出接口环节

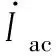
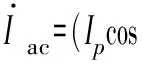
(4)

式中:θ为逆变器交流侧电压相角。

2 模型验证方法

本文所述光伏电站模型适用于电力系统机电暂态仿真分析,如DIgSILENT PowerFactory,PSASP,PSS/E等仿真工具,因此模型验证的工况为光伏电站机电暂态仿真时间尺度的运行工况。当电网发生大扰动故障时,记录光伏电站三相瞬时数据,通过提取试验数据的基波正序分量,包括光伏电站的电压、电流、有功功率、无功功率等电气量，设置与试验相同场景的仿真工况,通过仿真与试验测试数据对比,验证模型和参数的准确性。

2.1 模型验证流程

光伏电站的模型验证流程如图4所示。

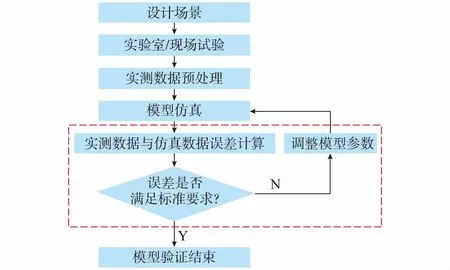
图4 模型验证流程Fig.4 Flow chart of model validation

首先,分析光伏电站暂态特性的主要影响因素,设计试验场景;在现场或实验室开展测试,记录试验数据,三相瞬时数据采样率不小于1 kHz;提取各电气量的基波正序分量,数据预处理结果与仿真步长保持一致,取1～10 ms;模型仿真,设置与试验相同的场景,并根据仿真与试验数据的误差调整模型参数,直至误差计算满足模型评价标准。

为保证模型验证和参数辨识的通用性,模型验证的场景设计需充分考虑光伏电站与电网交互影响的主要特征,如电网发生对称或不对称短路故障,电网丢失大负荷或电源造成频率扰动等。由于模型验证场景多元化,光伏电站的模型参数需适用于不同的试验场景。

初始参数辨识利用分工况试验数据开展,具体为有功/无功控制试验、辐照度扰动试验和光伏逆变器交流侧小扰动试验用于调整有功/无功控制模型参数;电网单相短路故障、三相短路故障等试验用于调整故障穿越控制及保护模型参数;厂站级控制模型参数辨识试验主要涉及调度指令、电压/频率波动等。

需要强调的是,一组试验数据辨识参数的结果只能满足单一工况的模型验证,本文采用多工况迭代的参数辨识方法,不断调整参数使得一组参数满足全部试验工况的模型验证技术要求。

2.2 模型评价标准

基于电力系统仿真工具,建立光伏电站数学模型,设置与试验相同的仿真场景,如电网发生短路故障,导致光伏电站并网点电压跌落,恢复至新稳态。

模型验证过程中,用于对比的仿真与测试数据包括光伏电站并网点电压、电流、有功功率、无功功率和无功电流[14],以电压为依据,将测试与仿真的数据序列分为A(故障前)、B(故障期间)、C(故障后)3个时段;以各变量暂态特性为依据,将B,C时段分为暂态区间和稳态区间,其中B时段分为B1(暂态)和B2(稳态)区间,C时段分为C1(暂态)、C2(稳态)区间。各时段中用于评判模型与参数优劣的误差类型及计算方法如表1所示。

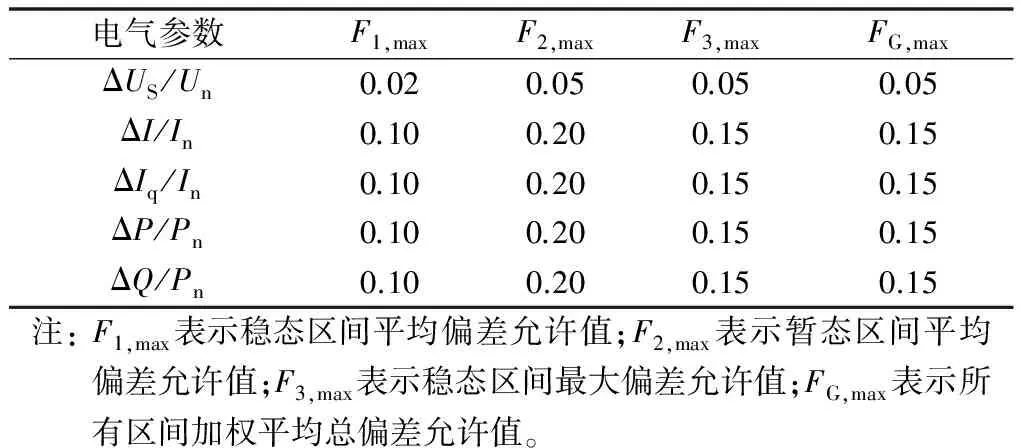
表1 模型验证允许最大偏差值Table 1 Allowed maximum error for model validation

表1中,各电气量的稳(暂)态区间平均偏差F1(2)计算如下:

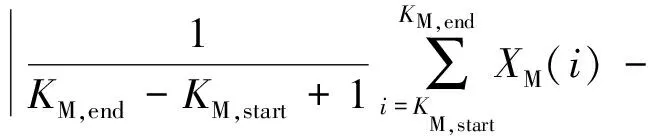
(5)

式中：KM,start,KS,start,KM,end,KS,end分别表示相应区间的测试和仿真第一个和最后一个数据的序号;XM和XS分别表示表1中电气量的测试和仿真数据的标幺值。

稳态区间最大偏差F3为:

(6)

加权平均总偏差FG为:

FG=0.1FA+0.6FB+0.3FC

(7)

式中:FA,FB,FC分别为A,B,C时段测试和仿真数据的平均偏差。

3 光伏电站模型验证算例

本文借助输电线路人工短路试验契机,监测并记录并网光伏电站的暂态特性,完成光伏电站暂态模型的逐级验证。

3.1 试验场景

西北某省级电网750 kV输电线路人工短路试验,单相接地,短路点附近有大规模光伏发电站群高压接入,见附录B图B1。被测光伏电站接入电压等级35 kV,靠近短路试验点,当前入网额定容量为6.9 MW,由191台36 kW组串式逆变器组成,经35 kV母线并入电网;电站内,共4个发电单元串联连接,每个发电单元由9条并联支路和单元升压变压器组成;每条并联支路为6台组串式逆变器并联。试验中,监测光伏电站A的并网点和1号单元的1号逆变器。

经短路试验实测数据分析,电站并网点电压跌落用时0.02 s,最大跌落深度0.858(标幺值),无功电流输出最大为0.06(标幺值),有功电流输出最小为0.253(标幺值)。1号单元的1号逆变器交流侧电压跌落用时0.02 s,最低跌落深度为0.859(标幺值),无功电流输出最大值为0.085(标幺值),有功电流输出最小值为0.02(标幺值)。

3.2 模型验证算例

按照本文2.1节所述的模型验证流程,首先,设计仿真场景与本文3.1节所述试验相吻合:建立光伏电站等值模型,包括光伏逆变器等值、电站集电升压系统等值模型;通过两级升压系统,建立等值外网模型,根据电站接入点短路比的实际情况,设置等值外网的容量及阻抗。其次,处理实验录波数据,包括光伏电站并网点、光伏发电单元箱变高压侧、逆变器机端3个测量点数据,提取电气量的基波正序分量,降低实测数据采样率至电网暂态分析计算的通用步长(本文为10 ms)。之后,开始模型仿真和参数辨识,并利用3组数据反复优化式(2)和式(3)的主导参数,辨识结果如下：ULV=0.9(标幺值),Kq,LV=3.6,Kd,p=1.25。最后,模型验证,按照本文2.2节进行区间划分和误差计算,模型验证结果如图5和附录C图C1所示,对应的误差计算结果见附录C表C1和表C2,其中各参数均为标幺值。

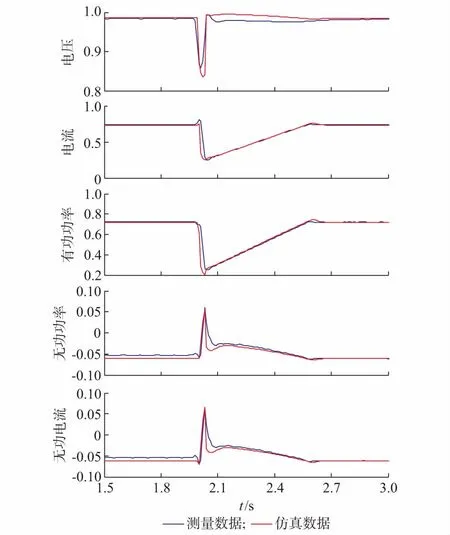
图5 光伏电站模型验证Fig.5 Model validation of photovoltaic power plant

试验中,光伏逆变器机端电压最大跌落深度低于0.9(标幺值),进入低电压穿越状态,其暂态特性仿真通过控制模型的故障穿越控制模块策略切换实现,准确地模拟了逆变器低电压穿越过程中无功电流支撑及低电压穿越结束后的有功功率恢复过程。

相对于单台逆变器的模型验证,光伏电站的模型验证工作更难,本文采用2台等值逆变器模拟整站,后文3.3节详细描述了原因。由图5对比结果可见,光伏电站等值模型准确模拟了包含191台逆变器的光伏电站低电压穿越暂态过程,可用于光伏电站接入电力系统分析计算。

3.3 模型验证结果分析

结合大电网人工短路试验,监控光伏电站暂态特性,由模型验证的结果可得出如下结论。

1)逆变器等值模型可准确描述光伏电站内所有逆变器集总的暂态特性。

被监测光伏电站采用同一型号光伏逆变器,且逆变器电气距离接近,可近似认为逆变器机端电压无显著差异。然而，对比逆变器和整站暂态特性可知,光伏电站并网点与逆变器机端电压跌落深度近乎一致,而两者在故障穿越期间的有功功率和无功功率均不相同。

试验前后,调取光伏电站运行数据,正常运行时光伏发电单元1,2,4的各逆变器交流侧电压为470 V左右,而光伏发电单元3的各逆变器交流侧电压为496 V左右。由此判断,当电站并网点电压跌落至0.858(标幺值)时,光伏发电单元1,2,4的各逆变器交流侧电压跌落至0.859(标幺值),逆变器进入低电压穿越运行状态;而光伏发电单元3的各逆变器交流侧电压仍高于0.90(标幺值),逆变器未进入低电压穿越运行状态。因此,上节中建立了2台等值逆变器模型,完成模型验证。

光伏电站内逆变器运行状态不一致的情况增加了等值建模的复杂度。

2)模型仿真不可避免地存在着与实际系统暂态特性的偏差。

仔细观察实测短路试验瞬间光伏电站并网点电压、电流、有功功率和无功功率(见附录D图D1)。试验时间1.98 s时并网电压开始跌落,2.01 s跌落至最低点,2.04 s恢复至故障前状态;与此同时,2.01 s光伏电站的无功电流支撑才起作用,滞后电网电压0.02 s;同样的,光伏电站的有功电流也相应延迟动作。

在模型仿真中,仿真程序会在事件(本文指短路故障)开始和结束时刻变步长处理,如在t1时刻设置事件发生,则处理为t1+和t1-,从而导致电压跌落瞬间完成。本文所提模型借助图2、图3中设置的信号采样延时环节(Tm)减缓模拟该过程的偏差。

此外,研究图5的全过程录波曲线,在实际运行中,若电网中的光伏发电渗透率较高,则无功支撑的偏差以及故障后的有功缺额将会造成严重后果。后续将进一步研究高渗透率光伏发电对电力系统稳定性的影响并加以改进。

4 结语

基于典型光伏电站的结构,本文论述了影响光伏电站并网性能的主要因素,构建了一种用于电力系统暂态仿真的光伏电站数学模型,该模型考虑了厂站级控制系统模型、描述站内逆变器集总特性的逆变器等值模型,其中逆变器模型包括有功/无功控制模块、故障穿越控制及保护模块、并网接口模块。

进一步提出了一种应用多工况实测数据验证光伏电站数学模型有效性的方法。该方法强调一组光伏电站数学模型及参数能够准确描述不同场景下的光伏电站暂态特性,且仿真与实测数据误差满足相关标准的技术要求。

应用西北某省级电网750 kV输电线路人工短路试验的光伏电站监测数据,验证了本文提出的光伏电站模型的准确性和模型验证方法的有效性。基于大量光伏逆变器实验室测试数据,借助人工短路试验监测数据,开展光伏电站模型实测及验证,进一步论证了逆变器实验室实测模型与光伏电站详细模型、等值模型的关联性。

本文所提光伏电站数学模型为包含大规模光伏发电的电力系统安全稳定分析和运行控制提供了基础模型和数据支撑,可广泛应用于方式计算、运行规划、事故分析及反措制定等方面,具有实际应用价值。基于实测数据,还将进一步开展光伏电站暂态特性对区域电网消纳光伏发电的量化分析。

本项目同时由中国电力科学研究院创新基金“光伏发电跨平台统一建模技术与实现”资助，谨此致谢！

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 许寅,陈颖,陈来军,等.基于平均化理论的PWM变流器电磁暂态快速仿真方法:(一)PWM变流器分段平均模型的建立[J].电力系统自动化,2013,37(11):58-64.

XU Yin, CHEN Ying, CHEN Laijun, et al. Fast electromagnetic transient simulation method for PWM converters based on averaging theory: Part one establishment of piecewise averaged model for PWM converters[J]. Automation of Electric Power Systems, 2013, 37(11): 58-64.

[2] CLARK K, MILLER N W, WALLING R. Modeling of GE solar photovoltaic plants for grid studies[R]. Boston, USA: General Electric International Inc., 2010.

[3] WECC Renewable Energy Modeling Task Force. Generic solar photovoltaic system dynamic simulation model specification[R]. 2012.

[4] 光伏发电系统建模导则:GB/T 32826—2016[S].北京:国家标准化出版社,2016.

[5] MORJARIA M, ANICHKOV D, CHADLIEV V, et al. A grid-friendly plant: the role of utility-scale photovoltaic plants in grid stability and reliability[J]. IEEE Power & Energy Magazine, 2014, 12(3): 87-95.

[6] 刘美茵,黄晶生,张军军,等.基于BDEW标准的光伏并网逆变器模型验证及误差分析[J].电力系统自动化,2014,38(13):196-201.DOI:10.7500/AEPS20130922004.

LIU Meiyin, HUANG Jingsheng, ZHANG Junjun, et al. Model validation and error analysis of photovoltaic grid-connected inverter based on BDEW standard[J]. Automation of Electric Power Systems, 2014, 38(13): 196-201. DOI: 10.7500/AEPS20130922004.

[7] FGW. Technical guidelines for power generating units: Part 4 demands on modeling and validating simulation models of the electrical characteristics of power generating units and systems[S]. 2010.

[8] 光伏发电站接入电力系统技术规定:GB/T 19964—2012[S].北京:中国电力出版社,2012.

[9] QU Linan, ZHU Lingzhi, GE Luming, et al. Research on multi-time scale modelling of photovoltaic power plant[C]// 4th IET International Conference on Renewable Power Generation (RPG), October 17-18, 2015, Beijing, China: 5p.

[10] 电力系统安全稳定导则:DL 755—2001[S].北京:中国电力出版社,2001.

[11] 辛凯,刘云峰,郭海滨.逆变器及PWM调制方法:201310330391.9[P].2013-07-31.

[12] 张兴,曹仁贤.太阳能光伏并网发电及其逆变控制[M].北京:机械工业出版社,2011.

[13] 张磊,朱凌志,陈宁,等.新能源发电模型统一化研究[J].电力系统自动化,2015,39(24):129-138.DOI:10.7500/AEPS20150629010.

ZHANG Lei, ZHU Lingzhi, CHEN Ning, et al. Review on generic model for renewable energy generation[J]. Automation of Electric Power Systems, 2015, 39(24): 129-138. DOI: 10.7500/AEPS20150629010.

[14] 光伏发电系统模型及参数测试规程:GB/T 32892—2016[S].北京:中国电力出版社,2016.