湖南电网山火告警风险及故障时间间隔分布规律
2018-05-23周特军陆佳政吴传平
周特军, 陆佳政, 吴传平, 李 波, 刘 毓
(1. 电网输变电设备防灾减灾国家重点实验室(国网湖南省电力有限公司), 湖南省长沙市 410007;2. 国网湖南省电力有限公司防灾减灾中心, 湖南省长沙市 410007)
0 引言
电网停电事故严重威胁经济的发展和社会的稳定。然而,电网大停电事故时有发生[1-2],如2003年美加大停电、2006年西欧大停电、2008年中国南方特大冰灾导致湖南电网解列、2012年印度大停电、2017年中国台湾大停电等均造成严重的经济损失或者引发社会混乱。上述大停电事故中有的由单一电网元件故障开始,在运行方式不合理、继电保护不正确动作等原因综合作用下,引发连锁故障而扩大停电范围[3],有的则由持续时间长、作用范围广的自然灾害直接引发[4-5]。电网连锁故障的演化机理和大范围自然灾害的致灾过程均已有较多的研究。但是电网停电事故规律尤其是自然灾害引发电网停电事故的规律研究相对较少。迫切需要开展自然灾害引发电网停电事故规律的研究,以期减小大停电事故发生的风险,为避免和减少电网停电事故损失提供理论依据。
电力系统是一个典型的复杂系统。国内外学者基于复杂性科学对电网故障特性开展了一系列研究。国外学者基于比例赋权方差(SWV)、Hurst指数计算等方法,以负荷损失量[6-9]、受影响用户数[8-10]、停电时间[11]以及线路停运数量[11-12]等为衡量停电规模的指标发现或验证了电网停电事故的长程相关性和幂律特性,表明电网停电事故满足自组织临界性(SOC)。文献[12]基于OPA模型得出“从长远来看,部分消除停电风险的措施可能会增大停电风险”的结论。文献[9]建立了隐藏故障直流模型,研究了美国电网的级联故障特性,验证了美国停电事件的“停电规模—频率”满足幂律分布,并提出了减小大停电风险的策略。在停电事件的时间间隔分布方面,文献[6,10]基于北美电力可靠性委员会(NERC)公布的1984—1999年427条停电事故数据,计算其Hurst指数为0.6左右,而1994—1997年Hurst指数为0.5,发现了停电事件时间间隔累积概率分布呈现指数分布,并由此得出停电事件之间的联系来自于电网故障的自组织临界特性,而不是来自于停电事件触发因素之间的关联。文献[13]分析了1984—1998年和1984—2002年停电事件的时间间隔,认为其分布不满足指数分布,而是呈现明显偏离指数分布的胖尾特征,并根据“SOC系统的动态特性在时间间隔方面必须呈现出指数分布特征”的结论,对计算电网大停电动态模型的SOC方法提出了质疑。文献[8]结合了NERC公布数据和政府停电事故报告得出的1984—2006年停电事故的时间间隔分布满足非齐次泊松过程,指出文献[13]发现的电网停电事故引发因素之间不随机的根源在于引入齐次泊松过程模型。
国内研究人员发现电网故障的“停电规模—频率”等参数之间满足幂律特性[14-19],证明了电网系统是一个自组织临界系统。文献[15]证明了美国电网大停电事故的“负荷损失—停电概率”具有幂律关系,探讨了大停电规模分布的分形、分维特征,并指出电网系统结构存在自相似性,认为大停电规模具有可预测性。文献[16]基于复杂网络理论分析的中国大区电网具有小世界网络特性和无标度特性。文献[17]基于协同原理提出了电力系统大停电预测模型。文献[19]对配电网的停电事故进行了研究,表明了配电网故障在时间尺度上具有长程相关性,得出配电网故障具有自组织临界性特征的结论。文献[19]采用重标极差(R/S)分析方法和SWV的Hurst指数分析方法,揭示了广东电网停电事故的时间间隔具有长程正相关性和自相似性的特点。
输电线路是电网的重要组成部分。由于输电线路架设在野外,运行环境复杂多变,易受雷电[20]、山火[21]、冰灾[3]等灾害性天气影响而发生故障,输电线路故障是触发电网停电事故的主要因素[22]。根据美国颁布的白皮书中的数据显示,美国87%的电网大停电事故由气象灾害引发[23],中国气象灾害引发的输电线路故障占比也达到60.8%[24],2013年湖南电网220 kV及以上电压等级输电线路山火跳闸占总跳闸次数的36%。因此,研究各气象灾害对输电线路故障规律的影响尤为重要。
基于以上研究现状和结论,本文拟解决以下问题。
1)山火作为典型的复杂系统[25-26],其呈现自组织临界性,那么山火对输电线路形成的威胁是否具有幂律特性。
2)美国电网较大规模停电事件,对较大规模停电事件(以下简称停电事件)的定义为:事件失控导致电网丢失300 MW及以上的负荷时间持续达15 min;在紧急状态下甩负荷超过100 MW;超过5×104人次的用户中断供电超过1 h以上。序列的时间间隔满足指数分布,即认为电网停电的触发原因相互独立、随机,但未包含小规模输电线路跳闸故障,输电线路故障的时间间隔呈现的规律需要研究。
3)在山火的时间间隔满足幂律分布条件下[27],其引发的输电线路故障时间间隔是否遵循现有研究结论呈现指数分布,触发输电线路故障的同类事件之间是否随机、独立,各因素触发输电线路故障规律的差异性需要研究。
本文定义输电线路山火告警风险为输电线路走廊附近1 km以内且与输电线路之间无隔离带的山火。以湖南电网2005—2013年输电线路山火告警风险和故障数据为基础,首先分析了输电线路山火告警风险的“日告警数—频率”、输电线路故障的“时间间隔—频率”的累积分布函数(CCDF),然后基于Fano因子(Fano factor,FF)和Allan因子(Allan factor,AF)分析了输电线路故障时间序列的自相似性,探讨了输电线路山火告警风险和不同触发原因输电线路故障的“时间间隔—频率”分布特征,并解释了分布特征形成的物理机制。
1 数据来源与分析方法
本文山火数据来自输电线路山火广域监测预警系统,剔除掉工业火点、城市火点后,包括了中国范围内从2004—2013年3 653 d的全部565 685条山火信息。通过地理信息系统挑选出湖南省范围内山火33 514条,结合资产(设备)运维精益化管理系统(PMS2.0),所有220 kV及以上电压等级输电线路的投运时间和输电线路山火监测预警的时间,获得湖南电网输电线路山火告警风险1 934个。本文的输电线路故障数据以湖南电网为样本,收集2005—2013年发生的969条次220 kV及以上电压等级输电线路的故障。
由任意随机点过程得到1个不连续的时间点过程序列一般有2种方法:①区间计数值序列;②事件时间间隔序列。本文在分析输电线路山火告警风险时间分布规律时,采用区间计数序列,即将输电线路山火告警风险数据按时间顺序排列构成序列x(t),以时间长度τ将序列x(t)分割成m个不重叠的区间序列集合{Nk(τ)},Nk(τ)为以时间长度τ等间距划分的第k个窗口内输电线路山火告警风险次数。附录A图A1中输电线路山火告警风险区间计数值序列取时间长度τ为24 h。
在分析输电线路故障时间分布特征时,采用事件时间间隔序列方法,将输电线路故障按照发生时间顺序排列,两个连续故障之间的时间间隔定义为:
Δti=ti+1-ti
(1)
式中:ti为第i次事件发生时刻。
2 输电线路山火告警风险时间分布规律
2.1 输电线路山火风险季节周期性分布
本文以湖南省输电线路山火告警风险为例,作出2004—2013年输电线路山火告警风险的时间序列见附录A图A1。湖南电网输电线路山火告警风险具有明显的季节周期性,大部分输电线路山火告警风险发生在每年的1至4月,其主要原因如下。
1) 春节、清明祭祖和春耕烧荒导致潜在火源增多,例如在2012年4月3日湖南省共发生山火1 304处,形成输电线路山火告警风险184个,是统计的10 a中告警风险最多的一天。
2)受冬季冰灾的影响,植被易发生枯死和折损而含水量低,易燃等级高。
3)冬末初春为干旱时节,温度上升,日照时间变长,风大且风向多变,山火易发生和蔓延。
从附录A图A1可以看出,湖南省遭受2008年的严重冰灾后,其后3至4年内火点数目明显增多。一个重要的原因是大量的、远超平常的可燃物折损。2008年南方冰灾导致19个省的1.98×1011m2森林损毁,约占全国森林面积的13%,覆冰严重区域50%以上的树木因冰灾而折损、断裂,产生大量的易燃物[28]。
2.2 输电线路山火告警风险
对于复杂系统,假如其分布数据的“规模—概率”满足如下公式:
P(X>x)~x-a
(2)
式中:x为事件的规模;P(·)为所有事件X中规模大于规模为x的事件的概率,则说明该复杂系统数据的分布具有幂律特性;~表示正比于。
对幂律分布累积概率函数取对数。即
ln(P(X>x))=lnc-alnx
(3)
式中:a和c为常数。
根据式(3),以输电线路山火日告警风险数累积函数的对数为纵坐标,以输电线路山火日告警风险数的对数为横坐标,即将累积日告警风险数概率分布绘制在双对数坐标下。由于lnc和a为常数,具有幂律分布的概率分布曲线应呈直线,其在纵轴上的截距为lnc,斜率的绝对值为幂指数a。绘制湖南电网输电线路山火告警风险概率统计如图1、附录A图A2、图A3所示,计算得到不同时间段的幂指数如附录A表A1所示。
从图1、附录A图A2、图A3和附录A表A1可以看出,湖南电网输电线路山火告警风险分布的数据与拟合曲线的相关系数均在0.95左右,表明其具有明显的幂律特性,意味着可能在大多数日期内不会有或者有较少的输电线路山火告警风险。但是一旦发生山火告警风险,则可能密集爆发,说明输电线路山火告警风险存在丛集性。
在自然界的幂律分布中,幂指数表征的是事件发生不均匀分布的程度,幂指数越小则事件越集中于少数时段[29]。附录A表A1中2008—2012年时段的输电线路山火风险分布幂指数比2004—2007年时段的幂指数明显要小,说明特大冰灾后的4 a内,不仅输电线路山火告警风险数量远大于普通冬季,其山火发生的密集程度也有所增加。而2013年的幂指数大小则恢复到冰灾前幂指数大小,说明该次大型冰灾对输电线路山火分布的影响年限大约为4 a左右。
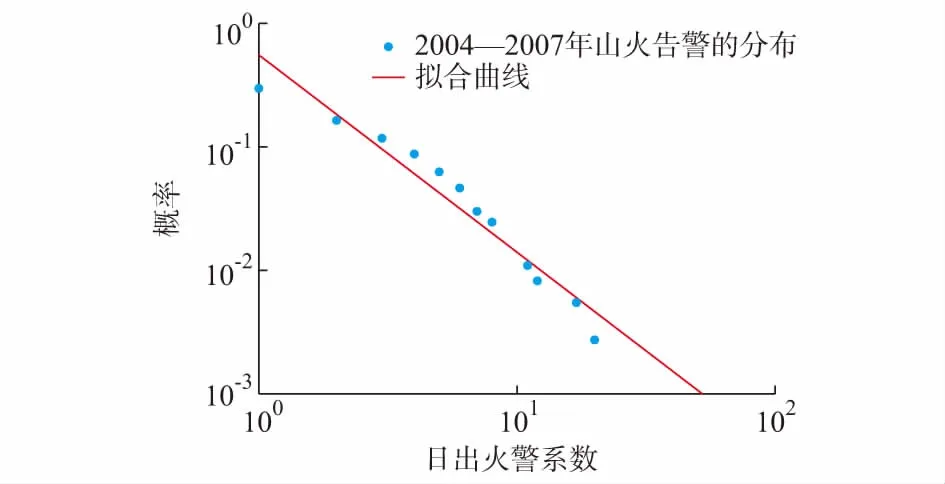
图1 2004—2007年输电线路山火告警幂律分布Fig.1 Power-law distribution of wildfire warning for transmission lines from 2004 to 2007
3 输电线路故障时间分布规律
3.1 输电线路故障时间间隔幂律分析
根据现有研究可知,电网停电事件触发原因的发生为泊松过程[11],停电事件之间的时间间隔为指数分布[7,8-10,13]。文献[6]则通过计算电网停电事故的Hurst指数约为0.5,得出“电网停电事件之间的触发原因之间相互独立、没有关联”的结论。
本文根据式(1)计算湖南电网输电线路故障的事件间隔直方图(interevent interval histogram,IIH),见附录B图B1,图中横坐标以2005年1月1日为时间起始点的输电线路故障时间(单位为min)。鉴于收集的数据时间跨度比较长、故障数据量比较多,故采用分段显示的方法,以每2 a为一个分段,共5个连续子图,图中每条垂直竖线代表一次输电线路故障。从附录B图B1中可知,湖南电网输电线路故障的时间间隔是非均匀的,有时密集发生,有时隔较长时间才发生,表明输电线路故障的发生具有较为明显的聚集现象。但通过IIH无法获得输电线路故障的发生是否随机,无法揭示这些时间差之间所包含的信息。
本文假设输电线路故障时间序列也为泊松分布,因此,输电线路故障将以时间间隔均值为λ的泊松过程随机发生。其概率分布函数f(x)可定义为:
f(x)=λe-λx
(4)
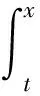
(5)
则输电线路故障时间间隔的累积分布函数(CCDF)为:
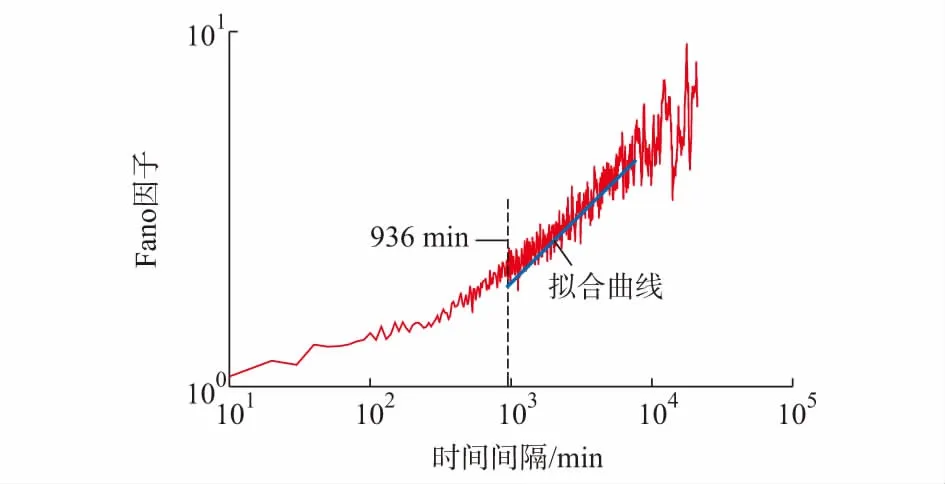
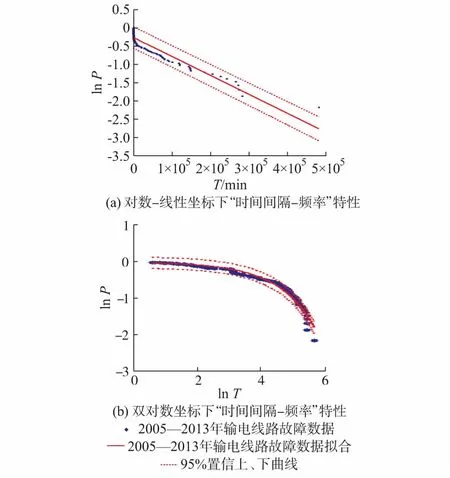
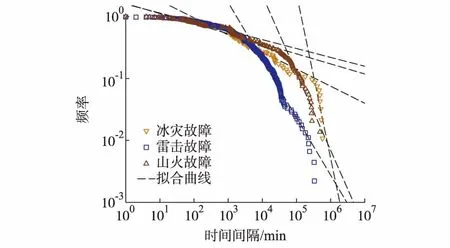
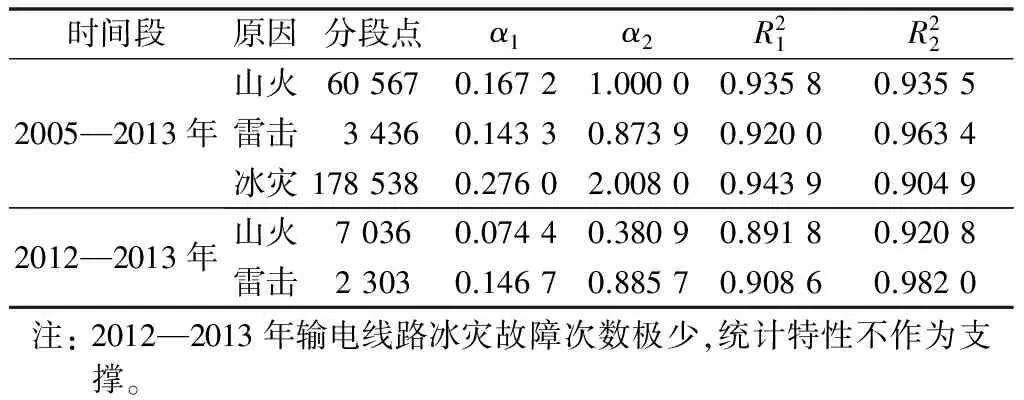
P(x)=P(X≥x)=1-P(X 1-F(x)~e-λx (6) 对式(3)两边同时取对数得: lnP(x)~-λx (7) 2005—2013年和2012—2013年输电线路故障“时间间隔—频率”结果在双对数坐标和对数—线性坐标上作图,如图2和附录B图B2所示。图2(a)中,双对数坐标“频率—时间间隔”呈现非线性关系,说明其不满足幂律分布关系,而在对数—线性坐标图2(b)中,lnP-lnT之间具有较好的线性关系。 图2 2005—2013年输电线路故障“时间间隔—频率”特性的CCDFFig.2 CCDF of transmission line faults for time interval-frequency from 2005 to 2013 这表明,输电线路故障时间序列的“频率—时间间隔”不具有幂律分布,而是随时间间隔增大呈现指数衰减,并且具有较好的鲁棒性。 通过3.1节的分析可知,计及所有触发原因的输电线路故障,“时间间隔—频率”未呈现出幂律分布,说明输电线路故障的时间序列未体现出分形特征。为了进一步地分析附录B图B1中的聚集现象,本节利用FF和AF研究2012—2013年湖南电网输电线路故障时间点过程序列,以判断输电线路故障时间点过程是否存在自相似的特征。 FF被定义为在时间标度为τ时的事件次数的方差与事件次数的平均值[30]。FF的表达式为: (8) 式中:avg(·)为求平均值函数;将时间标度τ以5 min为步长从5 min增加到整个时间跨度的十分之一,可以得到FF(τ)与τ的关系。 如果输电线路故障点过程呈现出自相似特征,则FF(τ)与τ满足幂律分布。类似地,可以采用AF识别分形指数在0~3之间的时间序列是否相似[31],AF的计算表达式为: (9) 图3给出了湖南电网输电线路故障时间序列的FF曲线。从图中可以看出在936 min以后,FF曲线呈幂律分布。τ=936 min被称为自相似开始时间,标志着标度行为的下界[32]。随着时间标度的增加,FF曲线呈现出明显的线性趋势,表明输电线路故障时间序列具有自相似特征。当936 min <τ< 8 900 min时,FF曲线的标度指数αF=0.460 3±0.014 0。在曲线早期的100 min以前,FF曲线呈现平坦的趋势,表明在较小的时间尺度上,输电线路故障序列呈现出类似泊松序列的行为,输电线路故障发生时间上不存在相关性。在100~936 min之间被认为是时间序列时间标度行为发生转变的阶段,序列从泊松行为向自相似特征转化。 图3 输电线路故障时间序列Fano因子Fig.3 Fano factor of time sequence of transmission line fault 由此可以看出,在输电线路故障的发生时间存在两个尺度上的动力学行为。一个是时间间隔小于τt的过程,对应于外部环境中输电线路故障触发因素的持续时间。例如一次山火高发期或者持续冻雨过程的持续时间。另一个是时间间隔长度大于τt的过程,对应于外部环境中输电线路故障触发因素的重现期。 附录B图B3给出了湖南电网输电线路故障时间序列的AF的结果。当2 260 min<τ<8 940 min时,输电线路故障的标度指数αA=0.591 7±0.029 2,拟合直线的相关系数R2为0.68,本文认为输电线路故障时间序列仍具有一定的自相似性。 如图3、附录B图B3所示,2个特征时间尺度范围之间存在着2个明显的交叉点,分别为τ1≈936 min,τ2≈6 980 min,τ1′≈2 260 min,τ2′ ≈8 200 min。FF和AF在交叉点两侧明显具有不同的特征,这种不同源于交叉点两侧的时间尺度范围具有不同的时间动力过程,区域1和区域2之间交叉点τ1为自相似起始时间尺度,表示外部环境中输电线路故障触发因素的持续时间内输电线路故障的丛集性,而τ2则可解释为外部环境中输电线路故障触发因素的重现期,表示不同触发故障因素之间的丛集性。 对于分形的随机点过程,其“频率—时间间隔”应满足幂律分布。由以上分析可知,输电线路故障的时间分布不是分形点过程。但利用统计变量FF和AF则发现其满足自相似性。因此,输电线路故障的时间序列是具有自相似性的非分形的“分型率”随机点过程[32]。 通过计算输电线路时间间隔的累积概率分布来分析山火、雷击、冰灾等原因触发的输电线路故障的规律,如图4、附录B图B4至图B6所示。 图4 2005—2013年输电线路山火故障的CCDFFig.4 CCDF of for transmission lines faults caused by wildfire from 2005 to 2013 输电线路山火、雷击和冰灾故障的“时间间隔—频率”在双对数曲线(图4(b))上,呈现出有限尺度幂律特性,并在不同时间尺度位置有明显的转折点,如图5和附录B图B7所示,分别对两段幂律曲线进行直线拟合,其中雷击、火山、冰灾这3类故障所占比例分别为46.12%,14.89%,9.89%,获得其幂律特性见表1。2005—2013年和2012—2013年的输电线路故障时间间隔均呈现分段幂律特性,具有时间鲁棒性。 图5 2005年—2013年各类故障“时间间隔-频率”特性的CCDFFig.5 CCDF of different transmission line faults for time interval-frequency from 2005 to 2013 时间段原因分段点α1α2R21R22山火605670.16721.00000.93580.93552005—2013年雷击34360.14330.87390.92000.9634冰灾1785380.27602.00800.94390.90492012—2013年山火70360.07440.38090.89180.9208雷击23030.14670.88570.90860.9820注:2012—2013年输电线路冰灾故障次数极少,统计特性不作为支撑。 输电线路山火故障主要发生在春节、春耕、清明等山火高发期,时间间隔分段点取值较大。2005—2013年全省输电线路山火故障“时间间隔—频率”幂律曲线的分段点τf1位置大约为60 567 min,最大的故障时间间隔为482 450 min,对应为335 a,2012—2013年幂律曲线的分段点τf1′ 位置大约为7 036 min,最大的故障时间间隔为482 450 min,对应为335 a。 附录B图B4为湖南电网输电线路雷击故障的“时间间隔—频率”在双对数坐标上的数据,由于湖南电网雷击故障极为频繁[33],因此输电线路雷击故障的时间间隔相对较小,长时间间隔的故障频率较低。如2005—2013年全省输电线路雷击故障“时间间隔—频率”幂律曲线的分段点τl1位置大约3 436 min,其故障最大时间间隔为334 839 min,对应为232.5 a。2012—2013年幂律曲线的分段点τl1′位置大约为2 303 min,最大的故障时间间隔为334 839 min,对应为126.8 a。 冰灾引发输电线路故障只发生在冬、春的覆冰期,其时间间隔取值在上述三种自然灾害触发因素中最大,2005—2013年全省输电线路冰灾故障“时间间隔—频率”幂律曲线的分段点τi1位置大约为178 538 min,最大的故障时间间隔为577 405 min,对应约为401 a。 在自然界中其他复杂系统的“事件规模—频率”也出现这种幂律曲线分段的现象[34-37]。如森林火灾幂律曲线的转折点国内外研究较多,文献[36-37]认为小面积火灾和大面积火灾累积概率分布与幂律分布理论曲线存在差异的主要原因是统计数据的缺失和人为防火措施、地形、风速等外部环境因素的作用。输电线路故障“时间间隔—频率”呈现分段现象的主要原因为:①受数据的限制,湖南电网110 kV及以下电压等级的输电线路故障未在统计和分析的范围内;②极端自然灾害的发生概率增加,且各类灾害的高发期变长、强度增大,如极端干旱、特大冰灾,导致输电线路发生故障的可能性增加,输电线路故障出现长时间间隔的概率变小。 尽管电网灾害防治技术的提升与应用,但受地域广袤、灾害影响范围大、治理装备难以全覆盖等原因,往往其作用在于针对某一个具体的灾害过程有准备地防治以减少输电线路故障,非完全杜绝电网灾害故障的发生。因此,综合两因素的作用,输电线路故障时间间隔偏离单一幂律曲线,呈现“L形”分段的幂律关系。 上述研究结论与本文第3节的FF和AF计算结果一致,区分了各触发输电线路故障因素的持续时间和外部环境中输电线路故障触发因素重现期的丛集性。 基于上述分析可知,湖南电网各单一因素触发的输电线路故障时间间隔并不满足指数分布,意味着各输电线路故障因素和触发因素之间并不独立。这与文献[6,10]中阐述的较大规模停电事件之间触发因素相互独立的结论并不完全一致。正是这样的关联关系使得单因素触发的输电线路故障时间间隔呈现分段幂律曲线的特征。通过揭示输电线路故障时间间隔序列具有良好的统计自相似性,说明可以根据历史数据对电网故障进行较好地预测[16,22]。同时证明了文献[13]中关于“SOC系统的事件时间间隔必须呈现指数分布”的结论是错误的。电网停电事故复杂系统的自组织临界特征与时间间隔分布相互独立。复杂系统呈现的特性与复杂系统输入参数的特征并不相同。这与文献[8]的结论一致。 随着湖南电网系列防山火措施的应用,2012—2013年山火故障仅占湖南电网比例的14.28%。附录B图B8为2012—2013年湖南电网剔除山火故障前后输电线路故障“时间间隔—频率”特性。从附录B图B5可以发现,山火故障使湖南电网输电线路故障时间分段幂律曲线的转折点变小,但并不明显,其区别主要体现在最大时间间隔由69 977 min减小至46 908 min,可见山火故障对输电线路故障的时间间隔分布规律没有本质性的影响。 本文将输电线路山火和输电线路故障数据视作时间点过程序列,基于常用的点过程序列分析方法,对湖南省2005—2013年输电线路山火和输电线路故障时间点序列进行了深入分析,得到如下结论。 1)通过计算输电线路山火风险告警的累积分布函数,发现了输电线路山火风险告警的“日山火告警风险数—频率”满足幂律特性,说明其时间点过程与山火时间分布一样具有时间从集性。 2)通过分析2008年特大冰灾前后的输电线路山火告警幂律分布特征,验证了大型冰灾加大了植被的折损量,为山火提供更多的可燃、易燃物而增加了输电线路山火告警风险的集中程度。 3)发现输电线路故障的“时间间隔—频率”满足指数分布,进一步计算FF和AF发现输电线路故障时间序列具有自相似性和输电线路故障具有2个时间尺度上的动力学过程。 4)分析了湖南电网冰灾、雷击、山火等主要输电线路故障因素的“时间间隔—频率”不满足指数分布而呈现分段幂律特征,发现各因素导致的输电线路故障幂律曲线转折点对应时间尺度从大到小分别为冰灾、山火和雷击。并分析了导致该结果的原因是外部环境的丛集性特征。 5)输电线路故障发生时间之间存在关联,那么输电线路故障的规模和时间间隔之间的关系将是下一步研究的重点,为减少大面积停电风险提供依据。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 参 考 文 献 [1] 甘德强,胡江溢,韩祯祥.2003年国际若干停电事故思考[J].电力系统自动化,2004,28(3):1-4. GAN Deqiang, HU Jiangyi, HAN Zhenxiang. Thinking over several blackouts in 2003[J]. Automation of Electric Power Systems, 2004, 28(3): 1-4. [2] 邵瑶,汤勇,易俊,等.土耳其“3·31”大停电事故分析及启示[J].电力系统自动化,2016,40(23):9-14.DOI:10.7500/AEPS20160412004. SHAO Yao, TANG Yong, YI Jun, et al. Analysis and lessons of blackout in turkey power grid on March 31, 2015[J]. Automation of Electric Power Systems, 2016, 40(23): 9-14. DOI: 10.7500/AEPS20160412004. [3] 薛禹胜,吴勇军,谢云云,等.停电防御框架向自然灾害预警的拓展[J].电力系统自动化,2013,37(16):18-26. XUE Yusheng, WU Yongjun, XIE Yunyun, et al. Extension of blackout defense scheme to natural disasters early-warning[J]. Automation of Electric Power Systems, 2013, 37(16): 18-26. [4] 薛禹胜,费圣英,卜凡强.极端外部灾害中的停电防御系统构思(一)新的挑战与反思[J].电力系统自动化,2008,32(9):1-6. XUE Yusheng, FEI Shengying, BU Fanqiang. Upgrading the blackout defense scheme against extreme disasters: Part Ⅰ new challenges and reflection[J]. Automation of Electric Power Systems, 2008, 32(9): 1-6. [5] 薛禹胜,费圣英,卜凡强.极端外部灾害中的停电防御系统构思(二)任务与展望[J].电力系统自动化,2008,32(10):1-5. XUE Yusheng, FEI Shengying, BU Fanqiang. Upgrading the blackout defense scheme against extreme disasters: Part Ⅱtasks and prospects[J]. Automation of Electric Power Systems, 2008, 32(10): 1-5. [6] CARRERAS B A, NEWMAN D E, DOBSON I, et al. Initial evidence for self-organized criticality in electric power system blackouts[C]// Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, January 7, Maui, USA, 2000: 6p. [7] CARRERAS B A, NEWMAN D E, DOBSON I, et al. Evidence for self-organized criticality in electric power system blackouts[C]// Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, January 6, Maui, USA, 2001: 6p. [8] CARRERAS B A, NEWMAN D E, DOBSON I. North American blackout time series statistics and implications for blackout risk[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4406-4414. [9] CHEN J, THORP J S, DOBSON I. Cascading dynamics and mitigation assessment in power system disturbances via a hidden failure model[J]. Electrical Power and Energy Systems, 2005, 27: 318-326. [10] CARRERASB A, NEWMAN D E, DOBSON I, et al. Evidence for self-organized criticality in a time series of electric power system blackouts[J]. IEEE Transactions on Circuits and Systems, 2004, 51(9): 1733-1740. [11] CHEN J, THORP J, PARASHAR M. Analysis of electric power system disturbance data[C]// Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, January 6, Maui, USA, 2001: 6p. [12] NEWMAN D E, CARRERAS B A, LYNCH V E, et al. Exploring complex systems aspects of blackout risk and mitigation[J]. IEEE Transactions on Reliability, 2011, 60(1): 134-143. [13] WERON R, SIMONSEN I. Blackouts, risk, and fat-tailed distributions[J/OL]. Practical Fruits of Econophysics, 2006. https://link.springer.com/chapter/10.1007414-431-28915-1_39. [14] 于群,郭剑波.电网停电事故的自组织临界性及其极值分析[J].电力系统自动化,2007,31(3):1-3. YU Qun, GUO Jianbo. Self-organized criticality and extreme statistics analysis of electric power system blackouts[J]. Automation of Electric Power Systems, 2007, 31(3): 1-3. [15] 曹一家,江全元,丁理杰.电力系统大停电的自组织临界现象[J].电网技术,2005,29(15):1-5. CAO Yijia, JIANG Quanyuan, DING Lijie. Self-organized criticality phenomenon for power system blackouts[J]. Power System Technology, 2005, 29(15): 1-5. [16] 郭剑波,于群,贺庆.电力系统复杂性理论初探[M].北京:科学出版社,2012:59-150. [17] 曹一家,丁理杰,江全元,等.基于协同学原理的电力系统大停电预测模型[J].中国电机工程学报,2005,25(18):13-19. CAO Yijia, DING Lijie, JIANG Quanyuan, et al. A predictive model of power system blackout based on synergetic theory[J]. Proceedings of the CSEE, 2005, 25(18): 13-19. [18] 晁岱峰,杨军选,苏盛,等.濮阳配电网故障的自组织临界性及其诱因[J].电网技术,2011,35(1):72-75. CHAO Daifeng, YANG Junxuan, SU Sheng, et al. Self-organized criticality and its cause of faults in Puyang distribution system[J]. Power System Technology, 2011, 35(1): 72-75. [19] 徐立新,杨建美,潮铸,等.电网故障时间间隔的统计分布及非线性特征分析[J].电网技术,2013,37(12):3482-3488. XU Lixin, YANG Jianmei, CHAO Zhu, et al. Statistical distribution and nonlinear characteristic analysis of fault time intervals in power grids[J]. Power System Technology, 2013, 37(12): 3482-3488. [20] 谢云云,薛禹胜,王昊昊,等.电网雷击故障概率的时空在线预警[J].电力系统自动化,2013,37(17):44-51. XIE Yunyun, XUE Yusheng, WANG Haohao, et al. Space-time early-warning of power grid fault probability by lightning[J]. Automation of Electric Power Systems, 2013, 37(17): 44-51. [21] 吴勇军,薛禹胜,陆佳政,等.山火灾害对电网故障率的时空影响[J].电力系统自动化,2016,40(3):14-20.DOI:10.7500/AEPS20151110015. WU Yongjun, XUE Yusheng, LU Jiazheng, et al. Space-time impact of forest fire on power grid fault probability[J]. Automation of Electric Power Systems, 2016, 40(3): 14-20. DOI: 10.7500/AEPS20151110015. [22] 王昊昊,罗建裕,徐泰山,等.中国电网自然灾害防御技术现状调查与分析[J].电力系统自动化,2010,34(23):5-10. WANG Haohao, LUO Jianyu, XU Taishan, et al. Questionnaire survey and analysis of natural disaster defense techniques of power grids in China[J]. Automation of Electric Power Systems, 2010, 34(23): 5-10. [23] Executive Office of the President. Economic benefits of increasing electric grid resilience to weather[R/OL]. USA, 2013. http://www.docin.com/p-991796325.html. [24] 薛禹胜,吴勇军,谢云云,等.复合自然灾害下的电力系统稳定性分析[J].电力系统自动化,2016,40(4):10-18.DOI:10.7500/AEPS20151110016. XUE Yusheng, WU Yongjun, XIE Yunyun, et al. Power system stability analysis for intercurrent natural disasters[J]. Automation of Electric Power Systems, 2016, 40(4): 10-18. DOI: 10.7500/AEPS20151110016. [25] SONG W, FAN W, WANG B, et al. Self-organized criticality of forest fire in China[J]. Ecological Modelling, 2001, 145(1): 61-68. [26] SONG W, FAN W, WANG B. Influences of finite-size effects on the self-organized criticality of forest-fire model[J]. Chinese Science Bulletin, 2002, 47(3): 177-180. [27] SONG Weiguo, WANG Jian, SATOH Kohyu, et al. Three types of power-law distribution of forest fire in Japan[J]. Ecological Modelling, 2006, 196(3):527-532. [28] XIAO Y. Effects of litter caused by ice storm input on soil carbon, nitrogen and greenhouse cases flux in subtropical forests of China[D/OL]. Beijing: Chinese Academy of Forestry, 2012. [29] LU Jiazheng, ZHOU Tejun, ZHANG Hongxian, et al. Self-organized criticality in wildfire time series from China[J]. Natural Hazards Review, 2017, 18(4): 14-17. [30] FANO U. Ionization yield of radiations Ⅱ, the fluctuations of the number of ions[J]. Physical Review, 2008, 72(1): 26-29. [31] ALLAN D W. Statistics of atomic frequency standards[J]. Proceedings of the IEEE, 1966, 54(2): 221-230. [32] THURNER S, LOWEN S, FEURSTEIN M, et al. Analysis, synthesis, and estimation of fractal-rate stochastic point processes[J]. Fractals, 1997, 5(4): 565-595. [33] 蒋正龙,陆佳政,何俊佳,等.湖南省雷电活动及其规律的分析[J].高电压技术,2011,37(10):2431-2436. JIANG Zhenglong, LU Jiazheng, HE Junjia, et al. Analyses of lightning activity and its law in Hunan province[J]. High Voltage Engineering, 2011, 37(10): 2431-2436. [34] WILSON A. Landscape genetics of highly disturbed arable systems: insights gained from investigating a small mammal species[D/OL]. St Andrews: University of St Andrews, 2014. [35] MELTZER M I, HASTINGS H M. The use of fractals to assess the ecological impact of increased cattle population: case study from the Runde Communal Land, Zimbabwe[J]. Journal of Applied Ecology, 1992, 29(3): 635-646. [36] RICOTTA C, ARIANOUTSOU M, DIAZ R. et al. Self-organized criticality of wildfires ecologically revisited[J]. Ecological Modelling, 2001, 141(1): 307-311. [37] HASTINGS H M, SUGIHARA G. Fractals: a user’s guide for the natural sciences[M/OL]. Oxford: Oxford University Press, 1994.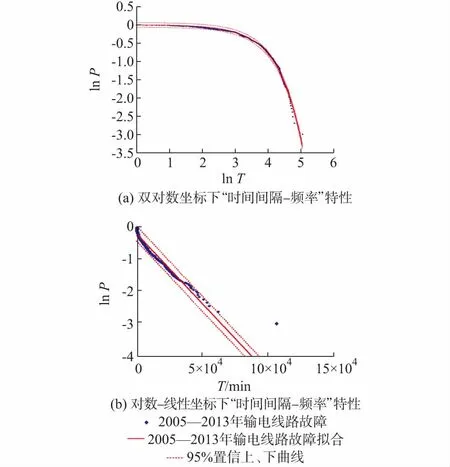
3.2 FF因子和AF因子分析
4 自然灾害对输电线路故障时间间隔分布特性影响及对比
5 结论
