考虑充放电能量不均衡的双电池系统状态评估与控制策略

林 莉, 金 鑫, 朱丽云, 张向伍, 赵晓焱, 杨仕燕

(1. 输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044; 2. 国网南阳供电公司, 河南省南阳市 473000)

0 引言

近年来,风电以其无污染、能源可持续、技术成熟等优点作为绿色友好型能源已经得到广泛应用。但因风能具有较强的随机性、间歇性以及不可准确预测性,风电输出功率呈现明显的波动特征,直接并网将给电力系统安全稳定运行带来巨大的挑战。而储能凭借其可充可放的运行特性,可灵活、快速地调节系统电能平衡以平滑风电输出波动功率,减少风电并网对系统的影响。

现阶段储能技术尚不成熟,设备成本相对较高,极大地影响了风储联合系统的经济性[1]。对于电池储能系统,运行过程影响其经济性的重要因素是使用寿命。其中,放电深度、充放电转换次数等可认为是影响其使用寿命的主要原因[2]。文献[3]从循环次数角度建立电池储能系统寿命评估模型,在控制过程中通过优化控制参数延长电池使用寿命;文献[4-5]考虑电池的荷电状态(SOC)实时优化,通过优化放电深度,避免过充过放以延长储能寿命。文献[6]考虑电池充放电的不规则性,通过合理选择混合储能系统协调控制参数,延长锂电池使用寿命。文献[7]建立了多因素聚合寿命模型,通过模糊策略优化控制步长,从而延长了电池使用年限。文献[8]基于放电深度和循环次数对电池的影响,建立了微网应用中的电池模型。为了减少电池充放电次数改变对电池寿命损耗的影响,文献[9]分析了放电深度与电池寿命的关系,并提出了双锂电池—超级电容的混合储能的工作模式,将锂电池分为两个单元分别独立执行充电、放电任务,控制电池每循环周期内运行在最佳放电深度状态,以此提高电池的使用寿命。但实际工作中,超级电容已将频繁变化的高频波动分量平抑,锂电池用于平抑变化缓慢的低频波动分量,未能充分发挥双电池系统的效果。文献[10]在PSCAD/EMTDC平台上搭建了接入风电场的双电池储能系统(DBESS)模型,提出了在给定放电深度下的DBESS协调运行控制策略。文献[11]根据实测数据,搭建了充放电任务独立执行的电池储能应用模型,从减少寿命损失的角度,分析了采用该运行模式的经济性。然而,双电池组协调运行模式虽能在一定程度上延长电池使用寿命,但上述文献均未考虑储能系统长期运行的稳定性。

本文在已有研究的基础上,讨论了DBESS长期运行过程中因充放电能量不均衡,可能出现的充/放电能力不足的极端运行情况,根据电池运行的实时状况和功率波动特性,提出了能够表征DBESS运行工况的充放电饱和能力指标和充放电运行平稳度指标,并设计了模糊控制策略以自适应调节低通滤波器的时间常数,从而实时优化控制双电池组的SOC,保证DBESS长期稳定运行的可行性。

1 考虑使用寿命的DBESS运行模式及其数学模型

为了延长电池的使用寿命,本文将风电场中的电池储能系统分为A和B两组,采用充放电任务分开独立执行的运行策略,使得电池单元能够运行在最佳放电深度下,从而有效减少频繁充放电对电池的损害。附录A图A1给出了含DBESS的风电场结构图,其中,Pw为风电场输出的实际功率,Pb为电池的充放电功率,Pg为并网风电功率。能量管理系统根据风电场输出的风电功率以及电池组的运行状况确定电池组A和电池组B的充放电任务。当变流器AC-DC工作在整流状态时,储能系统将风电场剩余的能量储存;当变流器AC-DC工作在逆变状态时,储能系统则释放能量以补偿风电缺额功率。

1.1 基于充/放电任务独立的DBESS运行原理

本文针对电池充放电状态频繁切换造成使用寿命降低的问题,将电池分为A和B两组,采用充、放电任务分开执行的运行模式[9,12-13],使电池组工作在给定的最佳放电深度,以延长电池的实际使用寿命,并根据两组电池的SOC判断两组电池是否发生充放电状态转换。假定初始运行时,充电电池组A(B)的SOC值为(1-Dref)/2,只执行充电任务,放电电池组B(A)的SOC值为(1+Dref)/2,只执行放电任务,确保同一时刻A和B两组电池组不同时工作。其中,Dref为最佳运行时的放电深度,其值可根据电池厂家提供的生产数据,结合文献[9]所提电池寿命衰减评价方法计算获得。在最佳放电深度运行模式下,当充电电池组A(B)运行至SOC值为(1+Dref)/2、放电电池组B(A)运行至SOC为(1-Dref)/2时,切换两组电池的充放电运行模式。此时,电池组A(B)作为放电电池组,只释放能量以补偿风电波动缺额功率,电池组B(A)作为充电电池组,只吸收风电剩余能量。

然而,由于运行过程中风电波动的不确定性,两组电池的充放电过程不一致,充放电总能量不均衡,因此多数情况下难以实现两组电池同时达到运行模式切换的临界状态。为了避免电池发生过充过放现象,当其中一组电池SOC值到达临界状态转换值时,储能系统即可进行充放电运行模式切换,如附录A图A2所示。

1.2 DBESS充放电运行数学模型

由于在风电波动功率平抑过程中,电池分为A和B两组,将充、放电任务分开单独执行:当一组电池工作,则另一组电池处于待机状态。因此,每组电池的额定充放电能力为整个储能系统的1/2,即

(1)

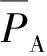
根据DBESS的运行原理,电池组A和B的SOC递推模型如式(2)所示。

(2)

式中:CSOCA(t)和CSOCB(t)分别为t时刻电池组A和电池组B的SOC;ηc和ηd分别为电池的充电效率和放电效率;ηinv为变流器的转换效率;Pb(t)为t时刻电池的实际充放电功率；SAc,SAd,SBc,SBd分别为电池组A和电池组B的充、放电运行状态标志位,为1表示是,为0表示非;wc和wd分别为t时刻储能系统是否执行充电和放电任务,为1表示是,为0表示非。电池组A和B的充放电状态与其充放电标志位关系见附录A表A1。

为了防止电池过充过放,应对每组电池的平抑功率进行限幅,即t时刻系统所能平抑的波动功率Pb(t)应满足一定的约束条件,即

Pxu，max，ch(t)≤Pb(t)≤Pxu，max，dis(t)

(3)

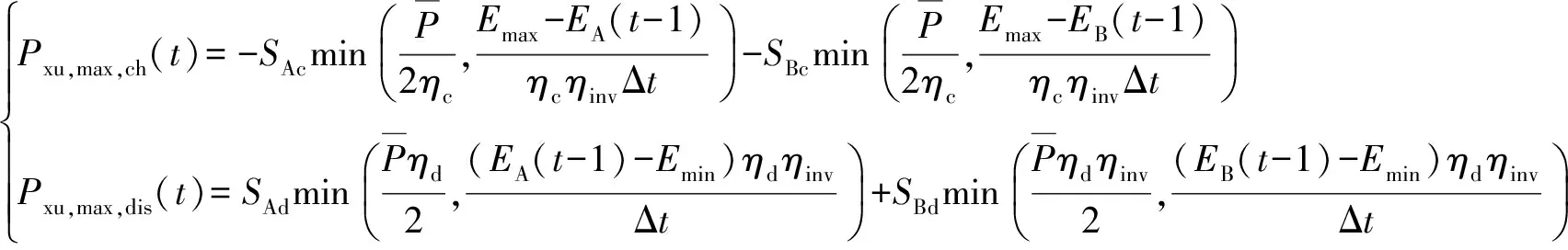
(4)

式中:Pxu,max,ch(t)为t时刻受DBESS功率和剩余容量限制得到的最大可充电功率,其值为负;Pxu,max,dis(t)为t时刻DBESS由额定功率和剩余容量限制得到的最大可放电功率,其值为正;Emax为运行过程中电池组最大允许剩余能量值;Emin为最小允许剩余能量值;EA(t-1)和EB(t-1)分别为t-1时刻电池组A和电池组B的剩余能量;Pxu,max,ch(t)和Pxu,max,dis(t)取值由DBESS的运行模式、电池组自身特性及剩余容量决定。

2 DBESS运行状态评估

为了避免电池发生过充过放现象,只要其中一组电池达到状态转换临界值,即进行充放电状态转换。但长期如此运行,可能致使储能系统进入因放电能力或充电能力不足的极端运行区间,见图1。

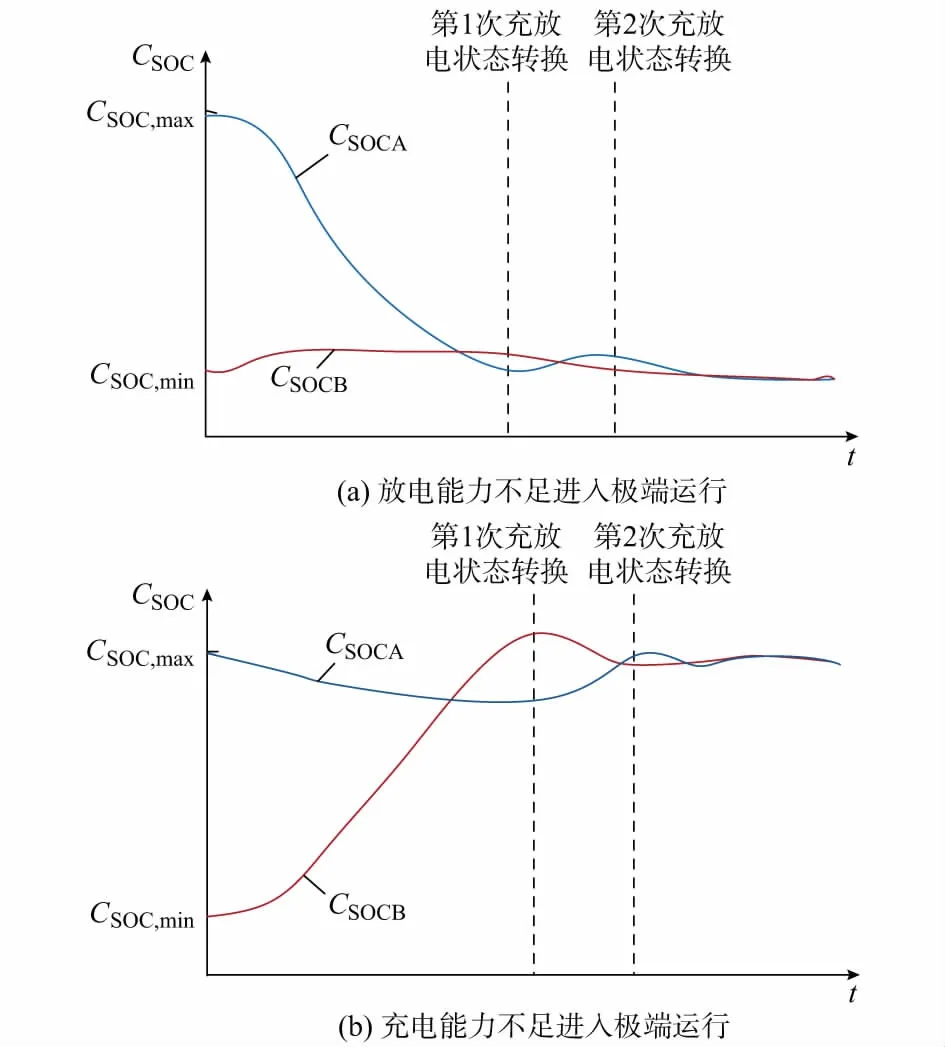
图1 DBESS不稳定运行情况Fig.1 Unstable operation of DBESS

以储能系统因放电能力不足进入极端运行区间为例进行分析。当放电电池组A到达最佳放电深度时,充电电池组B在该过程中充电总量较少,CSOCB可能在充电初始状态附近,若此时进行充放电状态转换,电池组B开始执行单独放电的工作任务,因上一运行阶段充电量较少,其可放电能量极少,两组电池将很快再次进行充放电状态转换,同时,执行放电任务的电池组A由于上一运行阶段充电量较少,CSOCA值较小,可放电能量极少。如此循环工作,当两电池组的SOC值同时到达最低限值时,DBESS的可放电能力极弱,将不能满足平抑波动功率对释放能量的需求,不仅极大地影响平抑效果,也难以维持电池组的长期稳定运行。因充电能力不足进入极端运行区间的情况与此类似,此处不再详述。

两组电池的SOC值是影响DBESS运行状态转换的关键参量,本节根据两电池组的实时运行情况,提出能够表征DBESS运行工况的充放电饱和能力指标和充放电运行平稳度指标。

1)充放电饱和能力指标:该指标用来衡量当DBESS以最佳放电深度运行时,t时刻DBESS平滑风电出力的能力。

(5)

(6)

式中:CSOC,max和CSOC,min分别为最佳运行模式下,电池组SOC可达到的最大值和最小值;εch(t-1)和εdis(t-1)分别为上一时刻后,充电电池组可吸收能量和可释放能量的能力;R(t)∈[-1,1],表示归一化后的t时刻工作电池组的平滑风电出力的能力。当R(t)>0时,表示此刻充电电池组工作,其值越接近1,则反映该电池组此前已释放越多能量,储能系统充电能力越强;当R(t)<0时,表示此刻放电电池组工作,其值越接近-1,则反映该电池组此前已吸收越多能量,储能系统放电能力越强。

2)充放电运行平稳度指标:该指标用来反映因运行过程中充放电能量不均衡,DBESS是否具有进入可充电或可放电能力不足的趋势。

ΔCAB(t-1)=εch(t-1)-εdis(t-1)

(7)

式中:ΔCAB(t-1)为上一时刻充放电结束后,受剩余容量限制,充电电池组的充电能力与放电电池组的放电能力之间的偏差。若给定最佳放电深度为0.8时,则ΔCAB(t-1)∈[—0.8,0.8]。

当ΔCAB(t-1)大于0时,表示相较于充电电池组吸收能量,放电电池组已放出较多的能量平滑风电波动功率,若不及时调整,放电电池组将较充电电池组先达到临界转换值,其数值越大,越不利于双电池系统的协调稳定运行;反之,当ΔCAB(t-1)小于0时,则表示相较于放电电池组释放能量,充电电池组已吸收较多的能量,若此时不调整,充电电池组将较放电电池组先达到临界转换值,其数值越大,越不利于DBESS的协调稳定运行。

3 SOC实时优化控制

为了确保DBESS长期稳定运行,应根据储能系统运行状况,实时调节两电池组的电量以维持良好的运行能力。

3.1 滤波时间常数及平抑效果评价指标

实际运行过程中,风电功率参考值Pgref通常可由风电输出功率Pw经过一阶低通滤波后得到:

(8)

式中:s为微分算子;T为滤波时间常数,其值大小会影响平滑效果;Pbref为DBESS所需平抑的波动功率量,若其值大于零,则储能系统释放能量以补偿功率缺额,反之,若风电功率剩余,DBESS吸收剩余能量。

由附录A图A3所示的Pbref传递函数波特图可知,当滤波时间常数为T1时,电池储能系统需要平抑Pw中频率大于截止频率ω1的波动分量。根据文献[14]对风电功率波动特性及其对电网的影响的分析,储能设备主要用于平抑频段为0.01～1 Hz的风电波动功率,由此可大致确定滤波器时间常数T的范围。

进一步地,为了评估DBESS对风电波动功率的平抑效果,本文提出某频段波动功率含量Rv指标,用于量化特定频率段波动分量相对于原始风电功率所有频段波动分量的大小,定义如下:

(9)

式中:F为波动频率段;PF(f)为在频段F内,频率等于f的波动功率分量。等式右边分子表示频段F内的波动分量绝对值总和,分母表示风电输出功率Pw所有频段波动分量绝对值总和。若Rv(F)的值越大,则该频段的波动分量越大。

3.2 模糊控制策略设计

为解决双电池系统可能因充放电能力不足进入极端运行区间的问题,本小节根据所提充放电饱和能力指标R(t)和充放电运行平稳度指标ΔCAB(t-1)确定合适的滤波时间常数修正系数λ(t),从而动态调整风电并网参考功率Pgref,改变电池组充放电任务,以实现DBESS长期稳定运行。所设计模糊控制器如图2所示。

附录A图A4给出了本文所设计模糊控制器的输入输出隶属函数。其中,输入R(t)和ΔCAB(t-1)均为连续域,对应的语言变量均采用{NB,NS,ZE1,ZE2,PS,PB},分别表示当前输入值为{负大,负小,负适中,正适中,正小,正大};输出λ(t)为离散域{-1.0,-0.6,-0.2,0,0.2,0.6,1.0},对应的语言变量为{NB,NM,NS,ZO,PS,PM,PB}。

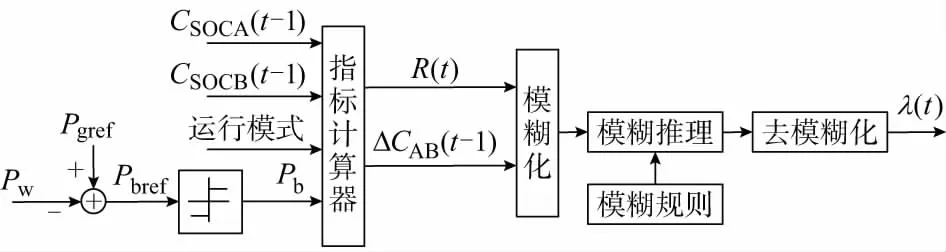
图2 模糊控制器设计Fig.2 Design of fuzzy controller

以t时刻储能系统充电,即R(t)为正为例,说明设计模糊控制策略的基本思想为:若ΔCAB(t-1)为负,且其值较大,则应降低滤波时间常数T,使Pgref对Pw的跟踪速度变快,从而相对减小储能系统的充电功率,以减缓充电电池组SOC的提升速度,防止充电电池组过早到达状态转换临界值;反之,若ΔCAB(t-1)为正,则应增大T以减缓Pgref对Pw的跟踪,从而相对增大DBESS的充电功率,有助于加快提升充电电池组SOC值,缩小与放电电池组的差距。所设计模糊控制与R(t)和ΔCAB(t-1)的正负符号和绝对值的大小相关,具体控制细则如附录A表A2所示。

采用重心法进行去模糊化,可得任意t时刻滤波时间常数修正系数:

(10)

式中：μ1i(R(t))和μ2i(ΔCAB(t-1))分别对应第i个输入量R(t)和第j个输入量ΔCAB(t-1)的隶属度值；λij为与之相对应的输出。

则当前时刻滤波时间常数为:

T=T0+λ(t)ΔT

(11)

式中:T0为初始时刻设置的滤波时间常数;ΔT为最大可调节滤波时间常数,其值与T0选取以及对波动功率平滑效果的要求有关。

4 仿真验证

为了验证上节所提模糊控制策略的有效性,在MATLAB/Simulink平台上进行仿真。风电输出功率取自某风电场实测数据,总装机容量为16 MW;储能系统由A和B两组电池构成,采用附录A式(A3)所示电池等效模型,额定容量为13 MW/15 MW·h,最佳放电深度给定为0.8,电池组A和B初始SOC值分别为0.1和0.9,分别作为充电电池组和放电电池组;电池充放电效率均为0.9,变流器转换效率为0.85。滤波时间常数初始值T0设定为120 s;时间常数调节基值ΔT设为20 s。

本次仿真主要以储能系统因放电能力不足进入极端运行情况为例,而系统因充电能力不足进入极端运行状况的分析与此类似,本文不进行详述。

1)SOC优化控制效果分析

图3所示为有无采用所提模糊控制策略,两电池组的SOC变化情况。当系统未采用所提模糊控制策略时,两电池组由于运行过程中充放电能量不均衡,在24～30 h间的每个充放电周期内,放电电池组A(B)因剩余容量不足,极易到达下一次充放电状态转换临界值,导致充电电池组B(A)未能充分充电,从而当下一阶段电池组B(A)执行放电任务时,剩余容量较少,又将较快进行电池组充放电状态转换。如此循环,以致在后阶段部分运行过程中(如33～35 h期间),两电池组剩余容量均严重不足,放电能力极弱。若此时为了平抑风电波动功率要求储能系统释放能量,则两组电池几乎都不工作,储能系统进入因放电能力不足的极端运行区间,难以保证长时间运行的可行性。而当采用所提模糊控制策略后,尽管不能保证每组电池始终在最佳放电深度下运行,但是通过实时优化两组电池的SOC,尽可能维持两电池组的充放电能力相当,避免了电池组因放电能力或充电能力不足而造成的极端运行情况。

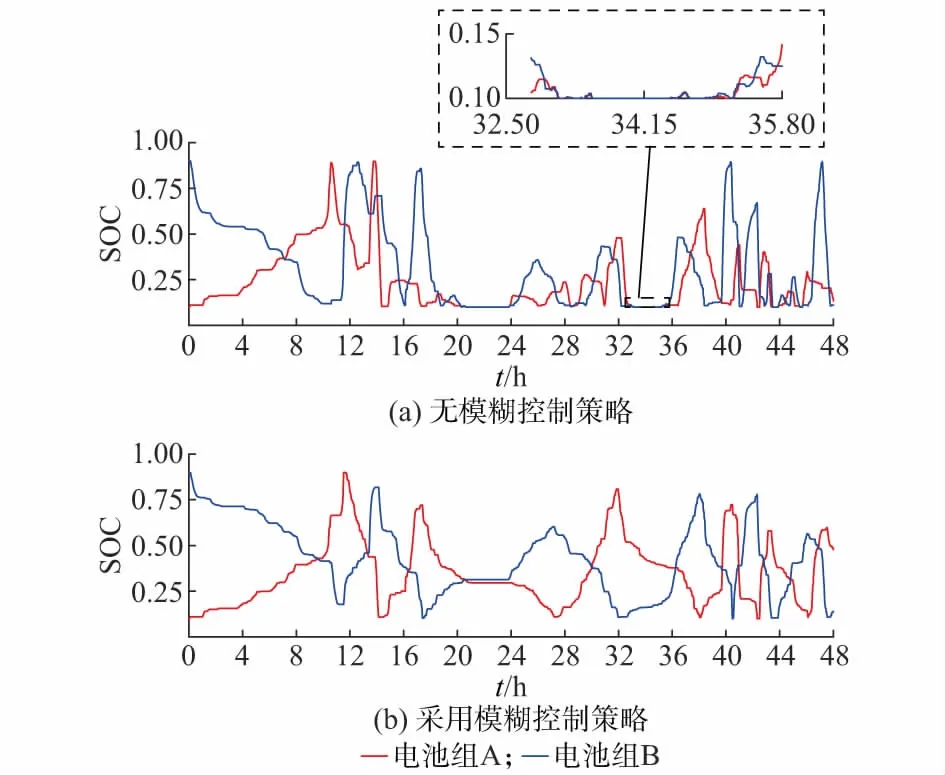
图3 有无模糊控制策略电池组A和电池组B的SOC曲线Fig.3 SOC curves of battery A and battery B with/without fuzzy control strategy

2)风电功率平抑效果分析

图4为有无采用所提模糊控制策略,风电波动功率的平抑效果图。分析图4可知,在仿真初始阶段(如4～5 h期间),有无模糊控制策略均能有效平滑风电波动功率,但相比之下,未采用模糊控制策略的平滑效果略优;而在部分运行期间(如34～35 h),不采用所提控制策略的DBESS对风电波动功率的平抑效果明显很差,甚至于完全丧失平抑能力。结合图3分析可知,当未采用控制策略时,在仿真运行某些期间,两电池组均过度放电,系统无法执行放电工作,难以满足平抑波动功率的能量需求。而采用所提模糊控制策略,由于优化了系统的运行状态,保证了系统在运行过程中的充放电能力相当,仅在极小部分区间(充放电状态转换附近)可能存在可充放电能力不足的情况,能有效满足平抑波动功率的需求。

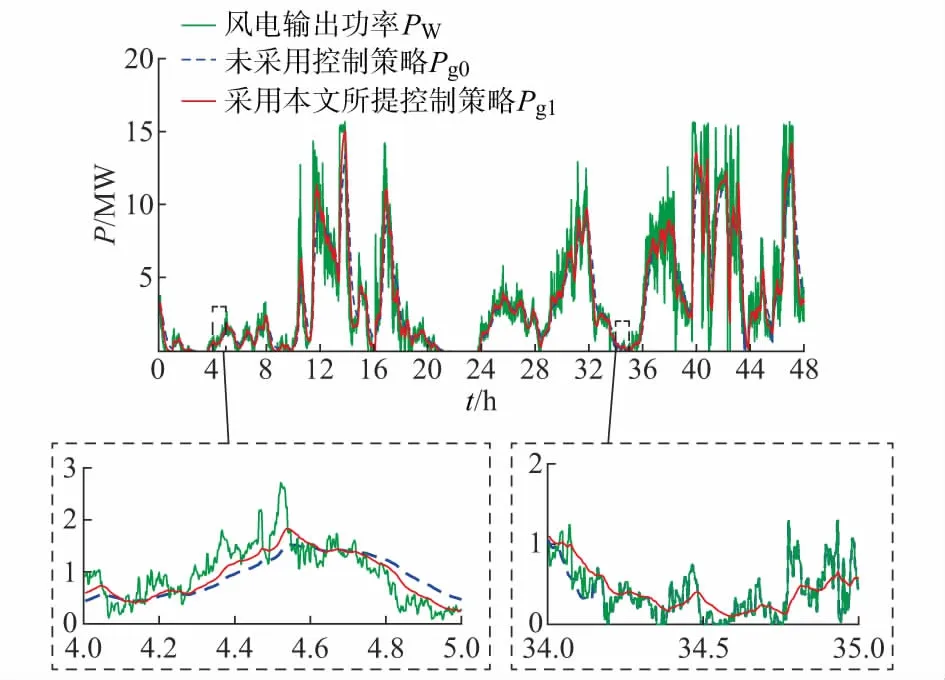
图4 风电输出功率Pw及有无模糊控制并网功率Pg1和Pg0Fig.4 Wind output power Pw and grid power Pg1/Pg0 with/without fuzzy control strategy

为了量化评估有无模糊控制策略对风电输出功率的平抑效果,对典型时间段(反映储能系统的充放电能力)的风电输出功率Pw、未采用模糊控制策略的风电并网功率Pg0和采用所提模糊控制策略的风电并网功率Pg1进行所提Rv指标计算,可得计算结果如表1所示。

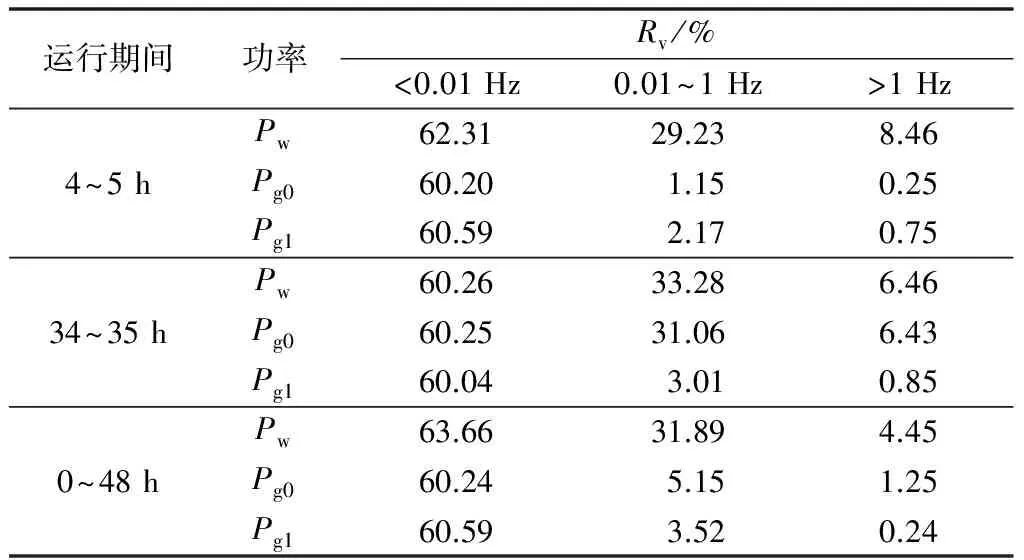
表1 不同情况下的Rv值Table 1 Value of Rv under different conditions

由表1可知,风电波动功率相对集中于低频段(小于0.01 Hz)与高频段(0.01～1 Hz),且因低频段的波动功率并网对电网的影响不大,DBESS主要平抑中高频段的风电波动功率。在4～5 h期间,DBESS可充放电容量充足,未采用控制策略并网功率Pg0中、高频段的Rv值分别为1.15%和0.25%,略优于采用模糊控制后Pg1的2.17%和0.75%,平抑效果较好。结合附录A图A5所示的采用模糊控制后0～5 h滤波时间常数变化情况可知,滤波时间常数在0～5 h的大部分期间都降低了,导致储能系统对风电波动功率的平滑效果略差。然而,在整个运行时间段(0～48 h),并网功率Pg0中、高频段的Rv值都略大于Pg1的Rv值,其原因主要在于未采用模糊控制策略时,DBESS在部分运行期间(如34～35 h)进入可放电能力不足的极端运行状态。此时,DBESS由于出力受限制,几乎无法释放能量以补偿波动功率缺额,对风电输出功率的平抑效果极差,进而影响整个仿真期间的平抑效果。

上述仿真计算结果较好地说明了所提模糊控制策略的有效性和正确性。

5 结语

本文考虑DBESS运行过程中的充放电能量不均衡,提出了表征系统运行状况的充放电饱和能力指标和充放电运行平稳度指标,并通过所设计模糊控制器实时修正一阶低通滤波器时间常数,优化控制两组电池的SOC。仿真结果表明,该方法使DBESS尽可能运行在给定最佳放电深度下,不仅避免了系统进入可充电能力或可放电能力不足的极端运行状况,确保储能系统长期稳定运行的可行性,还保证了储能系统对风电波动功率的平抑效果。由于本文理论研究的重点是保证DBESS长期稳定运行的平滑控制策略,而未深入研究系统容量配置不同对风电波动平滑效果的影响,这是本文后续需要进一步开展的工作。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] HAMEER S, NIEKERK J L. A review of large scale electrical energy storage[J]. International Journal of Energy Research, 2015, 39(9): 1179-1195.

[2] YE Y, SHI Y, TAY A. Electro-thermal cycle life model for lithium iron phosphate battery[J]. Journal of Power Sources, 2012, 217(11): 509-518.

[3] 严干贵,朱星旭,李军徽,等.内蕴运行寿命测算的混合储能系统控制策略设计[J].电力系统自动化,2013,37(1):110-114.

YAN Gangui, ZHU Xingxu, LI Junhui, et al. Control strategy design for hybrid energy storage system with intrinsic operation life measurement and calculation[J]. Automation of Electric Power Systems, 2013, 37(1): 110-114.

[4] 杨锡运,任杰,李相俊,等.储能系统平滑光伏电站功率波动的变参数斜率控制方法[J].电力系统自动化,2016,40(24):56-63.DOI:10.7500/AEPS20160129005.

YANG Xiyun, REN Jie, LI Xiangjun, et al. Slope control method with variable coefficients of battery energy storage system for smoothing photovoltaic power fluctuation[J]. Automation of Electric Power Systems, 2016, 40(24): 56-63. DOI: 10.7500/AEPS20160129005.

[5] 张峰,梁军,张利,等.考虑最佳期望输出与荷电状态的风电场储能容量优化方法[J].电力系统自动化,2014,38(24):12-19.DOI:10.7500/AEPS20131029002.

ZHANG Feng, LIANG Jun, ZHANG Li, et al. Energy storage capacity optimization for wind farms considering optimal expected output and SOC[J]. Automation of Electric Power Systems, 2014, 38(24): 12-19. DOI: 10.7500/AEPS20131029002.

[6] 李逢兵,谢开贵,张雪松,等.基于寿命量化的混合储能系统协调控制参数优化[J].电力系统自动化,2014,38(1):1-5.DOI:10.7500/AEPS20130503006.

LI Fengbing, XIE Kaigui, ZHANG Xuesong, et al. Optimization of coordinated control parameters for hybrid energy storage system based on life quantization[J]. Automation of Electric Power Systems, 2014, 38(1): 1-5. DOI: 10.7500/AEPS20130503006.

[7] 柴炜,李征,蔡旭,等.基于使用寿命模型的大容量电池储能系统变步长优化控制方法[J].电工技术学报,2016,31(14):58-66.

CAI Wei, LI Zheng, CAI Xu, et al. Variable step-size control method of large capacity battery energy storage system based on the life model[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 58-66.

[8] TRAN D, KHAMBADKONE A M. Energy management for lifetime extension of energy storage system in micro-grid applications[J]. IEEE Transactions on Smart Grid, 2013, 4(3):1289-1296.

[9] 李军徽,穆钢,崔新振,等.双锂电池-电容器混合储能系统控制策略设计[J].高电压技术,2015,41(10):3224-3232.

LI Junhui, MU Gang, CUI Xinzhen, et al. Control strategy design of dual lithium battery-capacitor hybrid energy storage system[J]. High Voltage Engineering, 2015, 41(10): 3224-3232.

[10] 李军徽,吉丽,崔新振,等.基于PSCAD/EMTDC的双电池组储能系统协调运行特性分析[J].电工技术学报,2015,30(14):434-441.

LI Junhui, JI Li, CUI Xinzhen, et al. Coordination operating characteristics analysis of dual battery energy storage system based on PSCAD/EMTDC[J]. Journal of Chinese Electrical Engineering Science, 2015, 30(14): 434-441.

[11] 张婳,张斌,籍天明,等.基于双向互补的储能系统控制策略及经济性分析[J].电力建设,2016,37(8):96-101.

ZHANG Hua, ZHANG Bin, JI Tianming, et al. Control strategy and economic analysis of energy storage system based on bidirectional complementary[J]. Electric Power Construction, 2016, 37(8): 96-101.

[12] YAO D L, CHOI S S, TSENG K J, et al. A Statistical approach to the design of a dispatchable wind power-battery energy storage system[J]. IEEE Transactions on Energy Conversion, 2009, 24(4): 916-925.

[13] YUAN Y, ZHANG X, JU P, et al. Applications of battery energy storage system for wind power dispatchability purpose[J]. Electric Power Systems Research, 2012, 93(10): 54-60.

[14] 李凯,马倩,徐红兵,等.储能系统的荷电状态管理策略及其影响评价[J].电力系统自动化,2015,39(8):27-32.DOI:10.7500/AEPS20140826008.

LI Kai, MA Qian, XU Hongbing, et al. SOC management strategy of storage system and its impact assessment[J]. Automation of Electric Power Systems, 2015, 39(8): 27-32. DOI: 10.7500/AEPS20140826008.