用于电力系统动态状态估计的改进鲁棒无迹卡尔曼滤波算法

曲正伟, 董一兵, 王云静, 陈 亮

(1. 电力电子节能与传动控制河北省重点实验室(燕山大学), 河北省秦皇岛市 066004;2. 国网河北省电力有限公司经济技术研究院, 河北省石家庄市 050024)

0 引言

近年来,智能电网态势感知逐渐成为研究热点[1-2],而电力系统状态估计是态势感知系统“理解”和“预测”的重要基础,也是能量管理系统的核心功能之一,对于系统调度、经济运行和实时控制起到了重要的作用。不同于静态状态估计,动态状态估计可以预测系统的运行趋势,得到了广泛应用[3]。动态状态估计主要以扩展卡尔曼滤波方法为主,但由于其需要计算雅可比矩阵,会产生线性化误差。为了解决这个问题,Julier提出了无迹卡尔曼滤波(unscented Kalman filter,UKF)算法,随后Vander Merwe对该方法进行了扩展,提出了平方根UKF方法[4]。但系统噪声的统计特性较难获得,为了改进UKF对于系统噪声的适应性,文献[5]提出了一种自适应无迹卡尔曼滤波(adaptive unscented Kalman filter,AUKF)算法,改进Sage-Husa噪声统计估值器,补偿系统噪声的影响。UKF算法的核心思想是无迹变换,最重要的就是Sigma点采样。目前最常用的采样方法是比例修正对称采样,在已有的状态估计模型中,常假设一些参数为定值,Sigma点的分布情况通常不变[6-9],但在某些高阶非线性系统中,参数为定值时估计性能较差[10]。

已有的状态估计模型通常都假设量测噪声是服从高斯分布的白噪声,在此条件下,可以获得对系统状态最优或次优的估计。然而实际的系统模型并不精确,而且噪声一般也不是高斯白噪声,往往存在量测粗差,增加了系统的不确定性,估计性能难以得到保证。鉴于系统中的不良数据会对状态估计结果造成很大影响,人们提出了抗差状态估计,主要包括加权最小绝对值、二次线性估计及二次常数估计等。可以在估计过程中自动抑制不良数据[11]。近年来又提出了许多改进方法[12],包括以合格率最大为目标的状态估计[13-16]、指数型目标函数状态估计[17-18]、最大指数绝对值状态估计[19],以及量测噪声自适应抗差状态估计[20]。

上述方法在存在不良数据的情况下,有较好的估计效果,但当系统中没有不良数据时,估计效果往往不如原始算法[21]。针对以上不足,本文提出一种改进鲁棒无迹卡尔曼滤波(robust unscented Kalman filter,RUKF)状态估计算法。首先改进传统的UKF算法,通过调节比例修正因子实时调整Sigma采样点的分布来保证估计精度;给出粗差判据,通过增强因子对系统量测噪声进行修正,仿真验证了本文算法的有效性。

1 动态状态估计概述

1.1 动态状态估计模型

非线性系统状态方程和量测方程可用如下形式表示:

xk=f(xk-1)+qk-1

(1)

yk=h(xk)+rk

(2)

式中:xk为n维状态矢量;yk为m维量测矢量;f(·)为k-1时刻的状态转移函数矢量;h(·)为量测函数矢量,量测模型采用混合量测;qk～N(0,Qk)为系统误差;rk+1～N(0,Rk+1)为量测误差。状态方程采用两参数指数平滑法[22]。

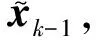
(3)

式中:ak-1和bk-1为中间变量;αH和βH为平滑参数,通常取值为[0,1]。

1.2 UKF算法原理

UKF算法是基于卡尔曼滤波框架,通过无损变换(UT)模拟非线性函数的概率密度达到近似效果,基本原理是以状态量均值点为中心,使用一组带有权重的Sigma点近似非线性函数随机分布,将点集中的所有点非线性变换,最后加权求和,得到状态量和方差。

1.2.1UT过程

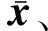
(4)

(5)

式中:L为Sigma点的个数。

2)对所有Sigma点集进行非线性变换,得到变换后的点集Yi=g(χi)。

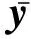
(6)

(7)

1.2.2预测

根据k-1时刻的状态量xk-1和协方差Pk-1,根据选取的采样策略构造Sigma点集χi,k-1,得到k时刻的统计量为:

χi,k|k-1=f(χi,k-1)+qk-1

(8)

(9)

(10)

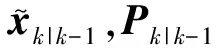
(11)

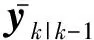
(12)

(13)

(14)

1.2.3更新

计算增益Kk、k时刻状态估计值xk和协方差估计值Pk:

(15)

(16)

(17)

2 RUKF动态状态估计

2.1 改进UKF算法

采用对称采样确定Sigma点集,其比例修正原理如下[9]:

(18)

λ=α2(n+κ)-n

(19)

均值和方差的权值为:

(20)

(21)

(22)

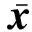
Sigma点集能否捕捉高阶矩阵的信息对于状态估计性能有很大的影响。在实际应用中,κ,α和β常常取为定值,Sigma点的分布情况不变,但这种情况的估计性能较差,尤其是在高阶非线性系统中。为了解决这个问题,希望能够根据高阶矩阵的先验分布来实时调节Sigma点到均值的距离,其中α决定均值周围Sigma点的分布状态,通过调节α值,使高阶项的影响达到最小。具体方法如下。

将式(19)代入式(18)得到:

(23)

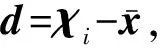
(24)

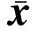
(25)

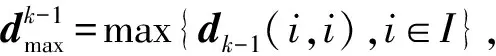
(26)

再将αk代入式(23)重新进行采样确定Sigma点集,进入下一时刻估计,如此进行改进UKF算法的动态状态估计。

2.2 RUKF算法

在改进UKF状态估计中,系统量测粗差会引起卡尔曼滤波框架下的滤波器滤波性能下降或发散。本文提出一种RUKF算法,以解决系统所具有的不确定性,消除粗差的影响。

(27)

其中,残差ηk及观测量自协方差Sk分别为

(28)

(29)

当系统出现量测粗差时,残差协方差矩阵的理论值和实际值不再满足式(27),此时引入增强因子φk,使式(27)重新匹配,即

Pηk=Sk+φkRk

(30)

这样,式(15)的增益矩阵变为:

Kk=Ck(Sk+φkRk)-1

(31)

根据式(31)进行测量更新。

增强因子φk可通过下式求解,对式(27)两边求迹,有

(32)

(33)

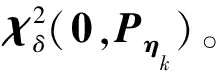
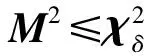
3 基于RUKF算法的电力系统状态估计流程

基于RUKF算法的电力系统状态估计流程如图1所示。

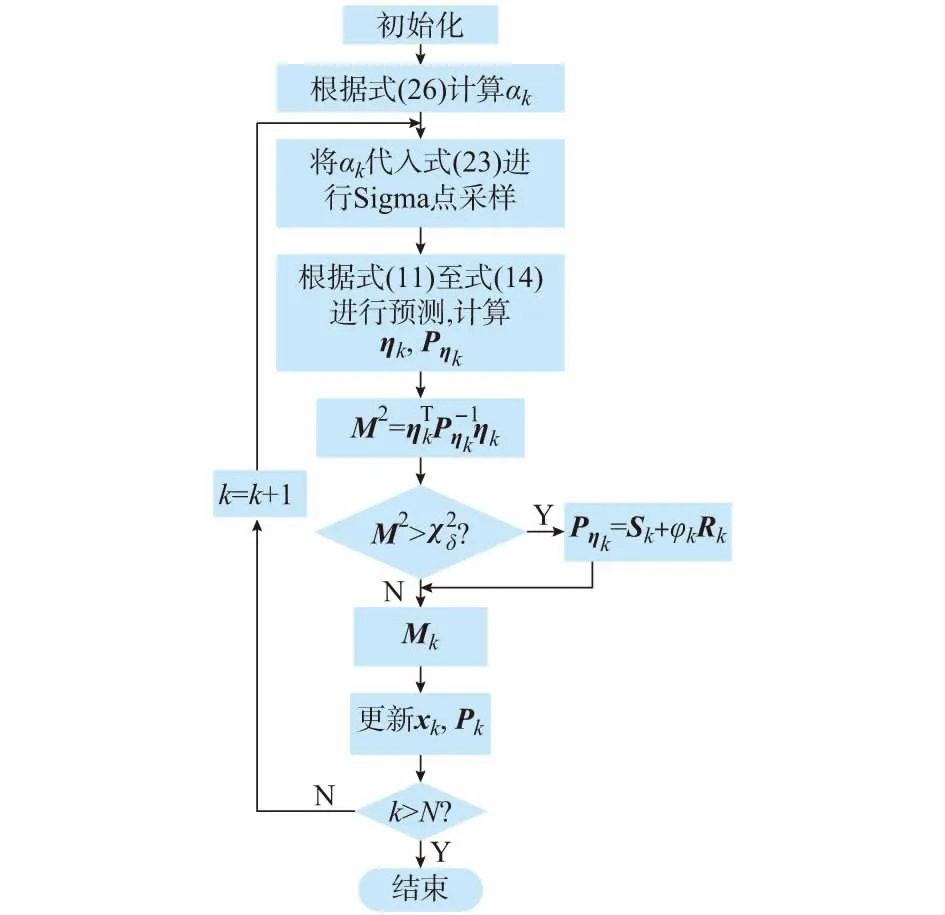
图1 RUKF状态估计流程Fig.1 Flow chart of RUKF state estimation

状态量xk=[Vk,θk]∈Rn为节点电压幅值和相角,量测量yk=[Pk,Qk,Vk,θk]T∈Rm为节点的有功功率、无功功率、电压幅值和相角。对于节点i,yk可表示如下:

(34)

具体步骤如下。

1)初始化。根据两参数指数平滑法,选取前两个时刻的状态量为真值,状态量的协方差和系统误差的协方差初值均假设为量测误差的协方差矩阵。根据式(26)计算αk。

2)预测。将αk代入式(23)根据对称采样策略获得采样点,按照式(11)至式(14)预测日下一时刻的状态量和方差,并计算ηk和Pηk。

3)更新。根据式(15)至式(17),得到下一时刻的状态量和方差。

4 算例分析

使用均方根误差(root mean square error,RMSE)作为性能指标函数。k时刻的均方根误差公式为:

(35)

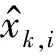
以IEEE 30节点标准测试系统为例,对本文所提RUKF算法进行验证。负荷使用某电网系统的日负荷统计数据,每10 min采集一次,一日24 h共144个采样点,通过潮流计算获得状态量的真实值,加上服从高斯分布的随机扰动作为量测量。数据采集与监控(SCADA)量测系统的误差标准差为0.02,均值为0;相量测量单元(PMU)电压幅值量测误差标准差为0.005,均值为0,PMU电压相角量测误差标准差为0.002,均值为0,PMU的配置点为1,7,15,17,19,24,27,30[23]。其中,α=1,κ=0,β=2。其动态模型采用Holt两参数法,两参数法的取值为αH=0.85,βH=0.05。

首先验证的是改进UKF算法,其仿真结果如附录A图A1所示,均方根误差如表1所示。

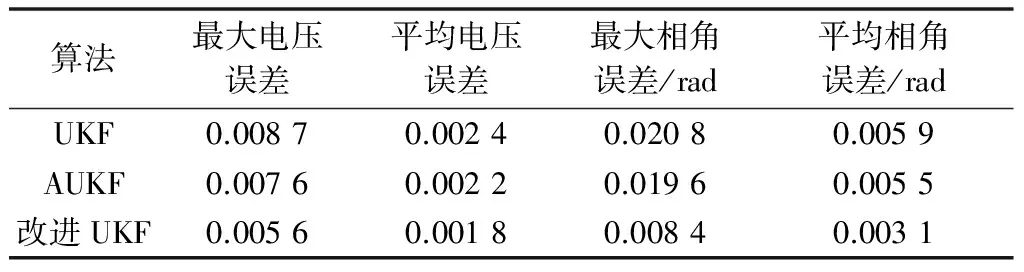
表1 均方根误差比较Table 1 Comparison of root mean square errors

由仿真结果看出,改进UKF算法较AUKF和UKF算法误差相对较小,更加接近真实值。这是由于改进UKF算法可以实时调节比例修正因子,捕捉高阶矩阵的信息,避免了α取为定值的缺陷。因此,改进UKF算法更加适应系统模型,具有更高的估计精度。

附录A图A2给出了各时刻比例修正因子的值。可以看出,α不是一个定值,而是在每次估计中都被自动调节,并最终趋于一个定值,精度误差为10-3,这样避免了α取为定值时,因取值不当造成的估计性能下降,从而增强了模型的适应性,提高了算法的估计精度。

为了验证RUKF算法的抗差性与鲁棒性,比较UKF、改进UKF和RUKF三种算法的估计效果。量测粗差通过扩大量测量方式获得,在上述IEEE 30节点系统中,在k=50时刻,将节点10的电压幅值扩大100倍,仿真结果见附录A图A3,均方根误差如表2所示。

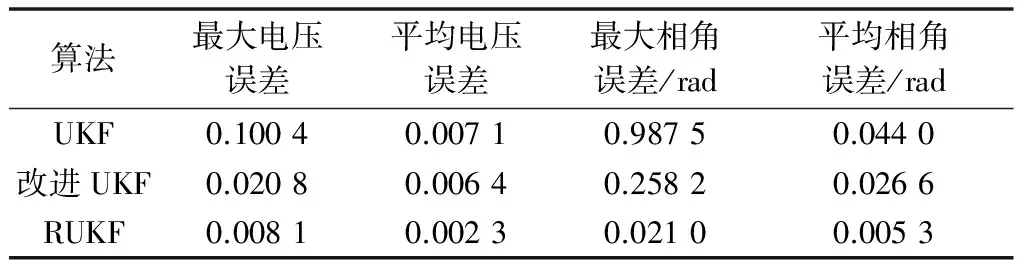
表2 IEEE 30节点系统存在粗差时的均方根误差比较Table 2 Comparison of root mean square errors with gross error of IEEE 30-bus system

可以看出,当系统中存在粗差时,UKF算法和改进UKF算法并没有消除粗差的影响,它们所估计出来的值偏离真实值较大。改进UKF算法较UKF算法误差较小,进一步说明改进UKF算法具有较好的估计性能,而RUKF算法则未受到测量粗差的影响,估计效果最好。

为进一步验证RUKF算法对不同比例粗差的抗差效果,在IEEE 30节点系统上分别进行30次独立试验,每次试验在全量测中构造的粗差比例为0%～5%,粗差通过量测量扩大10倍获得,并统计30次试验的最大误差和平均误差。

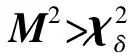
为了验证RUKF算法在大规模系统中的估计精度和计算效率,在同样的运行条件下,在IEEE 118节点系统中将量测量扩大10倍,取粗差比例为5%,仿真结果如附录B表B1和表B2所示。可见,对于大规模系统,本文算法可以有效降低估计误差,估计性能优于UKF算法和改进UKF算法,而运行时间相差不大,对于大规模系统可满足实时性要求。

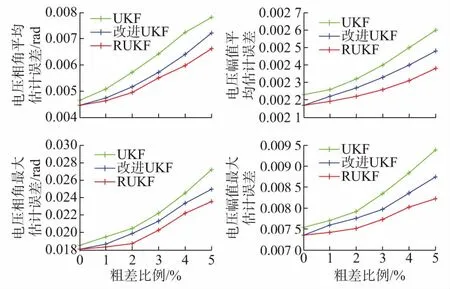
图2 不同粗差比例下三种算法的误差比较Fig.2 Error comparison of three algorithms under different gross error ratios

5 结语

本文提出了一种RUKF算法,并将其应用于电力系统状态估计,该方法克服了传统UKF算法比例修正因子取为定值的缺陷,提高了估计精度。引入了粗差判据,当系统存在粗差时,通过增强因子可以降低量测值的权重,从而有效降低粗差对状态估计结果的影响,使估计结果更接近真实值。

不良数据的检测与辨识是电力系统状态估计的一项重要工作。本文提出的RUKF算法只针对粗差的检测,并不能辨识出粗差,下一步的研究方向将是粗差的辨识。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 周华锋,胡荣,李晓露,等.基于态势感知技术的电力系统运行驾驶舱设计[J].电力系统自动化,2015,39(7):130-136.DOI:10.7500/AEPS20140809003.

ZHOU Huafeng, HU Rong, LI Xiaolu, et al. Design of power system operation cockpit based on situation awareness technology[J]. Automation of Electric Power Systems, 2015, 39(7): 130-136. DOI: 10.7500/AEPS20140809003.

[2] 王守相,梁栋,葛磊蛟.智能配电网态势感知和态势利导关键技术[J].电力系统自动化,2016,40(12):2-8.DOI:10.7500/AEPS20160509003.

WANG Shouxiang, LIANG Dong, GE Leijiao. Key technologies of situation awareness and orientation for smart distribution system[J]. Automation of Electric Power Systems, 2016, 40(12): 2-8. DOI: 10.7500/AEPS20160509003.

[3] 于尔铿.电力系统状态估计[M].北京:水利电力出版社,1985.

[4] 卫志农,孙国强,庞博.无迹卡尔曼滤波及其平方根形式在电力系统动态状态估计中的应用[J].中国电机工程学报,2011,31(16):74-80.

WEI Zhinong, SUN Guoqiang, PANG Bo. Application of UKF and SRUKF to power system dynamic state estimation[J]. Proceedings of the CSEE, 2011, 31(16): 74-80.

[5] 赵洪山,田甜.基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J].电网技术,2014,38(1):188-192.

ZHAO Hongshan, TIAN Tian. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Tecnology, 2014, 38(1): 188-192.

[6] 李大路,李蕊,孙元章.混合量测下基于UKF的电力系统动态状态估计[J].电力系统自动化,2010,34(17):17-21.

LI Dalu, LI Rui, SUN Yuanzhang. Power system dynamic state estimation with mixed measurements based on UKF [J]. Automation of Electric Power Systems, 2010, 34(17): 17-21.

[7] 孙国强,黄蔓云,卫志农,等.基于无迹变换强跟踪滤波的发电机动态状态估计[J].中国电机工程学报,2016,36(3):615-623.

SUN Guoqiang, HUANG Manyun, WEI Zhinong, et al. Dynamic state estimation for synchronous machines based on unscented transformation of strong tracking filter[J]. Proceedings of the CSEE, 2016, 36(3): 615-623.

[8] LIN Yangping, LIU Kaizhou, WANG Liuxian. An adaptive square-root unscented Kalman filter for underwater vehicle navigation[C]// International Conference on Mechatronics and Automation, August 3-6, 2014, Tianjin, China: 717-722.

[9] JULIER S J. The scaled unscented transformation[C]// Proceedings of the 2002 American Control Conference, May 8-10, 2002, Anchorage, AK, USA: 4555-4559.

[10] NIE Yongfang, TAO Zhang. A self-adaptive scaling parameter selection algorithm for the unscented Kalman filter[C]// Chinese Automation Congress, November 27-29, 2015, Wuhan, China: 86-90.

[11] 李碧君,薛禹胜,顾锦汶,等.抗差估计及其在电力系统中的应用[J].电力系统自动化,1999,23(1):56-60.

LI Bijun, XUE Yusheng, GU Jinwen, et al. Robust estimation theory and its application in power system[J]. Automation of Electric Power Systems, 1999, 23(1): 56-60.

[12] 厉超,卫志农,倪明,等.基于变量代换内点法的加权最小绝对值抗差状态估计[J].电力系统自动化,2015,39(6):48-52.DOI:10.7500/AEPS20140328013.

LI Chao, WEI Zhinong, NI Ming, et al. WLAV robust state estimation based on variable substitution interior point method[J]. Automation of Electric Power Systems, 2015, 39(6): 48-52. DOI: 10.7500/AEPS20140328013.

[13] 董树锋,何光宇,孙英云,等.以合格率最大为目标的电力系统状态估计新方法[J].电力系统自动化,2009,33(16):40-43.

DONG Shufeng, HE Guangyu, SUN Yingyun, et al. A novel method for power system state estimation with maximum good measure rate[J]. Automation of Electric Power Systems, 2009, 33(16): 40-43.

[14] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(一)结果评价[J].电力系统自动化,2009,33(19):21-24.

HE Guangyu, DONG Shufeng. Power system static state estimation based on uncertainty of measurement: Part one result evaluation[J]. Automation of Electric Power Systems, 2009, 33(19): 21-24.

[15] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(二)方法研究[J].电力系统自动化,2009,33(20):32-36.

HE Guangyu, DONG Shufeng. Power system static state estimation based on uncertainty of measurement: Part two a new method[J]. Automation of Electric Power Systems, 2009, 33(20): 32-36.

[16] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(三)算法比较[J].电力系统自动化,2009,33(21):28-31.

HE Guangyu, DONG Shufeng. Power system static state estimation based on uncertainty of measurement: Part three algorithms compared[J]. Automation of Electric Power Systems, 2009, 33(21): 28-31.

[17] 姚诸香,郭烨,郭玉金,等.含指数型目标函数的电力系统抗差状态估计方法在江西电网中的应用[J].中国电机工程学报,2012,36(4):155-159.

YAO Zhuxiang, GUO Ye, GUO Jinyu, et al. Application of a robust state estimator based on maximum exponential square in Jiangxi power system[J]. Proceedings of the CSEE, 2012, 36(4): 155-159.

[18] 郭烨,张伯明,吴文传.指数型目标函数电力系统抗差状态估计的解法与性能分析[J].中国电机工程学报,2011,31(7):89-95.

GUO Ye, ZHANG Boming, WU Wenchuan. Solution and performance analysis to a robust state estimation method with exponential objective function[J]. Proceedings of the CSEE, 2011, 31(7): 89-95.

[19] 付艳兰,陈艳波,姚锐,等.基于最大指数绝对值目标函数的抗差状态估计方法[J].电网技术,2013,37(11):3166-3171.

FU Yanlan, CHEN Yanbo, YAO Rui, et al. A robust state estimation approach based on objective function of maximum exponential absolute value[J]. Power System Technology, 2013, 37(11): 3166-3171.

[20] 陈艳波,马进,文一宇.一种电力系统量测噪声自适应抗差状态估计方法[J].电力系统自动化,2015,39(8):66-73.DOI:10.7500/AEPS20140402006.

CHEN Yanbo, MA Jin, WEN Yiyu. An adaptive robust state estimation approach for measurement noise[J]. Automation of Electric Power Systems, 2015, 39(8): 66-73. DOI: 10.7500/AEPS20140402006.

[21] 陈艳波,马进.一种双线性抗差状态估计方法[J].电力系统自动化,2015,39(6):41-47.DOI:10.7500/AEPS20140410009.

CHEN Yanbo, MA Jin. A bilinear robust state estimation method for power systems[J]. Automation of Electric Power Systems, 2015, 39(6): 41-47. DOI: 10.7500/AEPS20140410009.

[22] 贺觅知.基于卡尔曼滤波的电力系统动态状态估计算法研究[D].成都:西南交通大学,2006.

[23] 周琦.基于PMU优化的电力系统状态估计算法的研究[D].保定:华北电力大学,2008.