三相不平衡配电网不确定性分布式电源运行域仿射求解算法

吴在军, 胡靖宜, 李培帅, 王 洋, 窦晓波, 胡敏强

(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 国网江苏省电力公司经济技术研究院, 江苏省南京市 210008)

0 引言

具有波动性和间歇性的分布式电源(DG)如果不加以合理调控,将导致DG高渗透的配电网电压频繁波动,过电压与欠电压问题恶化,运行损耗变高,严重时甚至导致DG退出运行[1-3],限制DG渗透率的提高。定量分析DG对网络的影响,在保证安全稳定前提下尽可能多地接入DG是解决上述问题的有效办法[4]。

传统关于DG接入容量的研究主要集中在求解最佳接入方式下DG的最大接入容量[5]。此类研究主要为DG接入配电网的规划选址提供参考,但在实际运行阶段,一旦DG接入的位置或容量改变,网络约束难以保证[6]。为应对运行阶段DG接入带来的挑战,文献[7]和文献[8]分别研究了电力系统潮流可行域边界的拓扑性质并给出了计算方法,分析表明DG注入空间的潮流可行域具有超平面的几何特征。其所述的潮流可行域能够保证潮流方程有解,但未考虑系统安全运行约束。

文献[9]提出了配电系统安全域体积的概念与求解算法,但未将DG接入对配电网的影响考虑在内。文献[10]提出了一种考虑N-1安全约束的DG出力控制可视化方法,但假设条件适用范围有限,且仅对风电和光伏机组组合出力上限进行求解,无法得到整个域的边界信息。文献[11]针对有源配电网提出了全象限配电系统安全域的概念与模型,研究场景假定配电网和DG均具备足够的调压能力,故模型中不含电压约束条件。文献[12]考虑配电网多为辐射状网络,不具备N-1后的负荷转移能力,提出了保证配电网N-0安全的DG运行域的概念并将其可视化,但其计算方法属于仿真逼近法,即在网络拓扑确定的条件下,计算在各种负荷水平下的电压分布和系统短路电流,逐渐增大DG出力,重复计算直到满足临界条件。该方法在步长足够小的情况下,结果准确,但计算效率较低,且难以应用于优化模型中作为约束条件。此外,以上方法均没有对三相不平衡系统进行建模,而配电网多为三相不平衡的系统。

本文针对三相不平衡配电网提出一种基于仿射算术的DG运行域求解方法。通过线性近似仿射潮流计算节点电压关于DG出力的定量表达式,综合考虑电压安全范围、馈线容量和反向潮流等约束条件,得到配电网中多个DG 的完整运行域。该方法可用于计算恒功率因数DG、PQ型DG、负荷的运行域,以及这几类的组合运行域。与仿真逼近法相比,该方法基于优化模型进行求解,计算效率高、适用性广,且其约束条件可扩展应用于其他优化领域。

1 基于仿射算法的近似线性化潮流

仿射算法可以在整个计算过程中跟踪变量的相关性并且限制对潮流运算结果范围的过大估计[13-14]。本文将仿射算法代入适用于三相不平衡配电网的线性近似潮流算法[15]中,定量分析各节点电压与各DG出力波动量的关系,得到节点电压关于DG波动量的仿射线性表达式。

1.1 三相不平衡配电网潮流模型

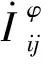
(1)

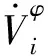
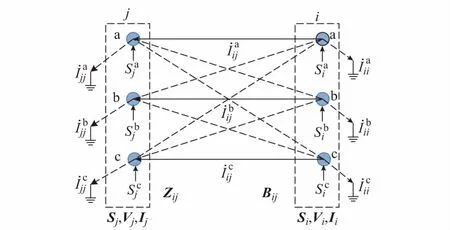
图1 三相线路π形等效电路Fig.1 π-shape equivalent circuit of three-phase line

支路(i,j)各电气量满足如下关系:

(2)

(3)

式中:*表示其共轭值,下同。

根据基尔霍夫电流定律可得:

(4)

对于三相运行线路,令yij=(Zij)-1;对于两相运行的线路(如a,b两相),其等效电路参数如下:

(5)

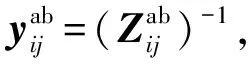
(6)

对于一相单独运行的线路(如a相),其等效电路参数如下:

(7)

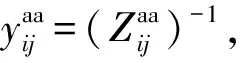
(8)

由式(1)和式(4) 可得:

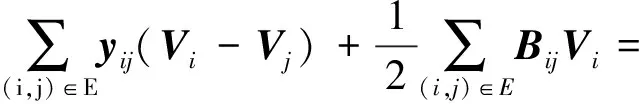
(9)

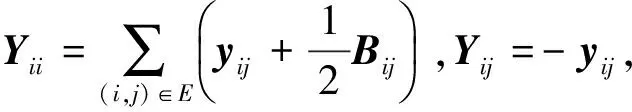
(10)

式中:Yij和Yii均为3×3 阶矩阵。

整个电网的节点电压与注入电流的关系满足如下等式:

(11)

三相潮流方程如下:

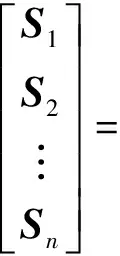
(12)

1.2 线性化潮流模型

任意电力网络中,其节点注入电流与节点电压之间满足如下关系[15]:

(13)

式中:S为松弛节点编号;N为除松弛节点外其他节点集合。

节点注入电流为:

(14)

(15)

忽略高阶项,可得线性近似形式如下:

(16)

将式(16)代入式(14)中,可将节点注入电流近似为如下线性形式:

(17)

1.3 DG出力的仿射形式

各DG出力均以区间量的形式给出。

设接于节点i的φ相DG有功输出为:

(18)

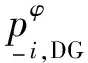
对于任意DG,其有功、无功出力需满足如下约束:

(19)

为分析各节点电压与各DG出力之间的定量关系,将DG有功、无功出力转化为仿射形式:

(20)

(21)

(22)

(23)

式中:εP,i和εQ,i分别为DG有功、无功出力的噪声元。

由此可知,DG的有功、无功出力可表示为确定量与波动量之和的形式。

1.4 节点电压关于DG波动量的仿射表达式

三相不平衡配电网中,某节点的注入功率仿射形式为[17]:

(24)

(25)

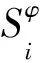
根据DG出力的仿射形式,三相不平衡配电网中任意节点的注入功率均可表示为确定量与波动量之和的形式:

(26)

(27)

(28)

(29)

将式(29)代入式(13)并写为紧凑形式:

D+E-F(ΔVN)*+G=YNNVN,0+YNNΔVN

(30)

D=-YNSVS+(SN,0./VN,0)*

(31)

E=(ΔSN./VN,0)*

(32)

F=diag((SN,0./(VN,0.×VN,0))*)

(33)

G=-[(ΔSN.×ΔVN)./(VN,0.×VN,0)]*

(34)

式中:./和.×分别表示矩阵元素相除和相乘。

VN,0为确定性潮流解,因此有:

D=YNNVN,0

(35)

E-F(ΔVN)*+G=YNNΔVN

(36)

将ΔVN分成如下两部分:

ΔVN=ΔVN1+ΔVN2

(37)

式中:ΔVN1为节点电压一阶波动量;ΔVN2为节点电压非线性波动量。

由式(36)可得到如下两组方程:

YNNΔVN1+F(ΔVN1)*=E

(38)

YNNΔVN2+F(ΔVN2)*=G

(39)

求解式(38)和式(39)所示的两组方程,可得到节点电压的一阶波动量ΔVN1和非线性波动量ΔVN2,通过确定性潮流计算可得到满足式(35)的节点电压确定性分量VN,0。三者求和即为节点电压的仿射表达形式。

将式(38)和式(39)的实部、虚部展开得到:

(40)

(41)

(42)

式中:下标re和im分别表示相应量的实部和虚部。

根据式(29)、式(30) 和式(32),向量E中的元素为:

(43)

而H为一个常数阵,因此通过式(38)可求得节点电压的一阶波动量ΔVN1,并保持如下仿射形式:

(44)

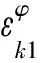
求得VN,0和ΔVN1后,通过式(39)可求解非线性波动量ΔVN2。为避免式(39)中的非线性仿射运算,需要进行迭代求解。根据式(25)和式(34),向量G中的元素为:

(45)

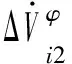
(46)

根据文献[18]中所述仿射乘法运算规则及式(43)至式(46),得到:

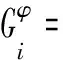
(47)

交替迭代式(41)和式(46),即可求得节点电压的非线性波动量ΔVN2,其值也保持式(46)的仿射形式。最终三者求和即得到节点电压的复仿射形式。

通过解耦将节点电压的确定量、线性波动量和非线性波动量分别计算,使得在求解节点电压确定量和一阶波动量的过程中,仅含有线性仿射运算,不会造成求解区间扩大;在求解非线性波动量的过程中,仅涉及少量的仿射乘法运算。因此,相比较于一般算法,该方法求解精度更高,保守性更好,为下文精确计算运行域奠定基础。

2 基于近似线性化潮流的DG运行域求解

2.1 约束条件线性化

将DG有功、无功出力仿射量代入上一部分的求解中可以得到节点电压关于DG出力波动量的线性关系。此过程中含有DG出力的不等式约束和潮流等式约束。忽略节点电压非线性波动量ΔVN2,可获得各节点电压复向量的仿射表达式为:

(48)

即节点电压复向量为关于εP和εQ的线性函数,则节点电压需满足如下约束:

(49)

式中:Umax和Umin分别为安全节点电压幅值的上、下限。

上述约束在复平面里构成了一个以零点为圆心,分别以Umin,Umax为半径的圆环,用正十二边形可对电压上界的约束条件进行线性近似,见附录A图A1。

电压下界约束则采用灵敏度法将其线性化,如式(50)所示[17]。

(50)

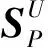
由此约束条件转化为关于εP,εQ的线性不等式,其中隐含了关于系统潮流、DG出力和电压偏移的约束条件,求解方便。

此外,在约束条件中再增加馈线容量约束和反向潮流约束如下:

L≤Lmax

(51)

L1≥0

(52)

式中:Lmax为馈线额定容量;L为馈线容量;L1为馈线出口处的线路容量。式(52)表示馈线出口潮流不反向。

2.2 运行域边界求解

为将运行域可视化,给出二维空间上的运行域边界可视化的求解步骤,即除2个研究的负荷或DG工作点为变量外,其余节点负荷或DG情况均保持不变,通过仿真拟合方法计算负荷或DG运行域边界。

任意选取2个工作点,分析工作点的运行域边界,算法流程如图2所示。

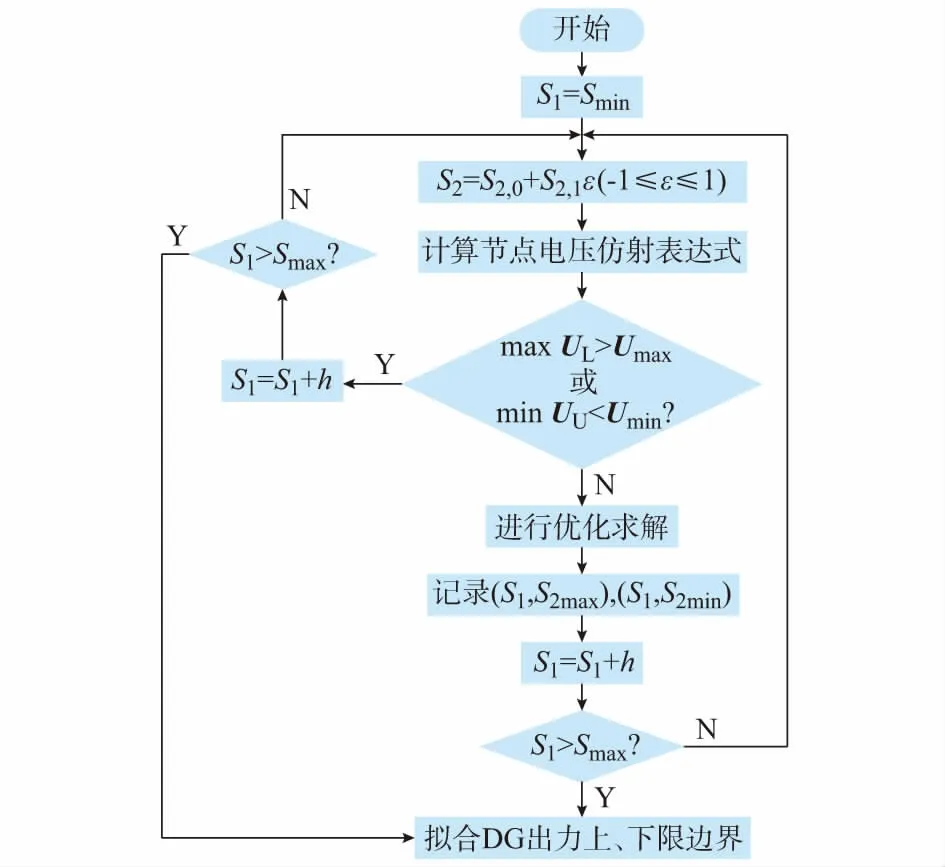
图2 运行域边界求解流程图Fig.2 Flow chart of solution of dispatchable region boundary

图中:S1和S2分别为2个工作点出力大小,将S2的出力区间表示为仿射形式;Smax和Smin分别为DG的最大和最小出力;UU和UL分别为由关于DG波动量的电压表达式计算得到的电压幅值最大、最小值矩阵;S2max和S2min分别为优化求解得到的S2最大和最小出力;h为步长。

首先,对每个二维断面,利用电压约束求出一系列临界工作点,具体如下。

1)在DG出力范围内,对2 个工作点的其中一个S1从最小出力值开始,以一定步长取一系列值;另一个工作点S2将出力范围按式(20)至式(23)用仿射数表示。

2)对于S1每个值,按照本文1.4节所述计算节点电压仿射表达式,得到各节点电压与各DG波动量的定量关系,通过表达式计算出节点电压幅值的最值并与安全电压上下限进行比较,判断是否进行优化求解。

3)若判断满足条件,则将上一步骤中得到的各节点电压与各DG的等量关系代入优化求解模型中求解,模型如下:

(53)

其中约束条件可按2.1节中的方法进行线性化,然后求解优化模型得到S1一定时的S2的最大、最小值。高维度的运行域可由式(53)中的约束条件线性化后的一组线性不等式来表示。

4)利用所得出的一系列功率最值,即可拟合成负荷或DG的运行域边界。

3 算例验证

本文以改进的IEEE 123节点三相不平衡系统为例,验证所提出的高不确定性DG运行域的仿射求解算法,并与文献[14]提出的仿真逼近式的求解方法进行对比分析,以验证本文模型的求解精度和效率。仿真程序在MATLAB平台上编制,算例中的优化问题采用YALMIP 建模,并采用CPLEX 求解。

3.1 测试系统

改进的IEEE 123节点三相不对称配电系统,其网络结构见附录B图B1,电压等级为4.16 kV,根节点电压幅值设定为1.05(标幺值),馈线额定容量为5.28 MW,三相负荷总有功率为3 490 kW,总无功功率为1 925 kvar,系统三相不平衡普遍存在,各相所带有功负荷差最大达到数百千瓦。另外该系统中存在众多自阻抗及互阻为零,以单相运行或者两相运行的支路的线路参数也存在严重的三相不对称,数值条件复杂。本文在原系统的基础上接入DG进行验证。

3.2 含DG的配电网电压幅值分析

当DG的波动范围比较大时,会导致节点电压出现越限,通过本文所述的方法可以求解负荷或DG的运行域,保证运行域中的工作点电压在安全范围内(0.95～1.05)且馈线容量和反向潮流均满足要求。在该测试系统中的节点27的C相、节点65的B相、节点101的A相分别接入三个单相DG,节点47 和节点114 分别接入两个三相DG。每个DG的有功出力均具有不确定性,在其额定功率附近有±50%的波动,具体DG的接入信息见附录B表B1。

按照本文方法计算节点电压仿射表达式的最大、最小值,并与蒙特卡洛仿真(MCS)求解得到的节点电压幅值进行对比,结果见附录C图C1。

当DG出力不加以控制时,三相中均有部分节点的幅值在红线以外,出现了电压幅值越界的情况。因此,分析计算DG的运行域对保证系统安全和电能质量具有重要意义。

当系统含有n个波动性DG时,运行域与这n个DG的波动均相关,每一个线性约束条件的边界构成一个超平面,基于多个超平面形成的运行域表现出多面体的几何特征。算例含有9个波动的DG,因此此时DG的运行域为一个9维的多面体,难以可视化。为了使运行域可视化,本文采用一维、二维运行域进行表示,即仅含有1个或2个的负荷或DG变量。

3.3 系统负荷运行域

不加入任何DG,仅考虑负荷波动,分析系统的负荷运行域。在附录B图B1的系统结构中,当节点27的C相处接入负荷为-400 kW时,节点47的A相处负荷波动最大范围为-400～-200 kW,得出节点47的A相处的一维负荷运行域,并用仿真逼近法所得到的近似精确解进行验证,结果如附录D表D1所示。将负荷运行域的最大相对误差定义为:

(54)

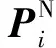
由附录D表D1可知,本文所提出的算法具有良好的求解精度。由于忽略了高阶波动量,计算中会产生一定的误差。但最大相对误差不超过1%,可满足大部分的应用场合。

当节点27的C相与节点47的A相处均为波动负荷时,波动的最大范围为-400～-200 kW,可得到关于这两节点的二维负荷运行域,与近似精确解进行对比验证,结果如图3所示。图中:P47和P27分别为节点47和节点27的负荷有功功率。

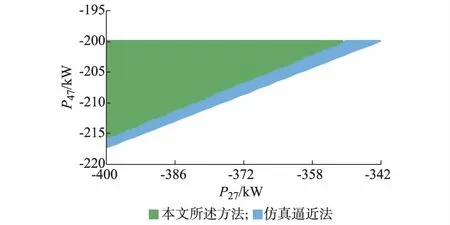
图3 负荷的二维运行域Fig.3 Two-dimensional dispatchable region of load

由图3可以看出,对于改进的IEEE 123系统,节点47的A相相较于节点27的C相的波动对电压的影响更大,故而运行域的范围也更小。图3中蓝色区域为仿真逼近法所得到的近似精确负荷二维运行域,绿色区域为本文所述方法所得到的运行域,绿色区域均在蓝色区域内,说明了本文所述算法的准确性。此外,负荷运行域的误差值均保证在一个相对稳定的范围内,不存在误差的积累,故该算法也具有较好的稳定性。

3.4 恒功率因数DG运行域

在节点27的C相以及节点47的A相分别安装波动性DG,出力的波动范围均为300～500 kW,且该DG均以恒功率因数模式运行,功率因数为0.9。确保配电网各节点电压均在安全范围内,利用上述方法求取该系统中恒功率因数运行DG的运行域,结果如图4所示。

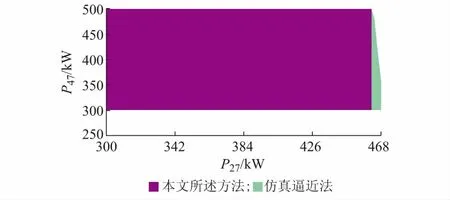
图4 二维恒功率因数DG运行域Fig.4 Two-dimensional dispatchable region of DG with constant power factor

图4中紫色区域表示本文所述方法所得到的恒功率因数的DG运行域,绿色区域表示仿真逼近法所得到的近似精确解运行域,紫色区域完全在绿色区域之内,说明了本文所提方法的准确性,而范围略有缩小则是由于忽略高阶波动量以及线性近似法所造成的。由图4还可看出,只要保证节点27的C相的波动在300～462 kW范围以内时,节点47的A相在最大波动范围内任意波动可满足各节点电压在安全阈值范围以内,且馈线容量和反向潮流也均满足要求。

本文方法也可用于求解DG、负荷同时变化时的运行域。当节点27的C相处接入负荷波动最大范围为-400～-200 kW时,节点47的A相处接入出力波动范围为300～500 kW的DG,此时运行域见附录E图E1,DG、负荷在其最大范围内任意波动均可满足配电网安全运行要求。而若该DG与该负荷位置对调,运行域求解结果为无解,则表明该网络状态下需要通过改变注入有功和无功功率、改变DG接入位置等其他技术手段来保证系统的运行安全。由此可见,DG、负荷的运行域会随着接入位置、波动范围的改变而改变,运行域的求解结果可以为DG的选址提供参考依据。

3.5 PQ型DG运行域

在27节点的C相处安装PQ型DG,即该DG的有功功率最大波动为200～400 kW,最大视在功率为600 kvar。计算得到PQ型DG在此波动情况下的各节点电压情况见附录F图F1。

A相和C相中均存在电压越限的问题,因此需要计算可满足各节点电压、线路安全的DG二维运行域,如图5所示。图中:Q27为节点27的负荷无功功率。

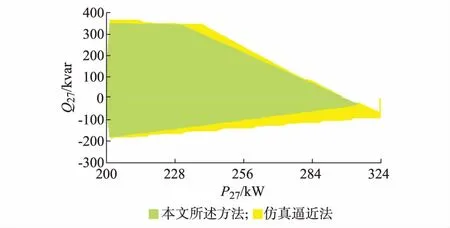
图5 二维PQ型DG运行域Fig.5 Two-dimensional dispatchable region of DG with PQ type

图5中,整个运行域在DG最大视在功率的扇形区域内,绿色区域为本文所述方法求解得到的PQ型DG运行域,黄色区域为用仿真逼近法求解得到的近似精确解,黄色区域完全覆盖绿色区域,超出边界的误差也较小,故该算法是有效的。

由于三相不平衡配电网各相间的耦合作用,同一波动范围的DG安置在同一节点的不同相也会对配电网的潮流产生不同影响。附录F图F2是将同一DG接入同一节点(节点27)的A相、B相时,用本文所提算法求解出的DG运行域结果。

对比图5和附录F图F2可知,同一DG接入节点27三相的运行域形态各有不同。若DG通过节点27的A相、B相并网,在无功可调的情况下,该网络最多可接纳的DG的有功输出为400 kW(见附录F图F2)。而若DG通过节点27的C相并网,其允许的最大有功输出为314 kW(如图5所示), 此时系统的安全运行状态集合为一临界点,难以承受系统的扰动。因此从系统尽可能多地接纳DG输出的角度出发,通过观察DG运行域可以发现DG接入A相、B相更为合适。

3.6 运算时间比较

不同场景下,本文所提算法和传统仿真逼近法(取样规模为103次)的计算时间见附录G表G1。

在不同的算例中,本文所提算法效率较仿真逼近法相差100倍左右,计算效率远高于仿真逼近法。在取样规模相同的情况下,仿真逼近法运行时间变化不大,而本文算法在计算过程中一旦出现越界情况就不再求解线性模型的最优值,故运行域越小，时间越短。

4 结语

不确定性DG接入配电网后,易导致电压频繁波动、过电压与欠电压等问题。本文基于仿射算术提出了一种可适用于三相不平衡配电网的不确定性DG运行域求解方法,通过基于仿射算术的近似线性潮流得到电压关于DG不确定量的线性关系,将其代入以电压安全约束、馈线容量约束和反向潮流约束为约束条件的DG运行域优化模型中,求得多个DG或负荷的完整运行域边界。

本文所提算法属于优化算法,可用于优化模型中作为约束条件,后续可将本文所提DG运行域的求解方法扩展应用于三相不平衡配电网的其他优化运行、控制问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参 考 文 献

[1] 王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.

WANG Chengshan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[2] MOKHTARI G, NOURBAKHSH G, ZARE F, et al. Overvoltage prevention in LV smart grid using customer resources coordination[J]. Energy and Buildings, 2013, 61: 387-395.

[3] 许晓艳,黄越辉,刘纯,等.分布式光伏发电对配电网电压的影响及电压越限的解决方案[J].电网技术,2010,34(10):140-146.

XU Xiaoyan, HUANG Yuehui, LIU Chun, et al. Influence of distributed photovoltaic generation on voltage in distribution network and solution of voltage beyond limits[J]. Power System Technology, 2010, 34(10): 140-146.

[4] 胡骅,吴汕,夏翔,等.考虑电压调整约束的多个分布式电源准入功率计算[J].中国电机工程学报,2006,26(19):13-17.

HU Hua, WU Shan, XIA Xiang, et al. Computing the maximum penetration level of multiple distributed generators in distribution network taking into account voltage regulation constraints[J]. Proceedings of the CSEE, 2006, 26(19): 13-17.

[5] IEEE standard for interconnecting distributed resources with electric power systems: IEEE Std 1547—2003[S]. New York, USA: The Institute of Electrical and Electronics Engineers, 2009.

[6] 刘科研,刘永梅,盛万兴,等.考虑电压约束的分布式电源接入配电网最大准入容量计算方法[J].电力自动化设备,2016,36(6):81-87.

LIU Keyan, LIU Yongmei, SHENG Wanxing, et al. Maximal allowable DG penetration capacity calculation considering voltage constraints[J]. Electric Power Automation Equipment, 2016, 36(6): 81-87.

[7] 余贻鑫,李鹏,贾宏杰.基于混合法的潮流可行域边界计算[J].电力系统自动化,2004,18(13):18-25.

YU Yixin, LI Peng, JIA Hongjie. Computing the boundary of the power flow feasible region based on the hybrid method[J]. Automation of Electric Power Systems, 2004, 18(13): 18-25.

[8] 余贻鑫,李鹏,孙强,等.电力系统潮流可行域边界拓扑性质及边界算法[J].电力系统自动化,2006,30(10):6-11.

YU Yixin, LI Peng, SUN Qiang, et al. Study on topological properties of boundary of power flow feasibility region and algorithm for boundary computation[J]. Automation of Electric Power Systems, 2006, 30(10): 6-11.

[9] 肖峻,张苗苗,祖国强,等.配电系统安全域的体积[J].中国电机工程学报,2017,37(8):2222-2230.

XIAO Jun, ZHANG Miaomiao, ZU Guoqiang, et al. Volume of distribution system security region[J]. Proceedings of the CSEE, 2017, 37(8): 2222-2230.

[10] 刘佳,程浩忠,李思韬,等.考虑N-1安全约束的分布式电源出力控制可视化方法[J].电力系统自动化,2016,40(11):24-30.DOI:10.7500/AEPS20150512002.

LIU Jia, CHENG Haozhong, LI Sitao, et al. Visualization method of output power control of distributed generators consideringN-1 security constraint[J]. Automation of Electric Power Systems, 2016, 40(11): 24-30. DOI: 10.7500/AEPS20150512002.

[11] 肖峻,祖国强,周欢,等.有源配电网的全象限安全域[J].电力系统自动化,2017,41(21):79-85.DOI:10.7500/AEPS20170119001.

XIAO Jun, ZU Guoqiang, ZHOU Huan, et al. Total-quadrant security region for active distribution network[J]. Automation of Electric Power Systems, 2017, 41(21): 79-85. DOI: 10.7500/AEPS20170119001.

[12] 王博,肖峻,周济,等.主动配电网中分布式电源和微网的运行域[J].电网技术,2017,41(2):364-370.

WANG Bo, XIAO Jun, ZHOU Ji, et al. Dispatchable region of distributed generators and microgrids in distribution systems[J]. Power System Technology, 2017, 41(2): 364-370.

[13] PICCOLO A, VACCARO A, VILLACCI D. Thermal rating assessment of overhead lines by affine arithmetic[J]. Electric Power Systems Research, 2004, 71: 275-283.

[14] 丁涛,柏瑞,郭庆来,等.一种非迭代仿射算法的输电网区间潮流计算方法[J].中国电机工程学报,2013,33(19):76-83.

DING Tao, BO Rui, GUO Qinglai, et al. A non-iterative affine arithmetic methodology for interval power flow analysis of transmission network[J]. Proceedings of the CSEE, 2013, 33(19): 76-83.

[15] GARCES A. A linear three-phase load flow for power distribution systems[J]. IEEE Transactions on Power Systems, 2016, 31(1): 827-828.

[16] GARCIA P A N, PEREIRA J L R, CARNEIRO J S, et al. Three-phase power flow calculations using the current injection method[J]. IEEE Transactions on Power Systems, 2000, 15(2): 508-514.

[17] 王洋.主动配电网优化运行策略研究[D].南京:东南大学,2016.

[18] GU W, LUO L, DING T, et al. An affine arithmetic-based algorithm for radial distribution system power flow with uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2014, 58: 242-245.