考虑需求响应的负荷控制对供电可靠性影响分析

雷 敏, 魏务卿, 曾进辉, 莫霜叶

(湖南工业大学电气与信息工程学院, 湖南省株洲市 412007)

0 引言

需求响应作为一种调节用户负荷的手段,其利用电价或激励机制,通过削峰填谷达到降低峰负荷时段电网潜在风险的目的,提高了系统可靠性。利用需求响应平滑负荷曲线来提高电力系统运行的安全性与可靠性是未来智能电网发展的重要手段之一,其中分时电价作为最为常见的电价模式与激励模式已被广泛采用[1-3]。然而,对于评估需求响应对电网供电可靠性的影响,目前主要局限于单一措施下的需求响应,因此本文给出包含负荷控制激励的分时电价下电网供电可靠性分析与计算方法。

欧洲各国政府将需求响应作为改善用户用电习惯的一种重要工具已推广应用多年,让消费者充分地参与到调节负荷过程,并以减少或转移消费作为条件机制,起到降低风险、提高可靠性的作用[4-6]。中国同样对可中断负荷的负荷控制与以分时电价为代表的多种需求响应模式大力推广实施,并取得了一定的成效[7-10]。目前需求响应的相关理论正在不断完善,需求响应下配电网可靠性研究已有相关资料,但是多种需求响应措施下负荷变化对配电网可靠性影响的研究较少。文献[11-12]研究激励型需求响应在微网包含可再生能源条件下对配电网的影响,考虑负荷削减策略,研究需求响应下的可靠性指标变化。文献[13]构建分时电价在电力市场中的变分不等式模型,研究了分时电价在不同市场结构收益变化引起负荷改变对配电网的影响。文献[14]将需求响应与配电网拓扑结构相结合,研究需求响应在不同的配电网分布网络中的影响程度。文献[15]从负荷与可靠性指标角度对分时电价与配电网可靠性做了定性分析,将修正优化后的负荷用二分法计算加权后的可靠性指标；文献[16]则从负荷转移与节约用电角度说明需求响应策略对配电网可靠性的影响。上述文献是在需求响应单一模式下对配电网可靠性进行研究,并且大都是从定性角度进行分析。在某些情况下,实施需求响应过程中往往会在基于电价措施的基础上对部分负荷采取控制措施,对参与负荷控制的用户给予补偿,综合两者优点。当实施需求响应分时电价模式中引入负荷控制时会对负荷产生额外的影响,对比分时电价单一模式下负荷曲线并不相同。因此,研究在分时电价下负荷控制对供电可靠性的影响很有必要。

本文提出一种新的适用于需求响应条件下的配电网可靠性计算方法,考虑同时采用两种需求响应措施对负荷的作用,利用年负荷曲线计算电网动态下的可靠性指标。首先,推导出在用户最大利益下分时电价包含负荷控制激励的负荷模型,引入遗传算法对需求响应负荷进行优化,得出优化后的分时电价与激励值,并将其代入需求响应负荷模型,得到优化后的需求响应负荷。根据改进的k均值聚类算法对负荷曲线聚类得到负荷概率模型,然后将聚类后的多个负荷值代入配电网,根据蒙特卡洛法进行模拟,得到可靠性指标,最后利用概率分布加权得出最终的配电网可靠性指标结果。

1 两种需求响应措施对负荷的影响

需求响应主要通过激励补偿措施与分时电价对用户形成合理的用电导向,而用户的响应过程能够从负荷曲线变化中直接反映。建立考虑负荷控制的分时电价负荷模型,是为得到两种不同机制下的需求响应负荷,更有利于分析实际应用多种需求响应措施环境中的系统可靠性。

1.1 分时电价的峰、谷时段划分

对负荷进行时段划分事关用户响应程度,影响分时电价削峰填谷效果。有效的划分结果能准确地描述出峰谷特性,反映负荷峰谷之间的内在联系。

模糊聚类具有优秀的处理模糊信息能力,该方法能够有效、合理地对一天24 h内负荷峰、谷、平时段进行划分。

首先引入峰隶属度Uup，t与谷隶属度Udown，t来衡量原负荷每小时负荷量的峰谷程度:

(1)

式中:b为原负荷一天中的负荷最大值；a为原负荷一天中的负荷最小值；qt为一天中每一小时的负荷值。

将一天中所得到的24组峰谷隶属度放入特征指标矩阵X中,即

X=[Uup，tUdown，t]24×2

(2)

随后,利用距离法中绝对值减数法构造模糊相似矩阵:

(3)

式中:Xik和Xjk分别为特征指标矩阵X中第i行、第k列和第j行、第k列的元素；c为0～1,使得所有Rij值的范围同样为0～1之间,当i=j时Rij=1。

然后,再通过平方法求得传递闭包,对上式求得的相似矩阵内数值不断取平方,即

R→R2→R4→…→R2n

(4)

当第一次出现Rk×Rk=Rk时,此时的Rk即为所求得的传递闭包。将传递闭包中出现过的值赋给λ,求取关于传递闭包的λ-截矩阵,不同取值会产生不同的分类结果。而最后所得出的划分结果为峰、谷、平三种情况,因此根据不同值聚类情况仅保留分类数为3的分组,然后依分组数得出分子自由度与分母自由度。以α=95%置信度计算F检验临界值作为标准值,同时计算保留下来λ-截矩阵的F统计量,计算公式为:

(5)

(6)

将保留的每一组计算后的F值与F临界表中标准值进行比对,去掉低于标准值数组分类情况。对于剩下的分组,F值越大，意味着类与类区别越显著,分类越合理,保留F值最高的一组分类情况作为最终峰、谷、平时段划分的结果。

1.2 负荷控制下的分时电价负荷模型

负荷控制下的分时电价负荷模型是用来描述在施行需求响应后,用户基于不同时间段电价变化与激励补偿后的负荷。用弹性系数表示对价格的需求敏感度。由前面得到的时段分组数据与不同时段定价,通过构建一天中24 h价格弹性矩阵与激励值,得出用户最大收益下的用电需求量值,以此作为响应后的负荷。弹性系数可表示为:

(7)

式中:q为用户用电需求值；ρ为目前电价；ρ0和q0分别为初始电价和未采用需求响应前的负荷量。

而对于某一时刻的弹性系数而言,一般又分为两类,假设:

(8)

式中:Δd(ti)为ti时刻的负荷改变量；Δρ(ti)和Δρ(tj)分别为ti和tj时刻的电价变化量；ξi,i为自弹性系数,表示i时刻电量改变与i时刻电价变化的关系；ξi,j为交叉弹性系数，一般大于等于零,表示i时刻电量改变与j时刻电价变化的关系。

在已知时段划分结果与各时段电价的情况下可以求得一天24×24 h价格弹性矩阵E,其表达式如式(9)所示。

(9)

对于需求响应负荷模型而言,一般分为单时段模型与多时段模型[17]。

1)单时段负荷模型表示负荷不能转移到一天中其他的时间段,通常此类负荷敏感度用自弹性系数表示,一般小于等于零。此时主要通过签订补偿激励合约对负荷进行控制,在切除负荷后给予一定的补偿。

对于单时段负荷控制下而言,用户用电收益S可表示为:

S(d(i))=Id(d(i))-d(i)p(i)+

(d0(i)-d(i))A(i)

(10)

式中:i=1,2,…,24；d0(i)为原负荷需求量；d(i)为需求响应优化后的负荷；Id(d(i))为用户在需求响应模式下时段i的收入；p(i)和A(i)分别为该时段电价和补偿激励值,负荷控制一般对峰负荷进行控制削减,故激励值A(i)只针对峰时段进行补偿,其余时段为零。

当∂S/∂d(i)=0时,用户获得利益最大化,此时收益达到最高点。文献[18]介绍了一种计算某一时段用户收入的普遍方法,通过电价与弹性系数关系计算用户在该时段的收入:

Id(d(i))=It(d(i))+

(11)

式中:下标0表示对应变量的初始值；It(d(i))为传统模式下时段i的收入；E(i,i)为E第i行、第j列元素。

结合式(11)可以得到单时段用户按最大收益下的负荷模型:

(12)

当激励值A(i)为零时,d(i)=d0(i),此时负荷并没有改变,E(i,i)所代表的自弹性系数为零,这表明对于不可转移的单时段负荷只能通过激励措施并采取负荷控制来减少峰时段用电负荷。

2)多时段负荷模型则表示负荷可以转移到其他的时间段,负荷敏感度一般不小于零,通过设置分时电价可引导用户将部分峰负荷转移到其他时段[19]。

首先假设dq/dρ为定值,并考虑额外的需求响应激励作用,对峰时段削减的负荷给予A(j)补偿,则用电需求与不同价格之间的对应关系可用下列线性表达式表示:

d(i)=d0(i)+

(13)

综合单时段负荷模型与多时段负荷模型得出分时电价及激励值与用电需求之间的关系,最终包含负荷控制激励的分时电价负荷模型如下:

d(i)=d0(i)+

i=1,2,…,24

(14)

在已知激励值与各时段电价后,按照式(14)可以得到在分时电价负荷控制基础上，用户按最大收益条件下一天中的负荷趋势,以此作为实施两种需求响应措施后的用户负荷模型。

2 需求响应下的可靠性计算

2.1 需求响应负荷优化模型

负荷是需求响应影响供电可靠性的关键因素,需求响应负荷对不同时段电价与激励值十分敏感。为较好地体现需求响应削峰填谷效果,对分时电价的制定与激励值进行优化,得到两种措施下的需求响应负荷优化模型。

为此,将优化目标设为峰负荷最小与峰谷差最小,决策变量由峰时电价ppeak、平时电价poff-peak、谷时电价plow与激励值A组成。约束条件包含发电成本边界约束、价格关系约束与发电总量不变约束。

通过式(14)可以得到目标函数,优化函数如下:

(15)

式中:d为由式(14)求得的一天中两种措施下需求响应负荷；d0为一天内的原负荷。

对于处理带约束的多目标问题可以采用遗传算法,结合每一日的原负荷值与两种措施下的负荷模型,将目标函数与约束条件代入即可得到分时电价与激励值的近似最优解。在得到优化后的分时电价与激励值之后,将其代入式(14)算出最终优化后的需求响应负荷值。

2.2 负荷聚类下的需求响应配电网可靠性计算方法

一般情况下的配电网可靠性评估是以系统中负荷的最大值为依据计算配电网在峰负荷下的可靠性指标大小,无法反映在动态负荷下可靠性的改变。采用传统方法分析需求响应下的系统可靠性指标,很难体现需求响应对负荷整体作用带给系统可靠性的变化。若直接将负荷曲线代入可靠性评估中,由于其负荷值众多,计算十分困难。因此,需要聚类方法将负荷曲线分为较少的类,并以此刻画不同模式下整体负荷曲线[20]。本文采用改进型k-means聚类算法,以年负荷曲线为对象对需求响应负荷曲线进行聚类,计算需求响应动态负荷下的可靠性指标,建立多级年负荷模型[21]。

先求得需求响应下的年负荷曲线,把原负荷中每一日的负荷值与时段划分结果代入需求响应负荷优化函数,得出每一日分时电价与激励值的优化结果,并将其代入两种措施下的需求响应负荷模型,得到不同措施下的需求响应年负荷曲线。

随后,利用改进的k-means聚类算法对需求响应负荷中每一天的最大负荷值进行聚类,得到聚类分组结果与分布概率。将每一组负荷代入配电网蒙特卡洛模拟过程[22],算出不同组可靠性指标,通过与分布概率的加权得出系统最终的可靠性指标值,具体流程如下。

步骤1:先通过1.1节所提的时段划分方法确定原负荷中每一天的峰、谷、平时间段。

步骤2:在峰、谷、平时段确定的情况下,利用式(15)对式(14)中需求响应负荷模型进行优化,得到优化后的峰、谷、平电价与激励值。

步骤3:根据每一天对应的时段、优化后的分时电价与激励值,将其代入式(14)即可得到两种措施下需求响应年负荷曲线。

步骤4:将需求响应年负荷曲线里每一日峰负荷代入改进型的k-means聚类算法,取一年中每日峰负荷的不同值个数为n,则聚类数k=1+lgn/lg 2。先利用层次聚类确定聚类中心,随后按照传统k-means聚类算法对其聚类,直至聚类结果不发生变化,从而得到聚类后负荷的分组与分布概率。

步骤5:把聚类后的每一组负荷代入配电网蒙特卡洛模拟法中,考虑联络线的负荷转移作用,得出系统在需求响应年负荷曲线下的可靠性指标,并将每一组计算得到的可靠性指标与分布概率加权,得出最终动态负荷下的需求响应可靠性指标。

3 仿真分析

3.1 算例说明

本文以修改的RBTS-BUS6为对象,在馈线F1与F2之间增加一条1 MW容量馈线,馈线F1与F2的容量为2 MW,其余不变。利用MATLAB平台编写包含改进型k-means负荷聚类算法的RBTS-BUS6配电网可靠性评估程序,并通过其中的遗传算法工具箱对两种模式下的需求响应负荷优化。先求出需求响应调整后的年负荷曲线,分析不同需求响应模式对负荷的影响。然后将负荷曲线进行聚类,并对聚类结果进行显著性分析以验证其准确性。最后,将聚类结果代入蒙特卡洛模拟过程计算配电网可靠性指标,对比不同需求响应措施下的系统可靠性指标变化。

3.2 需求响应下的负荷调整

先按照本文第1节内容方法对一年中配电网8 760个总原始负荷进行时段划分,在得到每一日的负荷时段划分后,通过需求响应负荷优化模型得到分时电价负荷控制下的年负荷曲线。抽取其中某一日数据为典型日,其时段划分为:峰时段10:00—12:00,19:00—21:00；平时段08:00—10:00,12:00—19:00,21:00—23:00；谷时段00:00—08:00,23:00—24:00。在此时间分段结果下,初始电价为0.7元/(kW·h),价格弹性系数、优化后的电价与激励值如表1所示,无负荷控制分时电价负荷、负荷控制下的分时电价负荷和原负荷三者关系如图1所示。

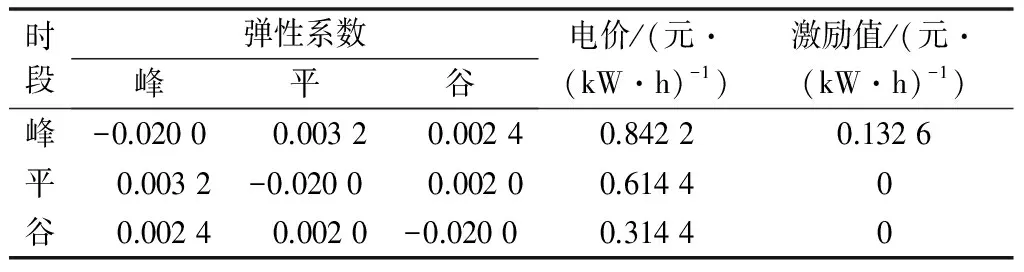
表1 分时电价弹性系数与激励值Table 1 Elasticity coefficient of time-of-use electricity price and incentive value

可以看到,在分时电价作用下,峰负荷下降、谷负荷上升,峰谷负荷差值减小。而加入负荷控制后可以将峰时段不可转移的负荷进一步降低,对于峰时段不可转移的负荷通过基于电价的需求响应措施无法改变,而通过负荷控制能够直接切除部分该负荷,在给予补偿的条件下对此类负荷进行控制,能够取得很好的效果。且就整体负荷而言,加入负荷控制后的负荷曲线更为平滑。

在不同的需求响应模式下,30 d最大负荷如图2所示。可以看到,包含负荷控制的需求响应措施日最大负荷最小,仅在分时电价作用下的负荷相比原负荷在峰时段得到了有效的降低。其中,当负荷水平较高时,两种需求响应模式降低峰负荷较为明显,而在低水平下时仅略有降低。这说明本文需求响应负荷的优化模型能够根据实际负荷水平,降低峰负荷,平缓负荷曲线。

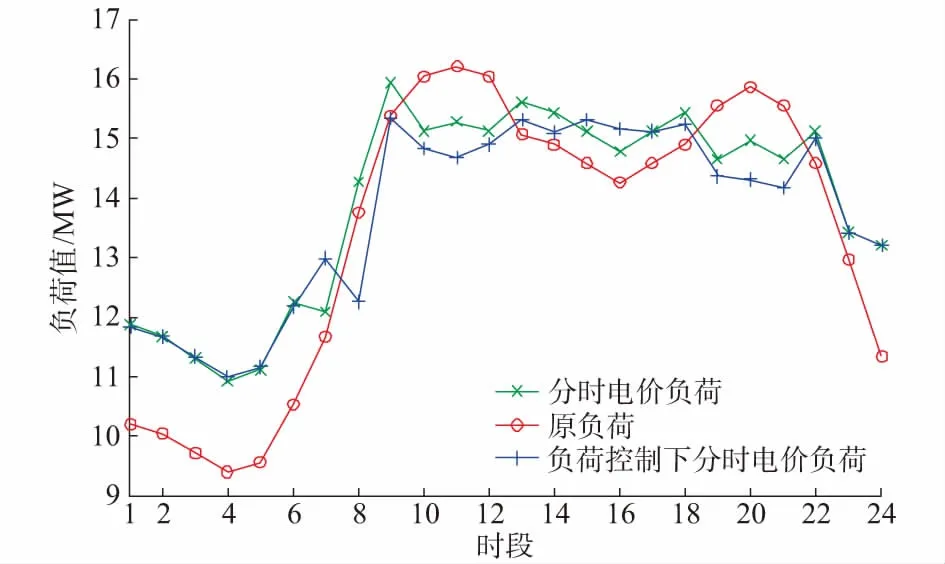
图1 不同需求响应模式下的日负荷曲线Fig.1 Daily load curves under different demand response modes

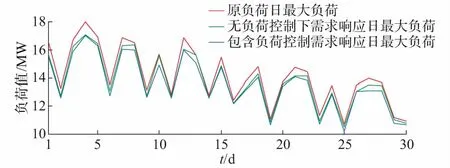
图2 需求响应30 d日负荷峰值变化Fig.2 Peak value changes of daily load for demand response in thirty days

3.3 负荷聚类结果显著性分析

将原负荷与不同模式下需求响应年负荷曲线中每日峰负荷提取出来,依照改进的k-means聚类算法对其进行聚类,得到3组不同的分组情况。为确保聚类结果的准确性,对3组聚类数据进行显著性检验,其结果如表2所示。

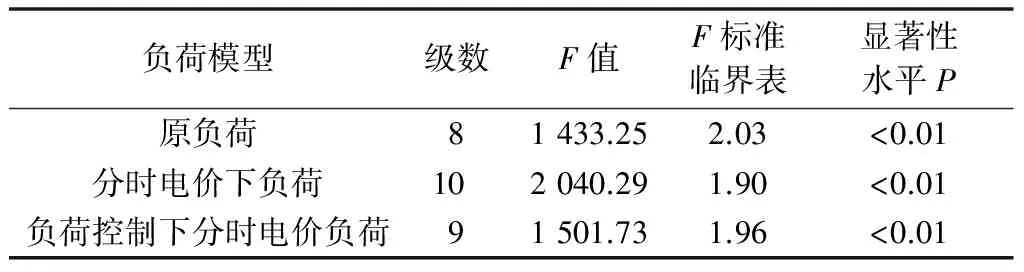
表2 不同需求响应下的负荷聚类显著性结果Table 2 Significant results of load clustering under different demand responses

可以看到,聚类后的3组分类结果F值远远大于其查表值,且P值小于1%,这表明显著性差异存在,验证了分组结果的有效性。同时可以看到,聚类级数远低于365组,因此在利用负荷曲线对系统可靠性评估的过程中,能够有效地降低计算时间。

3.4 基于负荷聚类的可靠性评估

本文设计了3种方案评估配电网在动态负荷条件下的可靠性,并将不同需求响应模式下的负荷与原负荷可靠性指标进行对比,验证不同措施下的需求响应对配电网可靠性的影响。

方案1是在不采取任何一种需求响应措施的情况下,将原负荷代入2.2节中负荷聚类下的配电网可靠性计算方法,对系统可靠性指标进行计算；方案2对只采取分时电价单一需求响应模式下的系统可靠性指标进行计算；方案3则是在考虑负荷控制激励与分时电价两种需求响应机制下对系统的可靠性指标进行计算。

由文献[23]可知配电网各项指标的计算方法,3种方案计算得到的可靠性指标如表3所示。

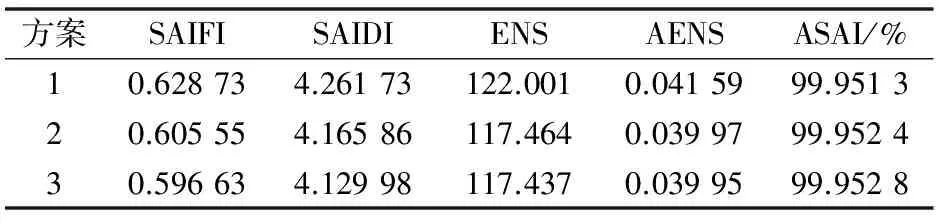
表3 可靠性指标计算结果Table 3 Calculation results of reliability indices

通过将方案1与另外两种方案对比可知,两种不同需求响应模式均能有效降低系统平均停电频率与平均停电时间,其中包含负荷控制的方案3的系统指标最优。从系统供电不足角度看,采用单一措施后的分时电价负荷能大幅度降低系统电量不足期望值(ENS)与平均电量不足期望值(AENS),而包含负荷控制的分时电价相比略有降低。

总体而言,系统在包含负荷控制的分时电价环境下可靠性最高,单一分时电价次之,且采取需求响应后的系统可靠性远高于不采取需求响应的系统。由于分时电价能够转移部分峰时段负荷到其他时段,从而降低系统峰负荷,而在加入负荷控制后,能够直接削减部分峰负荷,若峰时段发生故障则较低的负荷通过联络线与其他馈线相连能够保障更多的负荷点供电,因此减少了部分负荷点的停电总次数与总时间,系统平均停电次数(SAIFI)、系统平均断电持续时间(SAIDI)及ENS指标得到了降低,系统平均停电频率(ASAI)指标最高。

4 结论

本文引入分时电价与负荷控制激励两种需求响应机制,得出不同的需求响应模式负荷,通过对配电网负荷曲线聚类,得到评估配电网在需求响应动态负荷下的可靠性。利用改进型k-means聚类算法对年负荷曲线进行快速聚类,结合配电网蒙特卡洛模拟法,在考虑联络线负荷转移的条件下建立配电网负荷曲线聚类可靠性评估算法,计算其可靠性指标,对比仿真结果可以得出如下结论。

1)需求响应能够提高系统的可靠性,相比单一的需求响应措施,在分时电价的基础上考虑负荷激励措施能够获得更高的系统可靠性。

2)负荷控制能够削减部分峰时段的不可转移负荷,在结合分时电价后,能在单一的分时电价转移部分峰时段负荷到其他时段的基础上,进一步降低峰负荷,在联络线容量一定的情况下保证更多的负荷点不受故障影响。因此,在某些要求高可靠性的供电环境中,可以采用负荷控制激励与分时电价两种措施下的需求响应保障系统的可靠供电。

本文建立了两种需求响应机制下的负荷模型,分析不同需求响应措施在联络线负荷转移条件下对配电网可靠性的影响。但对于配电网应用场景而言,未考虑负荷控制对分布式能源作用从而引起的系统可靠性变化,在后续的研究中将对智能配电网场景进行丰富,结合微网能量管理系统,分析不同需求响应模式对配电网供电可靠性的影响。

参 考 文 献

[1] 张钦,王锡凡,王建学,等.电力市场下需求响应研究综述[J].电力系统自动化,2008,32(3):97-106.

ZHANG Qin, WANG Xifan, WANG Jianxue, et al. Survey of demand response research in deregulated electricity markets[J]. Automation of Electric Power Systems, 2008, 32(3): 97-107.

[2] EVANGELOPOULOS V A, GEORGILAKIS P S, HATZIARGYRIOU N D. Optimal operation of smart distribution networks: a review of models, methods and future research[J]. Electric Power Systems Research, 2016, 140: 95-106.

[3] PATERAKIS N G, ERDINÇ O, CATALO J P S. An overview of demand response: key-elements and international experience[J]. Renewable & Sustainable Energy Reviews, 2017, 69: 871-891.

[4] LAMPRINOS I, HATZIARGYRIOU N D, KOKOS I, et al. Making demand response a reality in Europe: policy, regulations, and deployment status[J]. IEEE Communications Magazine, 2016, 54(12): 108-113.

[5] AALAMI H, YOUSEFI G R, MOGHADAM M P. Demand response model considering EDRP and TOU programs[C]// Transmission and Distribution Conference and Exposition, April 21-24, 2008, Chicago, USA: 1-6.

[6] 谢珍建,于乐,归三荣,等.国外需求响应技术在主动配电网中的应用[J].电力需求侧管理,2015,17(2):59-60.

XIE Zhenjian, YU Le, GUI Sanrong, et al. Application of foreign demand response technology in active distribution network[J]. Power Demand Side Management, 2015, 17(2): 59-60.

[7] 田世明,王蓓蓓,张晶.智能电网条件下的需求响应关键技术[J].中国电机工程学报,2014,34(22):3576-3589.

TIAN Shiming, WANG Beibei, ZHANG Jing. Key technologies for demand response in smart grid[J]. Proceedings of the CSEE, 2014, 34(22): 3576-3589.

[8] 高赐威,陈曦寒,陈江华,等.我国电力需求响应的措施与应用方法[J].电力需求侧管理,2013,15(1):1-4.

GAO Ciwei, CHEN Xihan, CHEN Jianghua, et al. Measures and application of China’s demand response[J]. Power Demand Side Management, 2013, 15(1): 1-4.

[9] 王蓓蓓.面向智能电网的用户需求响应特性和能力研究综述[J].中国电机工程学报,2014,34(22):3654-3663.

WANG Beibei. Research on consumers’ response characterics and ability under smart grid: a literatures survey[J]. Proceedings of the CSEE, 2014, 34(22): 3654-3663.

[10] 许子智,曾鸣.美国电力市场发展分析及对我国电力市场建设的启示[J].电网技术,2011,35(6):161-166.

XU Zizhi, ZENG Ming. Analysis on electricity market development in US and its inspiration to electricity market construction in China[J]. Power System Technology, 2011, 35(6): 161-166.

[11] AGHAJANI G R, SHAYANFAR H A, SHAYEGHI H. Demand side management in a smart micro-grid in the presence of renewable generation and demand response[J]. Energy, 2017, 126: 622-637.

[12] 周保荣,黄廷城,张勇军.计及激励型需求响应的微电网可靠性分析[J].电力系统自动化,2017,41(13):70-78.DOI:10.7500/AEPS20160926016.

ZHOU Baorong, HUANG Tingcheng, ZHANG Yongjun. Reliability analysis on microgrid considering incentive demand response[J]. Automation of Electric Power Systems, 2017, 41(13): 70-78. DOI: 10.7500/AEPS20160926016.

[13] CELEBI E, FULLER J D. Time-of-use pricing in electricity markets under different market structures[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1170-1181.

[14] MEDINA J, MULLER N, ROYTELMAN I. Demand response and distribution grid operations: opportunities and challenges[J]. IEEE Transactions on Smart Grid, 2010, 1(2): 193-198.

[15] 赵洪山,王莹莹,陈松.需求响应对配电网供电可靠性的影响[J].电力系统自动化,2015,39(17):49-55.DOI:10.7500/AEPS20150205007.

ZHAO Hongshan, WANG Yingying, CHEN Song. Impact of demand response on distribution system reliability[J]. Automation of Electric Power Systems, 2015, 39(17): 49-55. DOI: 10.7500/AEPS20150205007.

[16] KAHROBAEE S, ASGARPOOR S. The effect of demand side management on reliability of automated distribution systems[C]// IEEE Technologies for Sustainability, August 1-2, 2013, Portland, USA: 179-183.

[17] AALAMI H A, MOGHADDAM M P, YOUSEFI G R. Demand response modeling considering interruptible/curtailable loads and capacity market programs[J]. Applied Energy, 2010, 87(1): 243-250.

[18] SCHWEPPE F C, CARAMANIS M C, TABORS R D, et al. Spot pricing of electricity[M]. USA: Springer, 1988.

[19] AZAMI R, FARD A F. Impact of demand response programs on system and nodal reliability of a deregulated power system[C]// IEEE International Conference on Sustainable Energy Technologies, November 24-27, 2008, Singapore: 1262-1266.

[20] 邵黎.计及负荷变化的配电网可靠性评估模型与算法研究[D].重庆:重庆大学,2007.

[21] 陈凡,刘海涛,黄正,等.基于改进k-均值聚类的负荷概率模型[J].电力系统保护与控制,2013,41(22):128-133.

CHEN Fan, LIU Haitao, HUANG Zheng, et al. Probabilistic load model based on improvedk-means clustering algorithm[J]. Power System Protection and Control, 2013, 41(22): 128-133.

[22] ZHAO H S, LIU H Y, CHEN S, et al. Reliability assessment of distribution network considering preventive maintenance[C]// IEEE Power and Energy Society General Meeting, July 17-21, 2016, Boston, USA: 1-5.

[23] IEEE guide for electric power distribution reliability indices-redline[S]. 2012.