关于能源转型分析的评述(二)不确定性及其应对

舒印彪, 薛禹胜, 蔡 斌, 凌 文, 韩建国, 陈新宇, M. B. MCELROY

(1. 国家电网有限公司, 北京市100031; 2. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106;3. 智能电网保护和运行控制国家重点实验室, 江苏省南京市 211106; 4. 国家能源投资集团有限责任公司, 北京市 100011;5. 哈佛大学工程与应用科学学院, 剑桥 MA 02138, 美国)

0 引言

一个普遍的共识是:唯一确定的是不确定性(the only certainty is uncertainty)。长期以来,关于不确定性的讨论已成为科学与工程技术领域最重要的问题之一[1-4]。

能源转型不仅涉及与能源技术、气候等相关的自然科学,还涉及与能源经济、政策机制、人的行为等相关的社会科学,是一个典型的需要在信息—物理—社会环境框架下考虑的能源(cyber-physical-social system in energy,CPSSE)问题[5-6]。

能源政策或能源企业战略的制定依赖于能源转型的分析结论。但由于信息及认知的不足,能源转型问题的相关决策者或研究者需面对大量的来自物理、经济、政策、行为等领域的不确定性因素。

仿真是能源转型分析的基本研究方法,在问题提炼、模型构建、参数设置、仿真实验、结果分析等各个研究阶段均可能引入不确定性因素,并最终累积为结论的不确定性。

在不确定性情况下,研究人员或利益相关者感兴趣的重要问题主要包括但不限于:①不确定性因素将如何影响给定的能源转型方案的各项评估指标?②哪些因素的影响较大而不可忽视?③在不同的可能性场景下,能源如何转型?④何种能源转型目标与路径是风险最优的?⑤给定的某能源转型方案在极端不确定性条件下的强壮性如何?⑥应该如何施加干预措施来应对这些不确定性以最大化收益或降低风险?

若无法有效地应对不确定性因素以解答上述问题,则不仅会降低研究结论的科学性,更严重的后果是对实际的能源转型带来重大的潜在风险,导致转型的失败[7]。

目前,几乎所有的能源转型研究均已涉及对不确定性因素的分析,文献大多按引入环节将其分为参数与模型的不确定性[8-9]。主流的分析方法集中关注参数不确定性,包括:基于确定性模型的灵敏度分析[10]和多场景分析[11],以及随机规划[12]、模糊规划[13]、区间规划[14]等不确定性优化模型。应对模型不确定性的方法仍较少,包括:多准优解法[9]和多模型比较法[15]。

文献[16-18]归纳了在水资源管理、环境与生态、能源等领域的不确定性分析中所采用的分析方法,分析了各种方法的优缺点及其可应对的不确定性因素。

然而,实际应用中要求不确定性分析方法能够保证在有限的计算量下得到可信的结论,当前的研究并未很好地应对上述挑战,主要不足包括:①仅能分析单个或少数几个同时存在的不确定性因素,分析大量不确定性因素时面临组合爆炸;②简化处理已经意识到的描述不确定性因素时的困难,而把重点放在后续的影响分析环节[19];③外部扰动、利益相关者的行为等重要的不确定性因素被归为参数的不确定性,而未区分其与背景型参数之间的差异,不利于开展针对性的分析以揭示其影响;④可完成不同分析任务的各类方法之间缺乏有效的融合(如灵敏度分析得到的信息未用于指导随机规划研究中的场景构建),而结合多种方法来处理同时面临的各类不同特点不确定性因素的研究则更为鲜见。

本文将讨论能源转型分析中各类不确定性因素的不同特点;回顾各类已有的能源转型不确定性分析方法;针对存在大量不同特点不确定性因素所带来的实际困难,提出融合多种方法以兼顾计算量与准确性的综合分析框架。

1 不确定性因素的三个维度

1.1 不确定性的主客观本质

1.1.1不完善的知识

不同于微观粒子本质上的随机性,宏观尺度的世界被认为是确定与可知的。不确定性的本质是由于人们对关心的问题仅具备有限的知识(limited knowledge),即由认知的不足导致了不确定性。即便是混沌系统也是由于初始条件的微小变化很难准确刻画,但本质上仍是确定性的系统[20-22]。

有限的知识可能是因为该问题尚未得到很好的解答,也可能是已经有了可靠的结论但特定的研究人员、团体或机构并不掌握该知识。

1.1.2主客观本质的分类

不确定性的主客观本质并没有形成统一的分类方法。

诸多文献将不确定性分为随机不确定性(aleatory uncertainty)与认知不确定性(epistemic uncertainty)[23-25]。其中,随机性是指无法通过进一步的研究和实证工作而得到消除(至少在短期内)的认知不确定性。一个典型的例子是假设一枚掷向空中的均匀硬币落地后出现正反面的情况是随机的,概率各为50%。另一方面,则可以建立其结构和空气动力学模型来预测掷向空中的硬币的落地情况,但由于对机理不够了解或只有少量的数据,故在研究中假设其是随机过程适用于对其进行方便有效的建模与分析[26]。然而,此种分类方法中仍然使用认知不确定性来命名除随机性之外的不确定性,容易引起混淆。

文献[27]将不确定性分为随机性(random-ness)与模糊性(vagueness)。文献[28]将不确定性分为随机性、模糊性、不完全性、不稳定性与不一致性,并强调随机性与模糊性是最基本的。文献[29]将不确定性分为随机性、模糊性与粗糙性。

此外,由于包括科学词汇在内的自然语言具有多义性、含混性、依赖上下文、语义随时间发生变化等特性,部分文献提出应将语言不确定性视作有别于认知范畴的另一种不确定性[30-32]。其中,语义随时间发生变化的一个例子是“energy transition”在20世纪早期主要出现在量子电动力学(quantum electrodynamics)领域的研究中,而近年来则主要被用于表示能源系统结构的长期转型[33]。

限于篇幅,本文不对此问题展开,仅就随机性与模糊性进行介绍。

1.1.3随机性

随机性指结果与给定的场景之间没有必然的对应关系,或给定的场景的特征并不完整。随机不确定性也常被称为不可消除不确定性、客观不确定性或外部不确定性等。

随机不确定性的主要研究工具是概率论(probability theory)[34],当前的能源转型研究中采用过的概率分布包括正态分布、均匀分布、贝塔分布、三角分布等[35-36]。

1.1.4模糊性

模糊性是指由于事物本身概念不清楚或衡量事物的尺度不清楚,而造成分类的不确定性。模糊性是因为“概念”所引起的,是典型的由认知不足导致的不确定性。模糊性也常被称为可消除不确定性、主观不确定性或内部不确定性等。

模糊性的主要研究工具包括模糊集理论(fuzzy set theory)[37]、粗糙集理论(rough set theory)[38]、可能性理论(possibility theory)[39]、证据理论(evidence theory)[40]、信息间隙决策理论(information gap decision theory)[41]、区间分析(interval analysis)[42]等。

研究对象中的随机和模糊性往往同时存在,并放大各自的影响。近年来出现了一些同时处理两类不确定性的研究,其中,有些文献将概率论与其他工具相结合[43],有些则尝试通过单一的工具(如模糊集理论)来同时反映两种不确定性因素[44]。

可获取的知识和信息是研究者决定如何应对不确定性因素的重要依据。但在具体问题中还需根据研究目标、建模难度等方面进行综合权衡,因此,同一个不确定性因素在不同的研究中可能按随机或模糊进行处理[45]。

1.2 不确定性的来源

1.2.1模型与参数

1)模型

模型的不确定性可分为边界和结构的不确定性。

模型边界的不确定性是指在界定所研究对象系统的边界、设计概念和框架模型时面临的不确定性,包括外部的经济、政治、社会、技术环境等。能源转型问题极为复杂,为了保证研究的可操作性,不可能为所有涉及的环节均建立模型,必须确认其边界。若边界不准确,会影响后续所有环节的研究。

模型结构的不确定性源于对系统的理解不够充分,未能采用适当的数学方程描述输入量与变量、变量与变量、变量与输出量之间的函数关系,无法准确地反映实际系统间各要素之间的关系以及系统的整体动态特性。模型构建、校准、校核、验证等环节均可能引入不确定性。

显然,不同的研究人员对同一个实际问题可能抱有不同的看法,从而使用不同的模型。

2)参数

参数可分为模型参数和输入参数。前者用于描述能源系统模型本身的结构特性;后者是模型的输入量,确定了研究所针对的具体工况(见1.2.2节)。研究中涉及的参数种类以及参数所属的环节依赖于模型的边界及结构,同一个参数在一个模型中是输入参数,在另一个模型中可能是模型参数。

数据的采集测量、存储、分析、处理、表示等环节均可引入不确定性,不仅包括历史和现状的数据,还涉及对未来数据的预测或外推。由于关键性参数的不确定性对模型输出结果及决策制定具有显著的影响,需对这部分不确定性参数加以识别及分析。

参数的设置方法包括:①通用常数,如自然常数、光速;②固定参数,如标煤的热值、排放率等;③先验参数,对于较难通过模型校准来识别的参数,将其设定为一个固定的不变量,如能源转型过程中未来的贴现率、技术进步率,这些参数往往属于输入参数;④校准参数,没有明确的先期研究作为参数设置依据,需要通过比较模型的输入/输出结果与历史统计数据来校准,这些参数往往属于模型参数。其中,仅类型③和④存在不确定性。

1.2.2工况

能源转型研究中确定工况的输入参数均是表示相关变量未来几十年动态过程的时间轨迹,包括能源消费量、能源价格、碳排放价格、常规的技术进步率、新能源成本下降速度等;其不确定性可通过给定多条可能的时间轨迹及对应的概率来表示。

统计数据、实证研究数据、专家启发法等是常用的设置依据[19,46]。但很多情况下研究者不具备高质量信息作为描述参数不确定性的依据;即便那些有着充足历史数据的参数(如石油价格),其统计规律也并不一定适用于未来场景。专家启发法是缺乏统计和实证研究数据时可采用的高质量的主观性方法,但即便是专家亦不可避免地受到直觉推断、认知偏见、过度自信等因素的影响[47]。

但若无法合理确定参数及其不确定性的取值范围及概率分布,将导致后续环节的分析结果并不具备对实际问题的指导意义。

多个参数间可能存在因果关系尚未明确的相关关系,从而互相加剧或抵消单个不确定性对结果的影响,若要考虑上述影响,则需开展多参数不确定性分析,问题将十分复杂。

1.2.3扰动(或故障)

扰动(或故障)包括核泄漏事件、政策剧变、非预期性的能源技术突破、能源价格大幅波动等。扰动的发生有时会极大地影响能源转型的走势。水力压裂技术带来的页岩气革命、福岛核泄漏引起的部分国家的去核化等事件便是生动的例子。

在仿真研究中,每个扰动事件的描述可能需要包括:开始时刻、持续时间、幅度、发生地点、发生概率等。一次仿真中可设置多个扰动。扰动的设置依据与工况不确定性类似,但在信息质量上往往更差,更加依赖于专家启发法。

扰动可在仿真开始前便设置完毕;在有真实人参与的实验经济学仿真中,还可在动态的交互仿真过程中人为施加扰动。

1.2.4观点

观点的不确定性是指针对同一个问题,可能存在不同的观点。观点也属于认知的范畴,但观点的不确定性与认知的不确定性间的差异在于:认知的不确定性是指对于某个问题缺乏足够的了解,属于不确定性本质的讨论范畴;而观点的不确定性则是对于同一个问题抱有不同的认知或看法,属于不确定性来源的讨论范畴。

观点的不确定性可以是知识本身的不确定性,即针对该问题暂未形成主流的共识,同时存在多个不同的研究结论,该种情况在各个学科领域都普遍存在。以评估能源技术对健康和环境的负面影响为例,文献[48]比较了63份针对该问题的经过同行评议的研究结果,单份研究均以很小的不确定性范围给出了各类能源技术之间的相对顺序,但各份研究中的排序并不一致,若综合这些研究中各类能源技术的不确定性范围,则能够支持任何一种各类能源技术间的可能排序,即任何一种能源都可以被认为是负面影响最小的技术。

观点的不确定性也可以是对同一个可靠的知识抱有不同的认知。原因可能包括:知识的表达与传播方式不易理解、受众(政府、工业界、组织机构或民众等)的理解能力与原有立场存在差异等。例如,在气候变化研究领域最具权威性的政府间气候变化专门委员会(IPCC)在其2013年发布的第五次评估报告中指出,有95%以上的把握认为人类活动是近50年全球气候变化的主要原因[49],但奥巴马和特朗普两届美国政府对于气候变化及相关的政策持有截然相反的观点。

不同的观点将经由不同的行为影响能源转型。

1.2.5行为

如果人是完全理性的,则其行为的态度和偏好将是可预测的,从而不存在不确定性。但大量的观察与实验结论均表明,实际生活中人的决策行为系统性地偏离新古典经济学中基于“理性人”假设做出的描述与预测,表现出“有限理性”的特点[50-52]。

政策制定者、能源供应者、能源消费者等参与者的行为是能源转型的重要驱动因素,行为的不确定性是能源转型问题中不确定性的重要来源。因此,除了常规分析中所关注的因果型数据和无明确因果关系的统计型数据之外,能源转型问题还需重点分析大量人的行为数据,提炼相关的深层知识[53]。

行为的不确定性可表现为两个方面:不同参与者的行为偏好存在差异;同一个参与者的行为偏好无法保持一致性,两次面对同一个问题时可能做出不同的决策。

让真实人参与仿真或为其行为建立代理模型是能源转型研究中两类最主要的研究方法。一方面,参与者的决策量将以参数或扰动的形式参与到仿真计算中,其不确定性会体现为仿真中参数或扰动的不确定性;另一方面,由于人的行为难以用数学模型准确描述,所以行为的不确定性还会体现为模型的不确定性。

不同于其他在仿真开始前便事先设置完毕的参数或扰动,行为的不确定性体现在交互博弈仿真的过程之中。

此外,人的行为必然受到其对某个问题所持观点的影响,但观点所代表的是参与者对某问题的认知,行为则是将该认知付诸于具体的行动,在此过程中可能由于消极的情绪、认知的失调、受威胁的自尊、自律的失败、排斥与归属、决策疲劳等原因而不能真实反映其所持的观点[54]。

1.3 不确定性的认知程度

目前,文献中针对不确定性认知程度的讨论集中在随机性方面。文献[23]把对于随机性的认知程度分为:确定性(determinism)、统计型不确定性(statistical uncertainty)、场景型不确定性(scenario uncertainty)、意识到的无知(recognized ignorance)以及一无所知(total ignorance)。其中,统计型不确定性指可给出概率分布的不确定性,其命名源于该类不确定性可用统计学术语进行描述;场景型不确定性指仅可给出不确定性的范围,其命名源于该类不确定性常被刻画成多个场景并逐个进行研究。但上述命名方法无法明确地表示认知的深浅程度。

本文对不确定性认知程度的划分参见表1。

表1 不确定性认知程度的划分Table 1 Classification of uncertainties based on cognitive level

确定性因素不存在不确定性,故只需开展确定性条件下的分析;一无所知的因素则由于不掌握任何信息而无法开展分析。因此,不确定性分析中重点关注可给出概率分布或区间的随机性、可定性(量)区分的模糊性以及意识到的无知(下称“无知”)。

由于只掌握很少一部分可供研究的信息(如历史上仅有极少量的样本及案例),针对无知的研究以假定场景下的确定性分析为主,对实际问题描述的准确性可能不高。例如,研究由地震引起的核泄漏事故的影响至少需要解决如下子问题:该事故发生的可能性与强度,政府、企业、民众等在事故后对能源技术的看法及其随时间的变化情况,上述看法如何影响针对核电的政策,核电政策的变化如何影响能源企业的战略等。历史经验表明这些因素对于能源转型的发展趋势往往有着惊人的影响能力。因此,尽可能多地探索可能的不确定性空间是分析中需坚持的重要原则之一。

对于仅可给出区间的随机性,有些文献通过合理假设给出其概率分布。文献[12,57]根据拉普拉斯准则(Laplace criterion),在数据不足时为所有可能的低碳能源转型场景赋予相等的概率。文献[58]指出在缺乏数据的情况下,三角分布能够较好地表示围绕一个给定参数值的对称和不对称变化,文献[36]在分析参数不确定性对英国低碳转型路径的影响时,用三角分布描述各不确定性参数的概率分布。概率的精确值对于分析参数、扰动、行为等不确定性因素的机理并不关键,但对评估其风险则至关重要。

模型的不确定性本质上是因为模型无法反映实际系统,从而给研究结果带来不确定性。对于已经构建的模型,准确性是更适用的评价指标,一般不采用“不确定性的认知程度”对其进行考察。

2 不确定性分析中的典型问题

根据所面临的不确定性因素的差异,所针对的具体分析问题存在差异。若所有因素均是确定性的,则所研究的问题属于给定场景下的确定性分析;若工况/故障/行为的不确定性可由概率分布来描述,则所研究的问题应归结为针对工况/故障/行为不确定性的风险分析。以此类推,若所研究的问题中包括了所有各类不同来源、不同主客观本质、不同认知程度的不确定性因素,则所研究的问题变为针对所有不确定性因素的综合分析。不确定性分析中的典型问题可参见表2。

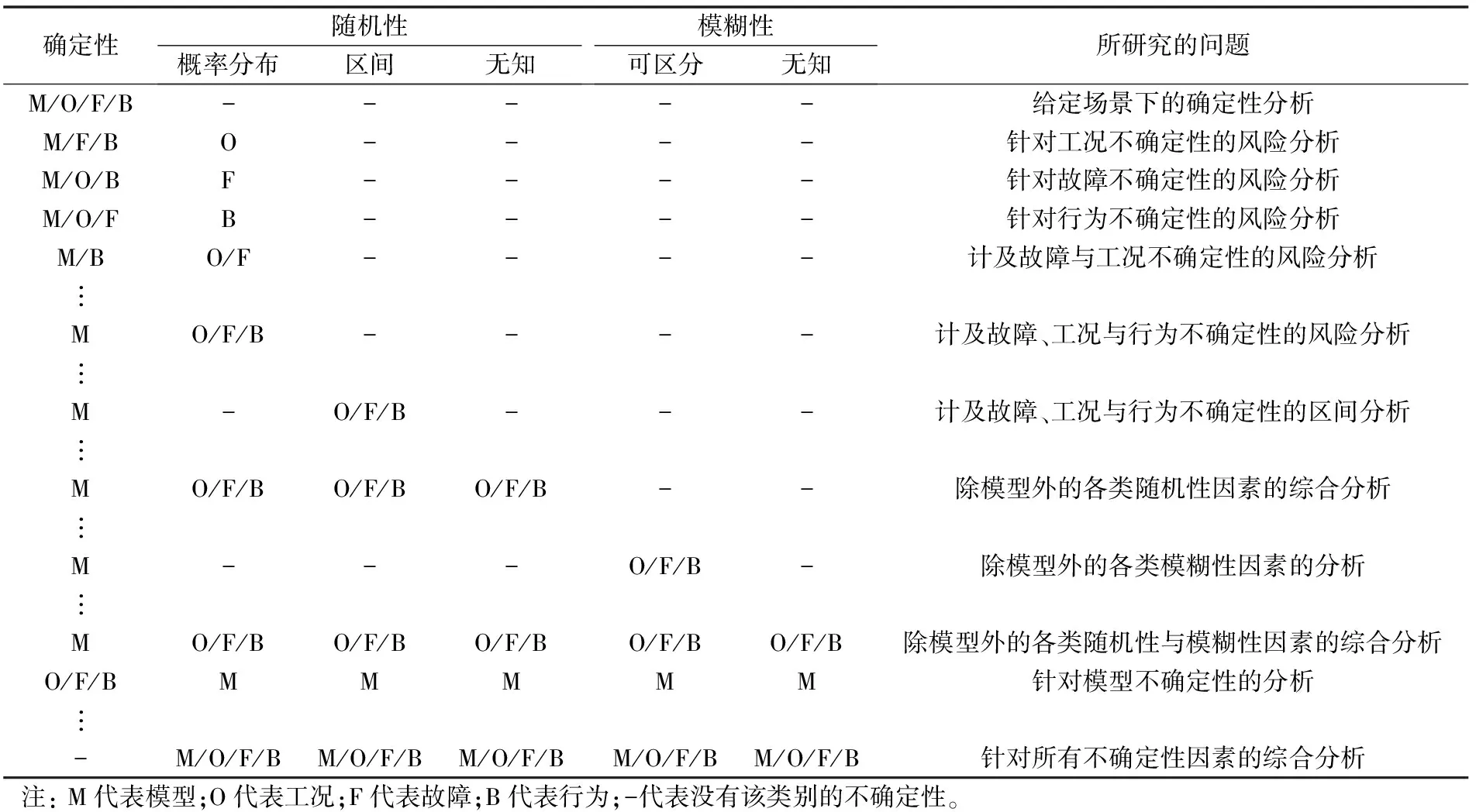
表2 不确定性分析中的典型问题Table 2 Typical research issues in uncertainty analysis

根据所研究问题的差异,需采用不同的分析方法。给定场景下的确定性分析是不确定性分析的基础,需首先解决。随着所考虑不确定性因素的种类和数量的增加,分析的难度也不断增加,针对所有不确定性因素的综合分析的难度最大。不确定性分析方法的关键是识别最重要的不确定性因素并加以分析(即不关注不重要的因素),从而兼顾准确性和计算量。

3 当前的分析方法

3.1 主要方法及其应用范围

表3展示了当前能源转型研究中各类主要不确定性分析方法及其可应对的不确定性。

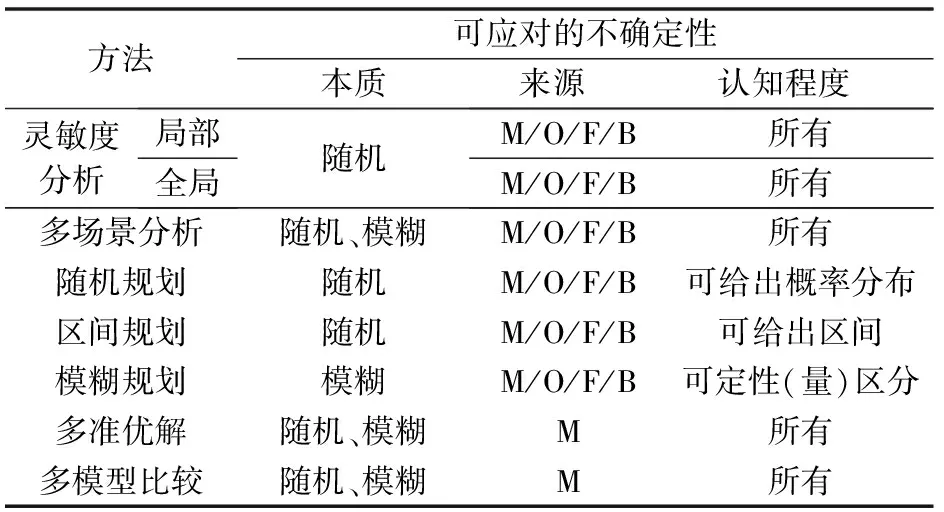
表3 主要分析方法及其可应对的不确定性Table 3 Major analysis approaches and the uncertainties that can be addressed

模糊规划用于研究由模糊性导致的不确定性,通过隶属函数来描述模糊性。区间规划用于数据质量无法达到获取变量概率分布函数的情况,将这些变量处理成简单的区间上下界。区间规划常与模糊规划、最大最小遗憾值规划、随机规划等其他优化理论结合用于应对不确定性[59-60]。两者在能源转型领域的应用仍然较少,后文不做展开。

3.2 灵敏度分析

灵敏度分析是基于确定性模型开展研究时最常用的量化分析参数(可包括模型参数、工况、扰动和行为等,下同)不确定性影响的方法,可分为局部灵敏度分析与全局灵敏度分析[61]。不同认知程度的不确定性因素均可采用灵敏度分析。“解释”是本方法的主要研究目的,也可为“优化”提供灵敏度信息。

局部灵敏度分析是目前应用最广泛的方法,其做法是依次在基准值基础上按指定的目标方向改变目标输入参数值大小(固定其他参数),求取输出参数的变化量,其比值即为指定参数的灵敏度指标值。文献[10]分析了燃料价格、融资成本等不确定性因素对给定的英国电力转型路径评估结果的影响。局部灵敏度分析能够量化输入参数对感兴趣的输出结果的影响,识别出很小的变动就会对输出结果有重大影响的关键性参数,并可按影响程度对参数的重要性进行排序,但不涉及参数变化的概率,也无法计及不同输入参数之间的交互关系[62]。局部灵敏度分析法主要用于参数不确定性,也可用于模型结构的不确定性[24]。

全局灵敏度分析则通过同时改变若干个输入参数值来改进局部灵敏度分析的不足,其分析过程为:先设置待分析参数的概率分布,随后经过大量的抽样仿真(如Monte Carlo法),最后通过统计学方法来开展分析。但本方法的计算量会随着参数数量及其可能的取值个数呈指数级增长[61]。文献[36]基于多元回归分析方法综合分析了各项不确定性参数对英国实现碳减排目标及能源转型总成本的影响,识别出天然气价格和生物质能可获得性是最关键的不确定性参数。

3.3 多场景分析

场景以研究对象的现状为基础,通过一系列具有逻辑和内部一致性的事件序列来描述研究对象未来可能或可以如何演化。由于单个场景无法准确描述或预测未来的情况,需通过多场景分析探寻关于未来的不同可能性,通过透明的定量化方式展示可能的未来场景。

多场景分析方法基于确定性模型针对构建的每个场景进行分析,揭示可能的风险与契机。多场景分析能够应对因随机性和模糊性所导致的工况、扰动和行为方面的不确定性。“解释、预测、推演”是本方法的主要研究目的。若能为各个场景的概率赋值并据此进行风险评估,则多场景分析还可用于不确定性条件下的优化,但目前未见相关报道。

文献[11]的研究中分别为碳价格轨迹、低碳发电技术发展轨迹、消费者心态设置2种可能情况,并据此构建了8种场景。文献[8]的研究中分别为5种低碳技术设置2种可能的发展趋势,并据此构建了32种场景。

亦有研究进行定性化的场景分析,或称为“故事线”(storyline)。但由于故事线易脱离能源转型的实际情况,缺乏可复现性及透明性,将故事线与定量化的仿真模型相结合已经成为新的发展趋势[63]。

对于无法给出概率分布、区间的随机性因素,或者无法定性(量)区分的模糊性因素,多场景分析是最常用的方法。但在设置具体场景时往往缺乏明确的客观依据,具有很强的主观性。

由于研究者往往容易错误估计能源技术突破、重大的政治或社会事件等因素,因此,实际应用中很少出现“出乎意料”的能源转型场景,即分析结果很少超出趋势外推的范畴,从而很难最大限度地探寻未来的不同可能性,容易偏离使用本方法的初衷[24]。

3.4 随机规划

随机规划方法主要用于研究被处理为随机不确定性的因素,通过改变参数取值构建不同的场景并为各场景的发生概率赋值,在不确定性条件下得到满足其优化目标(一般取为期望经济代价最小)的转型决策。使用随机规划方法时,需给出随机因素的概率分布。

各研究中所采用的随机规划模型大多属于MARKAL/TIMES系列,如UK-MARKAL[12]，Danish TIMES[64]，TIAM-World(TIMES integrated assessment model)[65]。

文献[12]根据英国政策制定者所关注的不确定性因素以及文献[66]中所识别的关键性不确定性因素,分别针对燃料价格和生物质能进口量的不确定性优化能源转型决策。但该研究所针对的两项不确定性因素未经过严格的重要性排序，影响了能源转型优化决策的有效性。

基于随机模型开展的研究中所计及的不确定因素还包括风电的间歇性与电力价格随机性的联合影响[64]、技术进步[65]、能源价格[67]等。

随机规划模型受限于“维数灾”问题,一般仅考虑少量的不确定性因素。

3.5 多准优解

多准优解法,也被称为MGA(modeling to generate alternatives)法,用于应对模型不确定性。其基本思想是:由于能源转型优化模型很难计及政治可行性、社会公平等政策制定者非常重视的因素,因此,优化模型求取的单个最优解往往不是实际决策中采用的转型方案,理想的方案更可能位于解空间中的其他区域[9]。该方法基于一定的规则在最优解的基础上通过人为增加松弛量等方式修改优化模型的目标函数和约束条件,求取一组可行的但在结构上与最优解有着很大差异的准最优解作为备选。产生准最优解的常用方法有双重描述(double description)法[68]、Hop-Skip-Jump方法[69]等。

模型的使用者(一般是政策制定者)将所有备选准最优解间重叠的部分作为必须实施的决策(must-haves)、均未包括的部分作为必须避免的决策(must-avoids)、差异部分则作为需要进一步仔细研究的决策(real choices)[70]。

该方法的局限性包括:松弛量的设定具有主观性,且对结果有重大影响;不同于灵敏度分析和多场景分析方法,无法获取参数变化对输出结果的影响,直观性差;无法针对生成的不同备选解给出概率信息。因此,更为可行的做法是将该方法视作现有方法的补充,用于校验现有不确定性条件下优化方案的鲁棒性[9]。

3.6 多模型比较

基于不同能源模型的结果之间可能存在非常大的差异。多模型比较法能够得到针对相同场景的多个不同的解,并据此识别出多个解中的共性,鉴别输入参数、模型差异与输出结果的差异之间的关系。

能源与环境领域的多模型比较始于由斯坦福大学于1976年发起的Energy Modelling Forum(EMF),到目前为止已经进行了共计34个国际性的项目,涉及的议题包括:电力、石油、煤炭、天然气、能源效率、气候变化等[15]。类似的项目还包括欧盟的AMPERE[71],亚洲的AME[72]等。

然而,这些模型间的比较研究仅关注如何识别不同模型间的差异,而不关注如何评估和改进单个模型在结构上的不确定性。

近年来,出现了一些讨论应对模型结构不确定的研究,但相比更为成熟的参数不确定性分析方法,这些方法仍有待实际复杂问题的检验[73]。

3.7 行为不确定性的分析方法

长期以来,能源转型政策依赖于能源、工程、经济等领域的跨学科合作,但与社会学、政治学、心理学等其他学科合作以更好地分析参与者行为则一直处于主流研究之外或仅作为给定的假设条件(如“理性选择”[74]),而试图讨论或反思与行为不确定性相关的政策失灵的研究则往往遭遇更大的阻力[75]。

目前的研究中共有3类计及行为的方法:①涵盖参与者行为的能源转型故事线;②建立参与者的行为模型;③真实人参与仿真。

能源转型故事线由关键性参与者共同讨论形成,定性地界定了技术—经济仿真需遵循的场景。行为的不确定性体现为形成多条存在差异的故事线,但在该方法下人的行为不与技术—经济模型发生动态交互。

参与者的行为模型可与技术—经济模型进行动态交互仿真,允许不同参与者的行为偏好存在差异,但在整个仿真过程中每个参与者的行为偏好均是确定的。文献[75]基于名为BLUE的技术—经济—行为模型,比较了三类碳排放价格政策场景(高、中、低),以及三类不同的参与者决策行为模式(对新技术成本差异以及先期投资的敏感性不同)所驱动的9个能源转型场景,分析了非理性行为的影响。

基于实验经济学的方法论,将能源转型问题中的客观能源系统、外部环境等能够用数学模型表达的环节构成客观实验环境,由真实实验人与实验环境进行互动,行为不确定性的影响便可反映在实验结果之中。但真实人参与仿真也带来了新的挑战,例如,分析参数灵敏度或搜索优化解时必然需要进行反复仿真,但是,一方面难以长期占用大量合格的真实人参与仿真,另一方面真实人难以保证在反复仿真中保持态度与偏好的“一致性”(coherent),从而影响灵敏度分析结果的可比性或优化的收敛性。

文献[5]结合计算经济学与实验经济学的优点,提出了一种融合技术—经济—行为统计学模型—真实参与者的混合仿真方法。由于融合了行为统计学模型与真实参与者,故能够更好地反映能源转型中关键性利益相关者的决策行为。其中,行为模型的建立基于对行为数据的挖掘分析,并确保模型的输出与特定参与者群体的行为在统计学上保持一致。为此,尽管在每次具体仿真中单个参与者的行为模式存在不确定性,但整个群体行为的概率分布是确定的,从而可以用代理模型代替大量真实参与者的行为,开展反复的实验经济学仿真[76]。

此外,由于能源转型涉及的时间尺度长达几十年,参与者的行为模式极可能随时间发生变化,故还需对群体行为的概率分布随时间的变化开展研究。

4 建议的综合分析框架

上文所介绍的各类分析方法的适用范围均局限于某些类型的不确定性因素。在面对大量特点各异的不确定性因素时,无法兼顾分析的精度与速度。

图1描述了本文所建议的针对各类不确定性因素在来源、主客观本质、认知程度等方面的不同特点,融合多种分析方法的不确定性综合分析框架。主要包括以下部分。

1)按特点对不确定性因素归类。针对待分析的不确定性因素,依次按照其在来源、本质、认知程度方面的特点进行归类。模型不确定性直接基于多准优解(3.5节)和多模型比较法(3.6节)进行分析。模型参数、工况、扰动、行为(观点体现在行为中)的不确定性按其本质被归为随机性或模糊性。随机性按认知程度被分为可给出概率分布、可给出区间以及(意识到的)无知。模糊性按认知程度被分为可定性(量)区分以及无知,其中前者可通过模糊数学等各种分析工具进行分析,后文不做展开。

2)期望工况下的随机性因素筛选。基于期望工况,针对可给出概率分布的随机性因素进行单因素的快速风险评估,并根据设置的风险阈值将其区分为高风险和低风险;针对可给出区间的随机性因素进行单因素的敏感性分析,并根据主观设置的阈值将其区分为高敏感性和低敏感性。由于因素数量较多,本阶段将采用尽量简单的模型以减少计算量。

高风险因素将用于后续的风险优化;低风险因素将用于优化方案的风险校核;高敏感性因素将用于优化方案的强壮性校核;低敏感性因素则被归为非关键性因素而无需开展后续分析。

筛选过程为后续分析环节保留了关键性因素以顾及准确性,由于无需再处理非关键性因素从而大大减少了计算量。风险或敏感性阈值的设置带有主观性,实际分析中按对于优化效果和计算量的偏好来选取阈值。阈值越高,则形成的有代表意义的确定性场景数量越少,故计算量越小,但优化效果变差。

3)多不确定性因素下的风险优化。包括以下3个子任务:①基于高风险因素形成有代表意义的确定性场景并计算其所反映的概率;②计算各确定性场景下所关心的能源转型方案的评估指标;③基于风险的评估结果聚合或能源转型方案优化;其中,任务1和3紧密相关,任务2是与不确定性相对独立的确定性分析问题。

在任务3中若仅用各场景发生的概率(而不计及转型代价)对评估结果加权统计,则退化为概率性分析,仅能考虑能源转型方案下实现所关心指标(如清洁能源占比发展目标或碳减排目标)的概率,无法反映能源转型方案的风险代价。对于能源转型优化问题,概率指标仅能作为约束条件,无法协调经济性和清洁性(或低碳性)。基于风险代价的优化则同时包含了能源转型对清洁性和经济性的要求,可以协调经济性和清洁性。

文献[77]指出由于模型与参数不确定性同时存在以及很多参数无法做出可信的描述,将经济代价最优作为研究目标所得到的结果往往与现实中的能源转型状况相去甚远。然而,上述批评并不能否定转型方案优化能够对政策与战略的制定提供最重要的支撑作用,也无法否定随机规划等优化算法本身的价值。所需要改进的是通过进一步的研究来努力改进对不确定性信息的掌握程度,以及在形成用于方案优化的场景时格外慎重以避免使用不可靠的信息。

对于发生概率很小(往往意味着很难准确估计其概率)但代价很大的扰动事件,也应该尝试给出概率的大概范围、即使仅是数量级尺度的估计,并据此开展风险分析。类似的尝试均有利于提高研究价值,改进对转型决策的支撑。

筛选后的场景数量已经有效减少,故本阶段的分析中可采用较为详细的模型,以提高分析的准确性。但能源转型优化是典型的非线性问题,其优化过程往往需要大量的迭代,考虑到计算速度方面的约束,仍不应采用过于详细的模型。

4)针对优化方案的风险校核与强壮性校核。由于待校核优化方案可能与期望工况有很大的差异,在低风险因素所形成的某些校核场景下,该方案的风险可能超过风险阈值,故应考虑将该部分场景加入风险优化的场景集中,并重新优化方案,重复上述迭代过程直至所有高风险场景均已被计及。作为分析的最后一个阶段,应尽可能采用最详细的模型以准确评估待校核优化方案。

本分析框架中,依次针对经筛选后的高风险、低风险、高敏感性因素进行分析,在每个环节均将其他不确定性因素处理为确定值(期望值、中值、或明晰量等),从而有效减少了每个环节因不确定性因素数量过大所导致的计算量负担。通过逐渐详细化的模型,以保证分析结果的准确性。

值得指出的是,并非所有的不确定性分析均需包括上述所有环节。例如,若需回答“某参数取值的不确定性将如何影响给定的能源转型方案的经济代价?”,则仅需采取灵敏度分析或多场景分析即可完成分析任务。

5 结语

能源转型分析是一类面临大量不确定性因素的复杂问题。一方面,不确定性因素在来源、主客观本质、认知程度三个方面存在差异,不可能采用某种单一的分析方法来应对所有的不确定性因素。另一方面,不确定性因素数量庞大,若在分析时遍历所有的可能情况会面临场景数量的组合爆炸。现有的各类分析方法均未能有效应对上述挑战。

本文所提出的综合分析框架中针对随机性与模糊性分别选取不同的分析方法。针对不同特点的大量随机性因素,先后通过基于简单模型的关键性因素筛选、较详细模型的风险优化以及详细模型的强壮性校核,兼顾了分析结论的计算量与准确性。针对模糊性则根据其是否可定性或定量地区分而采用模糊集理论等多种方法进行分析。

能源转型涉及领域非常广、数据需求特别大,但研究者能够掌握的往往只是很少一部分可供研究的信息,尤其是关于未来的信息。增加实证研究可获取更多信息,但不确定性不可能被完全消除。在信息不完备的情况下,结合有效合理的假设,基于本文所提出的综合分析框架仍可提升研究结论的价值、增强对政策或战略决策的支撑能力。

本系列文章讨论了能源转型分析的要素、研究范式、不确定性等方面,详细的研究仍在进行。

参 考 文 献

[1] ROWE W D. Understanding uncertainty [J]. Risk Analysis, 1994, 14(5): 743-750.

[2] VAN ASSELT M, ROTMANS J. Uncertainty in integrated assessment modelling: from positivism to pluralism [J]. Climatic Change, 2002, 54(1/2): 75-105.

[3] ROCQUIGNY E, NICOLAS D, STEFANO T. Uncertainty in industrial practice: a guide to quantitative uncertainty management[M]. Chichester, UK: John Wiley&Sons, Ltd, 2008.

[4] 鞠平,刘咏飞,薛禹胜,等.电力系统随机动力学研究展望.[J].电力系统自动化,2017,41(1):1-8.DOI:10.7500/AEPS20160530011.

JU Ping, LIU Yongfei, XUE Yusheng, et al. Research prospects for stochastic dynamics of power system[J]. Automation of Electric Power Systems, 2017, 41(1): 1-8. DOI: 10.7500/AEPS20160530011.

[5] XUE Y S, YU X H. Beyond smart grid—a cyber-physical-social system in energy future[J]. Proceedings of the IEEE, 2017, 105(12): 2290-2292.

[6] 舒印彪,薛禹胜,蔡斌,等.关于能源转型分析的评述:(一)转型要素与研究范式[J].电力系统自动化,2018,42(9):1-15.DOI:10.7500/AEPS20180417008.

SHU Yinbiao, XUE Yusheng, CAI Bin, et al. A review of energy transition analysis: elements and paradigms[J]. Automation of Electric Power Systems, 2018, 42(9): 1-15. DOI: 10.7500/AEPS20180417008.

[7] PFENNINGER S, HAWKES A, KEIRSTEAD J. Energy systems modeling for twenty-first century energy challenges[J]. Renewable and Sustainable Energy Reviews, 2014, 33(2): 74-86.

[8] FAIS B, KEPPO I, ZEYRINGER M, et al. Impact of technology uncertainty on future low-carbon pathways in the UK[J]. Energy Strategy Reviews, 2016, 13-14: 154-168.

[9] DECAROLIS J F. Using modeling to generate alternatives (MGA) to expand our thinking on energy futures[J]. Energy Economics, 2011, 33(2): 145-152.

[10] TRUTNEVYTE E, STRACHAN N, DODDS P E, et al. Synergies and trade-offs between governance and costs in electricity system transition[J]. Energy Policy, 2015, 85: 170-181.

[11] YÜCEL G, VAN DAALEN C. A simulation-based analysis of transition pathways for the Dutch electricity system[J]. Energy Policy, 2012, 42: 557-568.

[12] USHER W, STRACHAN N. Critical mid-term uncertainties in long-term decarbonisation pathways[J]. Energy Policy, 2012, 41: 433-444.

[13] SADEGHI M, HOSSEINI H M. Energy supply planning in Iran by using fuzzy linear programming approach regarding uncertainties of investment costs[J]. Energy Policy, 2006, 34(9): 993-1003.

[14] DONG C, HUANG G H, CAI Y P, et al. An interval-parameter minimax regret programming approach for power management systems planning under uncertainty[J]. Applied Energy, 2011, 88: 2835-2845.

[15] Stanford University. Energy modeling forum[EB/OL]. [2017-12-20]. https://emf.stanford.edu/projects.

[16] VAN DER SLUIJS J P, JANSSEN P H M, PETERSEN A C, et al. RIVM/MNP guidance for uncertainty assessment and communication: tool catalogue for uncertainty assessment[EB/OL]. [2017-12-20]. http://www.nusap.net/downloads/toolcatalogue.pdf.

[17] REFSGAARD J C, VAN DER SLUIJS J P, HØJBERG A L, et al. Harmoni-CA guidance: uncertainty analysis[EB/OL]. [2017-12-20]. http://www.harmoni-ca.info/toolbox/docs/Harmoni-ca_Guidance_1_Uncertainty_Analysis.pdf.

[18] MIRAKYAN A, DE GUIO R. Modelling and uncertainties in integrated energy planning[J]. Renewable and Sustainable Energy Reviews, 2015, 46: 62-69.

[19] MORET S, CODINA G V, BIERLAIRE M, et al. Characterization of input uncertainties in strategic energy planning models[J]. Applied Energy, 2017, 202: 597-617.

[20] GLEICK J. Chaos: making a new science[M]. Penguin, London, UK. 1989.

[21] STEWART I. Does God play dice? the mathematics of chaos[M]. London, UK: Blackwell. 1989.

[22] SUGIHARA G, GRENFELL B, MAY R M, et al. Distinguishing error from chaos in ecological time[J]. Philosophical Transactions of the Royal Society London, Series B: Biocogical Sciences, 1990, 330(25): 235-251.

[23] WALKER W E, HARREMOES P, ROTMANS J, et al. Defining uncertainty: a conceptual basis for uncertainty management in model-based decision support [J]. Integrated Assessment, 2003, 4(1): 5-17.

[24] SKINNER D J C, ROCKS S A, POLLARD S J T, et al. Identifying uncertainty in environmental risk assessments: the development of a novel typology and its implications for risk characterization[J]. Human and Ecological Risk Assessment, 2014, 20(3): 607-640.

[25] DAVIES G, PRPICH G, STRACHAN N, et al. UKERC energy strategy under uncertainties: identifying techniques for managing uncertainty in the energy sector, working paper[EB/OL]. [2017-12-20]. http://ukerc.rl.ac.uk/UCAT/PUBLICATIONS/Identifying_Techniques_Managing_Uncertainty_Energy_Sector_Working_Paper.pdf.

[26] BAECHER G B, CHRISTIAN J T. Natural variation, limited knowledge, and the nature of uncertainty in risk analysis[C]// Proceedings of the 19th united engineering foundation conference on risk-based decision-making in water resources, October 15-20, 2000, Santa Barbara, US.

[27] 薛禹胜,雷兴,薛峰,等.关于风电不确定性对电力系统影响的评述[J].中国电机工程学报,2014,34(29):5029-5040.

XUE Yusheng, LEI Xing, XUE Feng, et al. A review on impacts of wind power uncertainties on power systems [J]. Proceedings of the CSEE, 2014, 34(29): 5029-5040.

[28] 李德毅,刘常昱,杜鹢,等.不确定性人工智能[J].软件学报,2004,15(11):1583-1594.

LI Deyi, LIU Changyu, DU Yi, et al. Artificial intelligence with uncertainty[J]. Journal of Software, 2004, 15(11):1583-1594.

[29] 刘宝旋,彭锦.不确定理论教程[M].北京:清华大学出版社,2005.

[30] REGAN H M., COLYVAN M, BURGMAN M A. A taxonomy and treatment of uncertainty for ecology and conservation biology[J]. Ecological Applications, 2002, 12(2): 618-628.

[31] ASCOUGH J C , MAIER H R, RAVALICO J K, et al. Future research challenges for incorporation of uncertainty in environmental and ecological decision-making [J]. Ecological Modelling, 2008, 219(3/4): 383-399.

[32] NORTON J P, BROWN J D, MYSIAK J. To what extent, and how, might uncertainty be defined? comments engendered by “defining uncertainty: a conceptual basis for uncertainty management in model-based decision support”[J]. Integrated Assessment, 2006, 6(1): 83-88.

[34] DANTZIG G B. Linear programming under uncertainty[J]. Management Science, 1955, 1(3/4): 197-206.

[35] TOCK L, MARÉCHAL F. Decision support for ranking Pareto optimal process designs under uncertain market conditions[J]. Computers and Chemical Engineering, 2015, 83: 165-175.

[36] PYE S, SABIO N, STRACHAN N. An integrated systematic analysis of uncertainties in UK energy transition pathways[J]. Energy Policy, 2015, 87: 673-684.

[37] ZADEH L A. Fuzzy sets[J]. Information and Control. 1965, 8: 338-353.

[38] PAWLAK Z I. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(8): 41-356.

[39] DUBOIS D. Possibility theory and statistical reasoning[J]. Computational Statistics & Data Analysis, 2006, 51(1): 47-69.

[40] SHAFER G. A mathematical theory of evidence[M]. New Jersey, US: Princeton University Press, 1976.

[41] BEN-HAIM Y. Info-gap decision theory: decisions under severe uncertainty[M]. 2nd ed. Oxford, UK: Academic Press, 2006.

[42] MOORE R E, KEARFOTT R B, CLOUD M J. Introduction to interval analysis[M]. Philadelphia, US: Society for Industrial and Applied Mathematics, 2009.

[43] BAUDRIT C, COUSO I, DUBOIS D. Joint propagation of probability and possibility in risk analysis: towards a formal framework[J]. International Journal of Approximate Reasoning, 2007, 45(1): 82-105.

[44] HE Y Y, MIRZARGAR M, KIRBY R M. Mixed aleatory and epistemic uncertainty quantification using fuzzy set theory[J]. International Journal of Approximate Reasoning, 2015, 66: 1-15.

[45] DER KIUREGHIAN A, DITLEVSEN O. Aleatory or epistemic? does it matter?[J]. Structural Safety, 2009, 31: 105-112.

[46] USHER W, STRACHAN N. An expert elicitation of climate, energy and economic uncertainties[J]. Energy Policy, 2013, 61: 811-821.

[47] MORGAN M G, KEITH D W. Improving the way we think about projecting future energy use and emissions of carbon dioxide[J]. Climatic Change, 2008, 90(3): 189-215.

[48] STIRLING A. Science, precaution, and the politics of technological risk: converging implications in evolutionary and social scientific perspectives[J]. Annals of the New York Academy of Sciences, 2008, 1128: 95-110.

[49] The Core Writing Team, PACHAUR R K, MEYER L. Climate change 2014: synthesis report[R]. Geneva, Suitzerland: IPCC, 2014: 151p.

[50] THALER R. Toward a positive theory of consumer choice[J]. Journal of Economic Behavior and Organization, 1980, 1(1): 39-60.

[51] THALER R. Mental accounting matters[J]. Journal of Behavioral Decision Making, 1999, 12(3): 183-206.

[52] The Royal Swedish Academy of Sciences. Richard H. Thaler: integrating economics with psychology[EB/OL]. [2017-12-10]. https://www.nobelprize.org/nobel_prizes/economic-sciences/laureates/2017/advanced-economicsciences2017.pdf.

[53] 薛禹胜,赖业宁.大能源思维与大数据思维的融合:(一)大数据与电力大数据[J].电力系统自动化,2016,40(1):1-8.DOI:10.7500/AEPS20151208005.

XUE Yusheng, LAI Yening. Integration of macro energy thinking and big data thinking: part one big data and power big data[J]. Automation of Electric Power Systems, 2016, 40(1): 1-8. DOI: 10.7500/AEPS20151208005.

[54] WILKINSON N, KLAES M. An introduction to behavioral economics, second edition[M]. London, UK: Palgrave Macmillan, 2012.

[55] XUE Y S, WU J, XIE D L, et al. Multi-agents modelling of EV purchase willingness based on questionnaires[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(2): 149-159.

[56] MORRIS C, PEHNT M. Energy transition: The German energiewende[EB/OL]. [2017-12-10]. https://book.energytransition.org/sites/default/files/etbook/v2/en/German-Energy-Transition_en.pdf.

[57] LOULOU R, LABRIET M, KANUDIA A. Deterministic and stochastic analysis of alternative climate targets under differentiated cooperation regimes[J]. Energy Economics, 2009, 31(2): S131-S143.

[58] BIEGLER L, BIROS G, GHATTAS O, et al. Large-scale inverse problems and quantification of uncertainty[M]. Chichester, UK: John Wiley and Sons, 2011.

[59] HU Q, HUANG G H, CAI Y P, et al. Feasibility-based inexact fuzzy programming for electric power generation systems planning under dual uncertainties[J]. Applied Energy, 2011, 88: 4642-4654.

[60] LI Y F, LI Y P, HUANG G H, et al. Energy and environmental systems planning under uncertainty-an inexact fuzzy-stochastic programming approach[J]. Applied Energy, 2010, 87: 3189-3211.

[61] SALTELLI A, RATTO M, ANDRES T, et al. Global sensitivity analysis: the primer[M]. Chichester, England: John Wiley&Sons, 2008.

[62] SALTELLI A, ANNONI P. How to avoid a perfunctory sensitivity analysis[J]. Environmental Modelling&Software, 2010, 25(12): 1508-1517.

[63] TRUTNEVYTE E, BARTON J, O’GRADY, et al. Linking a storyline with multiple models: a cross-scale study of the UK power system transition[J]. Technological Forecasting&Social Change, 2014, 89: 26-42.

[64] SELJOM P, TOMASGARD A. Short-term uncertainty in long-term energy system models-a case study of wind power in Denmark[J]. Energy Economics, 2015, 49: 157-167.

[65] LABRIET M, KANUDIA A, LOULOU R. Climate mitigation under an uncertain technology future: a TIAM-World analysis[J]. Energy Economics, 2012, 34 (3): S366 - S377.

[66] USHER W, STRACHAN N. UK MARKAL modelling-examining decarbonisation pathways in the 2020s on the way to meeting the 2050 emissions target[EB/OL]. [2017-12-20]. http://downloads.theccc.org.uk.s3.amazonaws.com/4th Budget/CCC MARKAL Final Report - UCL Nov10.pdf.

[67] KREY V, MARTINSEN D, WAGNER H. Effects of stochastic energy prices on long term energy-economic scenarios[J]. Energy, 2007, 32 (12): 2340-2349.

[68] TRUTNEVYTE E. EXPANSE methodology for evaluating the economic potential of renewable energy from an energy mix perspective[J]. Applied Energy, 2013, 111: 593-601.

[69] BRILL E D, CHANG S, HOPKINS L D. Modeling to generate alternatives: the HSJ approach and an illustration using a problem in land use planning[J]. Management Science, 1982, 28(3): 221-235.

[70] VOLL P, JENNINGS M, HENNEN M, et al. The optimum is not enough: a near-optimal solution paradigm for energy systems synthesis[J]. Energy, 2015, 82: 446-456.

[71] KRIEGLER E, RIAHI K, BAUER N, et al. Making or breaking climate targets: the AMPERE study on staged accession scenarios for climate policy[J]. Technological Forecasting and Social Change, 2015, 90: 24-44.

[72] CALVINA K, CLARKEA L, KREY V, et al. The role of Asia in mitigating climate change: results from the Asia modeling exercise[J]. Energy Economics, 2012, 34(3): 251-260.

[73] REFSGAARD J C, VAN DER SLUIJS J P, BROWN J, et al. A framework for dealing with uncertainty due to model structure error[J]. Advances in Water Resources, 2006, 29(11): 1586-1597.

[74] SOVACOOL B K. What are we doing here? analyzing fifteen years of energy scholarship and proposing a social science research agenda[J]. Energy Research&Social Science, 2014, 1: 1-29.

[75] LI F G N. Actors behaving badly: exploring the modelling of non-optimal behaviour in energy transitions[J]. Energy Strategy Reviews, 2017, 15: 57-71.

[76] 薛禹胜, 赖业宁.大能源思维与大数据思维的融合:(二)应用及探索[J].电力系统自动化,2016,40(8):1-13.DOI:10.7500/AEPS20160311004.

XUE Yusheng, LAI Yening. Integration of macro energy thinking and big data thinking: part two applications and explorations[J]. Automation of Electric Power Systems, 2016, 40(8): 1-13. DOI: 10.7500/AEPS20160311004.

[77] TRUTNEVYTE E. Does cost optimization approximate the real-world energy transition?[J]. Energy, 2016, 106: 182-193.