基于PSO-BP预测模型的盾构机密封舱土压平衡控制
2018-05-23李景轩
李 强,李景轩
(西安理工大学 自动化与信息工程学院,陕西 西安 710048)
0 引言
盾构机是一种集电气、机械、液压、测量及控制等多学科技术于一体的大型电液设备,专门应用于地下隧道工程,它具有施工速度快、自动化程度高、安全性高、对地面建筑影响小、对环境影响小等优点。在盾构的掘进过程中,维持密封舱土压平衡是非常重要的。掘进时,为了减少对土体造成的扰动、防止因为地表变形而引起灾难性事故的发生,必须对密封舱土压进行准确的控制,保持开挖面的压力平衡。由于传统的司机控制模式具有一定的滞后性,如何准确预测及控制密封舱土压成为了盾构掘进领域的一个热点[1-3]。密封舱压力平衡的控制是多变量控制,需要综合考虑刀盘、推进系统和螺旋输送机等因素的影响。实际中,维持密封舱土压平衡主要凭借操作者的经验去调节螺旋输送机转速或推进速度,尚未实现该过程自动控制[4]。因此,已有学者对此展开了深入研究。文献[5]基于盾构掘进的原理,对掘进过程的数学物理参数进行了分析,初步建立了盾构掘进的物理模型。文献[6]采用神经网络的方法对密封舱土压建立预测模型。文献[7]采用自适应神经网络模糊推理(ANFIS)的方法对密封舱土压进行的预测,但是此类方法学习收敛速度慢,容易陷入局部最优,实时的学习能力和泛化能力较差。为了得到更加准确的密封舱土压和施工参数之间的关系,文献[8]利用小型盾构机模型进行了实验研究,得到了密封舱压力、总推进力、螺旋输送机转速以及刀盘扭矩等参数之间的关系。
由于盾构机的推进速度受到密封舱土压、顶进油缸扭矩、推力等多方面因素的影响,推进速度的改变必然会连带影响其他参数。因此,本文综合考虑了刀盘扭矩对密封舱压力的影响,首先基于PSO-BP算法建立了密封舱土压预测模型,提前一步预测下一时刻的土压,然后结合PSO算法得到最优的螺旋输送机转速,作用于密封舱土压平衡的控制过程,有效提高了控制的精度。
1 盾构掘机理模型描述
1.1 盾构掘进过程的连续性方程
在盾构机掘进过程中,假设各组油缸推进推力和刀盘转速不变,且盾构机没有出现超推进和欠推进状态,则盾构机处于正常稳定掘进状态,刀盘切削进入密封舱的原状土量和排出量相等,则盾构处于土压平衡状态,此时密封舱进土量为:
Vi=πR2ΔS
(1)
其中:Vi为盾构机推进ΔS距离应排除的原状土体积;R为刀盘半径。
螺旋输送机出土量的控制是维持土压平衡盾构机土压平衡的关键,螺旋输送机出土量与转速的关系为:
Q0=ηANL
(2)
(3)
其中:Qo为螺旋输送机排土量;η为排土效率;A为螺旋输送机有效断面积;N为螺旋输送机转速;L为螺旋输送机叶片间距;D1为螺旋输送机直径;D2为螺旋输送机轴直径。
ΔT时间内螺旋输送机的出土量为:
dG=ηANLdT
(4)
其中:dG为单位时间内螺旋输送机排土量。
在盾构的施工过程中,为了改良土质,会在密封舱中加入添加剂对渣土进行塑化处理。考虑添加剂重量,则有效土比为:
(5)
其中:dG天然为单位时间内排出的天然土重量,计算公式如式(6)所示;dG添加为单位时间内排出的添加剂重量。
dG天然=KeηANLdT
(6)
若γ0为天然土容重,则dT时间内排出的天然土体积为:
(7)
密封舱内渣土流量连续性方程[7]为:
(8)
其中,cep为土仓外部泄露系数;pe为土仓内土压力;po为土仓外泄露压力,po≈0;ve为土仓容积;βe为土仓土料、液体、气体的有效压缩系数;Vi和V天然分别为密封土仓渣土的进入和出土量。
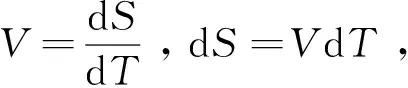
(9)
1.2 土压和推力及刀盘转速的关系
以整个盾构机为研究对象,有力学方程:
F-f-P=ma
(10)
其中:F为盾构机推进油缸所提供的总推力;f为推进时总阻力;P为刀盘和开挖面土体接触压力;m为盾构机总质量;a为盾构机推进加速度。由于盾构机推进速度较为缓慢,故认为盾构机加速度a为零。故有下式:
F=f+P
(11)
其中总阻力f包括:盾构侧面与周边地层的摩擦阻力;刀具贯入土体所受到的抵抗力;盾构姿态调整或者曲线施工的附加阻力;盾体和管片之间的摩擦力;后配套设备的牵引力。
另外,对于面板式盾构机,其面板上的土压力要比土压仓压力大一个附加值δ,故有下式:
(12)
其中:λ为刀盘开口率;其他符号意义同上。将式(12)代入(11)可以得到土压和推力的关系:
(13)
将式(13)做如下转换可以得到:
(14)
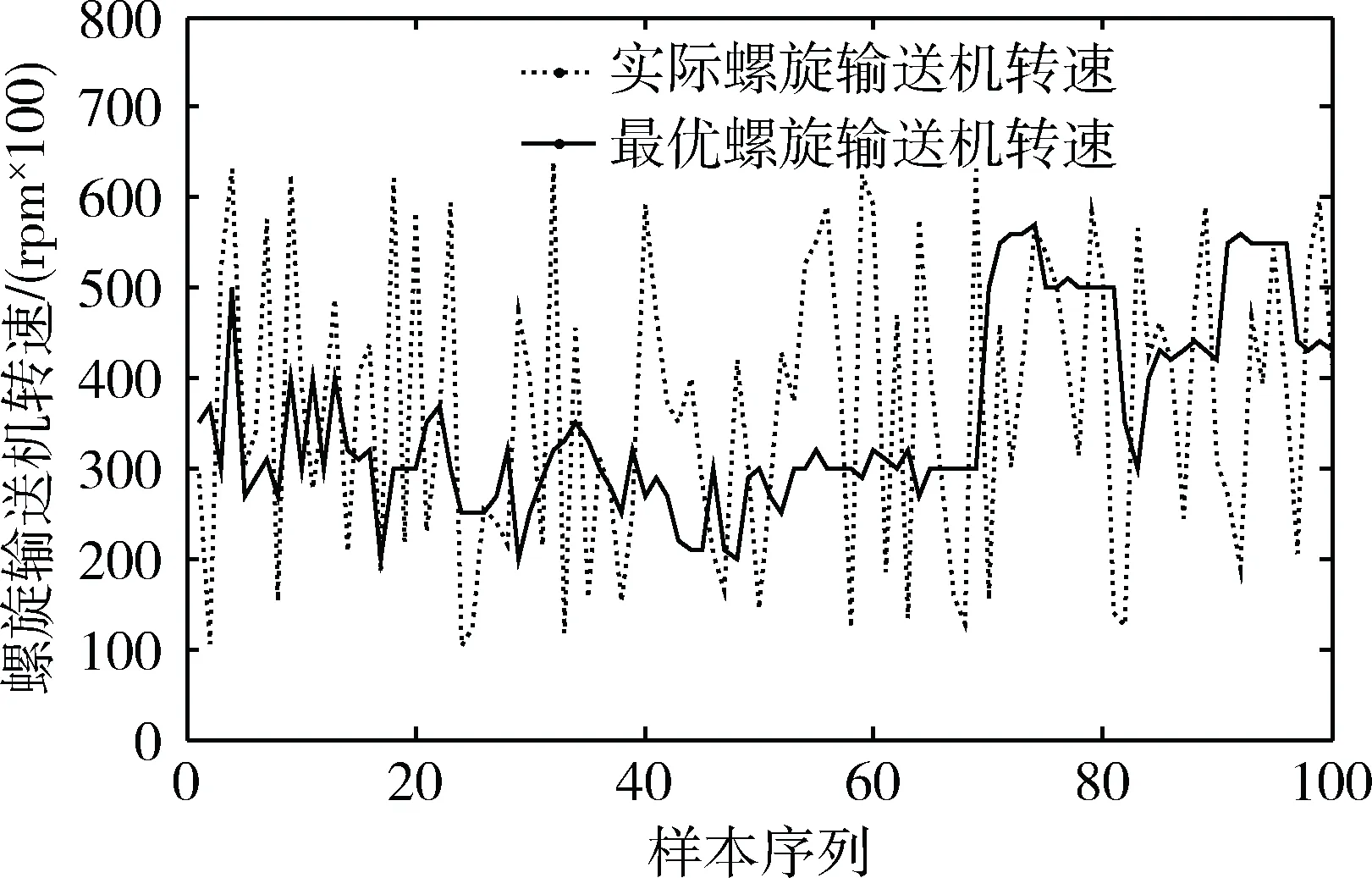
刀盘实际作用的土压为P,且有:主动压力 因为刀盘上面土压力分布的状态很有可能会因为开挖面的局部坍塌而变化,所以P可以用下式表示[9]: (15) p′和q′分别是从刀盘中心沿p轴和q轴到刀盘上一个点所测量到的距离与刀盘的半径R的比值;n为刀盘旋转速度;r为刀盘上计算点的半径;σno是法向静止土压力,计算公式如式(16)所示;a、b为常数,这两个值的范围为-1~1;F(p′)和F(q′)分别为土压沿p轴和q轴变化的状态因数。 σno=Kσvo (16) 其中,K为侧向土压力系数。初始垂直土压力σvo为(对于粘性土壤): σvo=(Hc+rcosθ)γ (17) 其中:Hc为地面到盾构机轴线的距离;θ为任意方向;r为刀盘上点到中心距离;γ为土的重度。 对于粘性土刀盘水平土压力计算公式为: (18) 将式(18)和式(13)带入式(11)可得: δ(1-λ) (19) 式(19)即为土压与刀盘转速关系式。 刀盘扭矩是盾构机掘进过程中的一个重要参数,是保证盾构正常掘进、安全运行的关键参数之一。当盾构机推进速度过快或推进压力过大时会导致刀盘扭矩的急剧上升,此时会造成密封舱土压的相应增大,导致刀盘卡死甚至刀盘损坏。刀盘扭矩主要包括摩擦扭矩、切削扭矩和搅拌扭矩,文献[10]从影响刀盘扭矩因素的角度给出刀盘扭矩切削关系表达式: (20) 其中,Tn为刀盘切削扭矩;φ为土体内摩擦角;C为切削面土体的粘聚力。从式(12)和式(20)可以得出刀盘扭矩和密封舱土压的关系,表明了刀盘扭矩会对密封舱土压产生影响。文献[8]指出了影响刀盘扭矩的主要因素是盾构面板和开挖面土体的接触压力即刀盘面板土压,并通过拟合刀盘扭矩和密封舱土压的关系证明了这一点。但是在实际中单纯通过数学物理推导刀盘扭矩和密封土仓压力之间的关系比较困难,因此文献中给出了刀盘扭矩和密封舱土压以及刀盘转速之间的关系表达式: M=kcnPe (21) 式中:M为刀盘扭矩;kc为与刀盘形式、土体有关的参数。 通过上述分析可知盾构密封舱土压与盾构推进速度、总推进力、螺旋输送机转速以及刀盘扭矩之间具有非线性的耦合关系,当前土压可表示为:Pe=f(V,F,N,M)。 由于盾构掘进过程是一个复杂、非线性、多变量且掘进参数之间具有强耦合性的工业对象,较难有效辨识出机理模型参数,因此,本文采用PSO-BP算法来实现盾构机密封舱土压的预测。 由于BP神经网络存在易陷入局部最优、收敛速度慢的缺点,因此采用群体智能优化算法中的粒子群算法对BP神经网络的权值和阈值进行优化。粒子群算法优化的基本原理[11-12]是:在一个D维的搜索空间中,有n个粒子会搜索最优解,在每次迭代过程中,粒子会通过粒子个体极值和种群全局极值更新自身的速度和位置,更新公式为: (22) (23) 式中:w为惯性权重;Vid为第i个粒子的第d个速度分量;Xid为粒子位置;Pid为个体极值;Pgd为全局极值;k为当前迭代次数;C1和C2为学习因子;r1和r2为[0,1]范围内的随机数。 PSO-BP神经网络算法具有收敛速度快、精度高且不受模型结构影响的优点,兼顾了网络初始阈值和权值的优化,具有更小的训练误差和检验误差,提高了网络的学习和泛化能力[13-14]。PSO-BP流程图如图1所示。 图1 PSO-BP流程图 盾构密封舱采用5个压力传感器实时采集密封舱土压,分别安装在承压板上侧、左上、右上、左下和右下位置,如图2所示,5点土压值分别为P1、P2、P3、P4、P5。以密封舱上点P1点压力传感器采集的数据为例进行仿真实验。 图2 密封舱压力传感器分布位置 因为需要优化螺旋输送机转速,所以将下一时刻的螺旋输送机转速也作为模型的输入变量,以推进速度V(t)、总推进力F(t)、刀盘扭矩M(t)、当前时刻螺旋输送机转速N(t)、下一时刻螺旋输送机转速N(t+1)和当前时刻密封舱土压值Pe(t)作为模型的输入变量,X=(V(t),F(t),M(t),N(t),N(t+1),Pe(t)),以下一时刻密封舱土压Y=Pe(t+1)作为模型的输出,因此盾构机密封舱土压预测模型的形式为: Pe(t+1)=f(V(t),F(t),M(t),N(t),N(t+1), Pe(t)) 使用的BP神经网络结构如图3所示。 图3 预测模型BP神经网络结构 为验证模型的有效性和可行性,采集武汉某地下隧道施工现场设备400组s数据,隧道埋深在20~25 m之间。采用德国海瑞克公司的直径为6.28 m的土压平衡式盾构机,通过PLC和上位机监控系统[15]实时采集盾构机上的各种数据并存储到数据库中,参数主要包括密封舱5点土压、总推进力、刀盘扭矩、掘进速度、螺旋输送机转速、油缸压力和行程等。 选择施工现场传感器采集的200组数据作为训练集进行训练,另外200组数据作为验证。在进行仿真实验之前需要对输入数据进行归一化处理: (24) 本次仿真采用均方误差函数MSE来评价该预测模型的性能和预测效果。MSE的值越小,则证明模型的预测性能越好,其计算公式为: (25) BP神经网络结构为6-15-1三层结构,网络隐含层传递函数采用S型的对数函数tansig,输出层采用线性函数purelin,训练函数采用trainlm,学习函数采用learngdm,网络的训练次数为2 000次,学习的效率为0.05,网络训练目标误差为0.000 1。 设定粒子种群规模为30,最大允许迭代次数为300,加速度因子C1=C2=1.494 45,对初始粒子的速度和位置赋随机值,规定精度为0.05。参数初始化完成之后对粒子群算法进行编程模拟。 图4给出了在相同的数据条件下,PSO-BP神经网络与传统BP神经网络密封舱土压预测值与实际土压值的对比。图5给出了PSO-BP与传统BP神经网络密封舱土压预测误差曲线对比。可以明显看出,PSO-BP算法的预测精度明显优于BP神经网络。 图4 PSO-BP和BP神经网络土压仿真结果 通过以上的对比分析可以很明显地看出基于粒子群算法优化的BP神经网络对密封舱土压的预测精度更高,很好地修正了BP神经网络土压预测的误差,表明粒子群算法对BP神经网络的初始权值和阈值具有很好的优化效果。 在盾构掘进的过程中,密封舱的土压平衡控制主要是通过调整螺旋输送机转速实现[16]。结合上文密封舱土压预测模型,以密封舱5点土压预测值与各点土压设定值的偏差最小为目标函数,采用粒子群算法对螺旋输送机转速进行优化,得到最优的螺旋输送机转速并将其反馈到液压驱动系统,从而保证密封舱的土压平衡控制,即找到N(t+1)使得: 图5 神经网络误差曲线 图7 5点土压优化前后对比 (26) Nmin≤N(t+1)≤Nmax (27) 图6 PSO优化螺旋输送机转速 通过图7可以看出,经过PSO优化螺旋输送机转速之后的密封舱各点土压波动小,而且与设定值误差较小,说明此方法能够很好地对密封舱进行土压平衡控制,维持刀盘开挖面的稳定性,保证施工的安全。采用粒子群算法对控制模型进行优化的过程所需时间不到50 s,为盾构控制参数的调整提供了充足的时间。采用排土控制模式对密封舱土压进行调节,降低了系统的耦合性,使盾构系统更加稳定高效,说明了此控制策略在实际工程中的可行性。 本文提出了采用掘进机理与PSO-BP神经网络算法相结合的方法建立盾构推进过程中的土压预测模型,在此土压预测模型的基础之上提出了采用PSO粒子群智能算法对螺旋输送机转速进行实时优化的方法,并进行了仿真验证分析。实验结果表明,粒子群智能算法能够很好地优化神经网络的连接权值和阈值,模型控制精度和速度得到了提高。采用PSO算法对控制参数进行优化调整,使下一时刻的密封舱土压能够很好地跟随土压设定值,有效地保证密封舱土压平衡,避免因密封舱压力失衡而造成地表的坍塌或隆起。 参考文献 [1] MASHIMO H. State of the road tunnel safety technology in Japan[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2002, 17(2):145-152. [2] REILLY J J. The management process for complex underground and tunneling projects[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2000, 15(1):31-44. [3] SHIN H S, KWON Y C, JUNG Y S, et al. Methodology for quantitative hazard assessment for tunnel collapses based on case histories in Korea[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(6):1072-1087. [4] 刘宣宇, 邵诚. 盾构机自动控制技术现状与展望[J]. 机械工程学报, 2010, 46(20):152-160. [5] 朱合华, 徐前卫, 郑七振,等. 软土地层土压平衡盾构施工参数的模型试验研究[J]. 土木工程学报, 2007, 40(9):87-94. [6] YEH I C. Application of neural networks to automatic soil pressure balance control for shield tunneling [J]. Automation in Construction, 1997, 5(5):421-426. [7] 施虎, 龚国芳, 杨华勇,等. 盾构掘进土压平衡控制模型[J]. 煤炭学报, 2008, 33(3):343-346. [8] 王洪新, 傅德明. 土压平衡盾构掘进的数学物理模型及各参数间关系研究[J]. 土木工程学报, 2006, 39(9):86-90. [9] 管会生. 土压平衡盾构机关键参数与力学行为的计算模型研究[D]. 成都:西南交通大学, 2007. [10] 王洪新. 土压平衡盾构刀盘扭矩计算及其与盾构施工参数关系研究[J]. 土木工程学报, 2009,42(9):109-113. [11] SUWANSAWAT S, EINSTEIN H H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling[J]. Tunnelling & Underground Space Technology, 2006, 21(2):133-150. [12] 洪亮, 李瑞娟. 基于粒子群算法优化BP神经网络的色彩空间转换[J]. 包装工程, 2014,35(9):105-109. [13] 张捍东, 陶刘送. 粒子群优化BP算法在液压系统故障诊断中应用[J]. 系统仿真学报, 2016,28(5):1186-1190. [14] 郭亚强, 王鹏, 白艳萍. 基于PSO-BP神经网络的矢量水听器的DOA估计[J]. 传感技术学报, 2016, 29(8):1229-1233. [15] 郑朝虹. 地铁盾构机传感器应用技术[J]. 地下工程与隧道, 2009(3):17-18. [16] SHAO C, LAN D. Optimal control of an earth pressure balance shield with tunnel face stability[J]. Automation in Construction, 2014, 46(10):22-29.1.3 刀盘扭矩和密封舱压力的关系
2 基于PSO-BP的密封舱土压预测模型建立
2.1 基于粒子群优化BP神经网络的算法
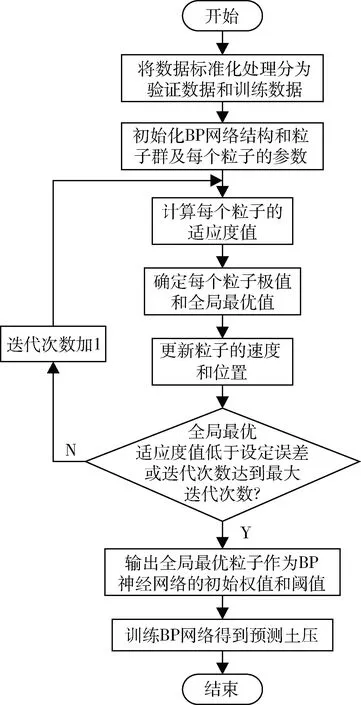
2.2 预测模型的建立
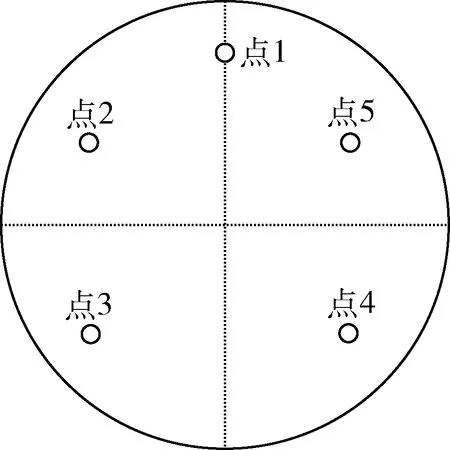
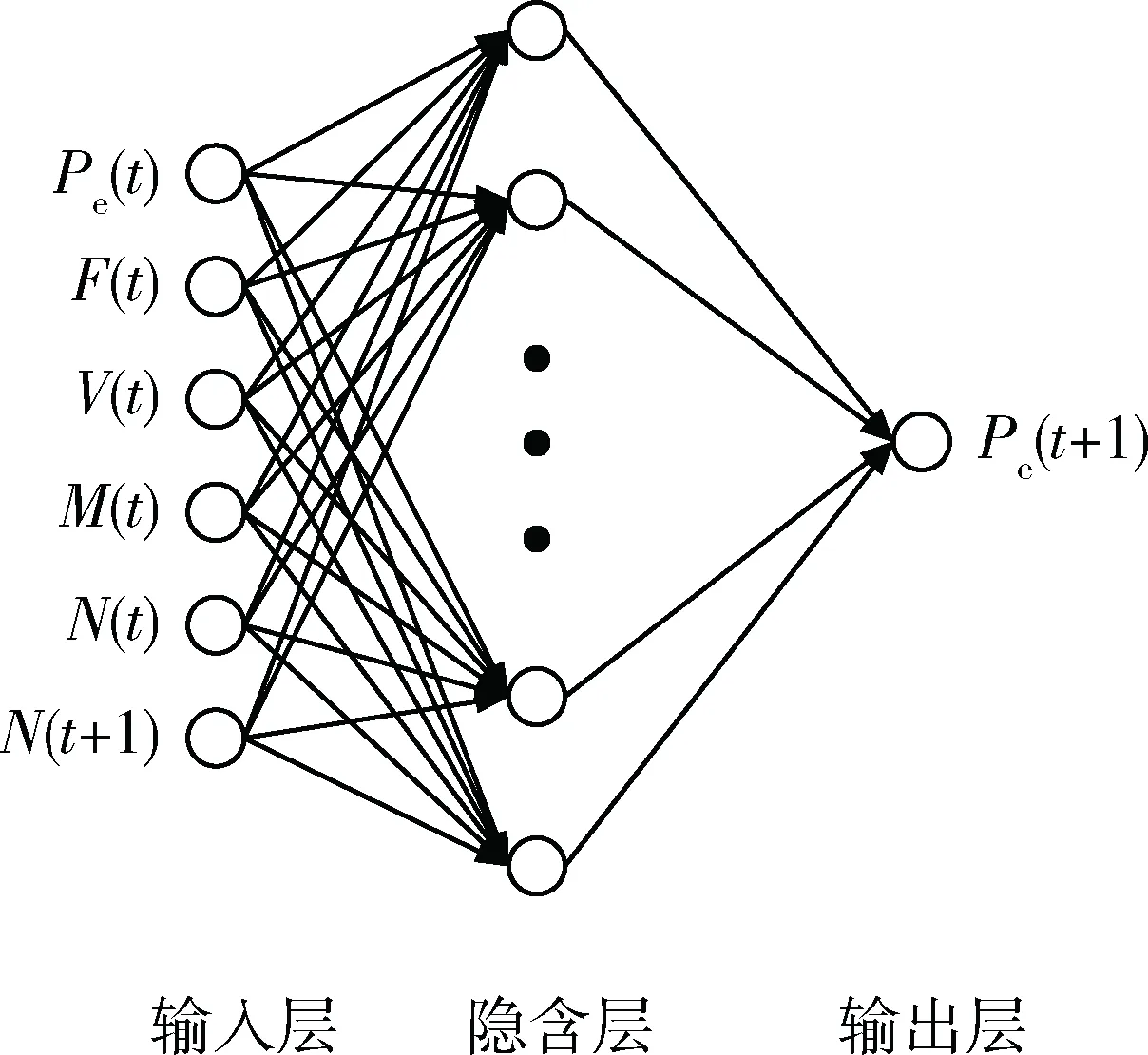
3 仿真实验及分析
3.1 工程概况
3.2 PSO-BP神经网络土压预测模型仿真
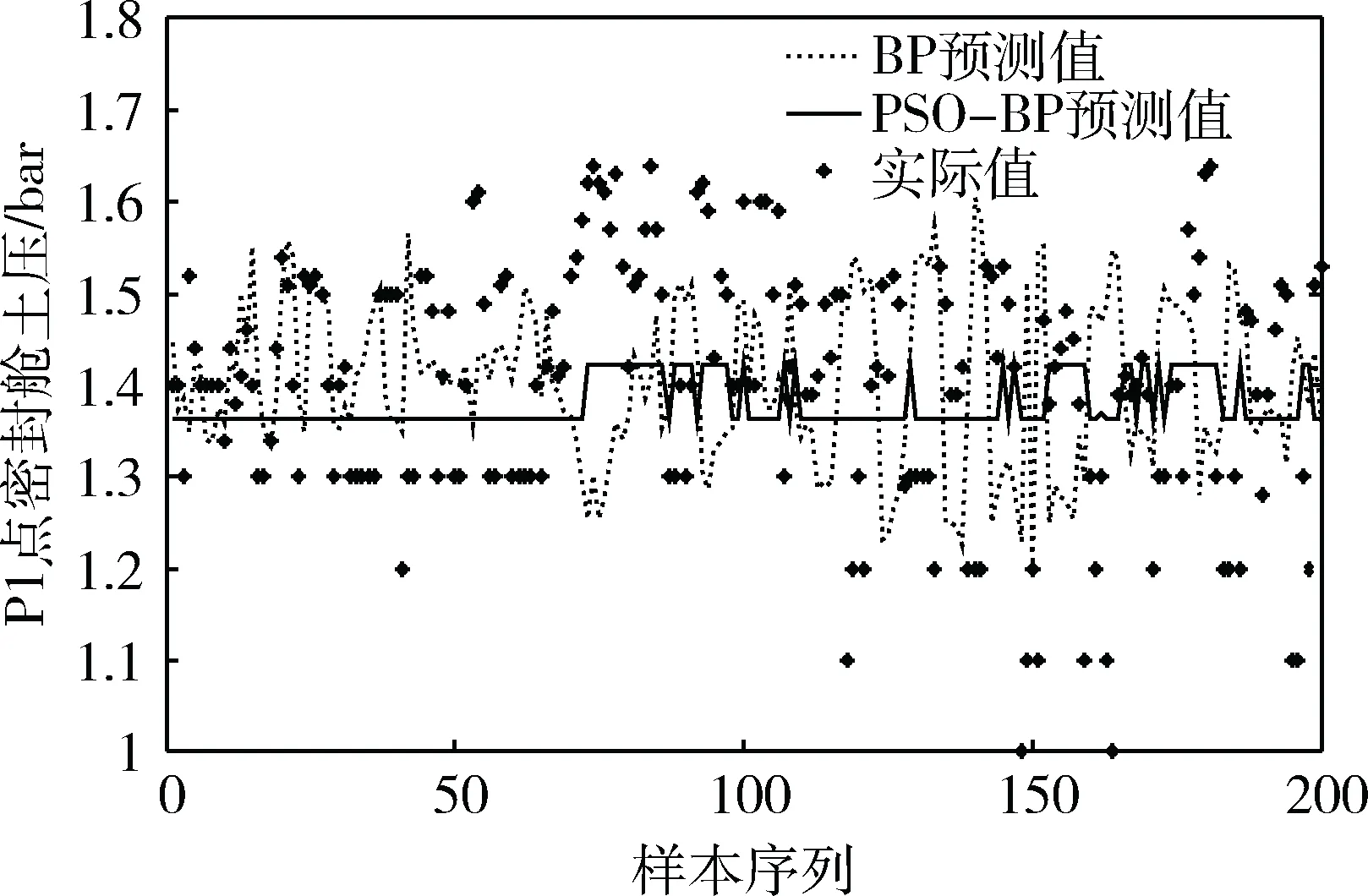
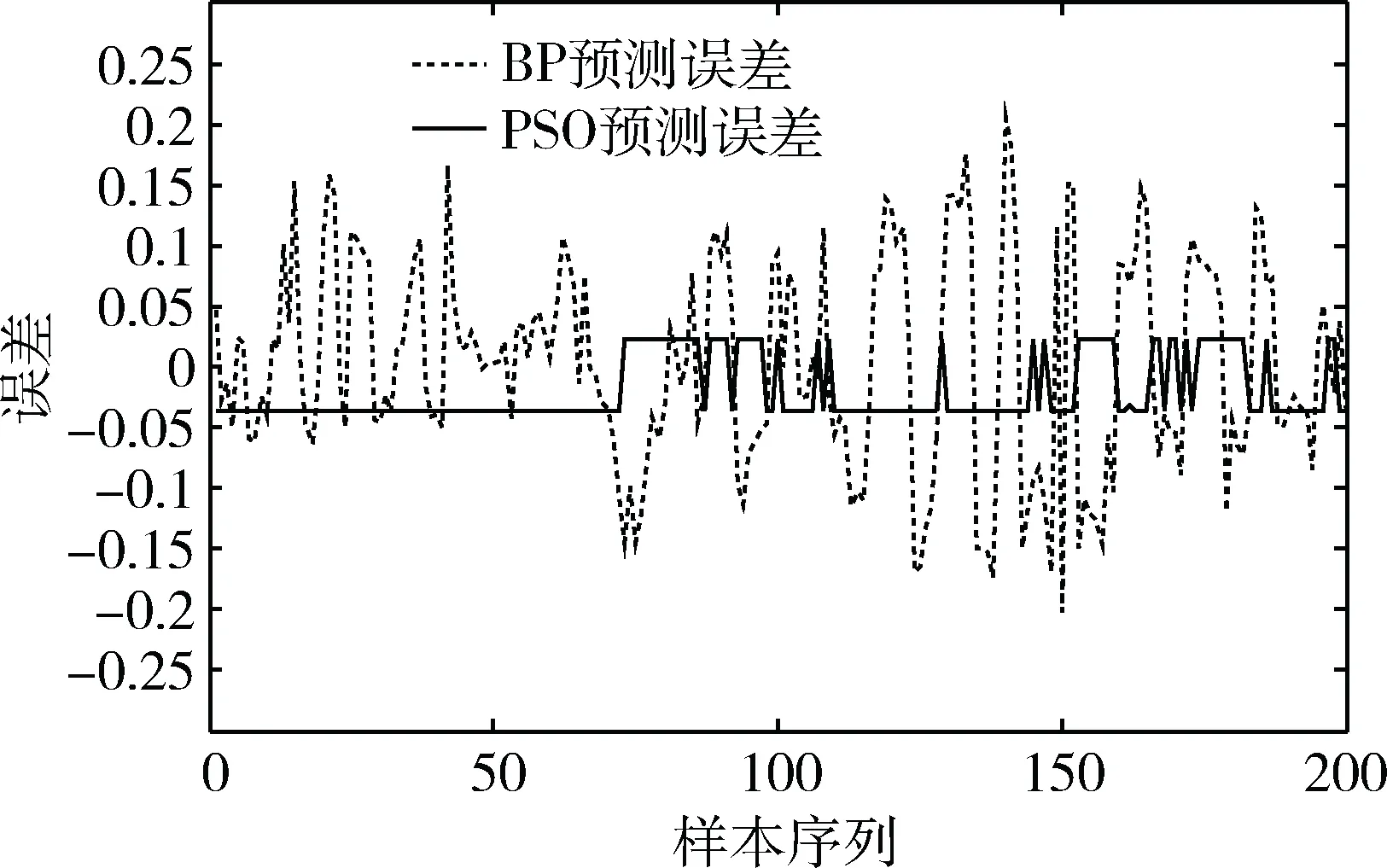
4 基于粒子群算法的螺旋输送机转速优化
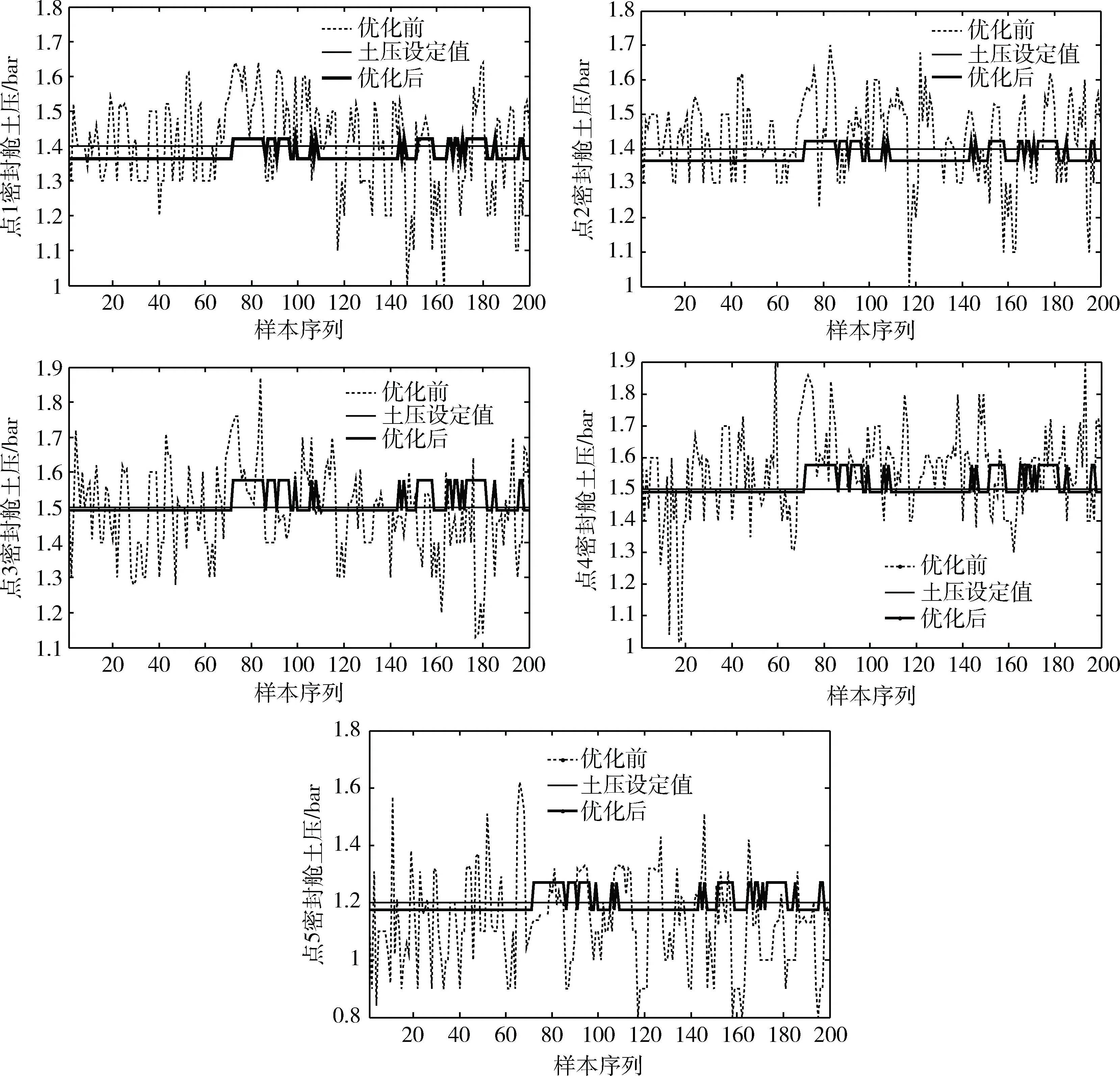
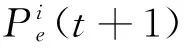
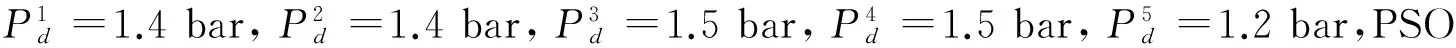
5 结论
