波束形成算法研究与改进

刘 权，周渊平，徐 磊，黄思远

(四川大学 电子信息学院，四川 成都 610065)

0 引言

智能天线系统是由阵列天线、模数转换、自适应波束形成等几部分构成的。自适应处理系统可以根据信号的空时域特性和高效的自适应准则，采用有效的算法，产生最优化的权值，进而实现信号的最佳接收状态。波束形成算法是智能天线技术的核心内容之一[1]，算法收敛速度的快慢、计算复杂度、应用效果等因素都直接影响智能天线系统的性能。采用合适的波束形成算法成为研究重点。

1 算法分析

1.1 LMS算法

对于有M个阵元的均匀直线阵列的输入信号为S(n)=[s0(n),s1(n),…,sM-1(n)]T，通过各个阵列元通道的加权后，合成的输出信号表示为：

y(n)=WTS(n)

(1)

式中：

W=[w0,w1,…,wM-1]T

阵列输出信号的均方为:

=E[(WTS(n)SH(n)W*)*]

=WHE[S*(n)ST(n)]W=WHRW

(2)

其中R=E[S*(n)ST(n)]

误差信号定义为：

e(n)=d(n)-y(n)

(3)

式中d(n)为期望得到的信号。

期望信号与阵列输出信号的差值的均方误差ξ为：

(4)

式中：R=E[x*(n)x(n)],r=E[x*(n)d(n)]

均方误差ξ对加权向量W的梯度表示为：

(5)

当梯度为零时，均方误差信号的函数取得极小值[2]，由此可得到：

Wopt=R-1r

(6)

为了减少算法的复杂度，避免矩阵的求逆计算，一般采用最陡下降法的LMS算法逐次迭代加权值的向量。在最陡下降法中[3]，可以设置一个W的初始值W(0)，用均方误差减小的方向来不断地调整W，可以找到一个较优化的Wopt，采用的递推公式为：

W(n+1)=W(n)-mNwx

=W(n)-2m[RW(n)-r]

(7)

其中，m为步长，是一个常数。在该梯度算法中需要R与r的精确数值，所以要求输入信号和误差信号必须要稳定，而且要求二阶统计特性是已知的。但是在实际的应用场景中，满足这样的要求比较困难，于是采用估计值代替精确值。可以采用输入信号和误差信号的瞬时值来估计互相关矩阵与自相关矩阵，于是R=x*x,r=x*d，因此，式(7)可以改写为式(8)：

W(n+1)=W(n)+2me(n)x*(n)

(8)

1.2 GSC算法

广义旁瓣信号相消器由主支路和辅助支路两部分组成，并且要求期望信号只能从主支路加权值通过，辅助支路中只含有噪声分量和干扰信号，两条支路不断地自适应进行差值得到理想的输出信号[4]，算法的具体描述如下：

输出信号的功率为：

(9)

其中，W=WC-BHWa为GSC整体权值，WC为主支路权值，Wa为辅助支路的自适应权值，B为M×(M-1)维的阻塞矩阵，BHC=0，B的作用就是阻塞掉理想的期望信号，组成B的列向量是位于构造约束空间的正交互补空间中的向量[5]，R=E[S*(n)ST(n)]。

整体权值也可以表示为：

WC-BHWa=R-1CH(CR-1CH)-1c

(10)

其中，C是信号方向矢量，c是一个常数。

主支路权值为：

WC=CH(CCH)-1c

(11)

阻塞矩阵满足的约束条件为：

BCH=0

(12)

辅助支路权值为：

Wa=(BRBH)-1BRWc

(13)

由此可知，广义旁瓣信号相消器实现了能够消除干扰和噪声，输出理想的信号[6]。

1.3 MMSE算法

该波束形成算法是求取一个最优的权值，能够使阵列天线输出与参考信号的差异最小，也就是[7-8]:

minE[|WTr(t)-d(t)|2]

(14)

式中，W为权值，r(t)是输入信号,d(t)是参考信号。

扩展式(14)，得:

E[|WTr(t)-d(t)|2]=WHE[r*(t)r(t)T]W-WHE[d(t)r*(t)]-E[d*(t)r(t)T]W+E[d*(t)d(t)]=J(W,W*)

(15)

将式(15)的梯度向量设为0:

(16)

可得到最优解为：

Wopt=R-1P

(17)

其中：

R=E[r*(t)r(t)T]

(18)

P=E[r*(t)d(t)]

(19)

1.4 三种算法仿真实验结果

仿真环境如下：阵元个数为12，信噪比SNR均为10 dB，快拍数1 000，信干噪比SINR=-2 dB，仿真信道满足瑞利信道的模型构造，仿真包含1个理想信号，3个独立的干扰。

三种算法的波束图比较如图1所示，可以看出，MMSE的分辨率效果最好，同时在干扰抑制效果上，MMSE最好，LMS和GSC次之。MMSE动态权值矢量能够自适应地在期望方向形成峰值并在干扰方向形成零陷，具有抑制干扰的能力和高分辨率的特点。但是MMSE算法也有一些缺点，即天线数量较多时，计算量太大，对硬件的要求高，无法跟踪信道参数，会受到干扰信号的时延影响。

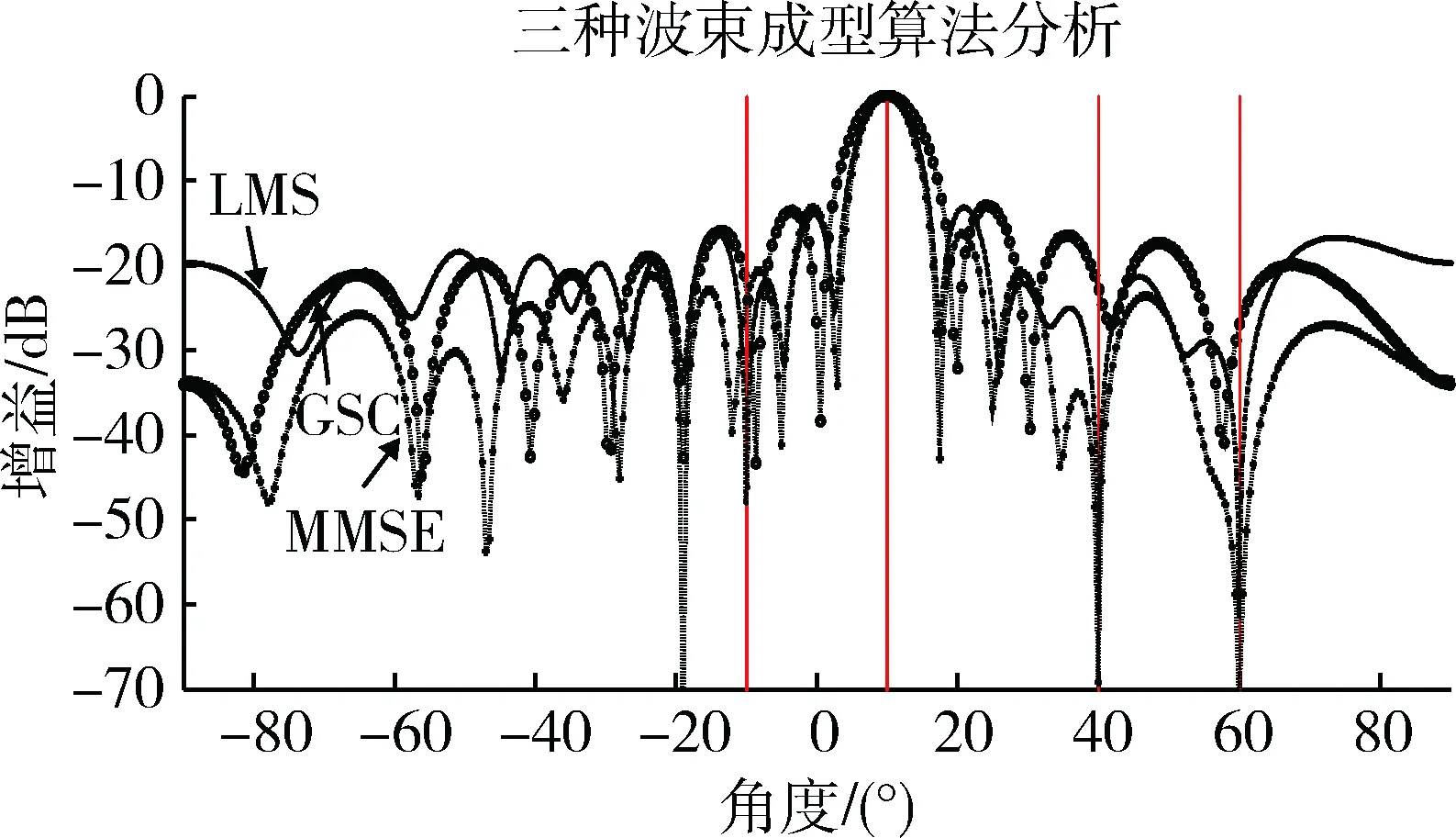
图1 LMS、GSC、MMSE三种算法的空间谱

2 MMSE算法的改进

传统的MMSE算法是通过公式(17)来确定最优权值的，这样增加了算法的复杂度和计算量。特别是在大规模天线的情况下，这样对硬件的要求太高，因此，MMSE算法的改进在于实现单根天线单权值的调整，采用自适应的算法完成天线的最优权值搜索。

传统MMSE的约束方程为：

J=E[|WHX(n)-d(n)|2]

(20)

将传统方程中WHX(n)进行转化：

(21)

其中：

(22)

Xk(n)表示第k个接收天线的接收信号。

将式(22)代入式(21)中得到：

|d(n)|2

(23)

将式(23)求导，得：

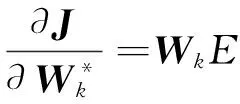
(24)

因此可以得到：

(25)

其中:

λ2=E[|xk(n)|2]

(26)

仿真环境如下：阵元个数为16，信噪比SNR为10.2 dB，快拍数为1 000，信干噪比SINR=-1.5 dB,天线间距为1/2波长，仿真信道满足瑞利信道的模型构造，仿真包含一个理想信号(角度0°)和理想信号的多径(角度50°)，以及两个独立的干扰(角度为-20°和10°)。

仿真结果如图2～图4。图2中，单权值MMSE算法的波束图与传统MMSE的波束图相比，前者对多种干扰的抑制作用更加明显，对理想信号的多径都具有较好效果。

图3中，两者的初始信噪比SNR=18.5 dB；经过智能天线的算法处理后，普通MMSE算法的信干噪比SINR1=25.3 dB；单权值调整MMSE算法的信干噪比SINR2=25.6 dB，经过逐个天线调整的最优权值对干扰的抑制作用稍高于普通的MMSE算法。

图4中，随着单根天线的权值迭代次数的增加，误码率也会降低，经过一段时间的迭代，权值会达到一个较优的状态，使误码率保持在低值。

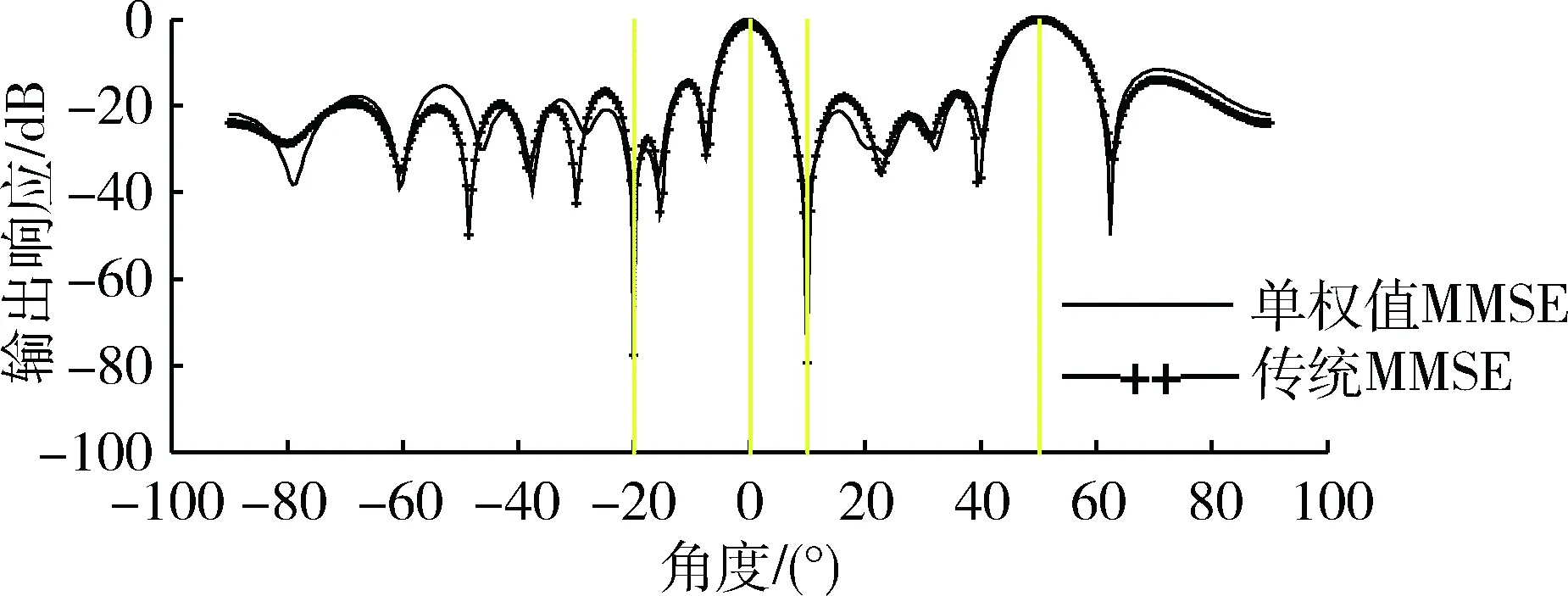
图2 传统MMSE和单权值调整MMSE的波束图

图3 改进MMSE算法与传统MMSE的收敛图

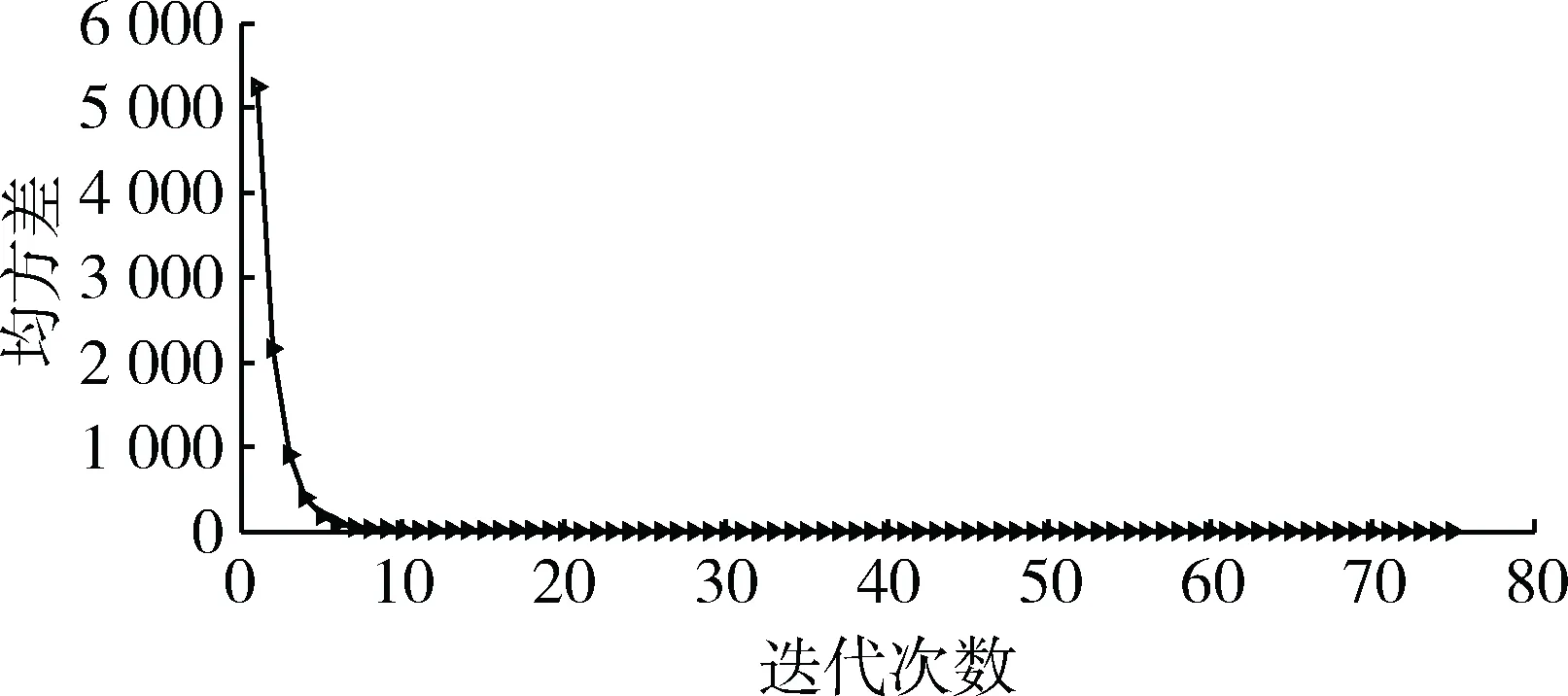
图4 改进MMSE算法误差趋势图

3 结论

本文分析了LMS、GSC、MMSE三种算法的原理，实际上阵元个数、天线间距、初始信噪比、快拍数等因素都会影响波束形成算法的效果，在相同条件的情况下，比较了三种算法的性能。传统MMSE算法能够使主瓣对准理想信号的方向，对干扰方向进行零陷，从而提高阵列输出的信噪比，具有较好的抑制干扰的作用。GSC 算法与阻塞矩阵的个数有较大的关系，阻塞矩阵与天线的个数有关，矩阵求逆运算复杂度较高。LMS算法在稳定且信号统计未知的情况下，通过递归迭代的算法求出理想权值，但是没有利用之前循环的阵列的样本信息，导致估计的梯度协方差偏大，更新的权向量不能很好地抑制干扰。尽管传统MMSE算法在抑制干扰上有较好效果，但是矩阵的求逆导致复杂度较高，在实际应用中对硬件要求高。单根天线逐步调整的MMSE算法避免了这种情况，同时提高了信噪比，抑制干扰的能力有一定提升，但是单权值MMSE和传统MMSE都没有解决干扰信号时延造成波峰混叠的问题，在今后的研究中，将进一步提高该算法的性能。

参考文献

[1] 王永良，丁前军，李荣锋，等.自适应阵列处理[M]. 北京：清华大学出版社，2009.

[2] 张骅，郭卫展. LMS自适应波束形成[C]. 北京：第十届全国雷达学术年会，2009.

[3] 李海波.基于LMS算法的自适应波束形成的性能研究[D].重庆：重庆大学，2010.

[4] GROSS F. Smart antennas for wireless communications: with MATLAB[M]. 北京：电子工业出版社，2009.

[5] 李炜 孙超.一种用于波束形成的改进LMS算法分析[D].西安：西北工业大学，1994.

[6] 金荣洪，耿军平，范瑜, 等.无线通信中的智能天线[M]. 北京：北京邮电大学出版社，2006.

[7] 李洪涛.自适应数字波束形成关键技术研究[D].南京：南京理工大学，2010.

[8] 康锐坚.用于智能天线技术中的MMSE波束成形器[D].广州：中山大学，2005.