免疫粒子群优化的DV-Hop定位算法

吴珍珍，方旺盛

(江西理工大学 信息工程学院，江西 赣州 341000)

0 引言

WSN节点定位技术是WSN应用于目标监测、目标识别和目标跟踪的支撑技术，其算法可分为基于非测距(Range- free)的算法和基于测距(Range-based)的算法[1]，其中非测距DV-Hop算法因具有成本低、能耗小、算法实现简单等特点而被广泛应用，但该算法也存在定位误差较大的不足。

为了提高DV-Hop算法的定位精度，国内学者对此引入群体智能算法进行优化。文献[2]提出了一种改进的粒子群优化DV-Hop算法，从惯性权重的计算、粒子速度的更新等方面对粒子群算法进行改进，提高算法的搜索速度，再采用改进粒子群算法优化节点的定位结果，降低了定位误差。文献[3]利用免疫系统里的调节机制来提高种群的多样性，避免了过早陷入局部最优解，优化的DV-Hop算法提高了定位效果，但该算法未考虑粒子群算法的收敛速度问题。文献[4]使用遗传机制中的前摄估计缩小粒子搜索范围，再用改进粒子群算法以代替最小二乘法优化了DV-Hop算法定位精度。本文根据免疫粒子群算法的特点，利用该算法来优化DV-Hop定位算法求解未知节点的坐标。

1 DV-Hop定位算法

1.1 基本原理

DV-Hop(Distance Vector-Hop)是一种非测距定位算法。该算法依赖于节点间的互相通信，具体定位算法由3个阶段组成[5]：

第一阶段：信标节点通过全网泛洪广播数据包，所有节点可以记录下到每个信标节点的最小跳数。

第二阶段：估算从未知节点到信标节点的跳距。

第三阶段：利用三边测量法或最小二乘法等计算未知节点坐标[6]。

1.2 定位误差的分析

从DV-Hop的工作原理可知，其产生定位误差的主要原因有跳数、平均每跳距离、定位的计算方法等。

(1)跳数信息不合理

WSN在定位时通过使用跳数信息计算节点之间的距离，而无线传感器网络中的节点大都是随机分布，未知节点与锚节点之间并非都是直线距离，所以节点之间存在弯曲路径，将会导致较大误差。

(2)平均跳距的估计值不准确

在DV-Hop定位算法中，节点间的距离计算是采用同一个平均距离的估计值乘以对应的跳数来计算的，存在一定的定位误差。

(3)定位的计算方法累计误差

计算未知节点的坐标时经常采用三边测量和极大似然估计法。三边测量方法虽然降低了计算量，但其受限于第二阶段的跳距估计。而在最大似然估计法求解过程中需要较多的浮点预算，计算开销带来的功耗不容忽视。

2 免疫粒子群优化的DV-Hop定位算法

鉴于上述误差分析，针对经典DV-Hop定位算法在计算未知点坐标上存在较大误差，本文提出了一种免疫粒子群优化的DV-Hop定位算法。

2.1 粒子群算法进化模型

粒子群优化(Particle Swarm Optimization,PSO)算法是1995年由Kennedy和Eberhart提出的一种新型的随机群体智能的进化算法[7]。其原理为：在D维空间里有很多“粒子”，这些“粒子”通过“位置+速度”模型来更新自身的位置与速度，每个粒子不断地搜索迭代，向最优值位置不断地靠近[8]。该算法存在以下缺点：(1)容易陷入局部极小值，导致得不到全局最优解；(2)没有充分的优选机制，收敛速度较慢。本文为了提高粒子群算法的全局搜索能力，借鉴免疫算法的思想改进PSO算法，当PSO算法陷入局部最优解时，通过免疫抗体的选择、促进和抑制机制产生新的粒子空间，使该算法跳出局部最优值，避免“早熟”；另外生成的免疫记忆细胞可以加快收敛速度，确保快速收敛于全局最优解。

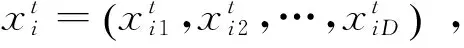
(1)

(2)

式中，c1表示个体学习因子，c2表示全局学习因子，而r1和r2为(0,1)上均匀分布的随机数；ω为惯性权重，表示粒子运动的趋势，对全局搜索和局部搜索起到平衡作用[9]。该系数按照公式(3)进行更新。

(3)

2.2 免疫机制

免疫机制源于生物免疫系统，其具体思路为将待优化适应度函数最优解看作入侵生命体的抗原，而免疫系统产生的抗体即为候选解，将个体最优解以免疫记忆形式保存于记忆细胞，提高收敛速度；根据免疫调节机制，选择具有亲和度高且浓度低的抗体进化，而亲和度低浓度高的抗体加以抑制[10]；通过抗原抗体相互促进抑制来维持抗体的多样性，克服了粒子群算法在实际工程优化计算中的早熟收敛现象，提高了算法的全局搜索效率。

(1)亲和度

亲和度[11]用来衡量抗原与抗体间的匹配程度，即所求的解与最优解的接近程度，记为aff，计算公式如下：

(4)

其中，f(xi)为xi的适应度函数，η为(0,1)上的常数。由上式可以看出，当f(xi)越小时，抗体的亲和度越大，所求的解与最优解就越逼近。

(2)浓度

浓度表示抗体与其相似的粒子在群体中所占的比例，反映种群多样性的程度。假设存在i个抗体x1,x2…,xi，每个抗体按照亲和度从小到大排序并分成m个等份区间，其中m=1,2,…，m。计算每个区间的抗体数，记为sum(m)，得到每个区间的浓度为sum(m)/m，将每个抗体的浓度定义为该抗体所在区间的浓度，记为D，则有：

(5)

由上式可知，同一个区间上的抗体浓度是相同的，这使得抗体浓度越高反而越受到抑制，而抗体浓度越低反而得到进化的机会。

(3)选择概率

选择概率是指抗体在进化过程中得到促进发展的概率。假设基于亲和度的选择概率为Pa，而基于浓度的选择概率为Pd，计算公式如下：

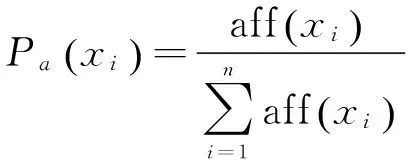
(6)

(7)

则抗体被选中的选择概率P为：

P(xi)=αPa(xi)+(1-α)Pd(xi)

0<α,Pa,Pd<1

(8)

式中i=1,2,…,n；α为免疫协调因子，用来协调概率Pd和Pa的权重。从式(8)可以得知，浓度越高、亲和力越低的抗体被选择的概率越小；而浓度越低、亲和力越高的抗体获得进化的概率越大。这样既提高了抗体的亲和度，又保证了粒子的多样性，从而得到较大的解空间。

(4)适应度函数

适应度函数即目标函数，用来评价给出的候选解(抗体)的优劣。计算公式如下：

(9)

其中，M(M≥3)为未知节点接收到的信标节点的个数；(x,y)和(xi,yi)分别表示粒子位置和第i个信标节点的坐标；di为未知节点到信标节点i的欧式距离。适应度函数f(i)的极小值点则为最优的定位坐标。

3 免疫粒子群优化的DV-Hop定位算法步骤

本文算法优化的DV-Hop算法步骤如下：

(1)初始化网络区域、节点总数、粒子群相关参数。

(2)根据经典DV-Hop算法的第一和第二阶段获得每个信标节点和未知节点的最小跳数以及信标节点i的平均跳距，计算跳段距离。

(3)初始化粒子群。初始化粒子位置X、粒子速度V、历史局部最优位置pbesti=Xi，计算种群的适应度函数值，取该值的最小值为粒子群的全局最优位置gbesti的初始值。

(4)免疫记忆。将粒子按亲和度从小到大排序,取亲和度较大的粒子存入免疫记忆细胞中。

(5)利用式(1)、式(2)分别更新粒子的飞行速度和位置，产生n个新的抗体，然后从免疫记忆细胞中抽取q个抗体，组成规模为n+q的抗体群。

(6)免疫替换，丢弃位置较差的粒子(抗体)。利用式(4)～(8)计算抗体的选择概率，依据选择概率从n+q个抗体中选择出n个抗体，则选择概率大的抗体将被选中，组成新的抗体群，从而实现抗体的多样性，避免出现“早熟”。

(7)根据式(9)计算抗体的适应度大小，比较所有粒子当前的适应度值F(Xi)和局部最优位置适应度值F(pbesti)，若F(pbesti)>F(Xi)，则更新pbest值;再用更新后局部最优适应函数值F(pbesti)与全局最优位置的适应函数F(gbesti)比较，若F(gbesti)>F(pbesti)，则更新gbest值。

(8)若满足终止条件，则输出全局最优解gbesti，适应度函数F(gbesti)的极小值点即为未知节点的最终定位坐标。否则返回步骤(4)。

4 实验与仿真

4.1 实验环境和参数设置

为验证本文算法的有效性，本文基于Windows 10操作系统的MATLAB 2014平台进行仿真实验。本文试验场景设置为100 m×100 m的二维正方形区域，假设所有WSN网络节点的通信半径都为R。

免疫粒子群算法的初始化参数如表1所示。

表1 仿真参数

4.2 仿真分析

(1)信标节点比例对定位精度的影响

假设通信半径为30 m、节点总数为100，图1给出信标节点比例对定位精度的影响关系图。从图中可以看出，3种定位算法的平均定位误差都随着信标节点的比例增加而减小。当信标节点比例相同时，本文算法的平均定位误差与DV-Hop以及PSO-DV-Hop定位算法比较降低了15.03%、4.86%。另外，本文算法平均定位误差曲线更平滑，表明其稳定性更好。

图1 信标节点比例与定位误差关系图

(2)通信半径对定位精度的影响

假设节点总数为100时，信标节点比例为10%，改变通信半径进行仿真，结果如图2所示。从图中可以看出，在通信半径小于30 m时，3种定位算法的平均定位误差都随着通信半径的增大而明显减小，这是因为通信半径的增大提高了未知节点与信标节点的连通性，从而可以获得更大范围的信息交换来提高定位精度。但在通信半径大于30 m时，平均定位误差缓慢减小，趋于平滑，因此通信半径并不是越大越好，通信半径的增大也将提高通信开销。另外，从3种算法对比可以看出，本文算法的定位误差与经典DV-Hop、PSO-DV-Hop定位算法相比，定位精度提高了13.27%、8.27%。

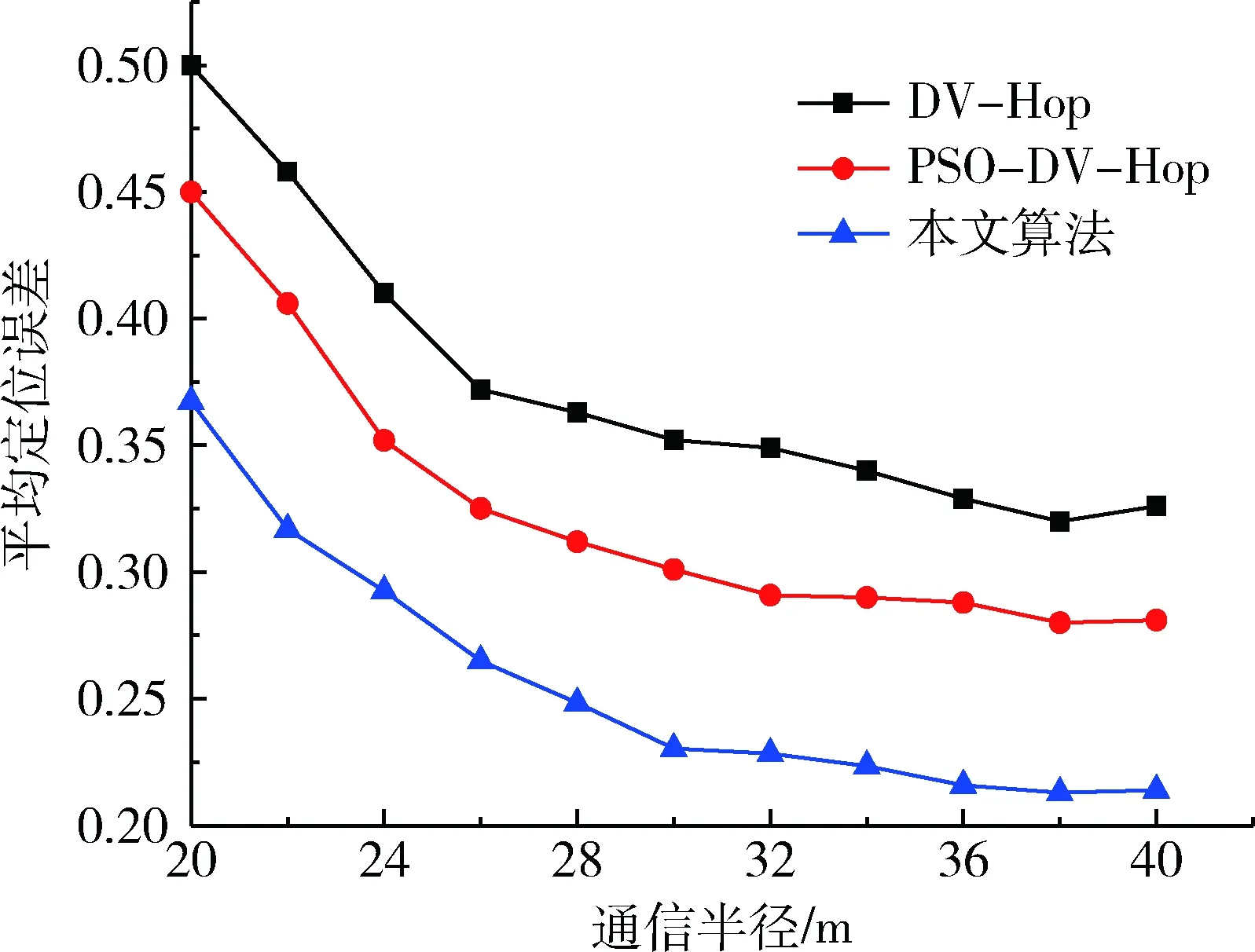
图2 通信半径与定位误差关系图

(3)节点总数对定位精度的影响

假设网络节点的通信半径为30 m时，信标节点比例为10%，节点总数变化的仿真结果如图3所示。从图中可以看出，在通信半径和信标节点比例相同的情况下，节点的平均误差随着节点总数的增加而下降。随着节点总数的变化，平均定位算法的变化幅度相对较大，这也反映了该算法的可扩展性有待进一步提高。但是，本文算法定位精度明显优于传统的DV-Hop算法和PSO-DV-Hop算法，平均定位误差分别降低了10.85%、5.89%。

图3 节点总数与定位误差关系图

5 结论

本文阐述了典型DV-Hop定位算法的基本原理，分析了DV-Hop定位算法的误差来源，并结合免疫粒子群优化算法的特点，提出了一种免疫粒子群算法优化的DV-Hop定位算法。在免疫粒子群算法中，通过调节机制使各适应度的粒子维持一定浓度，保证群体的多样性，克服粒子早熟，使得粒子快速收敛于全局最优点，优化待测节点位置坐标。该算法在无需增加额外硬件设备的情况下，有效降低了定位误差。但免疫粒子群算法的引入增加了算法复杂度，这将是下一步研究的重点。

参考文献

[1] 钱志鸿, 孙大洋. 无线网络定位综述[J]. 计算机学报, 2016, 39(6): 1237-1256.

[2] 于泉, 孙顺远, 徐保国, 等. 基于改进粒子群算法的无线传感器网络节点定位[J].计算机应用, 2015, 35(6): 1519-1522.

[3] FEI J.Optimization of immune particleswarm algorithmand application on wireless sensornetworks[J]. Computer Modeling & New Technologies,2014,18(11):1443-15448.

[4] 高美凤, 李凤超. 遗传粒子群优化的 DV-Hop 定位算法[J]. 传感技术学报, 2017, 30(7): 1083-1088.

[5] 王林,赵锦.一种基于误差修正的改进DV-Hop算法[J].计算机工程与应用,2014,50(24): 109-112.

[6] TAO Q, ZHANG L. Enhancement of DV-Hop by weightedhopdistance[C]//Advanced Information Management, Communicates, Electronic and Automation Control Conference(IMCEC),2016 IEEE, 2016:1577-1580.

[7] 邴晓瑛,徐保国.基于改进粒子群优化的WSN定位算法[J]. 电子设计工程,2015，23(22): 143-146.

[8] 张超, 李擎, 王伟乾, 等. 基于自适应搜索的免疫粒子群算法[J]. 工程科学学报, 2017, 39(1): 125-132.

[9] 张晓, 范虹, 张莉, 等. 融入免疫思想的改进型粒子群优化算法[J].陕西师范大学学报(自然科学版),2017,45(3): 17-23.

[10] Jiao Wei,Cheng Weimin,Zhang Mei,et al. A simpleand effective immune particle swarm optimization algorithm[C]// International Conference in Swarm Intelligence. Springer, Berlin,Heidelberg, 2012: 489-496.

[11] He Xingshi, Han Lin. A novel binary differential evolution algorithm based on artificial immune system [C]// Evolutionary Computation,IEEE,2007: 2267-2272.