简化复杂图形 提取核心要素

余中华

中考数学试卷中，常常可以看到这样的一些综合题，它们有着长长的题干，复杂的图形.大多数同学遇到这类题目往往心生畏惧，不知道如何下手.下面以南通市一道中考压轴题为例，评述我们该如何抓住关键点，提取题目中的核心要素.

已知抛物线y=x2-2mx+m2+m-1（m为常数）的顶点为P，直线l：y=x-1.

（1）求证：点P在直线l上.

（2）当m=-3时，抛物线与x轴交于A、B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上一点，∠PAQ=∠ACM（如图1），求点M的坐标.

（3）若以抛物线与直线l的两个交点及坐标原点为顶点的三角形为等腰三角形，请直接写出所有符合要求的m的值.

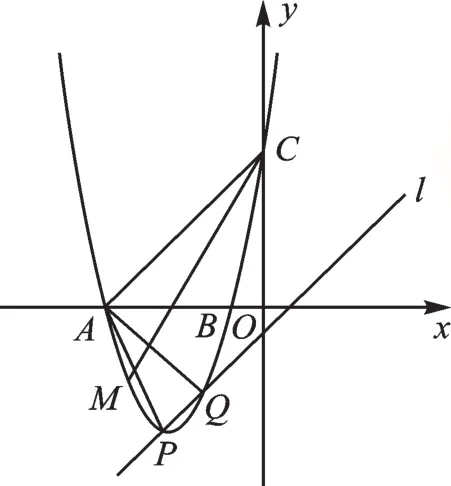
图1

第（1）小问，观察解析式可以发现x2-2mx+m2是一个完全平方式，因此这个解析式可以写成y=（x-m）2+m-1，很容易得到顶点P的坐标为（m，m-1）.接着证明P（m，m-1）在直线l上即可，此时就不用考虑其他条件和图形了，题目就简化成“求证P（m，m-1）在直线l上”.可将x=m代入y=x-1后看y的值是否是m-1.

其实P（m，m-1）不是一个点，随着m取不同的值，那么（m，m-1）就是不同的坐标，就代表一系列的点，这些点的横坐标x和纵坐标y总满足y=x-1，这也能说明点P不管坐标是什么，它始终在直线y=x-1上.

再看第（2）小问，当m=-3时，A、B、C、P、Q这些点的坐标都可以求出来.除了这些点，“∠PAQ=∠ACM”还涉及点M，M虽然是一个动点，但M始终是抛物线与直线CM的交点.抛物线的解析式已知，本题只要能求出直线CM的解析式，通过解方程组就可以求出点M的坐标.因此本题的关键步骤可以简化为：

如图2，已知P（-3，-4），A（-5，0），B（-1，0），C（0，5），Q（-2，-3），∠ACM=∠PAQ.求直线CM的解析式.

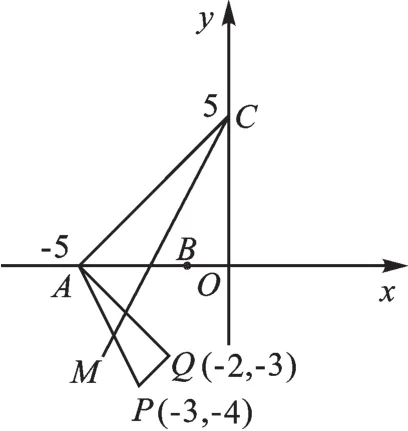
图2

很显然，要发挥点P、点Q的作用，需要将这两个点的横纵坐标都转化为线段的长，考虑过这两点作x轴的垂线，如图3，那么PE=4，AE=2，QF=3，AF=3，可见这个图中有两个等腰直角三角形△AFQ、△AOC，由∠ACM=∠PAQ就可以得到∠PAE=∠CGO（G为直线CM与x轴的交点），接着根据△PAE∽△CGO可求出G点坐标，从而求出CM的解析式，最后根据点M是CM和抛物线的交点，求出点M的坐标.

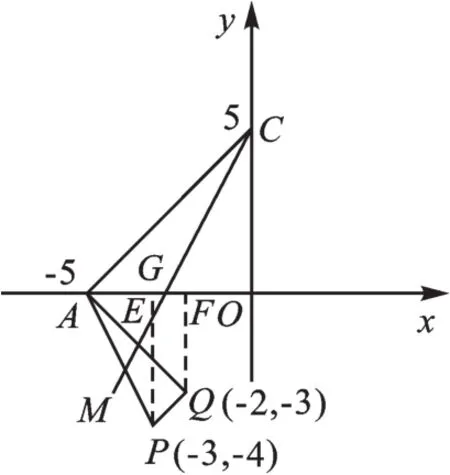
图3

第（3）小问讨论的是当△OPQ是等腰三角形时，求m的值.因此本题只需讨论O、P、Q三个点位置.由于P、Q是直线l与抛物线的交点，经过解方程组可以求出P、Q的坐标分别为P（m，m-1），Q（m+1，m），本题实际上是一个长度为 2的线段PQ在直线l上移动.因此本小题可以简化为：

如图4，已知P（m，m-1），Q（m+1，m），O（0，0），当m为何值时，△OPQ是等腰三角形.

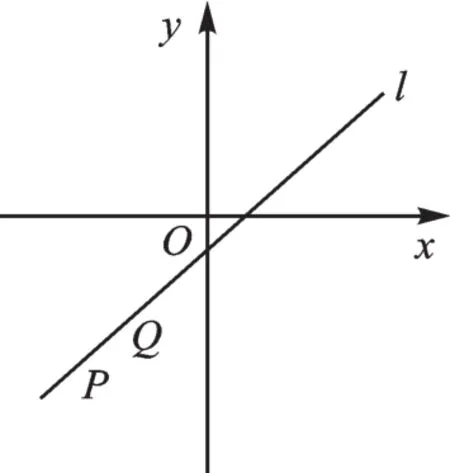
图4

通过这道题目，大家可以发现，后面两个问题经过信息提取，分别得到了一个简化后的题干和简化后的图形.由于没有无效信息的干扰，问题变得非常简单，很容易发现解决问题的思路.

因此对于一道综合题，可能多个小问题共用一个图形.对于每道小题，图形上的所有信息不一定都能用得到，这些信息对于这一小题来说就是无效信息.这些信息保留在图形上，不但对解决这道问题没有帮助，反而干扰解题思路的寻找.因此学会提取题干和图形中的有效信息，简化题干和图形，对于问题的解决是很有帮助的.

请大家试着画出下面这道题的3个小问题中简化之后的题干和图形.

如图5，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，sin∠AOB=反比例函数在第一象限内的图像经过点A，与BC交于点F.

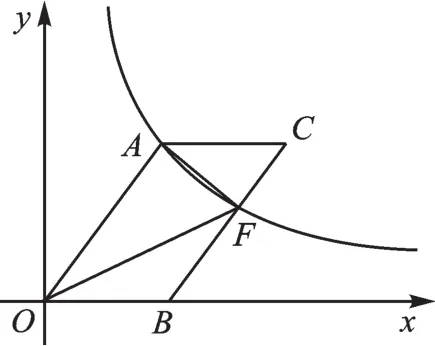
图5

（1）若OA=10，求反比例函数的解析式.

（2）若点F为BC的中点，且△AOF的面积S=12，求OA的长和点C的坐标.

（3）在（2）的条件下，过点F作EF∥OB，交OA于点E（如图6），点P为直线EF上的一个动点，连接PA，PO.是否存在这样的点P，使以P，O，A为顶点的三角形是直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由.

图6