圆锯片切线辊压适张处理的稳态特性研究
2018-05-22张明松
张明松 李 宜 王 勇 伍 强
(三峡大学 机械与动力学院,湖北 宜昌 443002)
0 引 言
在石材切割工程领域,金刚石圆锯片作为主要的切割工具,其在锯切石材的过程中,受到外界激振力的作用容易产生振动,不仅影响石材切割的效率以及质量,而且降低锯片的使用寿命.为了改善圆锯片在切割过程中的振动问题,目前主要采取对圆锯片进行辊压处理的手段来提高圆锯片的振动特性,从而降低圆锯片在切割石材过程中的振动程度[1-3].
目前对圆锯片进行适张处理的方法主要是环形辊压处理法.环形辊压处理可以有效地提高圆锯片高阶的固有频率,同时提高圆锯片的临阶转速来提高圆锯片的振动特性[4-7].但环形辊压处理法存在辊压带附近残余应力集中的现象,这制约着圆锯片经过环形辊压处理后适张效果的进一步提高,环形辊压处理已不能完全满足人们的需求,为此少部分学者开始探索新的圆锯片辊压处理方法,圆锯片切线辊压处理法目前已被少部分学者研究.相关研究结论表明切线辊压强化也是一种提高圆锯片振动特性的有效适张方法,但关于切线辊压强化的研究依然停留在研究辊压残余应力的层面上,对于切线辊压处理的模态分析以及深入对比圆锯片两种辊压处理方法的文章很少.
本文确定了辊压效果的评价指标即锯片的“临界转速”,并理论地推导了利用圆锯片固有频率计算“临界转速”的理论公式,根据圆锯片两种辊压处理的原理分别建立了对应的有限元分析模型,并进行了非线性弹塑性分析以及预应力模态分析,计算了圆锯片经过两种辊压处理后的临界转速,利用临界转速理论同时结合残余应力的分布情况对比了两种辊压处理法的适张效果,为圆锯片不同工况下的适张处理提供理论指导.相比线性的环形辊压适张处理方法,切线辊压适张处理方法不仅能有效改善辊压带附近残余应力集中的不良影响,提升圆锯片的端面平整性,更能提升圆锯片的临界转数,使得圆锯片的切割稳定性更优越.
1 圆锯片临界转速的理论推导
圆锯片的锯切转速在升速以及降速的过程中靠近或者等于锯片的临界转速时,锯片的振幅会急剧加大,甚至会导致锯片失稳,以变量θ表示圆锯片上质点极坐标位移,变量r(r/min)表示圆锯片的转速,t为时间变量,根据分离变量的原则,圆锯片的轴向振动位移可以表示为:
(1)
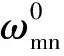
(2)
式(2)说明圆锯片在相同的节圆处具有频率和振型都一样的两个振动模态,且振动的幅值为原系统幅值的一半,其中在节径处的位置方程为:
(3)
进一步解得:
(4)
继续对上式二次时间求导可解得圆锯片各阶振动波的频率计算公式:
(5)
式中,ff为正行波固有频率,fb为反行波固有频率,n为锯片各阶振型节径数,N为锯片的工作转速,fs(N)为以锯片基体为参考体时锯片旋转时的固有频率,可以通过式(6)计算:
(6)
其中,f(N=0)表示当锯片静止不旋转时的固有频率,此时以地面为参考进行观察, 是与锯片工作时的转速有关,称为“离心系数”,可用式(7)表示:
(7)
式中,n为锯片各阶振型节径数,v为锯片基体材料的泊松比.
圆锯片有不止一个临界转速,当圆锯片的运行转速在升速或者降速的过程中靠近锯片某一阶次最小临界转速时,锯片将会因大振幅的振动而失去稳定性,失稳的圆锯片呈现“蝶形”.在实际的锯切过程中,为了提高锯切的效率,工作转速尽量远离最小临界转速,一般小于20%或者更多,在特殊情况下若某二阶的临界转速的间隔相距很远,可以设法将其调至临界转速之间,但要留意在提速或者降速通过临界转速节点的过程中锯片的瞬间大幅振动对锯切过程的影响,应尽量快速通过临界节点,避免不必要的振动对锯片和锯机造成损伤.根据文献[8]有临界转速与固有频率的转换公式:
(8)
式中,ncr为锯片的临界转速,f(N)为锯片N阶模态的固有频率,n为锯片转速,λ为离心系数,mp为泊松比系数(mp=1/v).
2 有限元分析模型的建立
根据切线辊压与环形辊压原理建立有限元分析模型,根据弹塑性薄板问题分析方法,锯片在经过辊压处理后,可视其为一均布载荷作用下的圆形薄板,同时其载荷与支撑条件都是对称的,由前所述的理论模型可知,两种辊压处理的辊压带在圆周上都呈循环对称分布,且辊压载荷在轴向上也是对称分布,故圆周方向上取锯片的一个扇形区域(辊压角度取为30°),轴向方向上取锯片厚度值的一半进行建模.已有研究表明锯齿对圆锯片的辊压处理的适张效果影响很小,故在此忽略锯齿的影响[9-11].锯片的材料特性见表1.
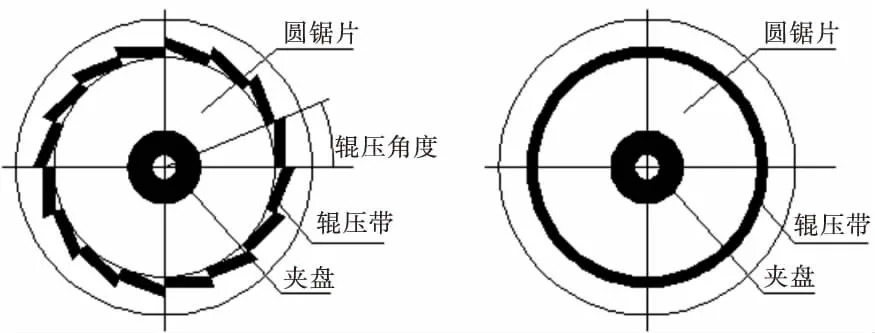
图1 切线辊压(左)环形辊压(右)效果图
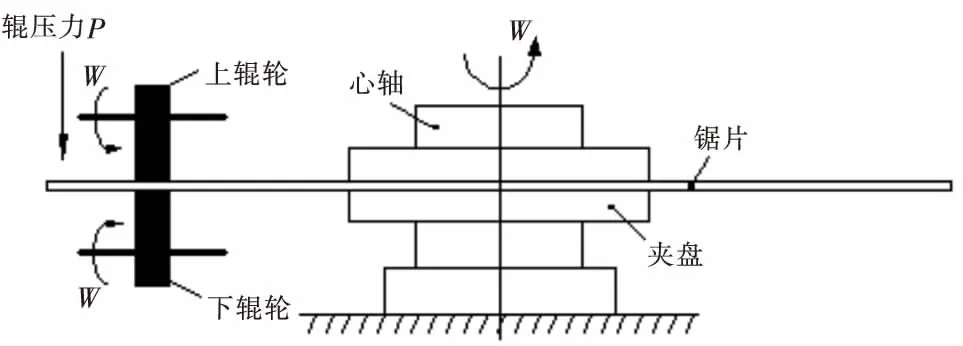
图2 两种辊压处理的原理图

锯片材料锯片外径/mm锯片内径/mm锯片厚度/mm弹性模量/GPa泊松比密度/(kg·m-3)65Mn4256022100.378

表2 两种辊压处理的辊压参数
由于圆锯片的内孔由心轴定位被夹盘夹紧,所以锯片内孔施加全位移约束,采用对称分析的同时还需施加对边界约束,锯片的底面施加轴向方向的位移约束,扇形边界区域施加对称边界约束,采用映射与扫描相结合的方法进行网格划分,单元类型采用solid185,辊压力是通过辊轮的液压系统提供,经过换算对辊压带区域施加均布面载荷,由于圆锯片切线辊压处理的过程中既有弹性变形又有塑性变形,故求解载荷分为两个载荷步,一个模拟辊压力的加载过程,另外一个模拟辊压力的卸载过程,载荷终止时间设置为1 s,子载荷步长时间为0.2 s,最小子载荷时间步长为0.1 s,最大子载荷时间步长为0.3 s,对两种辊压处理进行非线性弹塑性分析,采用多线性随动强化模型,数据填充采用由圆锯片基体材料65Mn的平面应变薄板压缩实验获得的真实应力-应变曲线提供.

图3 环形辊压处理的有限元分析模型 图4 切向辊压处理的有限元分析模型
3 有限元理论结果分析
将圆锯片经两种辊压处理后的切向与径向应力同时向半径方向映射,同时为了研究两种辊压法的变形量大小将径向位移向半径方向映射,如图5所示.

图5 环形辊压与切线辊压残余应力沿半径方向的映射
对比环形辊压与切线辊压残余应力沿半径方向的映射曲线可以看出,环形辊压处理的径向应力在辊压区域以内整体上比切向辊压处理的径向应力要大,在靠近辊压带的区域应力变化不大,在辊压区域以外反而比切向辊压的径向应力要小,在靠近外圆的部分变化不大,且都是在辊压区域以内表现为压应力,在辊压区域以外表现为拉应力;环形辊压处理的径向应力在辊压区域以内外都比切线辊压处理的径向应力要小,且在靠近辊压带附近的地方应力变化较大,这说明环形辊压处理的切向应力在辊压带附近有应力集中现象,且在辊压区域以内外都表现为压应力.

图6 环形辊压与切线辊压径向位移沿半径方向的映射
环形辊压处理以及切线辊压处理都是有效的适张方法,形成的切向应力都是压应力,可以很好地抵消离心应力以及热应力的复合应力在切向上的拉应力,使拉应力尽量在锯片基体内趋于平衡状态.同时环形辊压处理以及切线辊压处理形成的切向应力都在辊压区域以内表现为压应力,在辊压区域以外表现为拉应力,可以很好地抵消热应力以及锯切力复合力在切向上的不利影响.但从残余应力分布的角度看,切线辊压处理的残余应力整体上在辊压带附近的应力集中要小,同时切向应力的平稳性好,同时从图6可以看出,环形辊压处理的幅值较大,在辊压带附近变化更加急促,这不利于锯片的平整性,所以从辊压处理的弹塑性分析的结果来看切线辊压处理的残余应力分布更好,锯片的径向位移更小,更有利于增强锯片的振动特性.
通过圆锯片的稳定性理论可知,辊压处理最终在圆锯片基体内引入残余应力来改变圆锯片各阶的固有频率,从而改变圆锯片的临界转速来达到改善圆锯片振动特性的目的.仅仅从残余应力的角度还不足以对比出两种辊压处理法的优缺点,所以对环形辊压处理进行有限元的预应力模态分析,同样提取前圆锯片前六阶的固有频率,通过模态分析的结果以及圆锯片的临界转速计算公式(8)对两种辊压适张法的临界转速进行计算,结果见表3,图7.
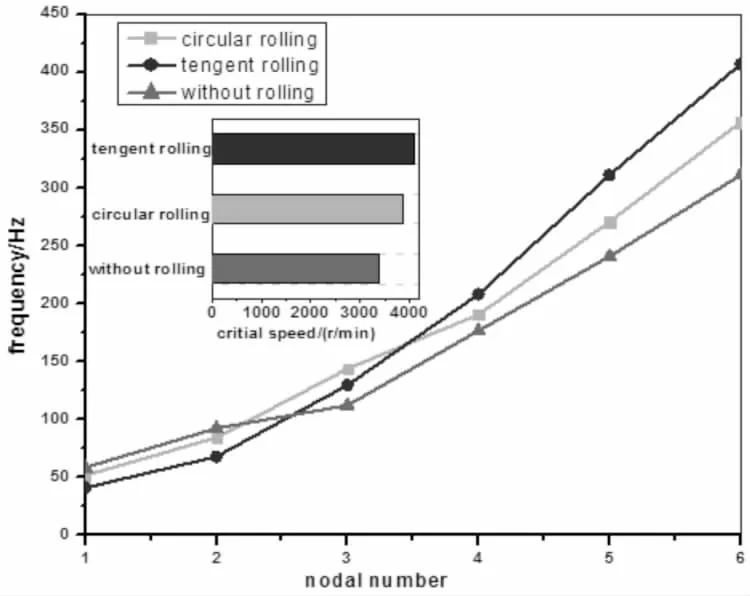
图7 两种强化处理法的各阶固有频率以及临界转速对比

辊压方式f01f02f03f04f05f06ncr/(r·min-1)零适张58.5092.37112.21176.53240.86311.123384环形辊压适张51.6384.21143.78190.42270.77356.633866切线辊压适张40.9467.86129.78208.13311.09407.034100
从环形辊压处理与切线辊压处理的各阶固有频率对比可以看出圆锯片经过两种辊压处理后1、2阶的固有频率都比圆锯片适张之前有所下降,2阶以上的固有频率都比圆锯片适张之前有所增大.同时环形辊压处理在1、2阶固有频率相对于适张之前下降的程度要比切线辊压处理在1、2阶下降的程度要小,且环形辊压处理在3阶固有频率相对于适张之前增大的程度要比切线辊压处理在3阶增大的程度要大;环形辊压处理在3阶以上固有频率相对于适张之前增大的程度要比切线辊压处理在3阶以上增大的程度要小,这说明切线辊压对圆锯片高阶频率的影响更大,结合圆锯片在经过两种辊压处理的临界转速对比图可以看出,切线辊压处理使锯片的临界转速提高了21.15%,大于环形辊压处理的14.24%.综合来看切线辊压处理切线辊压处理的残余应力分布更好,锯片的径向位移更小,锯片端面的平整性更好,对圆锯片高阶频率的影响更大,能较大地提高圆锯片的临界转速,更加有利于提高圆锯片的稳定性,改善圆锯片的振动特性.
4 结 论
首先根据圆锯片环形辊压处理与切线辊压处理的原理建立了有限元分析模型并进行了非线性弹塑性分析以及预应力模态分析,得到了圆锯片在两种辊压处理下的残余应力分布以及各阶固有频率,并根据临界转速计算公式对圆锯片经过两种辊压处理的临界转速进行了计算.对比发现切线辊压处理比环形辊压处理的残余应力分布更好,锯片的径向位移更小,锯片端面的平整性更好,对圆锯片高阶频率的影响更大,切线辊压处理使锯片的临界转速提高21.15%,大于环形辊压处理的14.24%,能较大地提高圆锯片的临界转速,更加有利于提高圆锯片的稳定性,增强圆锯片的振动特性.
参考文献:
[1] 郎西影.金刚石圆锯片切割石材动力学研究[D].沈阳:潘阳建筑大学,2012.
[2] 母德强,崔高健.辊压处理对圆锯片动态稳定性的影响[J].长春工业大学学报(自然科学版),2002,23(S1):9-13.
[3] 耿德旭,王向东,胡 波,等.适张度的辊压加工及对圆锯片的动态性能影响[J].东北电力学院学报,2002,23(2):54.
[4] Stakhiev Y M,Lyzhin F V.Stability of the circular saw blades[J]. Lesn.Zh.1972,15(1):163-168.
[5] Berolzheimer C,Best C. Thin circular saw blad-es[J].Jou-rnal of Forest Production.1959,9(11):404-412.
[6] Parker R G,Jr C D M. Asymmetric tensioning of circular saws[J]. European Journal of Wood and Wood Products,1989, 47(4):143-151.
[7] Schajer G S,Mote C D J. Analysis of optimal roll ten-sioning for circular saw stability[J]. Wood & Fiber Science,1984,16(3):323-338.
[8] Ante Skoblar,Nikola Andjelic,Roberto Zigulic. Determination of Critical Rotation Speed of Circular Saws from n-atural frequency of annular plate with annular plate with analogous dimensions[J].International Journal for Quality Research,2016,10(1):177-192.
[9] 母德强,崔高健,陈塑寰.辊压适张度处理对圆锯片临界转速的影响[J].机械工程学报,2001,37(9):30-33.
[10] 母德强,陈塑寰.圆锯片最佳辊压适张度处理位置的分析[J].林业科学,2001,37(2):84-89.
[11] 钱 桦.木工圆锯片制造过程中的残余应力研究[D].北京:北京林业大学,2004.
