基于PFC3D的破裂岩样力学行为及其影响因素研究

王 晨 高 玮 葛明明 贺天阳

(1. 河海大学 土木与交通学院， 南京 210098；2. 河海大学 岩土力学与堤坝工程教育部重点实验室， 南京 210098；3. 江苏省昆山市城区建设管理处，江苏 苏州 215300)

随着我国经济和技术的不断进步，地下工程向深部发展成了必然趋势[1]．和浅部工程不同，深部工程开挖后围岩一般分为3个区，即破裂区、塑性区、弹性区，而破裂区的围岩位移占总位移量的85%～95%，所以破裂区的支护是维持围岩稳定的关键[2]．

由于破裂区的岩体已成为非连续介质，力学分析比较困难，目前对它的研究尚不多，已有成果大多是室内试验研究．主要有，朱建明[3]分别对闪长玢岩与矽卡岩进行三轴压缩试验，研究了破裂岩体的损伤演化规律，发现其损伤是由塑性应变引起的，而与弹性应变无关；牛双建[4]通过完整砂质泥岩试样的加卸载试验，制得不同破裂程度的损伤岩样，再分别将其置于不同围压下进行三轴试验，发现随着初始损伤岩样的破裂程度增大，其峰值强度、内摩擦角与粘聚力均大幅度减小；宗义江[5]通过对不同破裂程度的岩样进行三轴压缩蠕变试验，发现随着岩样破裂度的增大，其弹性模量、峰值强度和残余强度均大幅降低，岩样的力学性质从应变软化逐渐向应变硬化转变；韩立军、贺永年[6-7]等在运用金属套管给破裂岩样施加环向有效约束的条件下进行加载试验，发现破裂岩体在约束下具有良好的结构效应，且破裂岩体的再破坏不会导致最终极限承载能力的降低和变形量的显著增加．综上所述，目前研究尚缺乏对破裂岩体力学行为的系统研究和具体分析，而通过数值模拟可以克服一些因技术水平而导致的室内试验难点，从而全面的研究问题．因此，本文基于PFC3D软件建立了破裂岩样的数值模型，研究了其基本力学行为，并对力学行为的主要影响因素进行了系统分析．

1 破裂岩样基本力学行为研究

1.1 模型的建立

本次研究以宗义江的室内试验[5]为基础．首先根据完整岩样的单轴试验结果(见表1)，运用PFC3D软件进行模拟，标定出模拟完整试样需要的微观参数．

表1 完整岩样单轴压缩试验结果

其中保持数值模型的尺寸与室内试验一致，即直径50 mm，高100 mm的圆柱体试件．数值试验最终标定的微观参数见表2．

表2 模型的微观参数

此时PFC3D模拟的完整岩样单轴压缩应力-应变曲线与室内试验曲线对比情况如图1所示．

图1 数值模拟和室内单轴试验应力-应变对比图

将表2中的微观参数用于岩样的数值模拟，然后根据室内加卸载试验得到的破裂岩样裂纹的位置设置节理面，使完整岩样转变为破裂岩样，再通过调节节理面的粘结强度，使模型在指定围压(5，10，15，20 MPa)下达到的峰值强度与室内试验一致，观察其应力-应变曲线，得到破裂岩样的力学行为．其中，室内试验选取峰后强度为峰值强度70%时卸载制得的破裂岩样，其破裂程度对应于隧道开挖后围岩的松动区[5]，模型标定的节理面粘结强度为1 000 MPa，裂纹分布如图2所示(图2(b)中黑点为离散点，未能完全过滤干净)．

图2 试验岩样[5]与模型对比图

1.2 模拟结果分析

将建好的数值模型分别在不同围压下进行试验，得到不同围压下的应力-应变图如图3所示．

图3 不同围压下数值模拟与室内试验应力-应变对比图

从图3可以看出，数值模拟和室内试验结果均吻合较好，尤其是在低围压5 MPa条件下(因此下面模拟研究均在低围压下展开)．说明PFC3D软件可以较好的模拟破裂岩样的力学行为，其可靠性可以得到保证．但是，数值模拟结果在一定条件下和试验曲线存在差异，其表现和原因分析如下：从图3可以看出，无论在低围压还是高围压下，在峰值前初始阶段，数值模拟破裂岩样的变形模量均高于相同围压下室内试验的变形模量，这是由于模型只是近似模拟了一些较大裂隙，真实岩样中还存在许多微观裂缝，这导致了模型变形模量普遍偏大．峰值后变形模量随着围压的变大而减小，说明在高围压下，初始阶段孔隙更加容易压密，棱角更容易磨平，在峰后进入近似塑性阶段，变形模量几乎为零．由于模型的部分微观参数是基于峰值强度调整的，所以两者间峰值强度相差不大．峰值后应力-应变曲线在低围压下出现了较明显的应力强化现象，但模型最终的强度没有达到峰值强度，这点与室内试验有较明显区别，分析其原因为，室内试验采用的钢板刚度较大，约束能力强造成应力后期发展高于峰值应力，但是其规律基本一致；在高围压下，模型和室内试验的峰后应力-应变曲线均没有较明显的应力降，应力维持在很高的水平，但应力强化现象没有室内试验明显，这是由于颗粒之间与实际块体之间存在一定的差别，在高围压下，大部分颗粒间粘结在峰前阶段就已破坏，峰后类似于理想塑性体，而岩石块体则不会破裂成碎散的颗粒体，因此，峰后仍会出现应力强化现象．

最后，由图3可知，在低围压下PFC3D软件模拟结果与室内试验所得的应力-应变曲线吻合的很好，可靠性较高，因此，下面模拟研究均在低围压(5 MPa)下展开．

2 破裂岩样力学行为的影响因素分析

2.1 影响因素的确定

朱建明[3]对两类不同岩性的破裂岩样进行的三轴压缩试验结果如图4所示．从中选取两条相近围压下(硬岩20 MPa和软岩15 MPa)的应力-应变曲线进行对比，可以发现，硬岩峰后有明显的应力降，而软岩在围压15 MPa时已无明显的应力下降，基本维持在一定的应力水平．此现象说明，在相同围压下，不同岩性的岩样力学行为差异很大，因此，岩性应该是影响破裂岩样力学行为的主要因素之一．

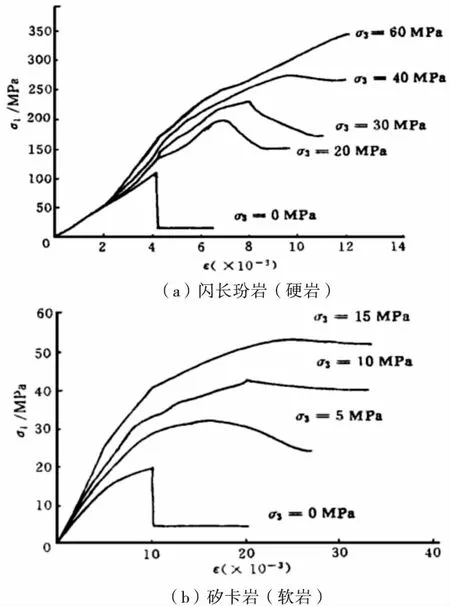
图4 不同围压下两类破裂岩样的全应力-应变曲线[3]

另外，牛双建[4]通过控制不同峰后卸载点制得了不同破裂程度的破裂岩样(卸载点百分比越高，对应的岩样破裂程度越小)，并将其置于不同围压下进行了三轴试验．对其结果进行整理，部分结果见表3．通过对比相同围压下的峰值强度，可以发现不同破裂程度下的峰值强度差异很大，因此，破裂程度也应该是影响破裂岩样力学行为的一种主要因素．

表3 不同围压下损伤岩样峰值强度值

由以上对前人试验结果的总结分析，可以发现岩性与破裂程度是影响破裂岩样力学行为的两种主要因素．此外，根据岩石力学基本原理，岩石微观孔隙量及破裂面方向会对破裂岩样力学行为产生较大影响，且试验中的加载速率也会对试验结果产生影响，但室内试验由于试验条件、操作可行性等原因，几乎没有体现出这些方面的影响，而借助数值软件则可以较简单的对各种因素进行研究，因此，本次试验针对以上5种因素进行系统分析．

2.2 影响规律研究

将依次分析岩性、破裂程度、孔隙量、加载速率和破裂面方向对破裂岩样力学行为的影响规律．

2.2.1 岩性的影响

第二，大学生创客教育拒绝填鸭式教学，追求体验式学习。随着网络技术的发展，教育的普及程度也有了较大提高，传统教育教学模式发生了改变，大学生的学习模式也受到影响。传统的书籍、课本等知识渠道的使用率逐渐降低，基于网络信息的知识渠道使用率随之提升，这样的情况下，大学生的知识结构更加复杂化，其学习需求发生了改变，如果教师依旧采用填鸭式教学，那么教学效果和教学效率就会受到影响，教师要充分考虑当前大学生对体验式学习的追求，加强教学实践性，展开多样化的教学活动，加强和学生的沟通，从而帮助学生更好地展开创客活动。

研究通过调整模型颗粒的刚度和粘结强度来模拟不同岩性的破裂岩样，并将应力-应变曲线中的弹性模量作为代表性参数来近似反映岩性的好坏，其中弹性模量越大，表明岩性越好．岩样对应的弹性模量分别为2.5、7.7、10.5、11.6 GPa，可近似依次对应石膏、泥灰岩、炭质砂岩、大理岩．对应的加载应力-应变曲线如图5所示．

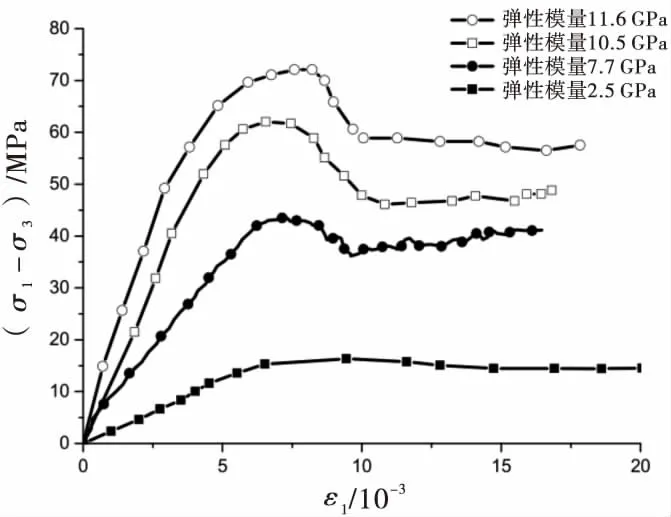
图5 岩性不同的应力-应变图

由图5可以看出，随着岩性的变好，峰值强度逐渐增大，但峰后应力降低值也同时逐渐变大，因此，深部地下工程围岩岩性越好，开挖后更要防范破裂区岩体因再破裂导致的应力下降．比较图中炭质砂岩(10.5 GPa)和石膏(2.5 GPa)两类岩样，最主要的区别在于峰后，低围压下岩性较好的岩样，由于内部破裂面的存在，应力有所起伏，但总体表现为下降的趋势；岩性较差的岩样则没有出现应力下降的现象，这与朱建明进行的三轴压缩试验结果(图4)[3]吻合，从而验证了数值模型的有效性．

选取弹性模量作为衡量岩性好坏的依据，峰值应力和特征点应力(峰后应力最低点)与岩性(弹性模量)关系如图6所示．从图6可看出，峰值应力与特征点应力均呈线性增大，但随着岩性的变好，峰后应力下降值越来越大．

图6 岩性不同的峰值点与特征点分布图

2.2.2 破裂程度的影响

本次研究主要通过改变模型节理的粘结强度，用粘结强度的强弱来间接模拟破裂岩样的破裂程度．图7为保持其他条件不变时，改变节理面粘结强度所得应力-应变曲线图，其中，节理面粘结强度分别取100、500、1 000和2 800 MPa(模型初始的节理面粘结强度为1 000 MPa，颗粒间粘结强度为2 800 MPa)，粘结强度越大代表破裂程度越小．

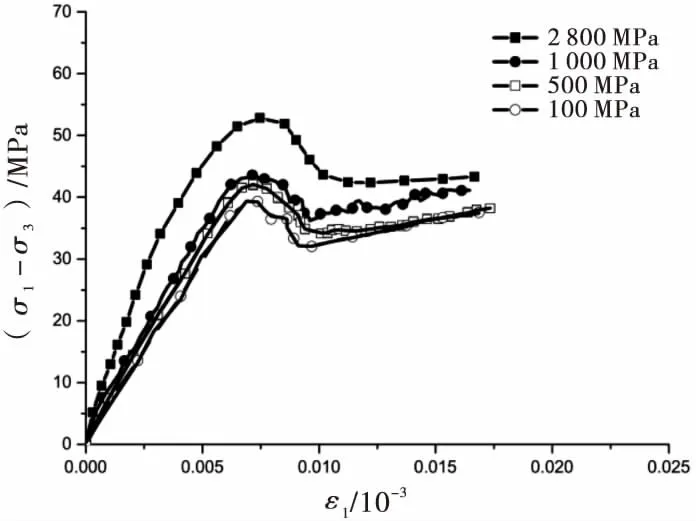
图7 节理面粘结强度不同的应力-应变图

从图8可以看出，在峰值前，随着破裂程度的减小，峰值强度和变形模量逐渐变大，但峰值应力所对应的轴向应变值几乎没有改变；峰值后，破裂程度大的岩样变形模量较大，这是由于内部孔隙多，孔隙被破碎的岩石填充后，整个岩样强度更容易提高所致．峰值应力和特征点应力与破裂程度(粘结强度)关系如图8所示．从图8可看出，峰值强度与破裂程度呈线性关系，破裂程度越小，峰值强度越大；当节理面强度趋近2 800 MPa时，特征点应力变化幅度减小，最终趋于不变．

图8 破裂程度不同的峰值点与特征点分布图

此外，粘结强度的不同也可认为是注浆加固浆液粘结强度的差别，由图7可知，浆液粘结强度越大，破裂岩样整体刚度越大，且其粘结强度越接近加固体强度，加固效果越好．但超过加固体本身强度时，自身承载力几乎不再增加，如图9所示．

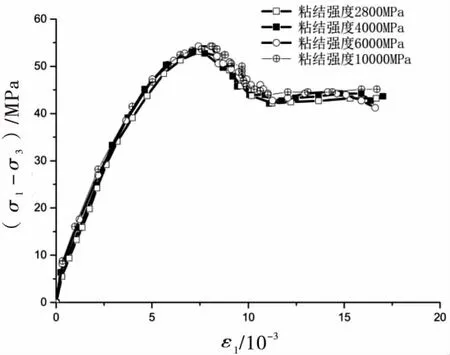
图9 粘结强度超过加固体的应力-应变图

2.2.3 孔隙量的影响

在其他微观参数不变的情况下，将孔隙体积与总体积之比分别设置为0.3、0.35、0.4和0.45，模型包含的颗粒体数分别为4 783、4 271、2 733和2 286．其模拟计算结果如图10所示．由图10可以看出，孔隙量越多的岩样在峰后出现应力强化的趋势越明显，其主要原因是其内部空隙大，岩样较容易被压密，且其初始强度较低，因而更容易出现应力强化现象．

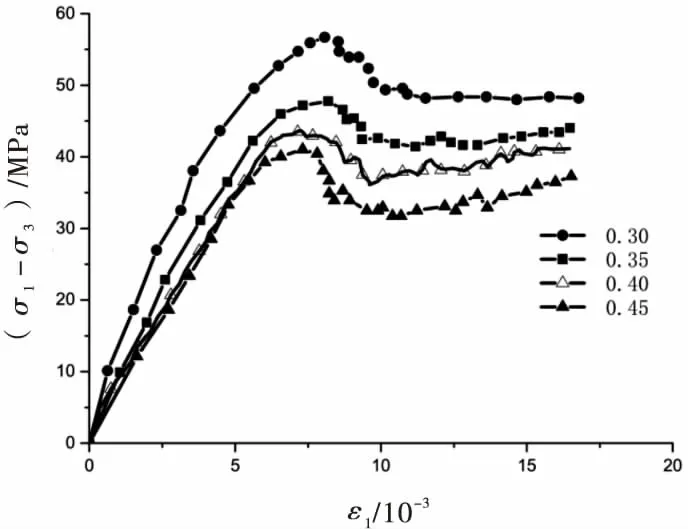
图10 孔隙量不同的破裂岩样应力-应变图

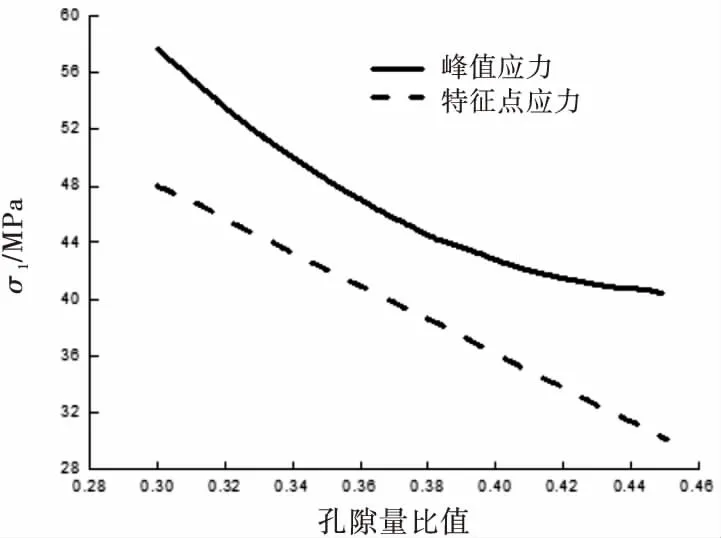
图11 孔隙量不同的峰值点与特征点分布图

2.2.4 加载速率的影响

保持其他条件不变，通过控制墙体、颗粒体外力、颗粒体速度和混合受力来确定加载过程，分别采用不同的加载速率，依次为0.1、0.3、0.6和1.0 MPa/s，得到的结果如图12所示．

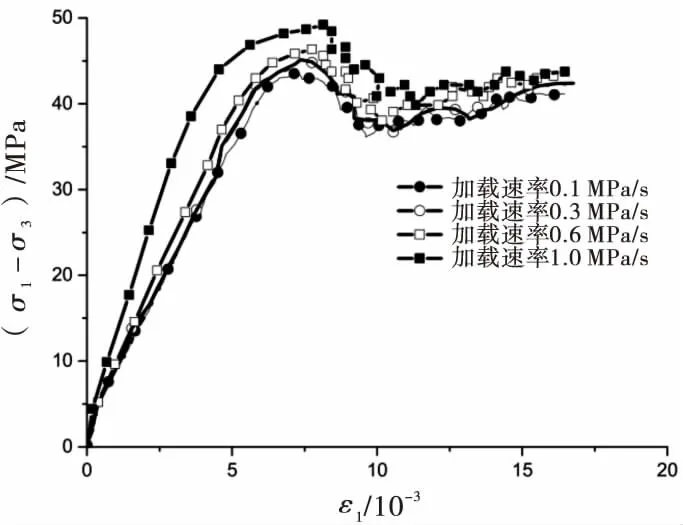
图12 不同加载速率下破裂岩样的应力-应变图

从图12可以看出，在峰前阶段，随着加载速率的增大，峰值应变和峰值强度均逐渐变大，这是因为岩样破裂后颗粒在加载速率较快时，空隙被颗粒填充的速度较快，因而，裂纹发展被抑制，发展不充分．峰值应力和特征点应力与加载速率的关系如图13所示．

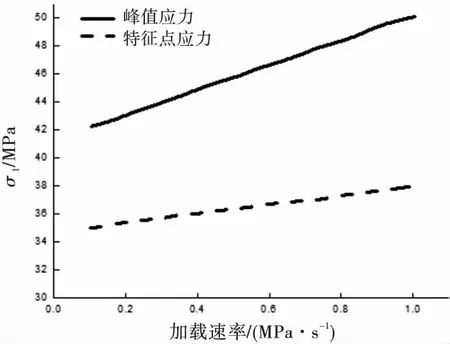
图13 加载速率不同的峰值点与特征点分布图

由图13可知，随着加载速率的增加，峰值应力和特征点应力均线性增大，且峰值应力增大的速率明显快于特征点应力，说明加载速率对峰值前影响更大．

2.2.5 破裂面方向的影响

研究通过改变破裂面与水平面的夹角θ来模拟破裂面的位置，因此，将此夹角作为破裂面方向影响的代表性参数．试验将内部复杂的破裂面简化为与水平面夹角分别为90°、60°、45°和20°的4条平行破裂面，具体分布情况如图14所示．

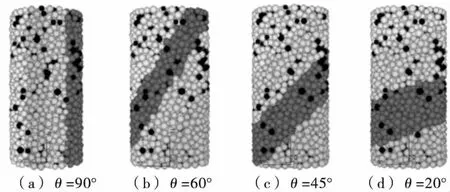
图14 破裂面分布详图

数值模型计算结果如图15所示．从图15可以看出，峰值应力、应变均随着夹角的增大而减小，但最终的残余应力相差不大，且在弹性阶段其变形模量近乎一致．其中，夹角为90°的破裂岩样类似于室内试验的张拉破坏，强度损失最为明显．

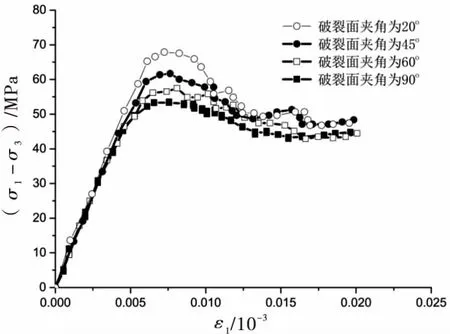
图15 破裂面方向不同岩样的应力-应变图

得到峰值应力和特征点应力与破裂面位置关系如图16所示．由图16可知，随着夹角θ的增大，峰值应力值减小并趋于不变，特征点应力呈线性减小．

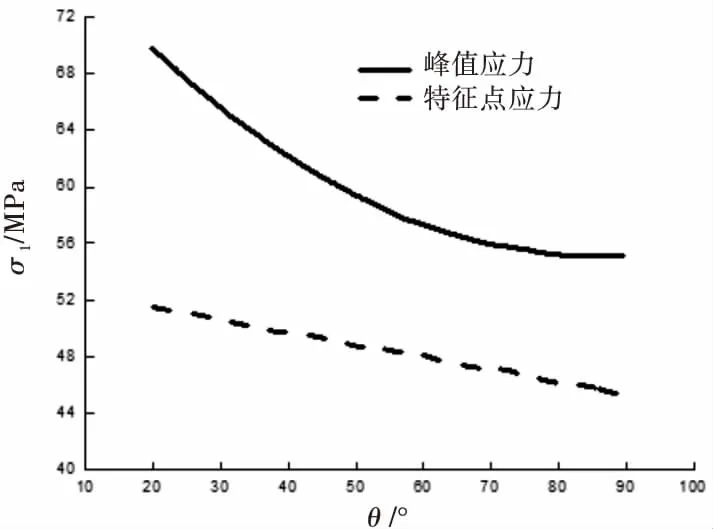
图16 破裂面方向不同的峰值点与特征点分布图

2.3 影响因素敏感性分析

灰色关联分析法能够对量纲不同的诸因素进行分析比较，研究各个因素对结果的影响程度，实用性很强．为了进一步研究上述各因素对破裂岩样力学行为的影响程度，本文将峰值强度作为代表性参数来反应其力学行为，通过灰色关联分析法[8]计算了它与各影响因素间的关联度，来间接研究敏感性．最终结果见表4．

表4 敏感系数汇总表

由表4可以看出，破裂程度、岩性及加载速率与峰值强度的关联度很强，均在90%以上，因此，三者是主要影响因素，而孔隙量和破裂面方向关联度不高，均在50%以下，二者为次要影响因素．其中，破裂程度对破裂岩样力学行为影响最严重，岩性和加载速率影响次之且相同，而孔隙量影响最小，破裂面方向的影响稍大于孔隙量．因此，以后的研究中建议把破裂程度、岩性及加载速率的影响作为主要目标．

3 结 论

本文通过离散元软件PFC3D对破裂岩样进行数值模拟试验，研究其基本力学行为，并在低围压条件下对主要影响因素进行了分析，得出以下结论：1)不同岩性的破裂岩样，其加载应力-应变曲线主要区别在于峰后，低围压下岩性较好的岩样，总体表现为下降的趋势；岩性较差的岩样，则没有出现应力下降的现象．2)破裂岩样的力学行为与破裂程度有关．破裂程度越小的岩样，变形模量和峰值应力越大，且峰后的变形模量越大．另外，岩样注浆加固时，随着浆液粘结强度的增大，岩样加固效果更加明显，但当超过加固体自身强度后，自身承载力几乎不再增加．3)低围压下随着孔隙量的增加或破裂面与水平面间夹角的增大，破裂岩样的峰值应力逐渐减小，最终趋于不变，而特征点应力则线性减小．4)破裂岩样在不同加载速率下，随着加载速率的增大，应力-应变曲线屈服段变长，峰值应力和特征点应力均线性增大，且峰值应力增大的速率明显快于特征点应力．5)通过灰色关联分析法发现：破裂程度对破裂岩样力学行为影响最严重，岩性和加载速率影响次之，三者均是主要影响因素；而破裂面方向的影响稍大于孔隙量，孔隙量影响最小，均为次要影响因素．因此，以后的研究中建议把破裂程度、岩性及加载速率的影响作为主要目标．

参考文献：

[1] 何满潮，谢和平，彭苏萍，等．深部开采岩体力学研究[J]．岩石力学与工程学报，2005，24(16):2803-2813．

[2] 靖洪文．深部巷道大松动圈围岩位移分析及应用[M]．徐州:中国矿业大学出版社，2001．

[3] 朱建明，徐秉业，任天贵，等．基于三轴压缩试验的破裂岩损伤演化方程的建立[J]．工程地质学报，2000，8(2):175-179．

[4] 牛双建，靖洪文，杨旭旭，等．深部巷道破裂围岩强度衰减规律试验研究[J]．岩石力学与工程学报，2012(8):1587-1596．

[5] 宗义江．深部破裂围岩蠕变力学特性与本构模型研究[D]．徐州：中国矿业大学，2013．

[6] 韩立军，贺永年，蒋斌松，等．环向约束条件下破裂岩体力学特性试验研究[J]．中国矿业大学学报，2006，35(5):617-622．

[7] 韩立军，贺永年，蒋斌松，等．环向有效约束条件下破裂岩体承载变形特性分析[J]．中国矿业大学学报，2009，38(1):14-19．

[8] 孙玉刚．灰色关联分析及其应用的研究[D]．南京：南京航空航天大学，2007．