吸力式桶型基础水平静力加载试验承载特性与稳定性分析

许建朋 陈旭光 姜育科

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室， 南京 210098； 2. 河海大学 江苏省岩土工程技术工程研究中心， 南京 210098)

由于全球能源危机、环境污染以及温室效应的加剧，海上风能作为一种重要可再生、清洁能源逐渐受到人们的关注，海上风电得到大力发展．而在复杂海洋环境下，海上风电基础的承载特性与稳定性直接影响到海上风电整体的结构安全．

吸力式桶型基础[1]为上端封闭下端开口的筒体，可利用负压原理下贯至海底土层．近年来，由于其成本较低、安装方便、可回收利用的特点被广泛应用于海上风电基础．目前，国内外学者对于吸力式桶型基础已经有一定程度的研究．Byrne[2]基于牛津大学研制的加载系统，研究了吸力式基础在砂土中的承载力特性，采用水平和竖向的静载和循环荷载等组合荷载，得到吸力式基础的破坏包络面．Chen[3]比较了吸力式沉箱在正常固结和超固结土中的一系列离心机模型试验的结果，分析了其在静载和循环荷载作用下的抗拔承载力．Randolph[4]论述了水平和竖向荷载条件下粘土中吸力基础的分析技术和设计参数．讨论了水平和竖向荷载之间的相互作用，并且考虑诸如土壤的强度各向异性和施加的载荷对吸力式沉箱的水平承载力的影响．朱斌等[5]对吸力式沉箱在饱和淤泥中的吸力安装和横向承载力进行大型模型试验．试验结果表明：渗流效应影响基础在淤泥中的下沉，沉贯所需的吸力可以根据桶壁摩擦力和锥阻力很好地预测．李大勇等[6-8]对饱和细砂土中裙式吸力基础的承载力特性开展模型试验研究，试验选取不同裙高的吸力基础进行水平静力加载试验，分析了水平位移和土压力的变化．王建华[9]通过模型试验研究了桶形基础在竖向静载以及水平循环荷载共同作用下的承载特性，并与有限元计算结果相对比，发现竖向静载决定了吸力锚失稳时循环荷载的大小与次数．

由此可见，国内外学者对吸力式桶型基础已经有了初步的研究，本文对吸力式桶型基础进行水平静载模型试验，并且对试验结果进行无量纲化处理，研究其承载特性以及稳定性的变化规律．

1 吸力式桶型基础模型试验

1.1 吸力式桶型基础模型

吸力式桶形基础模型由主桶模型和加载杆固定端组成，加载杆固定端设置在主桶模型顶盖中央，如图1所示．模型的材料是圆钢，并打磨光滑，下部敞开，上部顶盖一侧设有排水孔．本文模型试验采用3个不同长径比的吸力式桶形基础模型，尺寸见表1．

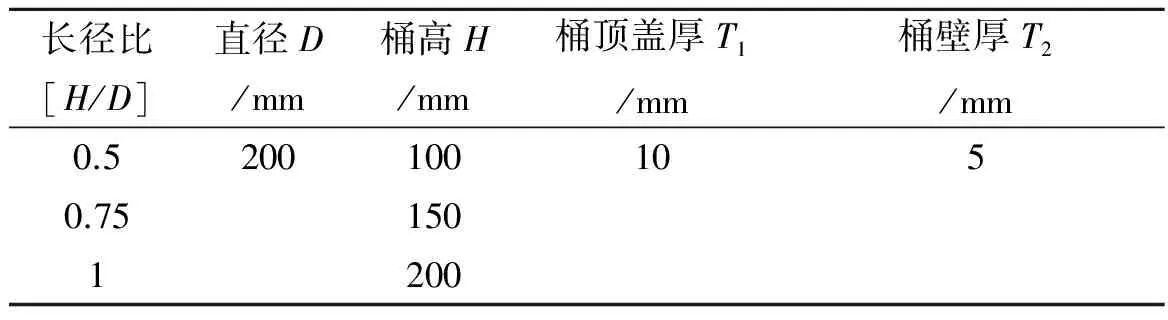
表1 桶形基础模型尺寸

图1 吸力式桶形基础模型

1.2 试验地基

试验所选地基为取自海滩的细砂土，颗粒级配如图2所示，其物理力学参数见表2．为保证试验过程中砂土地基的均质性，采用分层装填，同时采用渗流加静置固结，可以加速砂土固结．每次装填砂土10 cm，注水并使水位高于砂土，打开排水阀进行排水，利用渗流作用加速砂土固结．重复上述过程，最终完成40 cm高砂土地基的分层填筑．

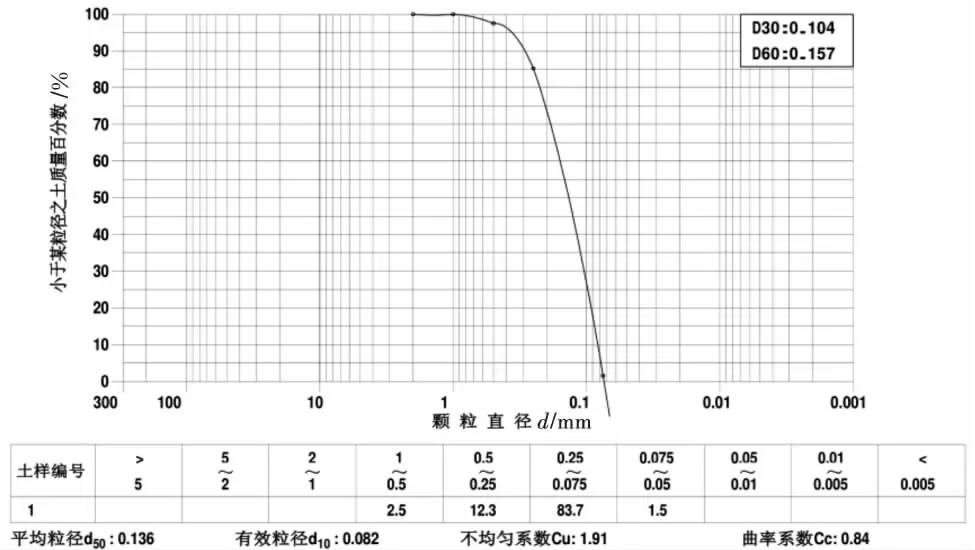
图2 砂土颗粒级配曲线

类型比重孔隙比渗透系数/(cm·s-1)细砂2．520．5740．002

1.3 水平静力加载试验方案

图3为水平静力加载模型试验方案示意图．

图3 水平静力加载模型试验方案示意图

吸力式桶形基础模型及微型土压力计埋入砂土中；2只LVDT位移传感器沿水平方向布置在加载杆受力方向后侧，分别标记LVDT1和LVDT2，LVDT1距离基础模型顶盖高90 cm，LVDT2距离基础模型顶盖高80 cm；静力加载高度是50 cm．水平静力加载模型试验，用砝码逐级加载，每级荷载为2 N，每级荷载作用下LVDT读数没有变化或者变化小于0.01 mm时，继续施加下一级荷载，直至基础模型失稳破坏．重复试验过程，直到完成3个不同长径比的吸力式桶形基础模型试验．

2 水平静力加载模型试验位移试验结果分析

将试验结果均做无量纲化处理[10]：水平荷载的无量纲表达式为F/2πR3γ、其中F为水平静力，R为吸力式桶形基础模型半径，γ为试验砂土有效重度(由第二章土体参数算得9.46 kN/m3)；基础水平位移的无量纲化表达式为s/D，s为LVDT所测基础水平位移量，D为吸力式桶形基础模型的直径；基础桶顶位移的无量纲化表达式为S/D，S为基础桶顶水平位移量，D为吸力式桶形基础模型的直径；基础转动点位置的无量纲化表达式为h/H，h为转动点到桶形基础顶面之间的距离，H为吸力式桶形基础的长度(高度)．

2.1 水平静载作用下吸力式桶形基础的荷载位移关系

如图4所示为无量纲化下基础长径比分别为0.5、0.75和1时，吸力式桶形基础LVDT2处水平位移和水平荷载的关系曲线．

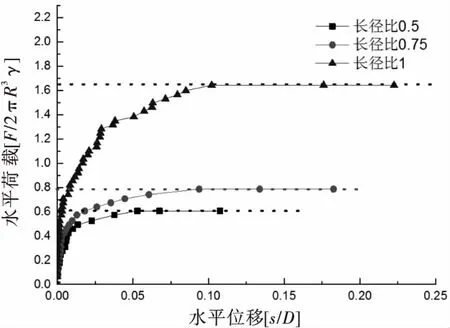
图4 不同长径比的吸力式桶形基础水平荷载-位移曲线图

由图4可知：对于不同长径比的吸力式桶形基础水平荷载-水平位移关系曲线的趋势基本相同，都可以分为3个阶段(弹性变形阶段、塑性变形阶段和失稳破坏阶段)，分析过程基本一致，将基础能承受的最大荷载定义为水平极限承载力．由图可知：长径比为0.5、0.75和1的吸力式桶形基础水平极限承载力分别为0.6、0.79和1.64．

2.2 水平静载作用下吸力式桶形基础筒顶位移与荷载关系

水平荷载作用下，假定吸力式桶形基础倾覆失稳时的运动形式是绕着基础中心轴上的某一点发生转动[11]，水平静力加载试验中，2支LVDT位移传感器沿水平方向布置在加载杆受力方向后侧，可计算基础桶顶水平位移随荷载的变化关系．无量纲化下不同长径比的吸力式桶形基础桶顶位移随水平荷载变化曲线图如图5所示．

图5 不同长径比吸力式桶形基础桶顶随水平荷载变化关系

从图5可以看出，随着水平荷载的增加，在相同荷载水平下长径比大的基础桶顶水平位移量小于长径比小的位移量；达到极限水平荷载时，长径比为0.5、0.75和1所对应的桶顶水平位移量分别约为0.029、0.038和0.05，说明随着长径比的增加，基础能承受的变形量增大，基础桶顶极限水平位移量增加；当达到极限水平承载力时，吸力式桶形基础的水平位移一直增大，此时基础失稳破坏．

按照破坏时基础最大水平位移量达到基础宽度的3%～6%作为水平位移破坏的标准[10]，可知实验结果基本与之吻合．

2.3 吸力式桶形基础转动点变化规律

水平荷载作用下，假定吸力式桶形基础倾覆失稳时的运动形式是绕着基础中心轴上的某一点发生转动[12]，水平静力加载试验中，2支LVDT位移传感器沿水平方向布置在加载杆受力方向后侧，可计算转动点的位置随水平荷载的变化关系．

图6所示为无量纲化下不同长径比的吸力式桶形基础转动点随荷载变化曲线图，其中负号表示转动点在砂土表面以下．由图6可以看出，随着水平荷载的增大，基础转动点会向下移动，最后会趋于一个稳定的范围．吸力式桶形基础受到水平荷载作用时，主要的运动方式为转动，也会发生平动；结合基础荷载-位移曲线图分析，基础在弹性变形阶段和塑性变形前期阶段，由于基础变形位移量相对较少，平动所占的比例相对较大，所以转动点的位置变化较大；随着塑性变形的发展到失稳破坏阶段，基础的变形位移量逐渐增大，基础主要以转动为主，并逐渐成为完全转动，所以转动点的范围趋于一个稳定的范围．

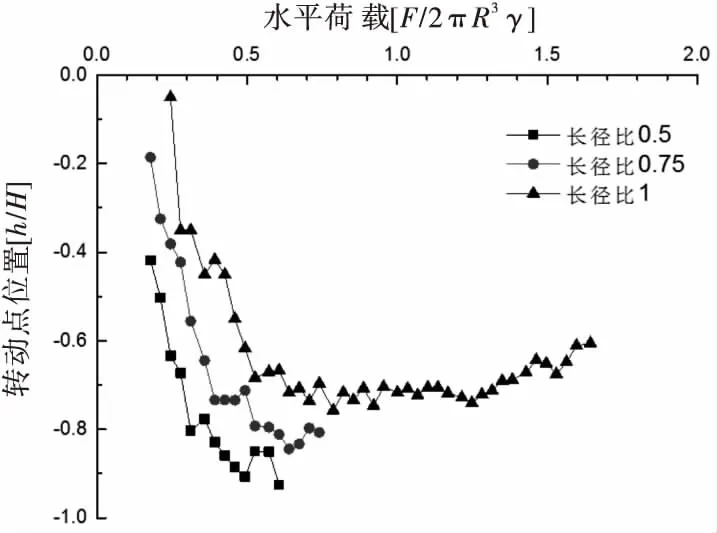
图6 不同长径比吸力式桶形基础转动点随荷载变化曲线图

3 水平静力加载模型试验土压力试验结果分析

吸力式桶形基础属于埋深小的宽浅式基础，基础前后侧受到的土压力按主动土压力和被动土压力考虑[13-14]．所测得的被动土压力是正值，测得的主动土压力是负值．通过土压力值的测量，得出被动土压力区和主动土压力区，并将相同埋深的基础前后侧土压力值相减，得到土压力的合力，土压力合力为0处则为基础转动点位置[15]．

3.1 不同长径比吸力式桶型基础转动点位置

图7～9分别为为长径比0.5、0.75、1的吸力式桶形基础土压力合力分布图．从图7可知：长径比为0.5的吸力式桶形基础的转动点位置在0.85倍桶高以下，在失稳破坏时会稍微向上移动，转动点位置的平均深度约为0.9倍桶高．从图8可知：长径比为0.75的吸力式桶形基础的转动点位置在0.7～0.9倍桶高之间，在失稳破坏时会稍微向上移动，转动点位置的平均深度约为0.8倍桶高．从图9可知：长径比为1的吸力式桶形基础的转动点位置0.6～0.65之间，转动点平均位置约为0.62倍桶高．

图7 长径比0.5的吸力式桶形基础土压力合力分布图

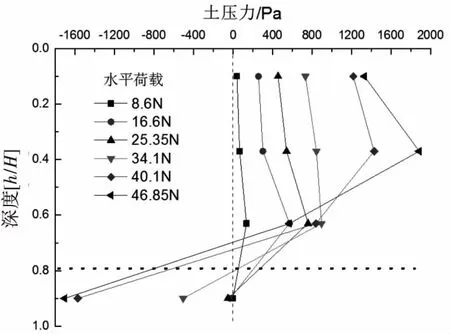
图8 长径比0.75的吸力式桶形基础土压力合力分布图

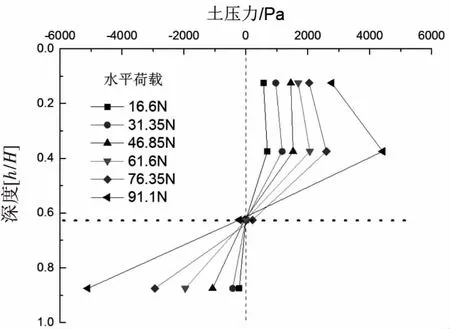
图9 长径比1的吸力式桶形基础土压力合力分布图

3.2 位移与土压力得到的转动点位置对比

将2.3节位移分析得出无量纲化下吸力式桶形基础破坏时的转动点位置和3.1节土压力分析得到的数据汇总并对比，见表3．

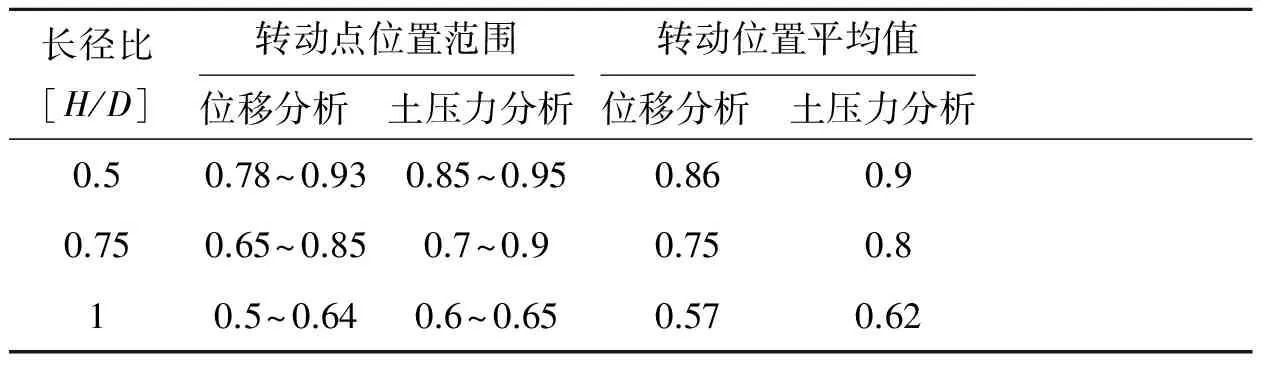
表3 不同长径比的吸力式桶形基础转动点汇总

由表3可知，通过位移分析和土压力分析得到的转动点位置差别不大，基本吻合．综合分析可知：水平静载作用下，长径比0.5的吸力式桶形基础的转动点位于基础顶面以下0.78～0.95倍桶高之间，长径比0.75的吸力式桶形基础的转动点位于基础顶面以下0.65～0.9倍桶高之间，长径比1的吸力式桶形基础的转动点位于基础顶面以下0.5～0.65倍桶高之间．随着基础长径比的增大，基础转动点的位置相对于桶高向上移动，但是都位于基础顶面以下0.6～0.9倍桶高之间．

4 结论与建议

本文通过无量纲化方法对吸力式桶形基础水平静力加载模型试验的结果进行详细分析．主要得出以下结论：

1)吸力式桶形基础在水平静力加载过程中分为3个阶段：弹性变形阶段、塑性变形阶段和失稳破坏阶段．吸力式桶形基础的承载力和稳定性随长径比的增大而增大．

2)不同长径比的吸力式桶形基础在水平静力加载过程中弹性变形阶段，桶顶水平位移量基本相同，均为0.004；桶顶极限水平位移量随着长径比的增大而略有增大；实验结果基本吻合整体刚性短桩水平承载破坏特性．

3)通过位移和土压力分析分别得到的基础转动点位置变化规律，两者差别相对较小；随着基础长径比的增大，基础转动点的位置相对于桶高向上移动，但是都位于基础顶面以下0.6～0.9倍桶高之间．本文所得结论均为实验室内进行，还需要数值模拟或理论分析的验证．

参考文献：

[1] Ibsen L B. Implementation of a New Foundations Concept for Offshore Wind Farms[C]. Proceedings Nordisk Geoteknikermøte nr. 15: NGM 2008， Nordisk Geoteknikermøte, Sandefjord, 2008：19-33．

[2] Byrne B W. Investigations of Suction Caissons in Dense Sand[J]． University of Oxford, 2000．

[3] Chen W, Randolph M. Radial Stress Changes Around Caissons Installed In Clay By Jacking And By Suction[C]．2004．

[4] Randolph M F, House A R. Analysis of Suction Caisson Capacity in Clay[C]． Offshore Technology Conference, 2002．

[5] Zhu Bin, Kong Deqiong, Chen Renpeng, et al. Installation and Lateral Loading Tests of Suction Caissons in Silt[J]． Canadian Geotechnical Journal, 2011, 48(7):1070-1084．

[6] 李大勇, 郭彦雪, 高玉峰, 等. 水平单调荷载作用下饱和细砂中裙式吸力基础土压力特性分析[J]． 土木工程学报, 2015，48(1):112-119．

[7] 李大勇, 曹立雪, 高 盟, 等. 水平荷载作用下裙式吸力基础承载性能研究[J]． 海洋工程, 2013，31(1):67-73．

[8] 李大勇, 冯凌云, 张雨坤,等. 饱和细砂中裙式吸力基础水平单调加载模型试验-承载力及变形分析[J]． 岩土工程学报, 2013，35(11):2030-2037．

[9] 王建华, 刘晶磊, 周扬锐. 静荷载与循环荷载作用下张紧式吸力锚承载特性的模型试验[J]． 岩土工程学报, 2012, 34(6):997-1004．

[10] Byrne B W. A Comparison of Field and Laboratory Tests of Caisson Foundations in Sand and Clay[J]． Géotechnique, 2006, 56(9)：617-626．

[11] 孟昭瑛, 梁子冀, 刘孟家. 浅海桶形基础平台水平承载力与抗滑稳定分析[J]． 海洋科学进展, 2000, 18(4):36-41．

[12] Obrzud R,Truty A.The Hardening Soil Model-a Practical Guidebook[M].Zace Services Ltd,Lausanne,Switzerland, 2011．

[13] 瞿小莉. 大直径圆筒结构土压力研究[D]．大连：大连理工大学, 2008．

[14] 许 英. 大直径薄壁圆筒结构土压力研究[D]．南京：河海大学, 2004．

[15] Prasad Y V S N, Chari T R. Lateral Capacity of Model Rigid Piles in Cohesionless Soils[J]． Soils & Foundations, 1999, 39(2):21-29．