多振子局域共振声子晶体导线带隙特性研究
2018-05-22王泽华张梦鸽
王泽华 张梦鸽 韩 林 张 研
(河海大学 力学与材料学院, 南京 210098)
0 引 言
导线舞动是一种复杂的由垂直力、水平力、扭转力共同作用的三维运动,属于空气动力学及柔性悬链结构的风力振动范畴[1].覆冰导线在风激励下会产生低频(0.1~3 Hz)、大振幅(导线直径的5~300倍)自激振动的现象[2-3].导线一旦发生大面积舞动,会导致线路频繁跳闸甚至断线倒塔事故,会造成大面积的停电,影响电网安全稳定运行.现今常用的控制导线舞动的方法是在线路上加防舞动装置[4],如防振锤、双摆防舞器等.防振锤实质上是一个动力减振器,能有效吸收导线的振动能量,减小线夹及导线的疲劳损伤;但防振锤线夹处很容易发生疲劳断股事故.双摆防舞器基于动力失稳条件所开发,若外界环境造成的失稳阈值大于设计条件,线路还将发生舞动现象,舞动振幅有时会较大.目前存在的各种防舞措施不能完全地解决导线的舞动问题,因此,关于导线防舞动措施及相应的技术方面需要进一步的研究.
声子晶体[5-8],又称弹性波带隙材料,因其弹性常数和密度呈周期性分布而展现出阻断特定频段弹性波传播的性质.声子晶体的带隙机理可分为Bragg散射型[9]和局域共振型[10].其中,Bragg机理强调弹性波与周期结构的相互作用,其带隙频率对应的波长与周期结构尺寸参数相当,若要产生频率越低的带隙就要构造尺寸越大的结构,这不利于声子晶体结构在低频范围的应用.而局域共振带隙[11]主要考虑单个散射体的共振特性,可以用小尺寸获得低频带隙.针对这一特性,考虑导线舞动的特点,局域共振型声子晶体的低频带隙特性具有用于导线防舞的巨大潜力.国内外学者针对声子晶体的带隙特性及机理已做了大量的研究工作,如声子晶体在梁[12]、杆[13]、薄板[14]、格栅[15]等结构的减振应用研究,已从各方面的研究中验证了其中振动带隙的存在.然而,声子晶体在导线结构上的应用还未见相关报道.
本文试图在已有的间隔棒的基础上,增设多个弹簧振子,将其周期排列在导线上,形成多振子声子晶体导线结构,探究其带隙特性.本文推导建立计算声子晶体导线结构振动频散关系的传递矩阵法.基于某舞动试验线路,计算其振动频散关系和带隙范围,并对相应的有限周期声子晶体导线进行振动传输特性分析以进行对比验证,为导线防舞技术提供理论支持.
1 基于传递矩阵法的声子晶体导线弹性波带隙计算
如图1所示,假定导线为张紧的细弦,受恒定张力和自重力作用,导线自重沿x轴方向均匀分布,单位长度质量为m(kg/m),导线的水平张力为T(N).导线振动的微分方程为
(1)
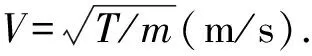
基于对式(1)的求解,可以得到导线振动的位移
y(x,t)=exp(iωt)[Acos(αx)+Bsin(αx)]
(2)
式中,α=ω/V,A和B为待定参数,可以通过边界常数确定.

图1 纯导线理论模型
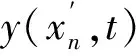
(3)
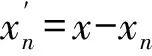
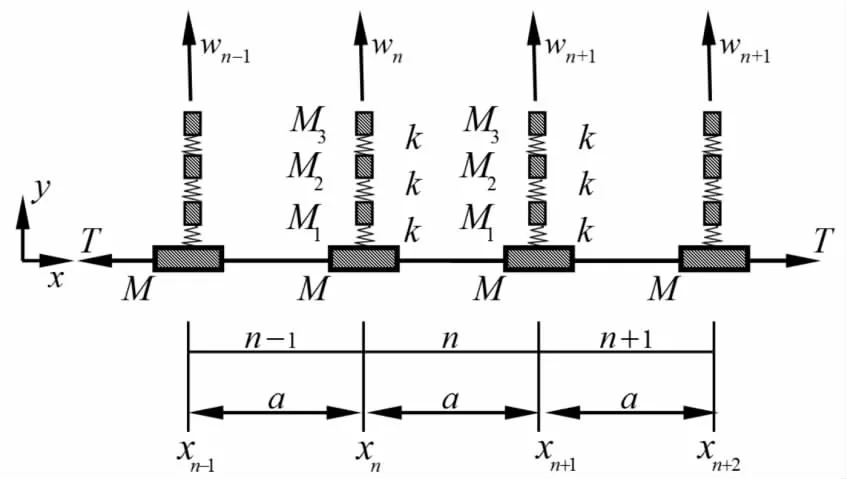
图2 串联多振子声子晶体导线理论模型
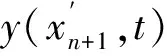
(4)
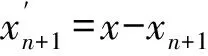
x=xn+1处间隔棒的位移即为导线在该处的位移.设x=xn+1处第j个振子(n+1)j的位移为
w(n+1)j=c(n+1)jexp(iωt)
(5)
式中,c(n+1)j为振子(n+1)j的振幅.
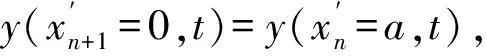
An+1=Ancos(αa)+Bnsin(αa)
(6)
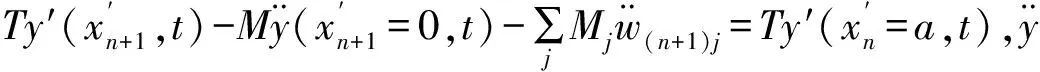
T[-Anαsin(αa)+Bnαcos(αa)]
(7)
同时考虑振子(n+1)j(j=1,2,3)的平衡,有
(8)
应用式(6)~(8)得到
KΨn+1=KΨn
(9)

由于x方向的周期性,利用Bloch定理[16],即
Ψn+1=exp(iqa)Ψn
(10)
式中,q为波数.
由式(9)和式(10),可以得到标准的矩阵特征值问题
|T-exp(iqa)I|=0
(11)
式中,T=K-1H;I为单位阵.T可以表示为
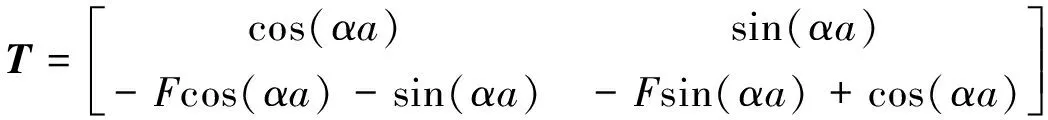
(12)
基于式(11),通过求解特征值问题,可以得到周期结构中圆频率ω与波数q之间的频散关系.在某些频率范围内,将无法求得与该范围内的频率相对应的实数q值,这些频率范围称作带隙.理论上在带隙的范围内导线不会发生舞动,进而能在实际中减弱导线的舞动幅度.
2 数值算例分析
某舞动试验线路长240 m,导线采用四分裂钢芯铝绞线,导线静态平均张力为16 kN,导线直径d=23.94 mm,截面积A=338.99 mm2.单位长度导线质量mc=1.133 kg/m.次档距为a=40 m.间隔棒质量M,振子质量M1、M2和M3,弹簧刚度系数k.取振子质量M1=1 kg,M2=1.5 kg,M3=2 kg,间隔棒质量M=2 kg,弹簧劲度系数k=10 N/m.计算研究可知,导线舞动是一种风致振动的低频高幅振动(0.1~3 Hz),取导线舞动频率范围0~0.9 Hz进行分析.
根据式(9)可以得到多振子声子晶体导线的带隙结构图,如图3所示.图3左图表示实波数与频率之间的关系,从图中看到,在0~0.9 Hz的频率范围下,存在3个带隙,带隙频率范围分别为:0.17~0.18 Hz,0.53~0.54 Hz,0.80~0.82 Hz.表明理论上在多振子声子晶体的作用下,导线在这3个频率范围内不会发生舞动.可以看到,存在的3个带隙频率处于低频范围,符合局域共振型声子晶体存在低频带隙的特性,并且局域型声子晶体导线带隙下边界由弹簧振子的弹簧刚度及各个振子质量决定,若改变其弹簧刚度及振子质量,可以得到不同的带隙频率范围.虚波数与频率的关系如图3所示.由于虚部不为零的波数对应着无法有效传播的衰减波,而波数虚部的模越大说明波衰减越强,因此,波数虚部模与频率的关系可以表示带隙内波衰减的性质.从图中可以看到,声子晶体导线存在波衰减的性质,并且波衰减的部分与频散关系相对应.
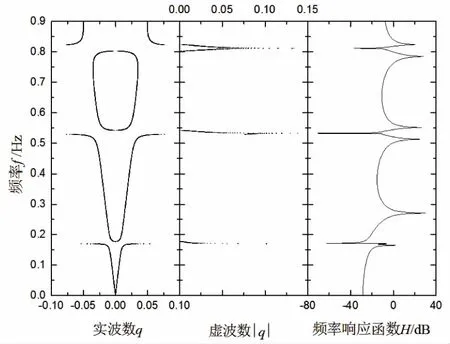
图3 声子晶体导线频散关系与频率响应函数曲线图
基于上述算例,即在240 m长导线上,等间距设置5个间隔棒弹簧振子.在有限元软件中建立有限周期声子晶体导线有限元模型.为便于简化分析,将模型简化为平面运动,故导线两端采用铰接约束,保证其在二维平面内振动.在导线一端施加简谐激励,另一端拾取响应,进行谐响应分析,输出响应的频谱与初始激励信号的频谱相比即可得到导线的振动传输特性,如图3右图所示.根据声子晶体的带隙特性,有限周期结构的幅频响应函数应在带隙频率范围对应的区域有大幅度下降,该下降程度表示传输的弹性波的衰减程度.图中在0~0.9 Hz内存在3个振动衰减区,衰减频率范围与图3中得到的无限周期条件下计算得到的带隙频率范围一致.有限元仿真结果与理论结果吻合较好,说明多振子声子晶体导线带隙确实存在,带隙的存在证实了周期在导线上排列的多个弹簧振子对导线的减振作用是有效的,能减弱导线的振动幅度.
3 结 论
本文采用传递矩阵法计算了无限周期一维串联多振子声子晶体导线的振动带隙,并通过有限元仿真对其有限周期结构的传输特性进行了研究,主要结论如下:
1)在纯导线微分振动方程的基础上,得到了多振子导线的振动方程;基于传递矩阵法,经过一系列的推导计算,得到多振子声子晶体导线的传递矩阵,进而得到多振子导线的频散关系.
2)经过计算分析,得到无限周期串联多振子声子晶体导线结构中存在振动带隙,并与其有限周期结构的振动传输特性相互对应,即表明在带隙频率范围内沿导线的振动传播会受到很大的衰减,导线舞动得到有效抑制.
3)具有局域共振特性的三串联多振子声子晶体导线具有3个低频带隙,带隙较为丰富.
总之,通过对多振子声子晶体导线的数值与仿真研究分析,获得并验证了该结构存在的带隙特性,这种声子晶体导线结构为导线防舞提供了新的思路.
参考文献:
[1] 韩 娟. 送电线路导线舞动分析[J]. 中国电力教育, 2013,29(11):218-229.
[2] 杨风利,杨靖波,付东杰,等. 输电线路导线舞动荷载分析[J]. 中国电机工程学报, 2011,31(16):102-107.
[3] 孙珍茂,楼文娟. 覆冰输电导线舞动及防舞效果分析[J]. 振动与冲击, 2010,29(5):141-146.
[4] 刘 瑞,刘耘成. 架空输电线路防舞动措施[J]. 东北电力技术, 2015,36(12):47-50.
[5] Chen J, Chan H L W, Cheng J. Large One-dimensional Band Gaps in Three-component Phononic Crystals Plates[J]. Physics Letters A, 2007, 366(4-5):493-496.
[6] Wu Z, Wang Y, Li F. Analysis on Band Gap Properties of Periodic Structures of Bar System Using the Spectral Element Method[J]. Waves in Random and Complex Media, 2013, 23(4):349-372.
[7] Zhen N, Wang Y, Zhang C. Bandgap Calculation of in-plane Waves in Nanoscale Phononic Crystals Taking Account of Surface/Interface Effects[J]. Physica E-Low-Dimensional Systems & Nanostructures, 2013, 54(8):125-132.
[8] Taniker S, Yilmaz C. Design, Analysis and Experimental Investigation of Three-dimensional Structures with Inertial Amplification Induced Vibration Stop Bands[J]. International Journal of Solids and Structures, 2015, 72(16):88-97.
[9] 温激鸿,韩小云,王 刚,等. 声子晶体研究概述[J]. 功能材料, 2003,34(4):364-367.
[10] Liu Z Y, Chan C T, Sheng P. Three-component elastic wave band-gap material[J]. Physical Review B, 2002, 65(16):165116.
[11] 文岐华,左曙光,魏 欢. 多振子梁弯曲振动中的局域共振带隙[J]. 物理学报, 2012,61(3):240-246.
[12] 郁殿龙,温激鸿,陈圣兵,等. 轴向载荷周期结构梁的弯曲振动带隙特性[J]. 振动与冲击, 2010,29(3):85-88.
[13] 郁殿龙,刘耀宗,王 刚,等. 一维杆状声子晶体振动中的表面局域态研究[J]. 机械工程学报, 2005,41(6):35-38.
[14] 吴 健,白晓春,肖 勇,等. 一种多频局域共振型声子晶体板的低频带隙与减振特性[J]. 物理学报, 2016,65(6):209-219.
[15] 温激鸿,郁殿龙,王 刚,等. 薄板状周期栅格结构中弹性波传播特性研究[J]. 物理学报, 2007,56(4):2298-2304.
[16] Shen M, Cao W. Acoustic bandgap formation in a periodic structure with multilayer unit cells[J]. Journal of Physics D:Applied Physics, 2000, 33(10):1150-1154.
