改进GM(1,1)模型在重力坝位移预测中的应用
2018-05-22祖安君黄显峰
祖安君 黄显峰
(河海大学 水利水电学院, 南京 210098)
水库大坝的安全对于国民经济来说非常重要,一旦大坝失事,将会产生严重后果.因此,对大坝进行安全监控,对监测资料进行建模分析尤为重要.常用建模方法有线性回归法,时间序列法等,这些方法均需有连续的长期观测资料,但我国很多大坝施工和蓄水期的监测资料有所欠缺,采用上述方法建模预测精度不高.而灰色系统理论专门针对“小样本、贫信息”进行建模分析[1],将大坝看作一个灰色系统,对监测得到的较少信息,通过累加、累减生成,逐步使灰色量白化,从而建立预测模型并做出预测[2],但基于这一理论的经典GM(1,1)模型在预测振荡序列方面有不足,预测精度亦不高.
在现代水利工程对大坝水平位移的监测中,位移数据序列时常呈现出非负随机振荡的趋势,为解决上述问题,本文使用改进GM(1,1)模型对非负振荡序列实施变换再进行预测,这一做法弥补了经典GM(1,1)模型在预测振荡序列方面的缺陷,有效提高了预测精度.运用该模型与经典GM(1,1)模型、线性回归模型对某大坝水平位移预测进行对比,结果也印证这一点.
目前,国内外对改进GM(1,1)模型的研究基本和粮食、人口等预测有关,工程方面涉及较少,因此本文所提改进方法在目前同行业相关问题的研究中有一定借鉴意义.
1 经典GM(1,1)模型的建模机理
设某原始数据序列为:
X0={x(0)(1),x(0)(2),…,x(0)(n)}
(1)
其中:x(0)(k),k=1,2,…,n.
对该序列进行一次累加(1-AGO)生成,得到序列为:
X1={x(1)(1),x(1)(2),…,x(1)(n)}
(2)
X1的紧邻均值生成序列为:
Z(1)={z(1)(2),z(1)(3),…,z(1)(n)}
(3)
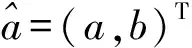
Y={x(0)(2),x(0)(3),…,x(0)(n)}T
(4)
则GM(1,1)灰色微分方程(又称为灰色方程的差分形式)为:
x(0)(k)=az(1)(k)=b
(5)
此时由最小二乘法得到的估计参数列满足:
(6)
白化微分方程为
(7)
原始序列的模拟预测差分形式为:
(x(0)(1)-b/a)(e-a-1)e-a(k-1)
(8)
在该模型中,a为发展系数,b为灰色作用量.
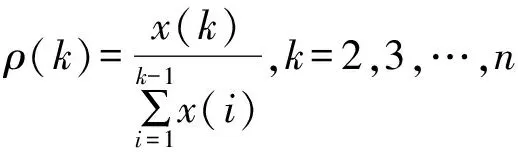
对非指数增长序列和振荡序列,可以考虑微分、差分混合形态的EGM,即经典GM(1,1)模型[4],但该模型也暴露出一些问题.经典GM(1,1)模型对单调的序列适用性很强,应用于其他变化趋势时拟合精度不高[5],而工程中经常遇到非负振荡序列.另外,由于很多工程中的监测序列都不满足光滑离散条件[6],因此经典的GM(1,1)预测方法存在一定的缺陷,需要改进.
2 改进GM(1,1)模型建模机理及方法
2.1 建模机理
对于非负随机振荡序列的建模,关键问题是选择适当的序列变换方法从而生成新序列.钱吴永使用加速平移生成和加权平均生成操作改进光滑度然后建立了一个随机振荡序列的预测模型[7].本文通过类比改进提出了一种把原始非负随机振荡序列通过加速指数变换和几何平均生成变换转换为单调增长序列的方法,然后对变换后的序列建立经典GM(1,1)模型进行预测,再把序列还原,即为改进GM(1,1)模型的建模过程.
2.2 加速指数变换和几何平均生成变换
设X={x(1),x(2),…,x(n)}为原数据序列,则:
1)若∃k,k′∈{1,2,…,n-1},有x(k)
M=max{x(k)|k∈{1,2,…,n}},
m=min{x(k)|k∈{1,2,…,n}}
(9)
M-m是序列X的振幅.
定义加速指数变换.设X={x(1),x(2),…,x(n)}是原数据序列,满足:x(k)>0,k=1,2,…,n,记T=M/m,且有以下定义:
M=max{x(k)|k∈{1,2,…,n}},
m=min{x(k)|k∈{1,2,…,n}}
它的变换序列为XE1=(x(1)e1,x(2)e1,…,x(n)e1),式中:
x(k)e1=x(k)Tk-1,k=1,2,…,n
(10)
称E1为加速指数变换.通过简单数学推导可证明非负随机振荡序列经过加速指数变换后得到的序列为单调增长序列.
再定义几何平均生成变换.设X={x(1),x(2),…,x(n)}是原数据序列,满足:x(k)>0,k=1,2,…,n.称变换
(11)
是几何平均生成变换,记为E2.同样,容易证明几何平均生成变换不改变原数据序列的单调性,即当原数据为单调增长序列时,变换后的数据序列仍然单调递增.
2.3 改进后的GM(1,1)模型对随机振荡序列的建模
设原始数据序列Y={y(1),y(2),…,y(n)}为随机振荡序列,其中y(k)>0,k=1,2,…,n.
那么建立模型的过程如下:
1)对原数据序列Y进行加速指数变换,得
Y′={y′(1),y′(2),…,y′(n)}
(12)
2)对序列Y′采用几何平均生成变换,得
X0={x(0)(1),x(0)(2),…,x(0)(n)}
(13)
3)对序列X0进行一次累加生成,得
X1={x(1)(1),x(1)(2),…,x(1)(n)}
(14)
4)建立GM(1,1)模型的白化微分方程:
(15)
其中a和b是该模型的待估参数.
5)GM(1,1)模型的灰色微分方程为:
y(k)+az(1)(k)=b
(16)
式中,背景值的定义和经典GM(1,1)模型中的定义相同,即:
(17)
6)式(17)的解即GM(1,1)模型的时间响应序列为:
(18)
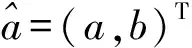
(19)
式中:
Y={x(0)(2),x(0)(3),…,x(0)(n)}T
(20)
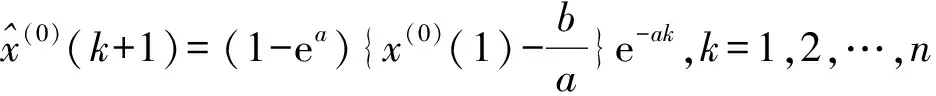
7)还原序列

式中:
(21)
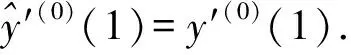
在此基础上进一步对数据进行还原得:
k=2,3,…,n
(22)
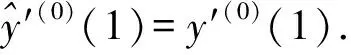
改进的GM(1,1)模型适用于小样本非负随机振荡序列的建模与预测.对小样本非负随机振荡序列进行加速指数变换和几何平均生成变换,若所得新序列的光滑比为递减序列,则新序列满足经典GM(1,1)模型的光滑离散条件,这时可用改进GM(1,1)模型对原样本进行建模.因此在应用改进GM(1,1)模型进行预测时需先对原序列进行数据变换,再判断其是否在模型的适用范围内.
3 工程实例及分析
3.1 工程概况
某水库是一座以灌溉为主,兼有防洪、生态综合效益的中型水库.水库大坝为浆砌石重力坝,大坝总长274 m,其中主坝长144 m,最大坝高52 m,底宽58 m,顶宽6 m,坝顶高程1 037.62 m,水库的另外组成部分还有溢洪道和放水隧洞.
3.2 重力坝Y向水平位移预测
该水库的重力坝自建成后,安排专门人员对坝顶上下游方向和左右岸方向的水平位移进行观测,并进行了监测数据的记录.受天气、监测仪器精度等条件影响,获取的监测数据不完整.现取2015年5月29日至6月10日这连续13 d的坝顶Y向(左右岸方向)水平位移监测数据进行分析.取前8 d的数据进行建模,然后根据相应模型进行后5 d数据的预测.以下分别采用改进GM(1,1)模型、经典GM(1,1)模型和传统线性回归模型对监测数据进行建模和预测.
3.2.1 改进GM(1,1)模型对坝顶水平位移的预测
用改进GM(1,1)模型对坝顶水平位移进行拟合与预测,由于原序列是非负随机振荡序列,不严格满足光滑离散条件,且不是递增序列,故使用前文所说的加速指数变换和几何平均生成变换对序列进行变换.变换后序列的光滑比分别为:1.288,0.803,0.594,0.528,0.444,0.440,0.418,该序列为递减序列,即变换后的序列严格满足光滑离散条件,由2.3节改进GM(1,1)模型的适用范围知,改进GM(1,1)模型适用于该工程2015年5月29日至6月10日连续13天的水平位移监测序列.于是用前8 d的数据进行建模,后5 d的数据进行预测.由式(12)~(22)可得用改进的GM(1,1)模型得到的拟合值和预测值及其相对误差见表1.
3.2.2 经典GM(1,1)模型对坝顶水平位移的预测
先对原数据序列进行光滑性检验,由于原序列的光滑比分别为:0.885,0.563,0.300,0.294,0.137,0.225,0.139.由此可见,该序列在第6个测值处光滑比出现增大的情况,随后第7、8两个测值处又呈现减小趋势,即总体上光滑比随序号的增大而减小,可认为其满足光滑离散条件.
该水平位移序列属于典型的振荡序列,综合考虑由于光滑比只在一个点处不满足要求,随后又呈现递减的趋势,因此可以采用经典GM(1,1)模型用前8 d的数据进行建模,随后由式(1)~(8)可以得到时间响应序列的预测公式,然后对后5 d的数据进行预测.用经典GM(1,1)模型得到的拟合值和预测值及其相对误差见表1.
3.2.3 传统线性回归模型对坝顶水平位移的预测
线性回归模型是用于解决数理统计问题中变量之间关系的常规模型,它是利用线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的回归分析,自变量和因变量均为一个时称为一元线性回归.回归系数通常用经典的最小二乘法进行求解.本文采用以日期为自变量、水平位移为因变量的一元线性回归模型对所选连续8 d的水平位移测值进行建模,得到的拟合值和预测值及其相对误差见表1.

表1 3种方法拟合与预测情况对比
3.3 结果分析
从表1可以看出,改进GM(1,1)模型、经典GM(1,1)模型及线性回归模型的拟合值平均误差分别为13.45、14.07、14.80,预测值平均误差分别为10.62、22.04、18.46.传统线性回归模型对随机振荡序列的拟合及预测精度均不高,而经典GM(1,1)模型对该大坝水平位移拟合值的平均误差较线性回归降低了0.73%,降低不到1%,但预测值和线性回归法的结果相比,平均误差提高了3.58%.究其原因,该工程2015年5月29日至6月10日连续13 d的序列属于非负随机振荡序列,在对前8 d的水平位移测值建模时,经典GM(1,1)模型没有严格满足光滑离散条件,因而预测值不理想.而改进GM(1,1)模型弥补了经典GM(1,1)模型的缺陷,不仅对该序列的拟合精度有所提高,更使预测值平均误差较线性回归模型和经典GM(1,1)模型降低了一倍,有效提高了预测精度.
通过工程实例应用可以看出,改进GM(1,1)模型使用了两个数据序列的变换技巧,使原先的非负随机振荡序列通过变换成为单调增长序列,提高了原始序列铁光滑度[8],从而让变换后的序列能够满足经典GM(1,1)模型的离散条件,进而能够迅速精确地建立模型,弥补了经典GM(1,1)模型的缺陷.同时具有建模简单、操作方便、计算简洁的优点,它可以定义较少的参数,所有参数均可准确快速求得,因此可以减少由于不断调整参数和试算而导致的不必要的错误,也避免了大量的复杂计算与推导.此外,该改进方法不失一般性,对于水利工程上具有非负随机振荡特点的效应量小样本序列的建模及预测均适用,在水利工程大坝效应量的预测方面能够起到较好的效果,发挥比较重要的作用.
经典GM(1,1)模型可以实现根据小样本序列建模,其对单调序列预测效果较好,但对工程中的很多非负振荡序列并不能实现精度高的预测.而传统线性回归模型适用范围局限于呈线性变换规律的序列,对非负振荡序列的预测精度较低.
4 结 论
1)通过工程实例,将传统线性回归模型、经典GM(1,1)模型和基于序列变换的改进GM(1,1)模型对非负随机振荡序列的预测结果进行对比,说明了改进GM(1,1)模型在对非负随机振荡序列的预测中弥补了经典GM(1,1)模型的缺陷.
2)结果表明改进GM(1,1)模型建模简单、计算简明,且预测精度显著提高,并有较强实用性.
参考文献:
[1] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[2] 陈孝珍,马中军.GM(1,1)灰色模型在某大坝水平位移预测中的应用[J].水利与建筑工程学报,2006,4(3):22-24.
[3] 王 勇,胡 平,申 莲.GM(1,1)改进模型在大坝位移预测中的应用[J].云南水力发电,2010,27(2):28-30.
[4] 刘思峰,曾 波,刘解放.GM(1,1)模型的几种基本形式及其适用范围研究[J].系统工程与电子技术,2014,36(3):501-506.
[5] 郑雪琴,秦 栋.系统优化的GM(1,1)模型在大坝位移预测中的应用[J].水电能源科学,2011,29(4):76-77.
[6] 王 洁,王 波.上海未来短期客运量的预测分析-基于最小二乘法改进的GM(1,1)模型[J].数学的实践与认识,2017,47(13):67-73.
[7] Xiao Xinping, Hu Yichen, Guo Huan. Modeling Mechanism and Extension of GM(1,1)[J].Journey of Systems Engineering and Electronics,2013,24(3):445-453.
[8] 潘 勇,吴小丽,李 科.基于改进加权灰色GM(1,1)模型的高速公路交通量预测[J].公路交通技术,2016,32(6):131-134.
