利用兰姆波检测混凝土板的材料特性

各种混凝土结构的超声波检测工作已经得到了充分的开展,其中应用较多的超声波是纵波和声表面波分析[1-4]。但是由于纵波在混凝土构件中来回反射且混凝土材料的粘滞性、内部空隙和裂纹等影响,探测精度无法有效保证[5]。同时由于声表面波在混凝土结构表面传播,振动能量主要集中于1.5个波长以内,其探测深度非常有限[6]。

兰姆波是一种在弹性板中传播的板波,最早由H. Lamb研究并命名[7]。由于兰姆波有传播距离长、多模态可选和检测范围广等优点,在板状结构的无损检测和传感器技术领域都得到了广泛的应用[8]。朱哲民等分析了各种负载情况下薄板中兰姆波的传播[9-10]。庄杰等利用兰姆波对铝合金疲劳损伤进行了检测[11]。孙明清等通过将PZT压电陶瓷片直接粘贴在混凝土表面来激发和接收弹性波信号并确定了兰姆波的检测模态[12]。然而这些工作都没有给出混凝土结构中兰姆波检测模态的选取依据和方法。本文建立了兰姆波在混凝土板中传播的波速方程,探讨了混凝土板兰姆波检测的模态选取和动弹性模量的推定等问题。

1 方程推导

兰姆波在半无限大混凝土板中的传播见图1。发射端利用正压电效应产生振动,弹性波通过混凝土板内部后被接收端获取信号,最后利用获得的兰姆波信息来推定混凝土板的特性[12]。在严格控制骨料尺寸的情况下,可以认为混凝土板是各向同性材料[12]。这里我们忽略热传导,亥姆赫兹方程可以表示为[8]

(1)

式中:φ,ψ,kL和kT分别是混凝土板中纵波和横波的速度势函数和波矢量。波矢量定义如下

kL=ω/cL,kT=ω/cT

(2)

式中:ω为兰姆波的角频率,cL和cT分别为混凝土板的纵波和横波波速,其定义如下

(3)

式中:λ,μ和ρ分别为混凝土材料的拉梅常数和密度。

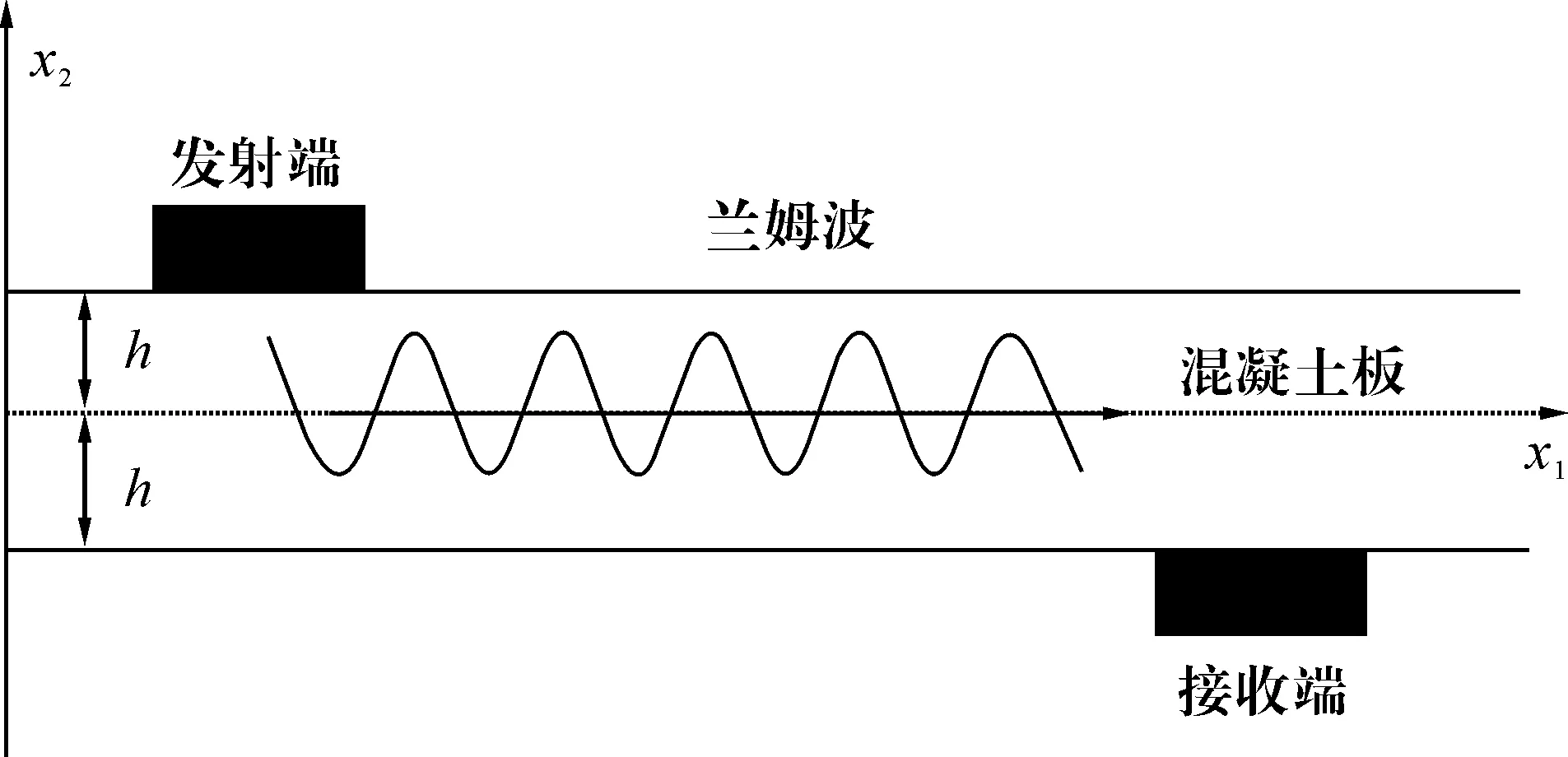
图1 混凝土板中兰姆波传播示意图

如图1所示,兰姆波沿x1方向传播,其声波势函数的形式解可以表示为[9]

φ=[Acosh(qx2)+Bsinh(qx2)]ei(ωt-kx1),

ψ=[Csinh(sx2)+Dcosh(sx2)]ei(ωt-kx1)

(4)

式中:A,B,C,D和k分别为待定常数和兰姆波的波矢量,q和s为新定义的符号,具体形式如下

(5)

混凝土板中的切向应力和法向应力分别为[9]

(6)

兰姆波在如图1所示的混凝土板中传播时,必须满足上下端面的自由边界条件如下

T2(x2=h)=T6(x2=h)=0,

T2(x2=-h)=T6(x2=-h)=0

(7)

将形式解(4)代入应力表达式(6)最终代入边界条件式(7),可以得到关于A,B,C,D的4个线性方程组,此方程组有非零解的充要条件是其系数矩阵的行列式值为零,也就是

det|M|=0

(8)

式中矩阵M的元素如下

m11=(-λk2+λq2+2μq2)cosh(qh),

m12=(-λk2+λq2+2μq2)sinh(qh),

m13=-2μikscosh(sh),m14=-2μikssinh(sh),

m21=-2μikqsinh(qh),m22=-2μikqcosh(qh),

m23=-μ(k2+s2)sinh(sh),

m24=-μ(k2+s2)cosh(sh),

m31=(-λk2+λq2+2μq2)cosh(-qh),

m32=(-λk2+λq2+2μq2)sinh(-qh),

m33=-2μikscosh(-sh),

m34=-2μikssinh(-sh),

m41=-2μikqsinh(-qh),

m42=-2μikqcosh(-qh),

m43=-μ(k2+s2)sinh(-sh),

m44=-μ(k2+s2)cosh(-sh)

(9)

在给定混凝土弹性模量、密度和泊松比以及板厚情况下,可以对波速方程(8)进行数值求解获得兰姆波波速,从而建立兰姆波特性(波速)和混凝土弹性模量之间的关系。整个计算过程可以利用Matlab程序进行求解。

2 数值计算

实验研究表明只要限定超声波频率在160 kHz以下,且严格控制混凝土骨料的尺寸,这样激发的兰姆波波长比骨料尺寸大,可以将实验制备的混凝土板视为均质和各向同性材料[12]。混凝土板的材料参数如下

E=52.56 GPa,ν=0.2,ρ=2 480 kg/m3

(10)

式中:E和ν分别为混凝土材料的弹性模量和泊松比。获得的混凝土板中兰姆波的色散曲线见图2。

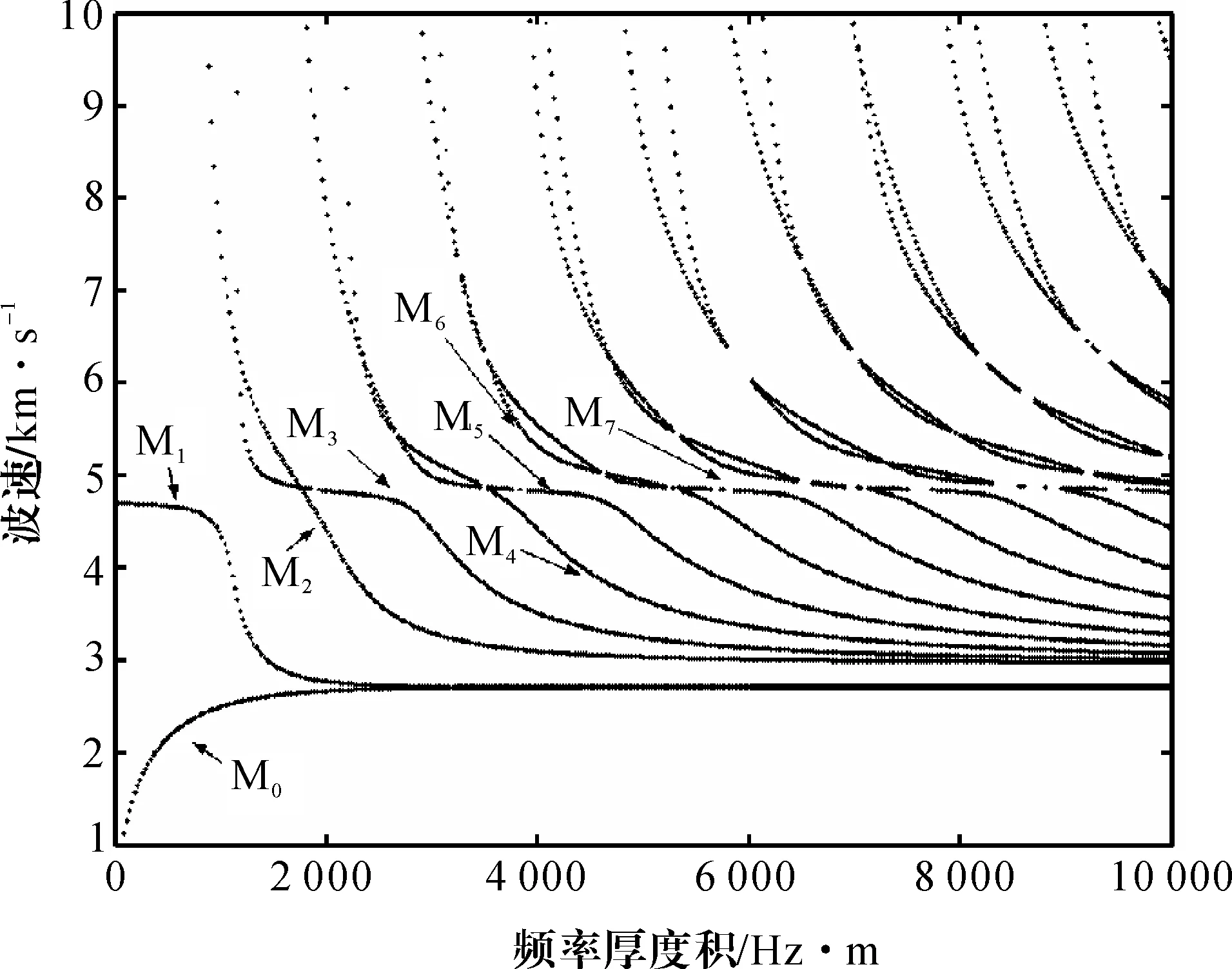
图2 混凝土板中兰姆波的色散关系

从图2中可以发现，随着频率的升高,混凝土板中将会依次出现M0,M1,M2,M3等一系列的模态,这为混凝土板的兰姆波检测提供了多种模态的选择。与金属板中兰姆波的色散曲线相比,混凝土板中兰姆波各种振动模态的挤压和跳变将更加明显,这也为混凝土板兰姆波检测模态的选取增加了难度[9,12]。王骥等通过选取石英晶体板的最佳长厚比来避免石英晶体谐振器高频振动时各种模态的强烈耦合[13-15]。基于这一思想,可以通过判断混凝土板中兰姆波各振动模态的耦合情况来选取最佳检测模态。实验结果表明当发射信号频率为150 kHz时能有效激发混凝土板中的兰姆波[12],获得该激发频率下兰姆波波速和板厚的关系曲线见图3。

图3 混凝土板中兰姆波波速和板厚关系 (f=150 kHz)

同样，在图3中可以观察到多个兰姆波波速的存在。当混凝土板厚增加时,我们发现这些振动模态的挤压将更加严重。例如M0和M1模态,也就是第一组对称和反对称模态,在混凝土板厚达到100 mm时,这两个波速的相差值在0.01 m/s以下,几乎无法区分。同样当混凝土板厚为100 mm时,M6和M7模态能与其他模态清晰区分,实验中就是利用这两组检测模态作为超声波检测的工作模态[12]。

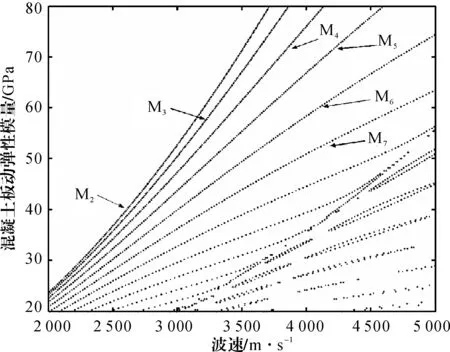
图4 混凝土板中兰姆波波速与动弹性模量的关系(f=150 kHz, 2h=100 mm)

在给定激发频率和板厚的情况下,我们获得了混凝土板中兰姆波波速与动弹性模量的关系，见图4。这里需要指出的是在图4中并没有给出M0和M1模态的曲线,通常这两种模态一般不作为检测模态[12]。图4表明随着混凝土动弹性模量的不断增加,各种模态的波速也在增加,其中有些模态的近似线性的关系提供了检测和推定的可能。在实际检测中,只要给定混凝土板厚并能有效激发兰姆波,就可以通过选择检测模态和测定波速来推定混凝土的动弹性模量。

3 结 语

本文研究了兰姆波在混凝土板中的传播特性。根据色散关系图中兰姆波各振动模态的耦合情况来选取最佳工作模态。接着提出了利用兰姆波来检测混凝土板动弹性模量的方法。数值计算结果表明我们选取的兰姆波工作模态正是实验中采用的检测模态。我们发现随着混凝土板厚度的增加,所获得的兰姆波各模态的挤压将更加明显。同时随着混凝土动弹性模量的增加,各模态的波速都在增加,其中有些模态几乎线性的关系提供了检测和推定的可能。

参 考 文 献

[1] 赵治广. 超声波检测非金属材料的研究与开发[J]. 实验技术与管理, 2006, 23(10): 30-32.

[2] 张春雨, 杨春雷. 钢管混凝土缺陷超声波定量检测技术初步研究[J]. 公路交通技术, 2012(2):67-70.

[3] Song W S. Nondestructive evaluation techniques using impact-generated stress waves in concrete[D]. Illionis: Northwestern University, 2001.

[4] 曲华, 宁建国, 李学慧. 利用瑞利波频谱分析法无损检测混凝土结构[J]. 混凝土, 2006(2): 76-80.

[5] 张建仁, 黄浩, 彭辉, 等. 用纵波换能器测量混凝土横波波速及动弹性模量的实验研究[J]. 中外公路, 2011, 31(3): 89-92.

[6] 吴荣兴, 袁丽莉. 温度效应对声表面波传播的影响[J]. 压电与声光, 2013, 35(1): 10-15.

[7] Rose J L. Ultrasonic waves in solid media[M]. Cambridge: Cambridge University, 1999．

[8] Auld B A. Acoustic fields and wave in solids[M]. Malabar, Florida: Krieger Publishing Company, 1995．

[9] Zhu Z M, Wu J R. The propagation of lamb waves in a plate boarded with a viscous liquid[J]. Journal of the Acoustical Society of America, 1995, 98(2): 1507-1064．

[10] Zhu Z M, Wu J R, Li J, et al. A general dispersion relation of Lamb wave sensors with liquid-layer loading[J]. Sensors and Actuators A Physical, 1995,49:79-84．

[11] 庄杰, 林宇, 黄炜, 等. 基于Lamb波群速度的铝合金疲劳损伤检测[J]. 压电与声光, 2014, 36(4): 648-653.

[12] 孙明清, Staszewski W J, Swamy R N. 混凝土中的Lamb波传播[J]. Journal of Wuhan University of Technology, 2004, 26(1): 31-34.

[13] Wang J, Zhao W H. The determination of the optimal length of crystal blanks in quartz crystal resonators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2005, 52(11):2023-2030．

[14] Wu R X, Wang J, Huang D J, et al. The nonlinear thickness-shear vibrations of quartz crystal plates under an electric field[J]. International Journal of Nonlinear Mechanics, 2014, 61:32-38.

[15] Ma T F, Wu R X, Wang J, et al. Coupled extension and thickness-twist vibrations of lateral field excited AT-cut quartz plates[J]. Acta Mechanics Sinica, 2014, 30(1): 67-72．