基于Udwadia-Kalaba理论的自动离合器位置跟踪控制∗

张 琰，赵 韩，黄 康，姜建满

(1.合肥工业大学机械工程学院，合肥 230009； 2.安徽江淮汽车集团股份有限公司，合肥 230009)

前言

对于具有相互约束的复杂机械系统如何进行动力学的建模是分析动力学研究领域的重点和难点之一。自Lagrange建立分析力学以来，众多的数学家和物理学家在这一领域都做出了重要的贡献。如Maggi方程、Boltzmann-Hamel方程、Gibbs-Appell方程、Udwadia-Kalaba方程等，但以上大多数研究中都是基于达朗贝尔(d’Alembert)原理和虚位移原理。针对约束系统，可以利用拉格朗日(Lagrange)乘子进行约束力的有效计算，但在实际应用中有一定的困难，尤其是针对复杂的多自由度机械系统。文献[1]～文献[4]中提出了Udwadia-Kalaba方程，此方法可在不出现Lagrange乘子的条件下，相对简单地求出完整约束和非完整约束状态下的系统运动方程，并给出解析解，成为分析动力学领域里的一项重大突破。

基于Udwadia-Kalaba方程的约束控制是目前伺服约束控制中较为前沿的研究方向之一。Udwadia首先应用伺服约束的控制方法对非线性机械系统的轨迹进行跟踪控制，并进行了初步的研究[5]。与传统的非线性机械系统的控制相比，该伺服控制的方法在不增加运算的基础上，实现了对机械系统轨迹的精确跟踪控制。利用Udwadia等的研究成果，文献[6]～文献[10]中较为详细地提出了机械系统伺服约束控制的概念和如何利用伺服控制来实现约束力的设计。在利用Udwadia-Kalaba方程对不确定系统的自适应鲁棒控制方面，文献[11]～文献[13]中也进行了深入研究。文献[14]中在Udwadia-Kalaba方程基础之上，对完整和非完整约束状态下非线性机械系统的控制进行了深入地研究，并提出一种状态反馈控制器。

针对离合器位置跟踪控制，目前已有很多先进的控制方法，文献[15]和文献[16]中提出了反馈线性化的方法，将非线性问题转化为线性控制问题，再根据线性控制理论进行控制器的设计。但是该方法是建立在系统的数学模型基础之上，当系统的参数发生变化后，该方法的控制效果将变差。文献[17]和文献[18]中给出了滑模变结构的控制方法，根据系统状态偏离滑模切换面的程度来切换控制器的控制参数或结构，进而使系统按照切换面确定的规律运动，该控制具有较好的鲁棒性。但实际系统中存在着惯性、固定空间滞后和状态测量误差，这些现象会导致高频抖振的发生，这种抖振将会使离合器的跟踪控制效果变差[19-20]。由于离合器在起步、换挡时的接合时间很短(大约0.7～2s)，采用较复杂的控制方法在短时间内完成系统的辨识和矫正不太合适，因此必须采用简单且鲁棒性较好的控制算法。

本文中将离合器的接合规律视为系统的约束，用伺服控制的方式来施加约束力，并利用Udwadia-Kalaba方程来分析求解约束力。建立电流-位置双闭环控制系统来实现离合器位置的精确跟踪控制，通过试验与传统的控制方法对比控制效果。

1 约束机械系统的动力学模型

1.1 约束机械系统

对于某机械系统，取状态变量的广义坐标表述为q＝[q1，q2，…，qn]T，其系统动能为

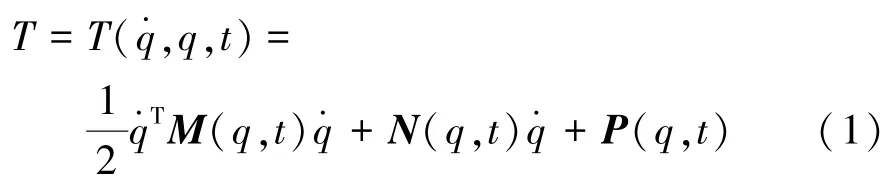
式中：M(q，t)＝MT(q，t)为n×n维对称且正定的质量矩阵；N(q，t) ∈R1×n且P(q，t) ∈R。

该系统不受外界约束时，其运动方程为

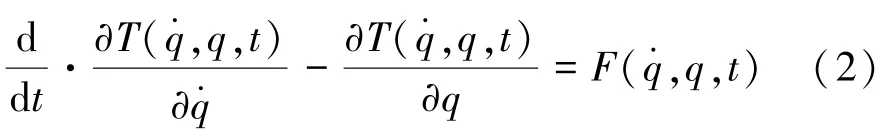
将式(1)代入式(2)得非约束系统的运动方程为

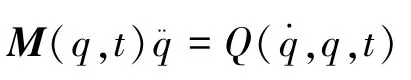
其中

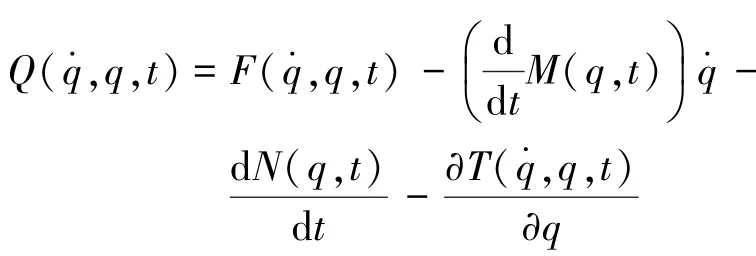
此处，可视为该非约束机械系统所受的合外力。

假设该机械系统受到一组约束：

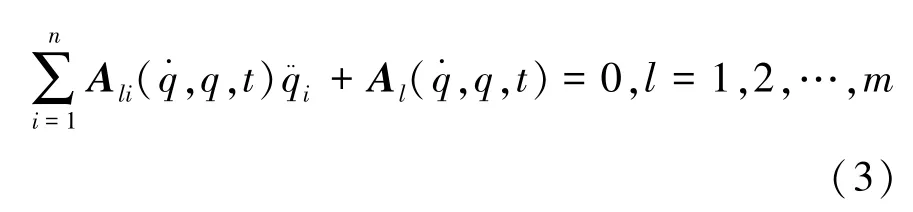
式中：A li(q，t)和A l(q，t)都为n×1维列矩阵，式中表示的约束可以是完整约束、非完整约束、定常约束和非定常约束等。式(3)的Pfaffian形式为

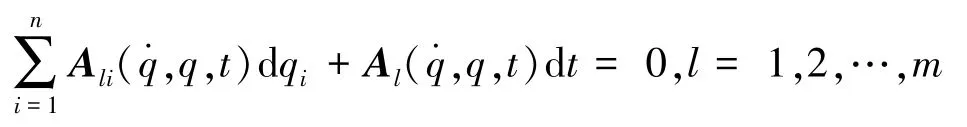
假设虚位移为δq∈Rn，则

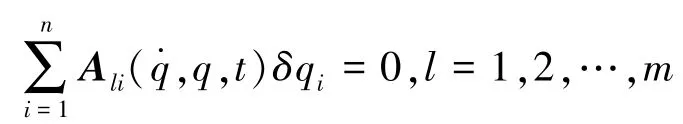
上述约束写成矩阵的形式为

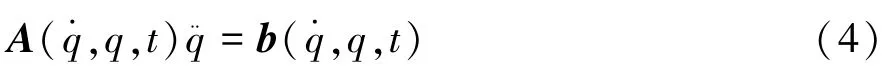
其中：A＝[A li]m×n；b＝[b1b2…bm]T

该“约束机械系统”的动力学方程为

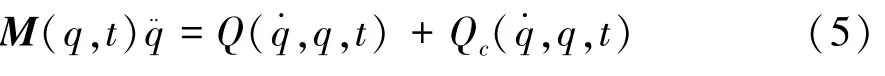
式中：可视为由外加约束所造成的约束力。

拉格朗日力学中，用Lagrange乘子表述约束时最常见的系统建模法。该法中，约束力表述为

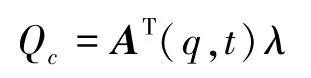
式中λ∈Rm为Lagrange乘子。因而式(5)可表述为

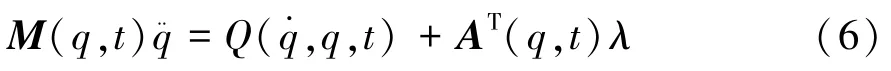
式(3)和式(6)联立可解出系统的广义加速度q¨∈Rm和Lagrange乘子λ∈Rn，但这些解一般不能以解析解的形式给出。因此，Lagrange的建模方法不能用于通用的系统特性分析(如稳定性和收敛性等)和控制系统的设计[4]。

1.2 Udwadia-Kalaba理论

假设在约束条件式(4)下，有一组n维向量v为系统某瞬时位移，则

Av＝0

令v＝M-1/2u，B＝AM-1/2则有

Bu＝0

式中：u为n维非零向量，B为约束矩阵。

令为n维列矩阵，由式(4)计算得

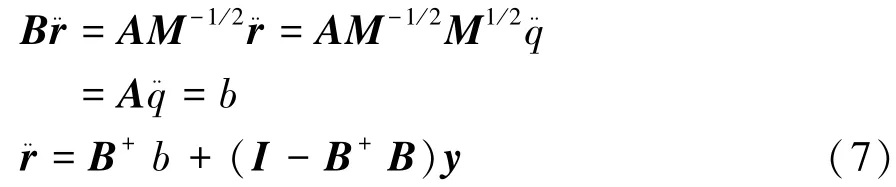
式中：y为任意n维向量；I为单位矩阵。

由于约束力在虚位移上所做的功之和为零，则

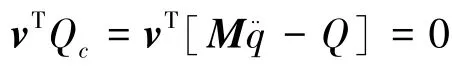
由以上定义，

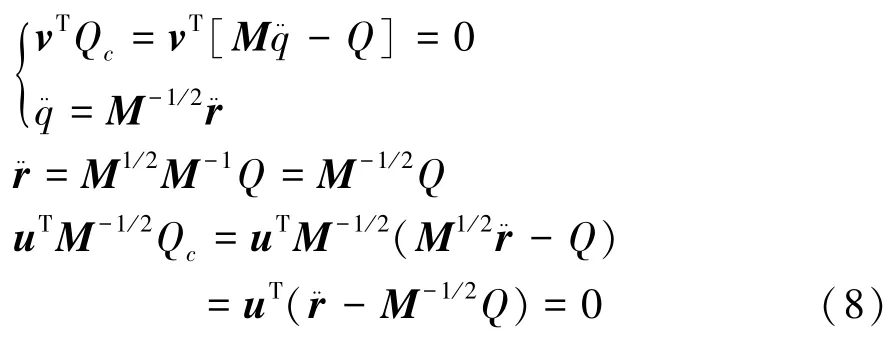
将式(7)带入式(8)得

因为Bu＝0，uTBT＝0，根据Moore-Penrose广义逆矩阵的性质可知，uTB+＝0，故式(9)可简化为

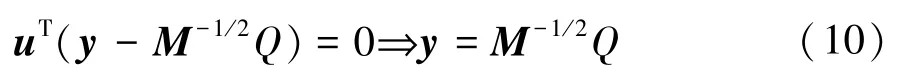
将式(10)代入式(7)得

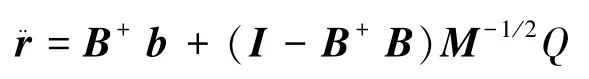
由定义得

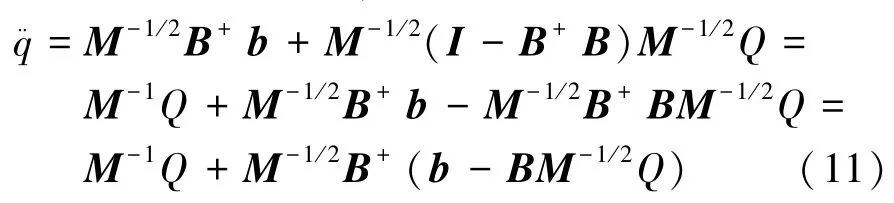
将上式两边同时乘以M，并代入B＝AM-1/2得

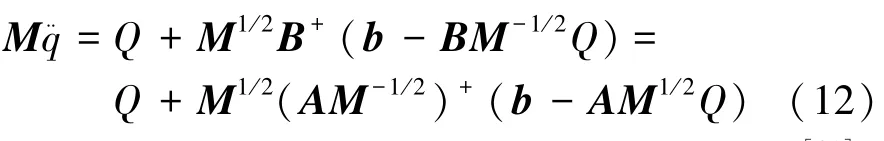
式(12)被称为Udwadia-Kalaba动力学方程[21]，于是，受约束机械系统所受约束力为

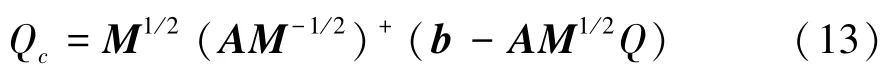
2 离合器位置跟踪控制

2.1 离合器接合过程的动力学模型

离合器及其执行机构的简图如图1所示。其中，膜片弹簧简化成杠杆、弹簧和阻尼系统。膜片弹簧小端连接分离轴承，其小端位移λ2等于分离轴承的轴向位移，膜片弹簧大端连接压盘，其大端位移λ1等于压盘的轴向位移。

图2为膜片弹簧的载荷-变形特性曲线。由离合器接合过程和膜片弹簧工作状态分析可知，离合器的接合可以分为以下3个阶段。

(1)空行程阶段

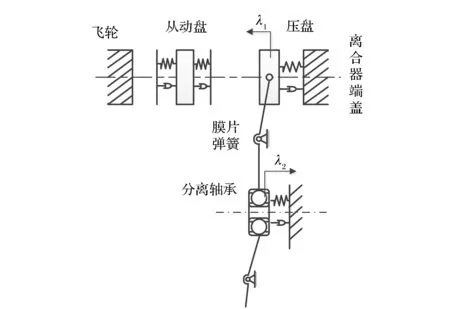
图1 离合器及其执行机构结构简图

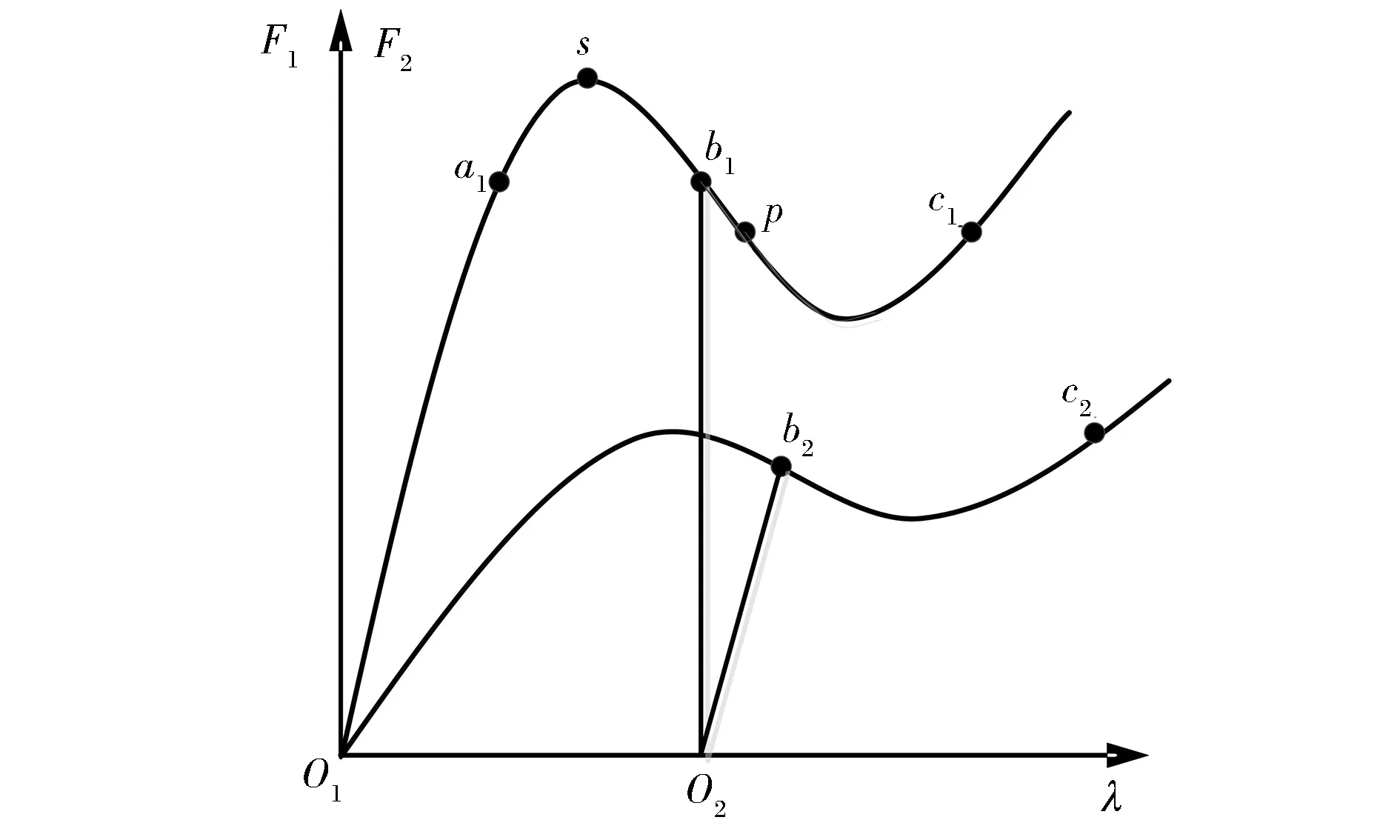
图2 膜片弹簧的载荷 变形特性

从分离状态到接合开始时，膜片弹簧小端处于最大位移处，分离指小端施加的载荷F2从最大值开始逐渐减小，此时，膜片大端尚未与压盘接触，膜片弹簧大端载荷F1＝0，即空行程阶段。此时，膜片弹簧特性取F2＝f(λ2f)特性阶段的c2b2，即分离轴承小端的载荷位移关系为

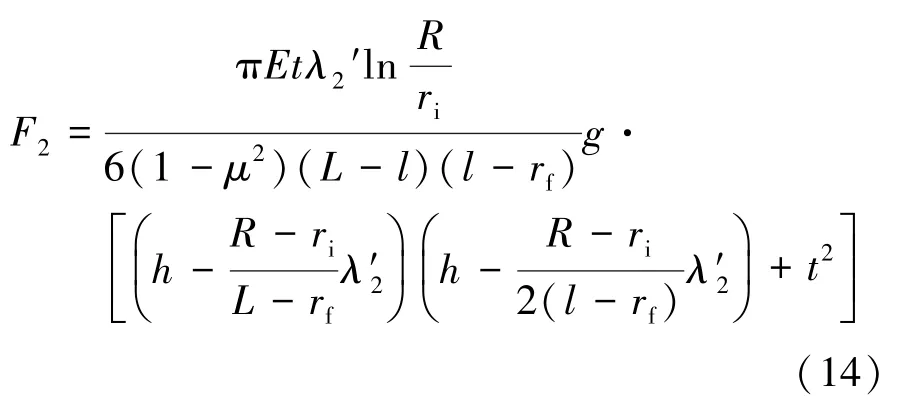
式中：R为膜片弹簧外径；ri为膜片弹簧内半径；rf为膜片弹簧承载半径；r0为膜片弹簧小端半径；L为膜片弹簧外承载半径；l为膜片弹簧内承载半径；E为膜片弹簧弹性模量；μ为膜片弹簧泊松比；h为膜片弹簧内锥高；t为膜片弹簧板厚。

(2)滑摩阶段

随着膜片弹簧小端位移的减小，大端碟簧部分开始接触压盘，由于碟簧部分为刚性，因此大端的变形量保持不变。大端与压盘之间的载荷F1从零开始增大(大端载荷特性曲线为O2b1段)，直到离合器从动盘与飞轮转速同步。同时，分离指小端施加的载荷F2继续减小，由膜片弹簧特性分析可知，该阶段小端载荷线性减小至零(小端特性曲线为b2O2段)，即分离轴承小端的载荷位移关系为

其中

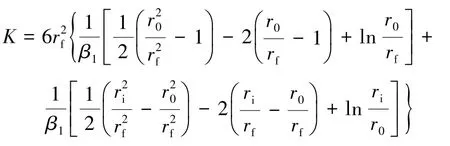
(3)同步阶段

从离合器从动盘与飞轮同步开始，至离合器传递转矩不再增长为同步阶段，离合器大端恢复至预压紧状态(点a1)。大端载荷变化为b1a1段，小端在该阶段没有载荷。

分离轴承的受力分析如图3所示，拨叉对分离轴承的轴向压力为Qc，即理想的约束力，膜片弹簧对分离轴承的轴向压力为F′2，跟膜片弹簧小端的轴向载荷F2为作用力和反作用力，即无外在约束(理想控制力)时，由于弹性恢复力，膜片弹簧仍能够恢复到初始状态，其载荷和变形关系为式(14)。分离轴承的运动方程为

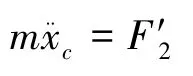
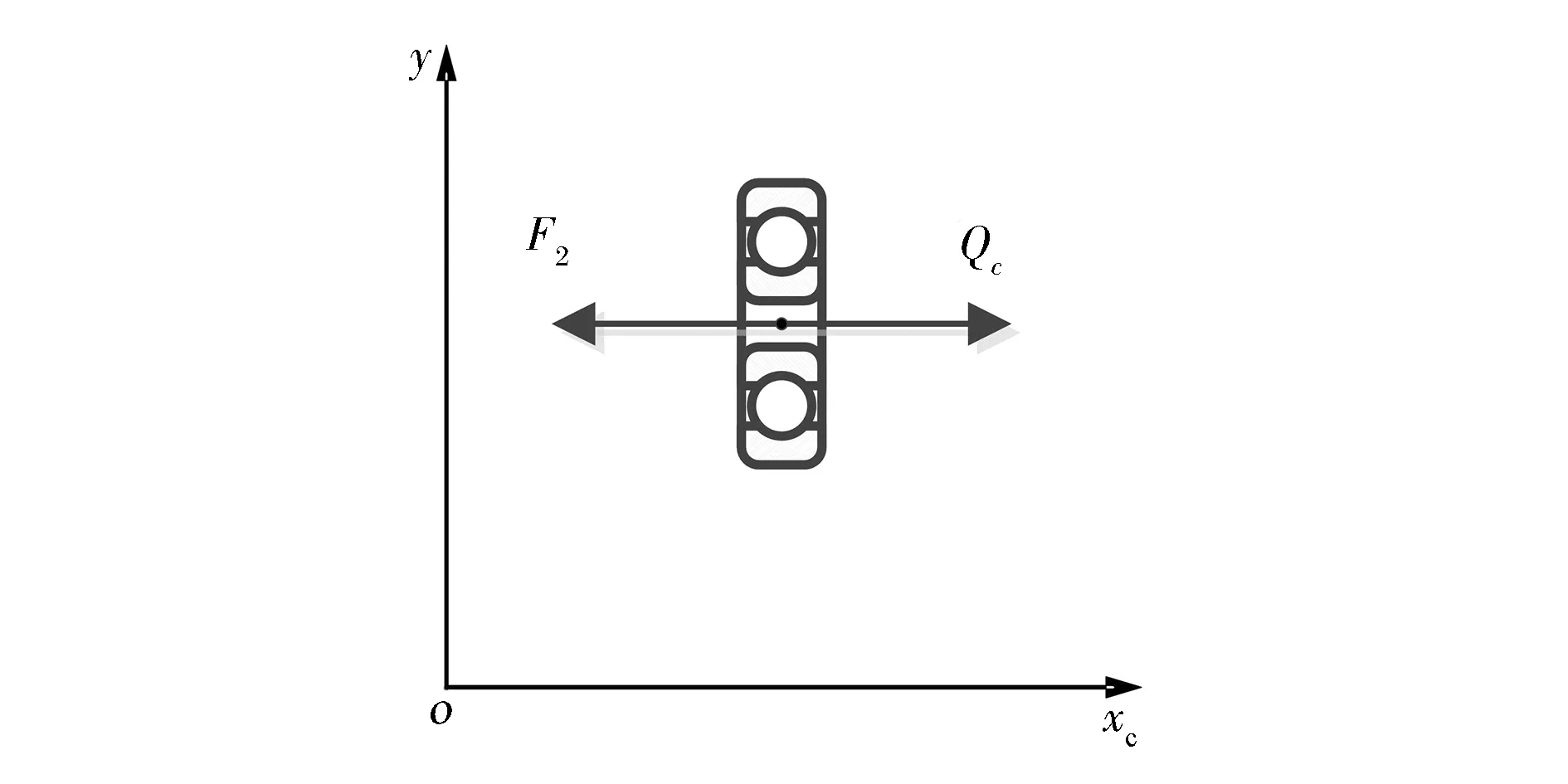
图3 分离轴承受力分析

2.2 Udwadia-Kalaba理论在离合器位置控制中的应用

离合器执行机构的原理框图如图4所示。速度环需要使用光电编码器，由于汽车机舱的工作环境比较恶劣，光电编码器对环境要求较高，考虑成本和可靠性等因素，本文中只使用电流-位置双闭环控制系统。电流控制器采用PID控制，输出为电机PWM值。位置控制器采用上节阐述的Udwadia-Kalaba控制方法。

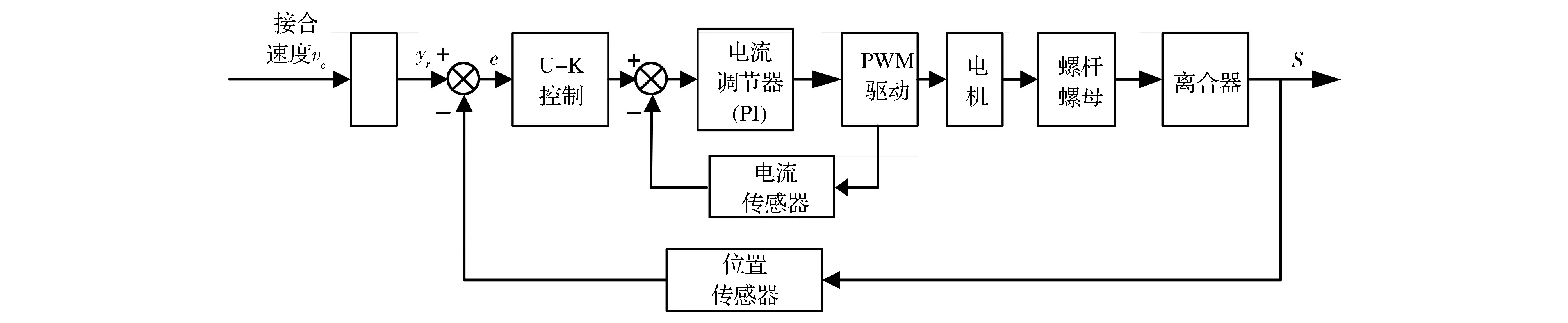
图4 自动离合器位置跟踪控制原理图

将相关参数代入式(5)得

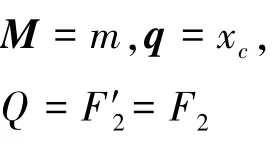
空行程阶段：

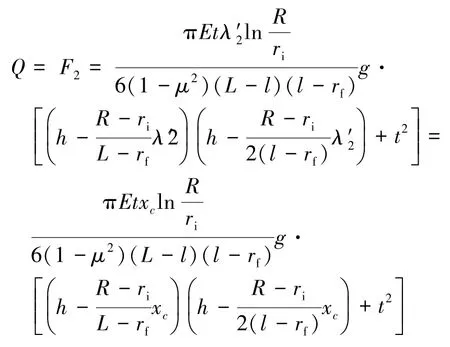
滑摩阶段：

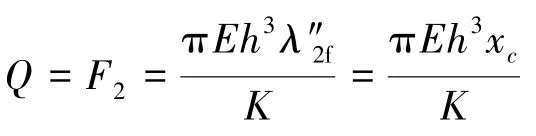
分离轴承的约束为文献[21]中离合器的接合规律，将该控制规律进行最小二乘法曲线拟合：

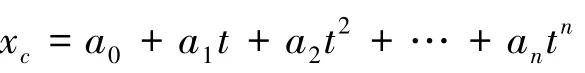
对上式约束求时间的2阶导数，并代入式(4)得

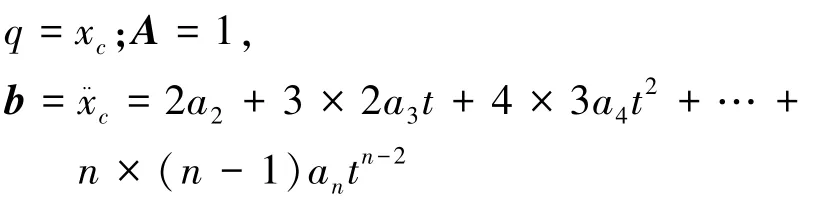
根据式(12)，该分离轴承的运动方程为

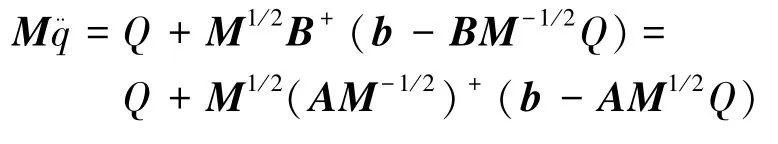
代入以上各参数，对空行程阶段和滑摩阶段分别进行详细解析。

3 离合器跟踪控制试验

本文中研究的自动离合器执行机构采用电磁阀—液压式如图5所示，它结构简单，控制精度高，空间布置方便，主要由液压泵、高速开关阀等部件组成。它利用PWM信号控制高速开关阀的通断时刻，直接控制离合器工作油缸的充放油速度，从而实现离合器的分离和接合。由图5可知，离合器接合位置为分离轴承的轴向位移，即膜片弹簧小端的轴向位移xc＝λ2。位移传感器检测分离油缸内活塞的实时位移xp，经分离拨叉机构的几何关系可折合到分离轴承处的轴向位移，即满足关系式xp＝f(xc)。

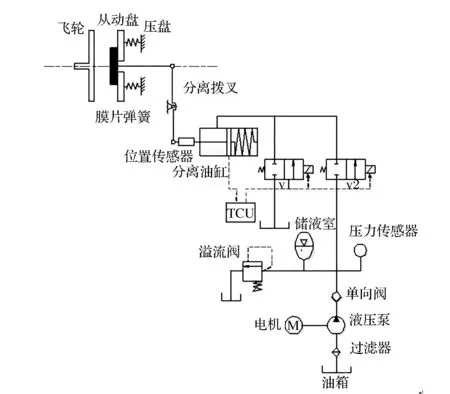
图5 自动离合器执行机构的工作原理图

3.1 台架试验

离合器位置跟踪控制试验在AMT试验台架上进行，离合器当前接合位置由位置传感器进行检测。目前采用较多的是“快—慢—快”的离合器接合规律[22]，如图6所示。AB段为空行程阶段，此时没有转矩的传递，为减少动力中断时间，减小冲击感，应尽快接合离合器；BC段为滑摩阶段，该阶段应调整离合器的接合速度，不宜过快以满足换挡舒适性，又不宜过慢以免增大离合器的磨损；CD段为同步阶段，为缩短换挡时间应以最大接合速度接合离合器。

本文中采用马瑞利某款离合器，后备系数为1.5，平均压力为0.3MPa，摩擦片外径为250mm，内径为155mm，厚度为3.5mm。本文中采取的A/D转换器的分辨率为10bit，离合器的总行程为45mm。AMT试验台架如图7所示，主要由AMT控制系统和试验设备构成，试验设备主要有电动机、转矩仪、AMT系统(带有离合器总成)、增速器、换向器、电涡流测功机和惯性飞轮组。

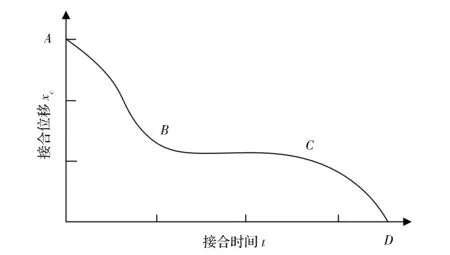
图6 自动离合器的接合规律曲线

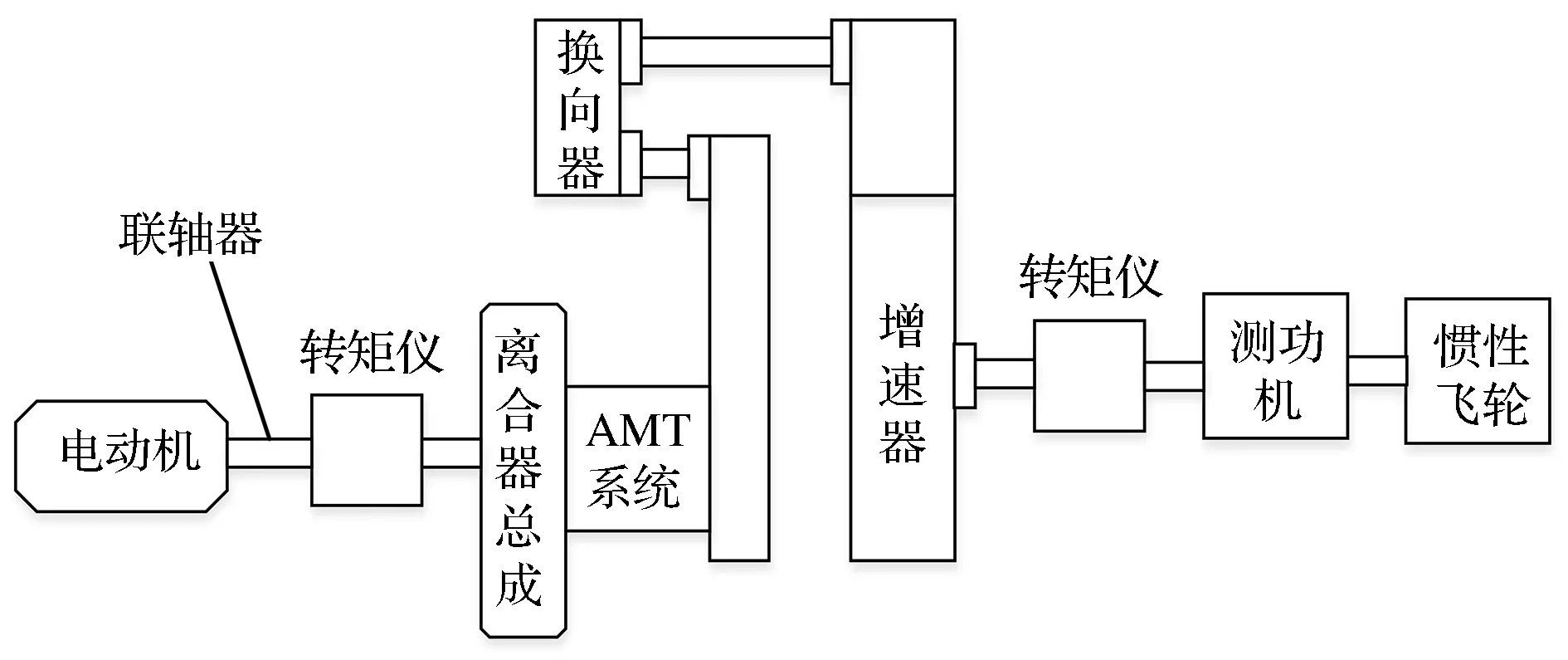
图7 AMT试验台架布置示意

车辆行驶过程中受到各种阻力，经过换算求出变速器输出轴上的阻力矩，由试验台架通过电涡流测功机对增速器的输出轴进行加载来模拟。在给定试验工况下，经换算求出测功机上的加载转矩

Tdm(t)为

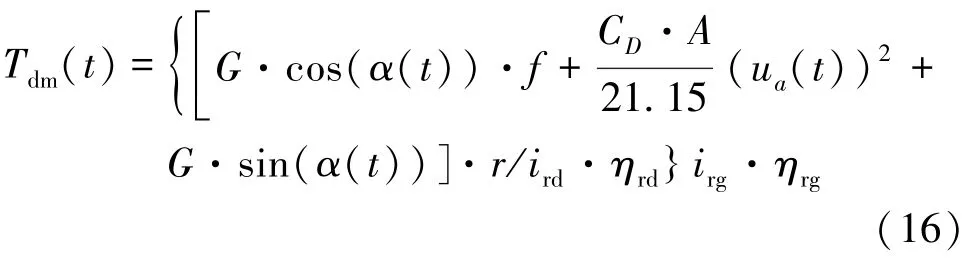
式中：ird为变速器输出轴到车轮的传动比；irg为台架试验上变速器输出轴到测功机的传动比；ηrd为变速器输出轴到车轮的传动效率；ηrg为台架试验上变速器输出轴到测功机的传动效率。

车辆的加速阻力在台架试验上通过对惯性飞轮组加载来模拟，包括平移质量和旋转质量两部分，由于旋转质量系数较难获得，因此，此处采取能量等效的原理，将平移质量换算成转动惯量，惯性飞轮组的转动惯量Jrg为

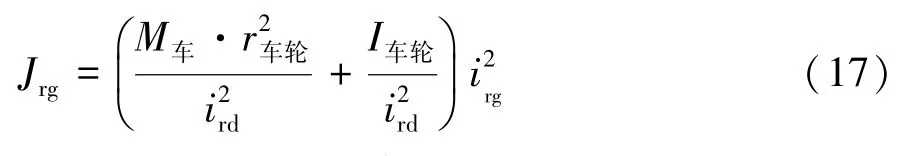
式中：M车为整车质量为车轮半径；I车轮为所有车轮转动惯量的总和。

在试验台上模拟车辆在平直的干燥沥青路面上缩短均匀加速，实际操作为节气门开度均匀变化，在换挡过程中节气门关闭。根据以上行驶工况，节气门开度的变化率反映了驾驶员的操作意图，电涡流测功机根据式(16)模拟道路情况，惯性飞轮组根据式(17)来模拟加速阻力。根据节气门开度和道路负载对试验台控制系统进行初始化，通过调节节气门开度的变化和电涡流测功机的励磁电流来达到不同的控制要求，试验参数如表1所示。

表1 台架试验参数

为验证本文中提出的基于Udwadia-Kalaba理论的离合器位置跟踪控制性能，分别进行了基于Udwadia-Kalaba理论的控制和常规PID控制的试验。通过对比，取2挡升3挡的部分离合器位置跟踪试验曲线结果图进行说明。图8(a)和图8(b)为采取常规PID控制的离合器位置跟踪结果曲线，图8(c)和图8(d)为采取U-K控制的离合器位置跟踪结果曲线。

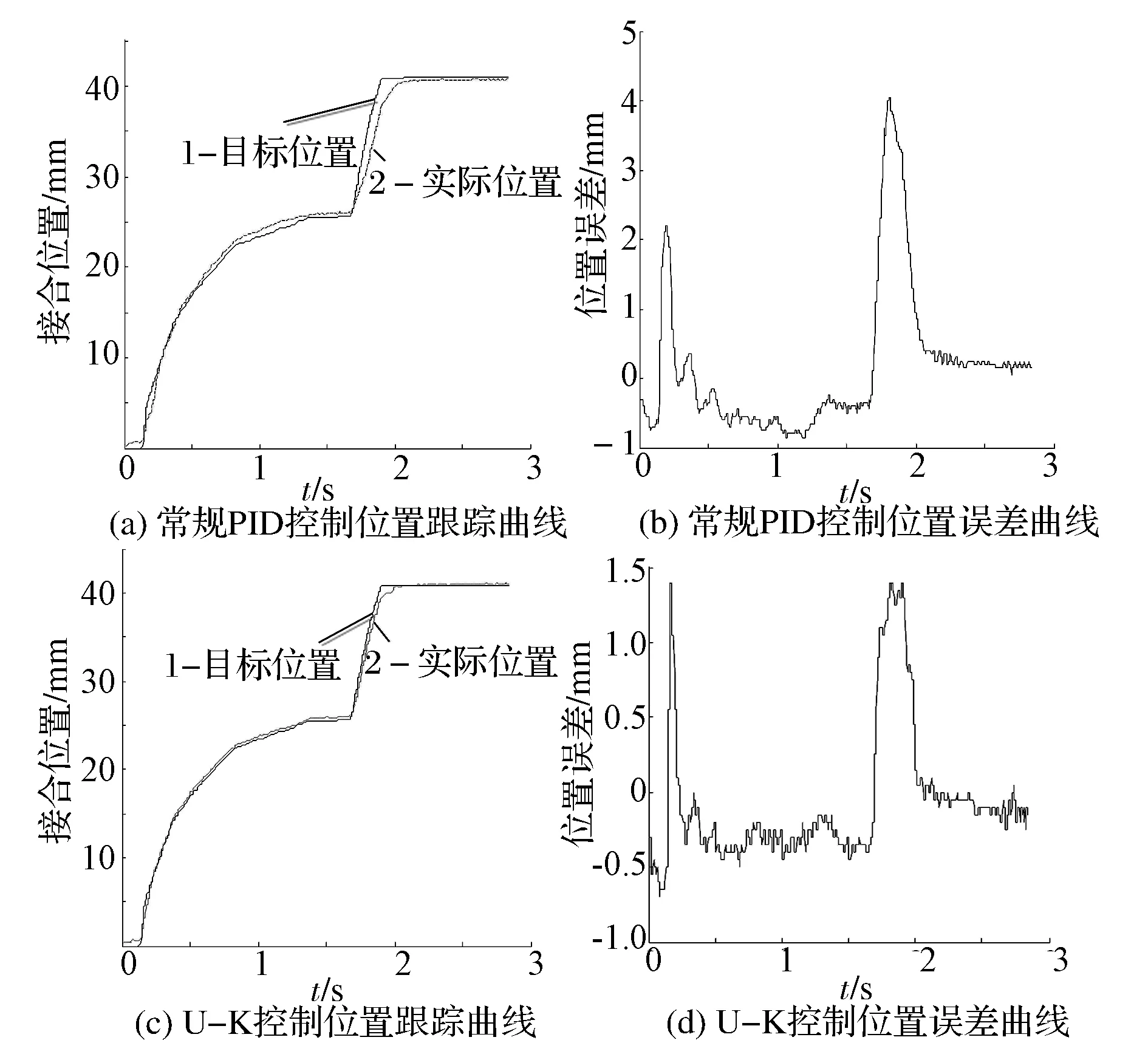
图8 常规PID控制和U-K控制离合器位置跟踪曲线和误差

图8(a)和图8(c)中的曲线1表示离合器目标接合位置曲线，曲线2表示不同控制策略下离合器的实际接合位置曲线。由图可见，常规PID控制下，离合器接合过程反应较慢出现比较严重的滞后和超调，大的超调意味着更大的接合速度，导致车辆在换挡过程中出现较大的冲击，使离合器磨损加剧，寿命缩短。通过对比误差曲线，可以明显看出，U-K控制方法的跟踪误差最大值比常规PID控制的最大误差减小62.5%左右，且振荡幅度明显减小，显示出优越的动态控制性能。从图中还可以看出，最大误差出现在速度改变最大时，这是由于系统惯性引起的，无法消除，只能通过一定的手段来减小。

3.2 实车试验

为进一步验证本文中提出的离合器跟踪控制方法的效果，在实车上分别进行了不同挡位的升挡和降挡试验，图9为试验样车系统框架图，表2为AMT试验样车的主要参数表。

图9 试验样车系统框架图

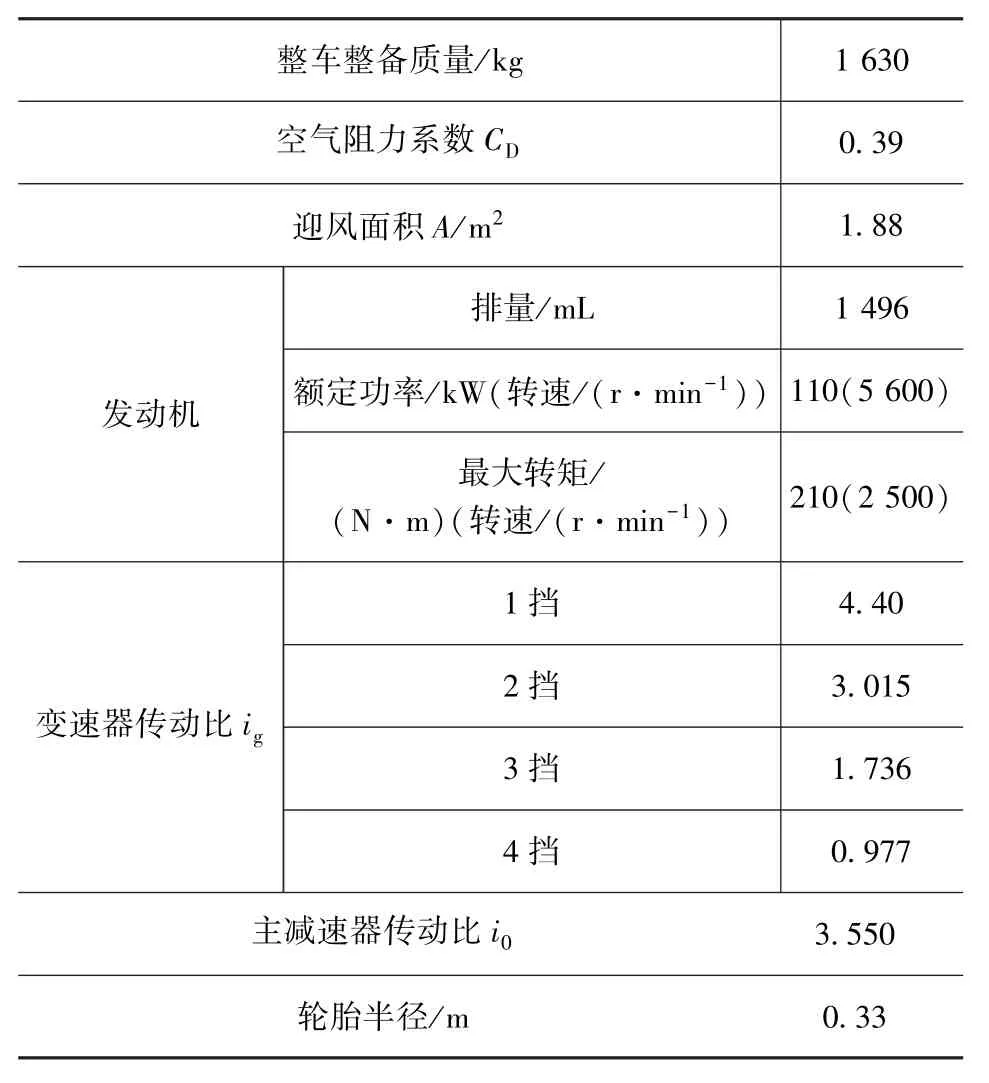
表2 AMT试验样车主要参数

在良好的沥青路面进行整车换挡试验，原地起步，逐渐从1挡连续换挡至5挡，然后松开加速踏板，逐渐从5挡降至1挡。在换挡试验过程中，当车辆达到换挡车速时，节气门开度迅速减小至零，离合器开始分离，离合器控制系统发出退挡、选挡和换挡的控制指令给执行机构，操纵执行机构进行相应动作，然后离合器进行接合，同时节气门开度根据TCU的控制策略逐渐恢复至目标开度，完成换挡过程。图10(a)和图10(b)分别示出了1挡升2挡的仿真和实车试验的对比结果，实车试验位置跟踪误差的最大值为1.22mm，而仿真的位置跟踪误差的最大值为0.85mm。试验时由于存在诸多的外界干扰，加上所建模型也存在一定的简化，使仿真结果与试验结果存在一定的偏差，但从图中曲线可以看出两种结果基本吻合，进一步验证了本文中所设计的离合器接合位置跟踪控制方法的可行性。图11和图12分别为升挡和降挡过程离合器位置跟踪和误差曲线。

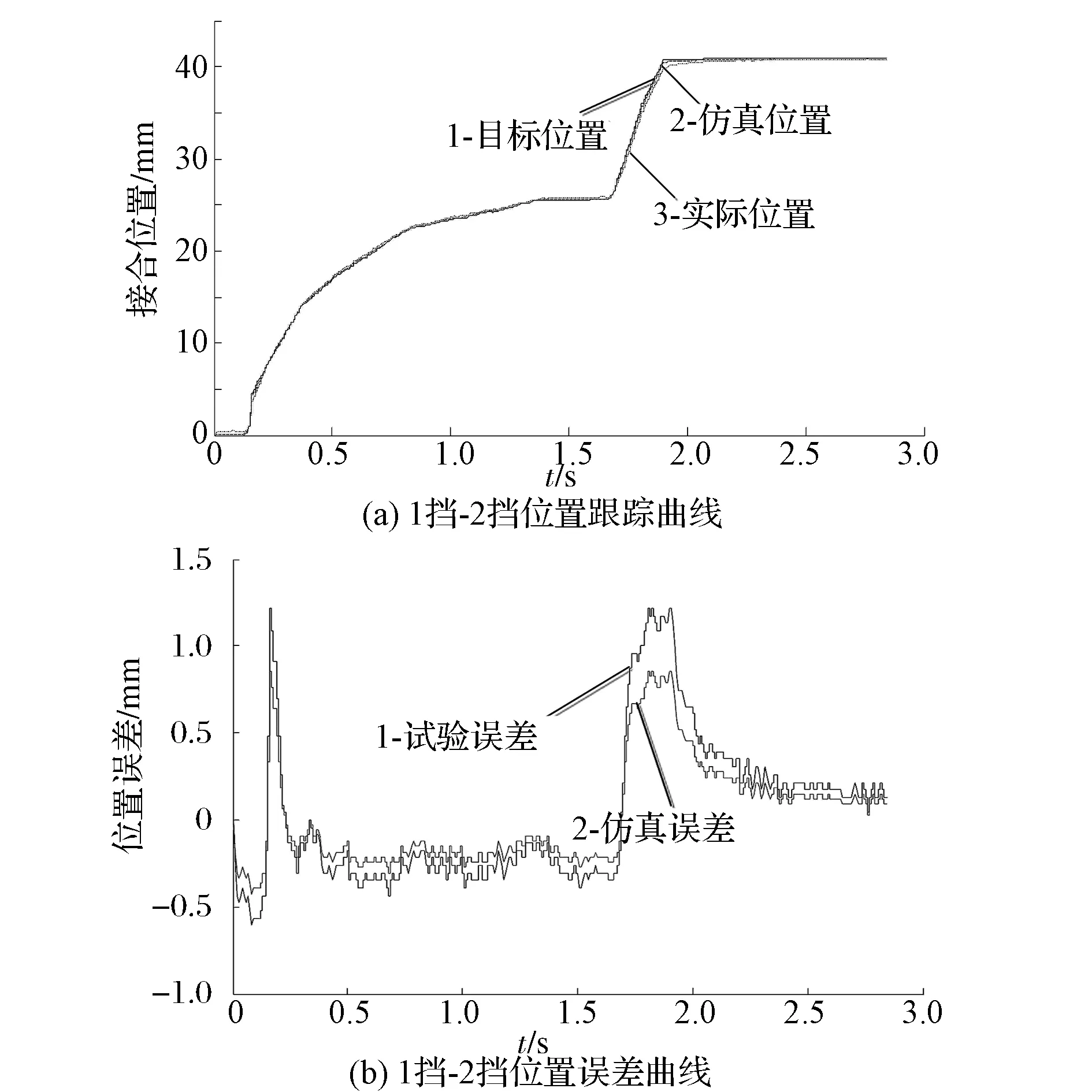
图10 1挡-2挡试验对比曲线

由图11可见，离合器位置跟踪误差最大值分别为1.71，1.65和1.95mm，离合器最大行程为45mm，故位置误差百分比为3.8%，3.67%和4.33%，满足一般跟踪误差在5%以内的精度要求。由图12可见，离合器位置跟踪误差最大值分别为2.08，2.15和2.14mm，位置误差百分比分别为4.62%，4.78%和4.76%，也都满足误差在5%以内的精度要求。可以看出，本文中提出的关于离合器位置跟踪控制的Udwadia-Kalaba方法在实车试验上得到了较好的验证。在换挡试验中，由于系统存在惯性，离合器位置跟踪有一定的滞后，误差最大值出现在速度改变方向的时段。升挡和降挡过程中，离合器的实际位置都能较好地跟踪目标位置，说明基于U-K理论的跟踪控制系统具有较好的自适应性和鲁棒性。

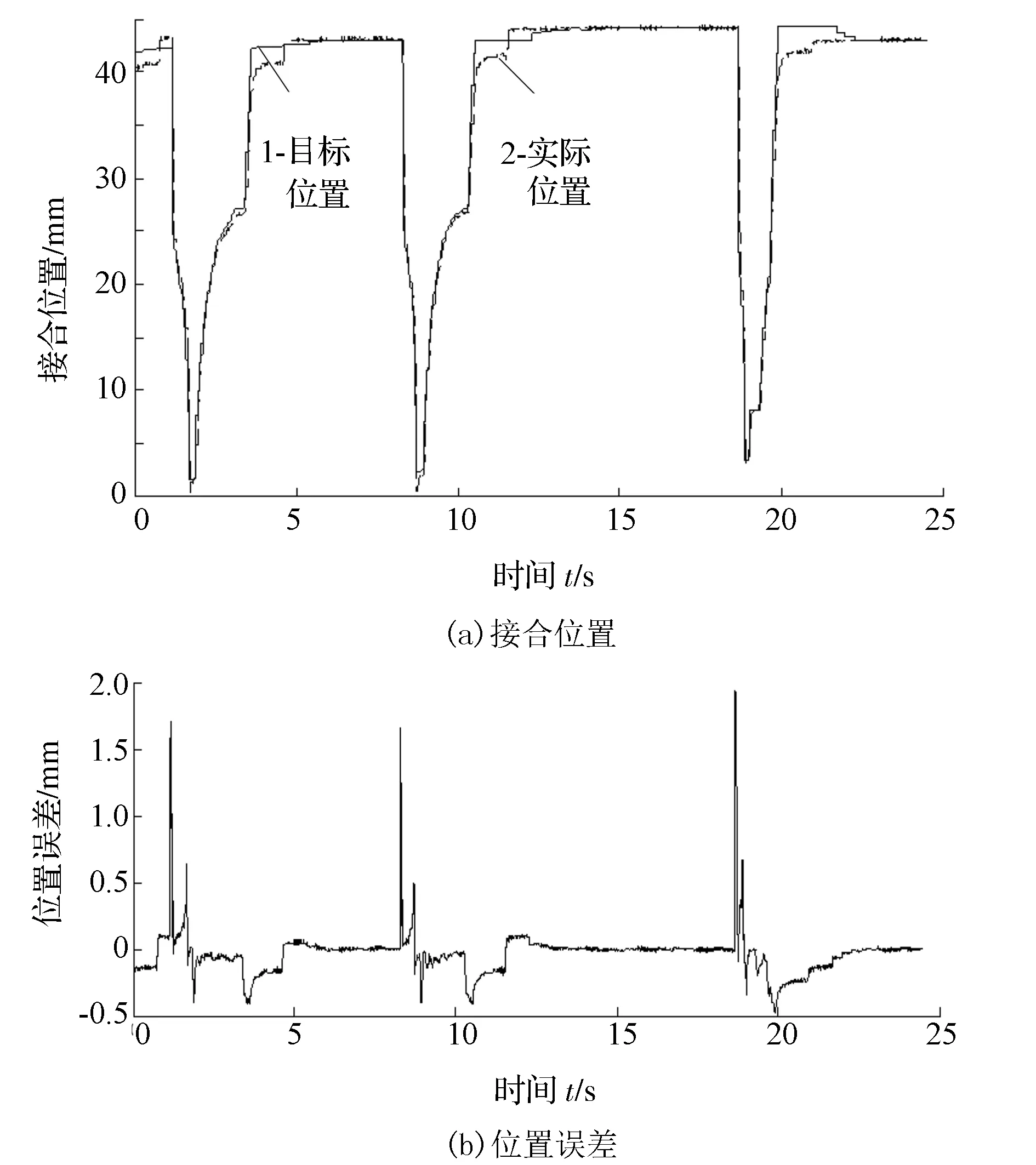
图11 升挡位置跟踪和跟踪误差曲线

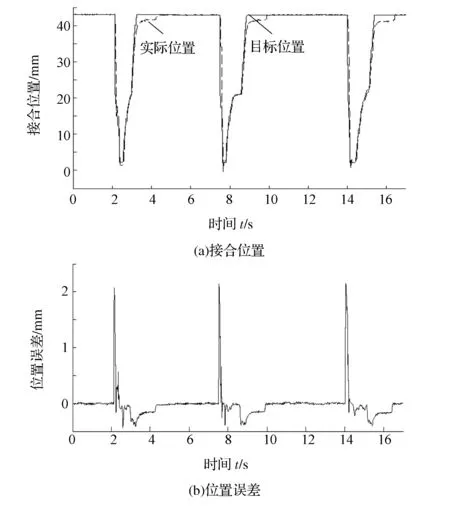
图12 降挡位置跟踪和跟踪误差曲线

4 结论

AMT自动离合器位置控制是一个模型较为复杂的非线性系统，本文中运用目前较为前沿的基于Udwadia-Kalaba方程的伺服约束控制对离合器位置跟踪进行控制。设计电流-位置双闭环控制系统将离合器接合规律视为一种约束，为满足该约束要求给系统施加一定的伺服约束力，利用Udwadia-Kalaba方程对伺服约束力进行求解。分别进行了台架和实车试验，结果表明，此控制器具有较好的鲁棒性和动态控制性能，基于Udwadia-Kalaba理论的离合器位置跟踪控制能较好地实现离合器位置的准确跟踪。

参考文献

[1]UDWADIA F E，KALABA R E.A new perspective on constrained motion[J].Proceedings of the Royal Society A， 1992， 439(1906)：407-410.

[2]UDWADIA F E，KALABA R E.On motion[J].Journal of the Franklin Institute， 1993， 330(3)： 571-577.

[3]UDWADIA F E，KALABA R E.Nonideal constraints and lagrangian dynamics[J].Journal of Aerospace Engineering， 2000， 13(1)：17-22.

[4]UDWADIA F E，KALABA R E.On the foundations of analytical dynamics[J].International Journal of Non-Linear Mechanics，2002，37(6)：1079-1090.

[5]UDWADIA F E.A new perspective on the tracking control of nonlinear structural and mechanical systems[J].Proceedings of the Royal Society A Mathematical Physical＆ Engineering Sciences，2003，459(459)：1783-1800.

[6]CHEN Y H.Second-order constraints for equations of motion of constrained systems[J].IEEE/ASME Transactions on Mechatronics， 1998， 3(3)： 240-248.

[7]CHEN Y H.Equations of motion of constrained mechanical systems： given force depends on constraint force[J].Mechatronics，1999，9(4)：411-428.

[8]CHEN Y H.Mechanical systems under servo constraints：the Lagrange’s approach[J].Mechatronics， 2005， 15(3)： 317-337.

[9]CHEN Y H.Equations of motion of mechanical systems under servo constraints： The maggi approach[J].Mechatronics， 2008， 18(4)：208-217.

[10]CHEN Y H.Constraint-following servo control design for mechanical systems[J].Journal of Vibration ＆ Control， 2009， 15(3)：369-389.

[11]CHEN Y H，ZHANG X.Adaptive robust approximate constraintfollowing control for mechanical systems[J].Journal of the Franklin Institute， 2010， 347(1)： 69-86.

[12]CHEN Y H，CHEN Y H.Approximate constraint-following of mechanical systems under uncertainty[J].Nonlinear Dynamics＆Systems Theory， 2008， 8(4)： 329-337.

[13]BAJODAH A H，HODGESD H，CHEN Y H.Inverse dynamics of servo-constraints based on the generalized inverse[J].Nonlinear Dynamics， 2005， 39(1)： 179-196.

[14]SCHUTTE A D.Permissible control of general constrained mechanical systems[J].Journal of the Franklin Institute， 2010， 347(1)：208-227.

[15]孙承顺，张建武，程东升.反馈线性化与滑模控制方法在汽车AMT中的应用[J].系统仿真学报，2004，16(4)：630-633.

[16]陈俐，张建武.汽车电控离合器的反馈线性控制[J].上海交通大学学报，2000，34(3)：384-388.

[17]程东升，张建武，孙承顺.车辆AMT离合器离散变结构控制[J].农业机械学报，2003，34(1)：31-34.

[18]赵和平，刘奋，张建武.自动离合器的变结构控制方法研究[J].农业机械学报，2002，33(2)：24-27.

[19]OZGUNER U， HONG S， PAN Y.Discrete-time sliding mode control of electronic throttle valve[C].IEEE Conference on Decision ＆ Control， 2001， 2：1819-1824.

[20]RIGATOSG G，TZAFESTASCS，TZAFESTASSG.Mobile robot motion control in partially unknown environments using a sliding-mode fuzzy-logic controller[J].Robotics＆Autonomous Systems， 2000， 33(1)： 1-11.

[21]UDWADIA F E， KALABA R E.Analytical dynamics：A new approach[M].Cambridge：Cambridge University Press，1996：58-66.

[22]姜建满，赵韩，赵晓敏.AMT自动离合器的变论域模糊控制[J].汽车工程，2016，38(9)：1080-1085.