激波管聚酯膜片变形过程分析*
2019-03-28何起光陈小伟徐剑鹏
何起光,张 伟,陈小伟,徐剑鹏
(1. 哈尔滨工业大学航天学院高速撞击动力学实验室,黑龙江 哈尔滨 150001;2. 北京理工大学前沿交叉科学研究院,北京 100081)
激波管已广泛用于航空、化学动力学、等离子体物理等领域。近年开始使用聚酯薄膜作为激波管的膜片以替代原来的金属膜片,并出现了多种破膜方法[1-2]。聚酯薄膜作为膜片具有价格低廉、便于安装、易于控制破膜压力等优点。膜片安装在激波管的高压段与低压段之间,当高压段内气体压力超过膜片承载时,膜片将破裂。高压气体向低压段方向传播并产生激波。激波的强度、速度和激波位置与高压段内压力有关,同时与膜片破坏形状和破坏形式有关。所以,获得膜片在高压段内充压过程中的变形规律对激波管激波分析是有意义的。
Nguyen等[3]研究了膜片承载与膜片厚度的关系。Gharababaei等[4]给出了金属薄板在静态压力下变形的数学规律。Bradley等[5]使用理想的变形模型对激波管中的膜片变形进行过分析。Barsoum等[6]、Rothkopf等[7]和Campbell等[8]研究了膜片破坏时的速度与形状对激波的影响。佟富强等[9]和黄官强等[10]对聚酯薄膜的一维应力应变关系进行过深入研究,得到了单向拉伸的应力应变关系。以上研究都局限在弹性变形范围,假设薄膜为圆弧状变形,而对后续更严重变形没有涉及。
本文中主要研究不同厚度的聚酯薄膜在不同压力下的变形全过程。发现接近破坏时,膜片会出现圆弧反翘的现象。以此为依据,将全过程分为2个阶段,给出膜片变形过程的数学规律。
1 实验装置
如图1所示,实验装置由高压段、靶舱和高速摄像机组成。其中,高压段长128 mm,直径为66 mm,最大承受压力为20 MPa。通过压力传感器测量高压段的压力。在高压段的管口,使用夹具装有不同厚度的聚酯薄膜膜片。本实验采用常州新遥光绝缘材料有限公司生产的BE12型号的PET聚酯薄膜作为膜片。如图2所示,采用GB/T1040标准对聚酯薄膜进行常温下准静态拉伸,获得膜片纵向及横向的应力应变曲线。可以看出,薄膜两个方向的弹性模量近似相等,但在塑性阶段,受制作工艺影响,其拉伸强度和硬化模量存在较大差异。

图1 实验装置示意图及照片Fig. 1 Schematic diagram and photo of experimental equipment
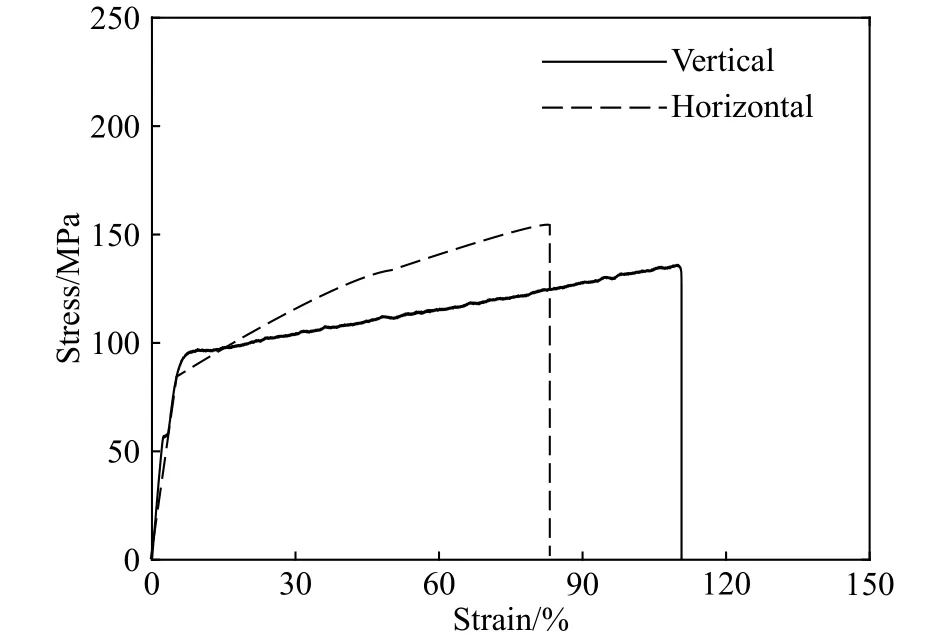
图2 膜片的应力应变曲线Fig. 2 Stress-strain curves of the diaphragm
三维DIC技术全称数字图像相关技术,使用两台摄像机对已有散斑的试件进行拍摄后,运用光学原理对某一时刻两个视角的照片进行处理后,可获得试件上各点当前时刻在空间中的坐标。本实验中,使用两台高速摄像机同步记录膜片的破坏过程后,用DIC分析软件ARAMIS对所获得的照片进行计算,获得膜片从充气到破坏的变形历程。在本实验中,压力增速约为12 kPa/s。
2 膜片破坏压力与其厚度的关系
在激波管实验中,可采用单膜或多膜结构的聚酯薄膜膜片。膜片的最大承载直接决定激波管高压段内压力大小,而这与聚酯薄膜膜片的厚度有直接关系。本文考虑0.05、0.1和0.2 mm三种不同厚度聚酯薄膜组合,以此获得不同厚度或同厚度下不同组合的薄膜承载能力。
在上述实验装置中安装不同厚度与不同组合方式的膜片。在高压段中逐渐增加气体压力,由压力传感器得到高压段内的压力。表1给出膜片破坏压力,共有8种不同厚度的不同组合方式。由表1可知,在相同厚度的条件下,不同的膜片组合对膜片最大破坏压力影响甚小。可认为:同种材质、同种实验环境下的聚酯薄膜膜片的最大破坏压力仅与其厚度有关,与组合方式无关。

表1 不同膜片组合及厚度的最大破坏压力Table 1 The maximum bearing pressure of different diaphragms thickness and combinations
用最小二乘法拟合表1的数据,获得最大破坏压力pmax与膜片厚度δ的关系见图3,图中直线方程为:

式中:斜率k受材料及制作工艺的影响,本实验中k=5.56 GPa/m。各条件下的k可由同样方法得到。
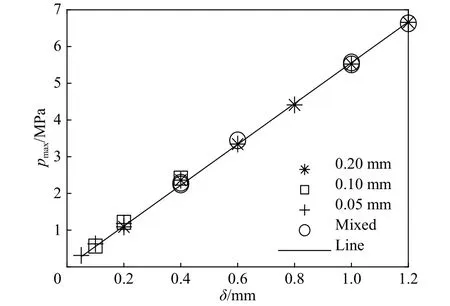
图3 不同厚度及组合方式的膜片的破坏压力Fig. 3 Maximum bearing pressure of diaphragm with different thickness and combination
3 膜片变形规律
为研究聚酯薄膜膜片的破坏过程,需获得膜片在不同压力下对应的变形。在不同厚度的膜片表面绘制5 mm×5 mm的网格,使用高速相机记录膜片的变形过程。图4 给出了三种厚度膜片在不同压力下的变形过程,可以看出,膜片中心的网格变形最大,四周较小,网格变形基本呈轴对称分布。
使用三维DIC技术进一步观察膜片的变形,将两台相机同步记录的图片导入ARAMIS软件进行计算后可得膜片的位移场。图5为0.2 mm厚的膜片在不同压力条件下的变形图。与图4相同,膜片位移场呈轴对称变化,中心处位移最大,因此可由轮廓曲线描述膜片完整形状。

图4 三种厚度的膜片在不同压力条件下的变形Fig. 4 Deformation of diaphragms with three different thicknesses under different pressures

图5 DIC处理后所得不同压力条件下0.2 mm厚膜片变形的典型结果Fig. 5 Deformation of diaphragm with 0.2 mm in thickness by 3D-DIC analysis
图6给出了三种厚度的膜片在不同压力下的轮廓曲线。可以看出:随着压力增加,膜片轮廓曲线由圆弧形状逐渐变化为仅头顶部呈圆弧的锥形,最后锥形两侧的直线发生内凹现象,出现圆弧反翘。当轮廓曲线刚出现内凹时,以该锥形作为其极限轮廓,用两条虚线表示,可将变形过程分为2个阶段:第1阶段为前7条曲线,即轮廓曲线在极限轮廓内变化,其中前3条曲线呈圆弧状,各点曲率大致相等且逐渐增大,第4至第7条曲线达到极限轮廓的部分挠度近乎不变,基本呈现直线,而圆弧部分各点曲率仍大致相等且继续增大;第2阶段为后2条曲线,轮廓曲线开始超过极限轮廓,轮廓曲线中央部分出现反翘现象,曲线中点的挠度、曲率迅速增大直至膜片破坏。
对于不同厚度的膜片,图6中虚线的斜率基本相等,平均值为0.73。令轮廓曲线即将超过极限轮廓时对应压力临界点为Qi,膜片破坏时对应压力临界点为,其中i=1,2,3,分别代表厚度为0.05、0.1和0.2 mm三种膜片,如图7所示。表2给出了这6个点的压力及挠度参数,其中:k′为各点压力与厚度之比,为不同厚度k′的平均值。在Qi*处,即有k′=k;根据表 2,在 Qi处,k′=0.974k,此时:
式中:p为压力;Zmax为膜片中心挠度,即最大挠度;a≈4.100×10-12m2/Pa。
膜片的应变场可由位移场计算得到。显然,膜片的应变分布也是轴对称的,只需考虑轮廓曲线上的应变分布。由于Gharababaei等[4]对鼓包后金属薄板的应变计算方法是连续的,但DIC获得的数据是离散点的位移信息,所以对其离散化后得到:
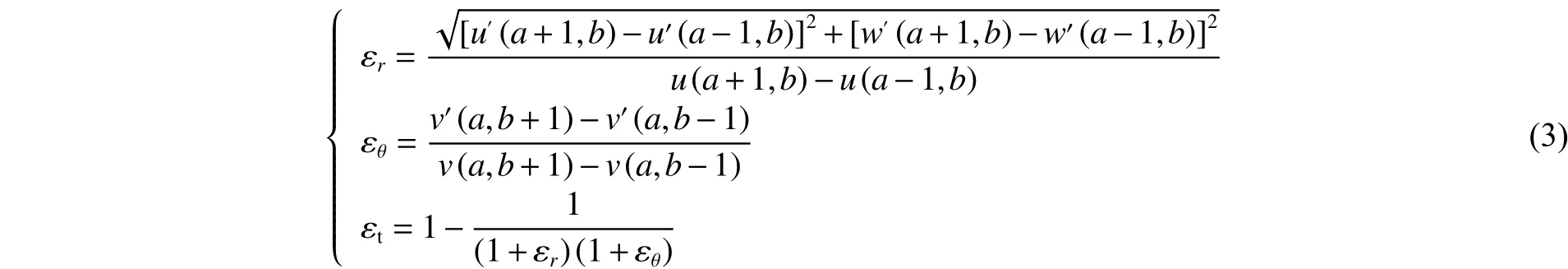
式中:a和b分别表示网格节点在x和y方向的编号;u和v分别表示节点在x和y方向的初始坐标;u′、v′和w′分别表示在x、y和z方向变形后的坐标;εr,εθ分别为径向应变和环向应变;εt为厚度减少的百分比。
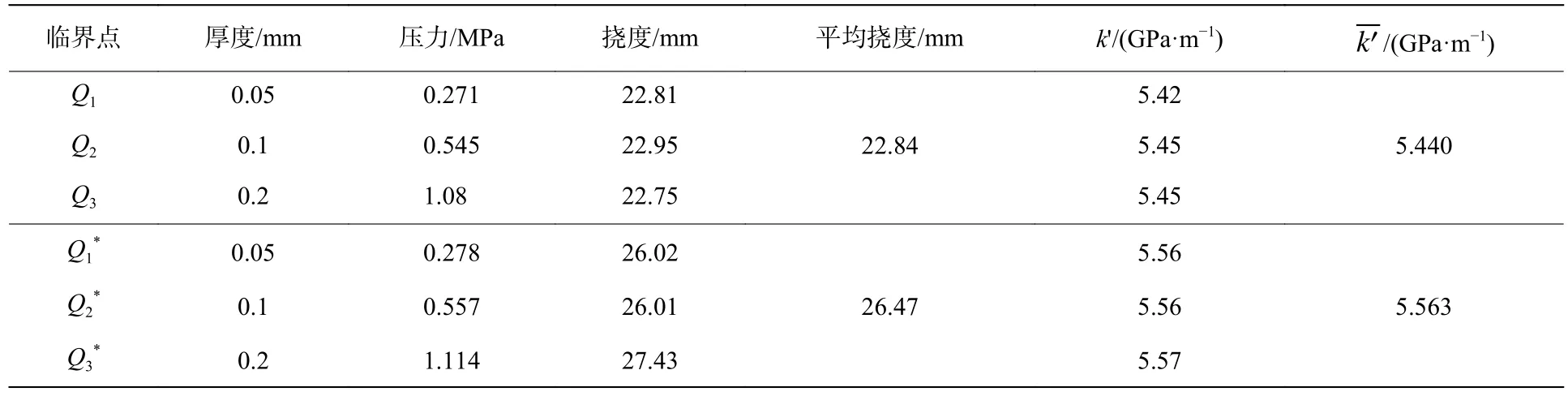
表2 三种不同厚度膜片临界点的数据Table 2 Data of critical point in diaphragm with three different thickness
由式(3) 计算所得膜片厚度变化情况如图8所示,图中曲线与图6中曲线分别对应。膜片大变形时,边缘处与相机的夹角很小,会造成较大的计算误差,所以仅给出膜片中间部分的厚度变化分布。可以看出:处于第1阶段的膜片厚度变化较为均衡,中间处的厚度较边缘减少量略多,厚度略小,分布的形状近似于一段圆弧。随着压力的增加,膜片厚度的变化逐渐加快。在第2阶段中,分布呈锥形,中心处膜片的厚度最小且远小于膜片边缘的。膜片中心处厚度随着压力的增加快速减小,距离中心点越远,厚度的变化速度越慢。中心处也是膜片破裂位置。
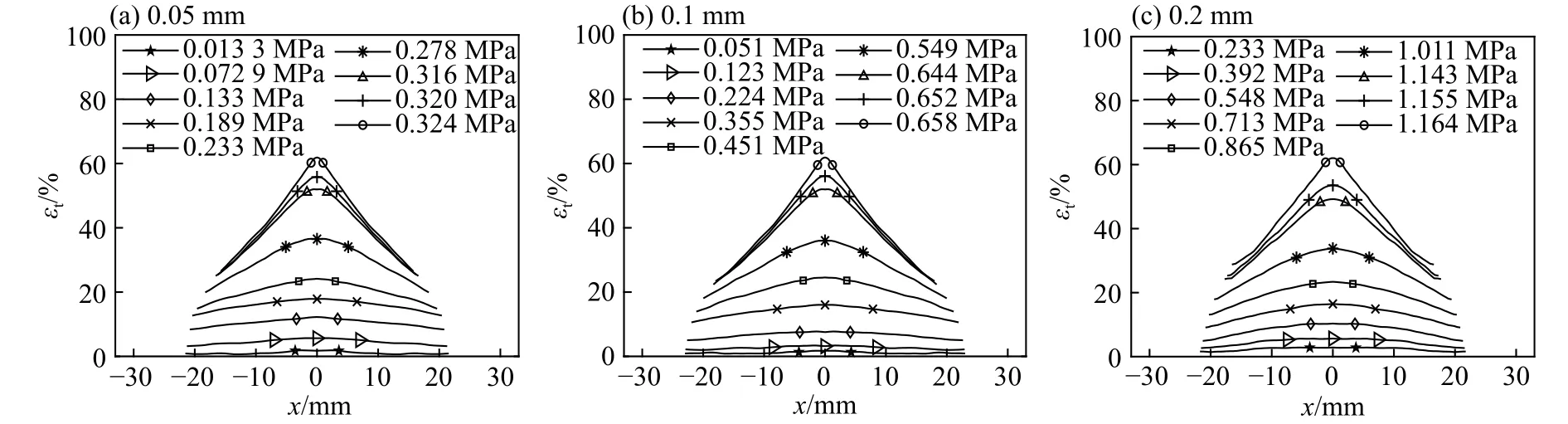
图8 膜片厚度减小量的分布曲线Fig. 8 Distribution curves of thickness reduction
图9给出三种初始厚度膜片的中心处厚度变化与压力的关系。与中心处挠度与压力的关系类似,三条曲线的趋势是相似的,仅斜率不同。受膜片初始厚度的影响,三条曲线的斜率与膜片的初始厚度也呈反比关系。
4 膜片变形规律的数学模型
根据表2中Qi点的压力数据可知,对于厚度为δ的膜片,p0.974kδ为第1阶段,p0.974kδ为第2阶段,p=0.974kδ为膜片即将出现反翘现象的压力。
对于第1阶段,使用最小二乘法对图7进行拟合,并代入激波管内径与膜片初始厚度的参数,在数学上使用两段线拟合第1阶段曲线,可以得到经验公式:

式中:R为激波管半径。
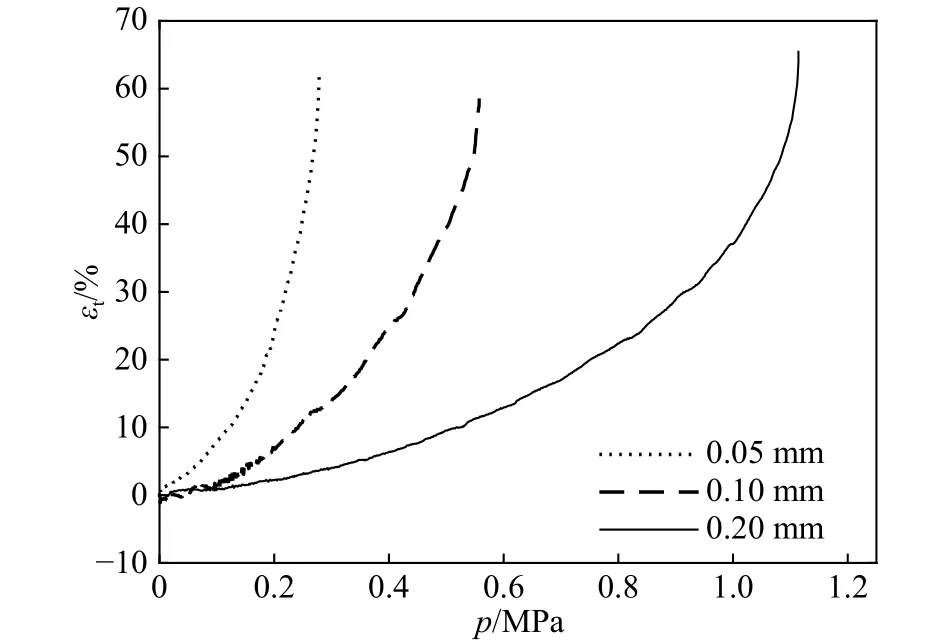
图9 膜片中心的厚度减小量与压力曲线Fig. 9 Relation between maximum thickness reduction of diaphragm and pressure

将式(4)~(6)的计算结果与实验结果对比,如图10所示。可以看出:由式(4)计算所得三种厚度膜片的最大挠度与压力的关系曲线与实验结果对比吻合较好(图10(a));对于圆弧半径(图10(b)),由于式(5)和(6)中使用了式(4)的计算结果,误差累计导致0.2 mm厚度的曲线左端误差较大,但总体而言,计算结果与实验结果吻合较好。由于圆弧的半径和最大挠度决定直线部分长度,后者误差取决于前两者误差,所以直线部分长度误差同样较小。
膜片厚度的变化直接取决于膜片的变形状态,而图9中曲线与图7类似,可将膜片中心处最大挠度与厚度变化相联系。利用式(4)结果,得到膜片中心处厚度变化与挠度之间的关系:

将式(4)代入式(7),可计算膜片中心厚度减少量,如图11所示。

图10 模型计算所得曲线与实验结果的对比Fig. 10 Contrast of deflection and radius between experiment and calculation

图11 模型计算所得膜片厚度变化与实验结果的对比Fig. 11 Contrast of thickness between experiment and calculation
5 结 论
本文对激波管聚酯膜片的最大承载进行试验,得到膜片的最大承载与其组合方式无关,仅与其厚度相关且呈线性关系。使用DIC技术对膜片破坏全过程进行观察分析,获得膜片从静止到破坏全过程的变化规律,观察到膜片在破坏前出现圆弧反翘的特别现象。以出现反翘为判据,将整个过程分为2阶段,给出了任意厚度膜片在第一阶段圆弧变形过程中最大挠度与压力及膜片形状的关系,以及膜片在第二阶段圆弧反翘的变形特征。对数据进一步处理获得了膜片在变化过程中的厚度变化,及其与膜片最大挠度的关系。
