计入曲轴油道机油流动的轴承弹流润滑分析∗

潘俊杰，杨 靖，刘伟强，刘凯敏，冯仁华

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.湖南大学，湖南省绿色汽车2011协同创新中心，长沙 410082；3.重庆理工大学，汽车零部件先进制造技术教育部重点实验室，重庆 400054)

前言

曲轴轴承作为发动机的主要承载零件之一，其润滑情况直接影响发动机的工作状态、可靠性和寿命。由于发动机一直朝着高速和大功率的方向强化，曲轴轴承的工作环境越来越恶劣，完善曲轴轴承润滑理论、精确轴承润滑状态和性能预测变得越来越重要。

发动机轴承润滑分析现已日趋完善，基于弹流润滑(elasto-hydrodynamic)、热流润滑[1](thermo-hydrodynamic)和热弹流润滑[2](thermo-elasto-hydrodynamic)等研究基础，考虑了曲轴和缸体受载变形[3]、粗糙表面摩擦[4]和热变形[5]等因素的影响。但这些研究多未涉及曲轴油道内的流动分析，主轴承和连杆轴承的供油压力、温度等边界条件往往直接给定[6]，对二者润滑状态之间的联系研究较少。事实上，曲轴高速转动或加速时，曲轴油道内的润滑油油压在离心力和科氏力的作用下易急剧下降至饱和压力以下，在油道内形成空穴、机油呈不连续现象，加速轴承穴蚀现象的发生，破坏轴瓦、影响发动机的正常工作。而且，连杆轴承的机油由主轴承提供，其供油压力、机油温度与主轴承密切相关，通过油道流动分析来给定连杆轴承的边界条件对准确研究连杆轴承润滑有重要意义。

本文中引入Bernounlli流动方程分析油道内机油的流动情况，并搭建空穴模型模拟油道内的空穴现象，对一四冲程汽油机的某连杆轴承及其相应主轴承进行弹性流体动力润滑分析，通过与不计油道内流动的情况比较分析，探讨曲轴油道内的机油流动情况及其对主轴承和连杆轴承的润滑分析的影响。

1 基本理论、方程与模型

1.1 油道内流动Bernoulli方程

搭建油道内润滑油流动的数学模型时，须在准稳态不可压流体简化模型的基础上假设油道为圆柱面，对油道采取等温边界条件并假设机油在油压低至空穴压力以下时立即蒸发。假设连续截面油道两端点坐标为χ1和χ2，对油道列出Bernoulli方程：

式中：ρ为机油密度；W为机油轴向流速；p为机油压力；Y1，2为油道端点1到2的总能量损失，包括油道壁面摩擦损失和出入口流动损失；ζ为端点处的能量损失系数；Dp为油柱边界力密度，包含约束力项角加速度项和离心力项；ε为参考坐标系下平移运动矢量；Ω为角速度矢量。

流经油孔处的机油包括流入轴径油膜、流入轴瓦油槽和流入油道3部分，对油孔采用Kirchoff准则建立连续性边界条件。

(1)流量边界条件

式中：q1，q2和q3分别为流入轴颈油膜表面、流入供油油槽和流入油道内的机油流量。

(2)压力边界条件

式中：p1，p2和p3分别为轴径油膜表面、轴瓦油槽和油道在油孔处的机油压力。

1.2 油道空穴模型

引入空穴模型模拟油道内油压低于润滑油饱和压力pvap时发生的空穴现象，同时考虑油道内可能发生的枯涸和回流情况。在油道油压降至pvap处，油柱断裂为两段并用Bernoulli方程分别对其模拟，机油压力p与油道距离坐标l关系如图1所示，油道边界条件如下。

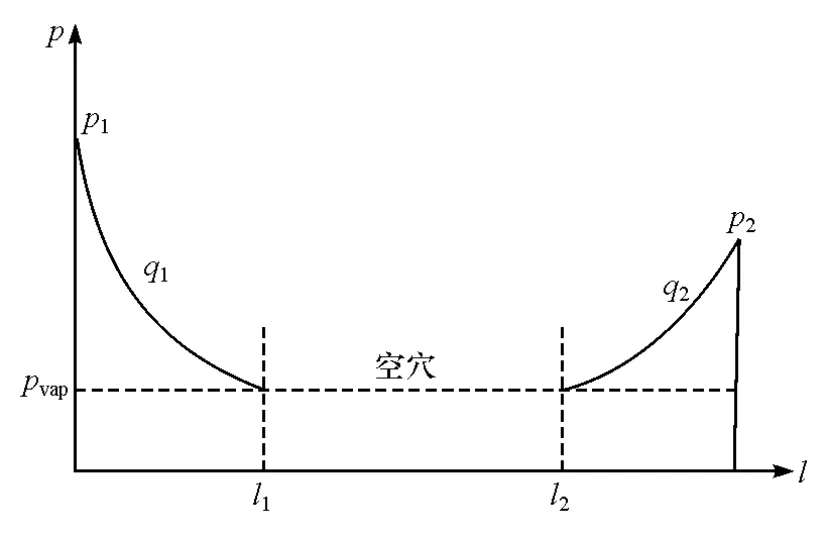
图1 油道空穴模型原理示意

(1)实际油柱长度变化率

式中：l为油柱从断裂处到该段油道端点的实际距离；t为时间坐标；q为机油流量；A为油道截面积。

(2)油柱端点压力

原端点处，p＝pi

油柱断裂处，p＝pvap

式中pi为端点i即1或2处的机油压力。

1.3 主轴承和连杆轴承弹流润滑的Reynolds方程

针对主轴承和连杆轴承的润滑引入扩展Reynolds方程进行模拟，方程由Navier Stokes方程和连续性方程扩展得到[7]，并考虑表面粗糙度、机油填充率和轴瓦变形等的影响。

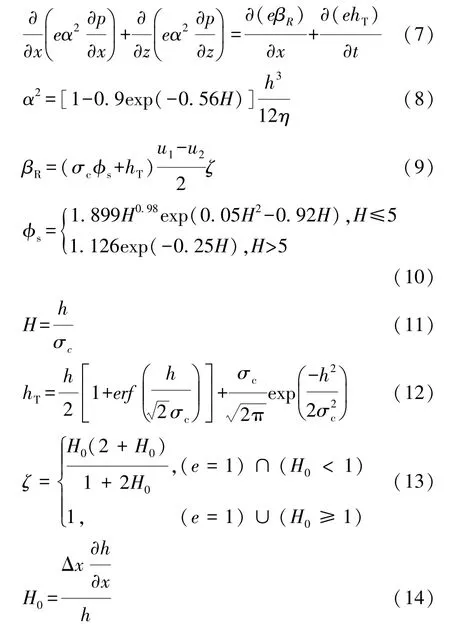
式中：x和z为轴承周向和轴向坐标；e为机油填充率；p为油膜压力；φs为剪切流量因子[8]；h为间隙厚度；η为机油动力黏度；hT为考虑粗糙表面的轴瓦与轴颈间隙，erf(·)为误差函数；σc为综合粗糙度；u1和u2分别为轴颈和轴瓦的周向速度。

1.4 粗糙接触压力模型

主轴承和连杆轴承轴颈与其轴瓦间的粗糙接触压力pa采用Greenwood/Tripp模型[9]进行计算，假设所有表面粗糙峰值服从正态分布或高斯分布，平均接触压力pa近似存在如下的指数关系[10]：

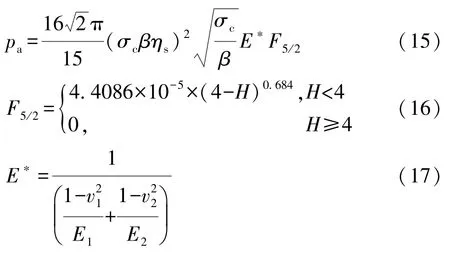
式中：β为微凸峰值曲率半径；ηs为单位面积内的微凸峰数量；E1，E2和v1，v2分别为轴颈和轴瓦材料的弹性模量和泊松比。

1.5 主轴承和连杆轴承载荷

主轴承和连杆轴承载荷在x轴和z轴的分力[11]分别为

而其合力则为

式中Rj为轴颈半径。

1.6 主轴承和连杆轴承的摩擦力和端泄油量

主轴承和连杆轴承切向应力与压力相同，包括流体切应力τ和摩擦接触切应力τa，则摩擦力Ff和摩擦损耗功率为

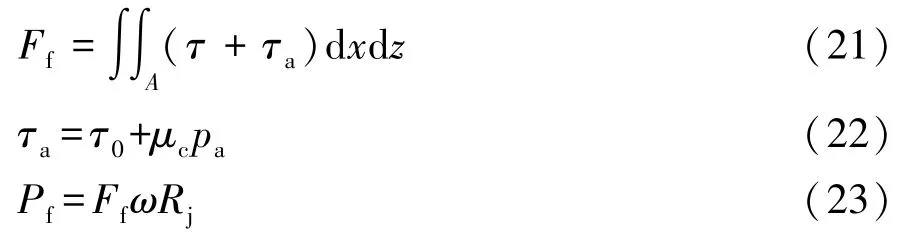
式中：τ0为边界剪切强度；μc为边界润滑的摩擦因数。

由轴承前端面和后端面流出的机油流量[13]为

即轴承端泄油量为

2 润滑特性仿真结果与分析

本文中对某汽油机曲轴的润滑特性进行数值分析，主要研究连杆轴承和对其供油的主轴承的润滑情况，故仅取某一连杆轴承及其相应主轴承模型进行数值分析以减少计算量。图2为发动机部分机体和连杆有限元模型，缸体模型将部分缸体、主轴承盖和轴瓦等零件统一划分为四面体单元网格，共74 885个网格、128 529个节点，连杆模型将轴瓦、连杆盖和连杆螺栓处理为一整体，划分为四面体网格单元，共44 797个网格、80 601个节点。

图2 部分机体与连杆有限元模型

为方便进行润滑计算时有限元节点位移与雷诺差分节点边界条件的相互迭代，划分网格时保证轴瓦内表面网格数目与雷诺差分网格数目相互对应。缩减时缸体仅保留轴承表面节点的主自由度，连杆保留连杆大、小头表面节点和耦合质心点的主自由度，轴颈保留轴心上节点的主自由度。连杆轴颈油道交汇于主轴颈油道靠近一端油孔处，图3为油孔与油道示意图，在0°CA(压缩上止点)位置，油孔1和油孔2在主轴颈周向方向上的角度分别为60°和220°，油孔3在连杆轴颈的周向方向角度为38°。

图3 曲轴油道及油孔示意图

曲轴主轴承和连杆轴承的详细参数如表1所示。

表1 主轴承与连杆轴承详细参数

2.1 油道内流动情况分析

对曲轴油道内的机油流动情况和各位置机油压力分布进行模拟计算，主轴承和连杆轴承的油孔压力由油道内流动分析决定，油孔内壁粗糙度为3.2μm，油孔流入和流出阻力系数分别为0.8和1，主轴瓦油槽的供油压力为0.5MPa，上、下轴瓦分界处压力为环境压力0.1MPa，分析结果针对第2工作循环(720°～1 440°CA)给出。 图 4给出了 765°和1 090°CA(压缩上止点为720°CA)下油道内的液动压力分布情况，这两个曲轴转角下油道内压力分别分布在0.05～0.24MPa和0.42～0.66MPa之间，均大于润滑油饱和压力0.01MPa。

图5示出各油孔处的液动压力在一个工作循环中的变化情况，油孔处压力由大到小顺序依次为1，4，2和3，与图4结果吻合。随着曲轴的转动，各油孔的油压变化趋势一致，在760°和1 120°CA下油压剧烈下降至约0.44MPa，原因是油孔1和油孔2随主轴颈转至上下轴瓦分界线处，此处环境压力仅有0.1MPa；在930°～960°CA 和1 290°～1 320°CA 内出现油压波动，是由油孔1和油孔2随主轴颈转动转至油槽以外所致。

图4 不同曲轴转角下的油道内油压分布

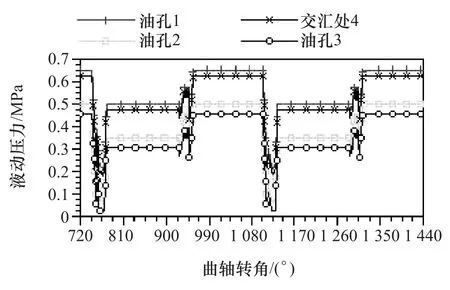
图5 各油孔处的液动压力

图6为不同油孔流至油道交汇点4处的机油流量。由图可见：来自主轴颈油孔的机油流量较大，这是由于多数曲轴转角下主轴承两油孔处油压力差别较大；流向连杆轴颈油孔的流量仅在主轴颈油孔转至轴瓦分界处时出现过波动，油孔1和油孔2随主轴颈转至油槽以外时，出现从油孔1到油孔2的较大流量，随后出现流量较大的反向机油流动。图7分别示出由油孔3和交汇点4起的油道3内油柱长度图。由图可见，在760°和1 120°CA下出现交汇点4至油孔3的机油流动并随后回流，未出现油道内空穴现象。

图6 各油道经过交汇点4处的流量

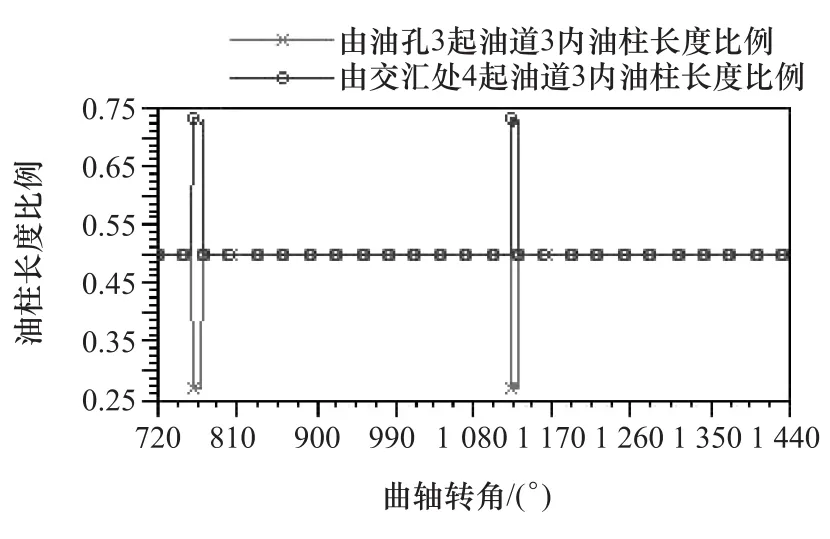
图7 由各油孔起的油道3内油柱长度

2.2 计入与不计油道流动的曲轴轴承润滑分析对比

常规曲轴轴承润滑分析并不考虑油道的流动，而是分别给出主轴承和连杆轴承各自的边界条件并进行相对独立的润滑分析。计入油道内流动的分析能将主轴颈与连杆轴颈油孔处的动态油压关联起来，并计入二者之间的相互影响，从而得到更加精确的曲轴轴承润滑分析结果。

在相同工况下分析考虑与不考虑油道内流动时曲轴的流动润滑特性并进行对比，不考虑油道流动时主轴颈和连杆轴颈的油孔供油压力分别设为0.5和0.65MPa，计入油道内流动分析时二者由机油油道内流动计算结果给定。图8分别示出计入与不计油道内流动时主轴承和连杆轴承最大油膜压力在一个工作循环中的变化情况。由图可见：不计油道内机油流动时，主轴承最大油膜压力在730°CA时出现极值98MPa，计入油道分析后，极值为103MPa，计入油道流动分析对主轴承的最大油膜压力极值和变化趋势影响较小；计入油道流动分析对连杆轴承的最大油膜压力变化历程有较大影响，与直接设定连杆轴颈油孔压力相比，连杆轴承最大油膜压力几乎在整个工作循环内都有升高，最大油膜压力极值由153变化到了196MPa。计入油道流动分析主要影响连杆轴承的最大油膜压力，这是由于连杆轴承的润滑油是主轴承经油道供给的，其供油压力受曲轴油道内的流动情况影响较大。

图8 主轴承与连杆轴承最大油膜压力

图9分别示出计入与不计入油道流动时主轴承和连杆轴承最小油膜厚度在一个工作循环中的变化图。由图可见：计入油道流动在工作循环的大部分时间内对主轴承最小油膜厚度影响不大，但在1 080°～1 100°CA 和1 130°～1 220°CA下有一定影响，这主要是由于油孔处压力波动引起的；计入油道流动后，连杆轴承的最小油膜厚度在整个工作循环中降低了约0.3μm，降幅比较明显。其原因是计入油道流动后，连杆轴承的供油压力和供油量变小。

计入与不计油道流动时主轴承与连杆轴承的端泄油量如图10所示。由图可见：计入油道流动后的主轴承端泄油量与不计油道流动的变化趋势一致，仅在个别曲轴转角范围内有小幅变化；计入油道流动后的连杆轴承端泄油量对比不计油道流动分析时在 720°～800°CA 和 1 130°～1 190°CA 范围内有明显减小，主要由于计入油道流动后连杆轴颈油孔处的油压在该曲轴转角下的剧烈变化引起的。

图9 主轴承与连杆轴承最小油膜厚度

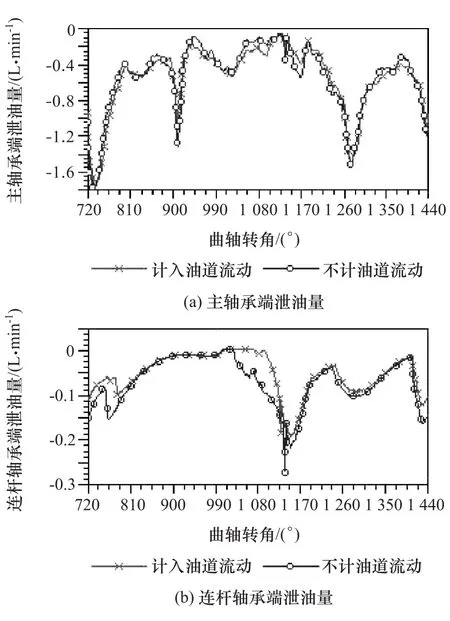
图10 主轴承与连杆轴承端泄油量

计入与不计油道流动时主轴承和连杆轴承在一个工作循环内的摩擦损失功率如图11所示。由图可见：计入油道流动后主轴承的摩擦损失功率整体趋势未发生变化，最大摩擦损失功率由0.58升高至0.66kW，升高幅度较小；计入油道流动后，连杆轴承的摩擦损失功率变化趋势也未发生变化，但最大摩擦损失功率升高了53%，由0.45升高到了0.69kW。计入油道内流动后连杆轴承的最大摩擦损失功率升高明显，主要由于连杆供油边界条件由分析计算给定，连杆轴承的最大油膜压力极值变大，平均最小油膜厚度减小，故摩擦损失功率增加。

图11 主轴承与连杆轴承摩擦损失功率

3 结论

(1)搭建主轴承与连杆轴承的弹性流体润滑模型，引入油道内流动Bernoulli方程来分析油道内机油流动情况并搭建油道空穴模型模拟穴蚀现象。计算出油道内的机油压力分布和通过各油孔的机油流量，油道流动分析与轴承润滑分析结果一致。

(2)油道内流动分析表明，主轴颈油孔压力高于连杆轴颈油孔压力，油道内机油压力在主轴颈油孔转过上下轴瓦分界线时急剧下降，降幅超过60%，主轴颈油孔转动至轴瓦油槽以外时，油道内压力出现波动情况，整个分析过程中油道内机油油柱保持连续、未出现穴蚀现象。

(3)计入油道流动对主轴承的润滑分析影响较小，最大油膜压力、最小油膜厚度和端泄油量等随曲轴转角的整体趋势未变化，只在个别曲轴转角范围内出现小幅变化。

(4)计入曲轴油道流动后，连杆轴承的最大油膜压力升高了28%，最小油膜厚度在整个工作循环内减小约0.3μm；在油道压力出现剧烈变化的曲轴范围内，连杆轴承的端泄油量出现显著降低；连杆轴承在压缩上止点附近的摩擦损失功率升高了53%，最大摩擦损失功率升高极为明显。因此，进行连杆轴承的润滑分析时，考虑曲轴内油道流动情况能给出更精确的连杆轴承边界条件，对连杆轴承润滑分析、连杆强度和疲劳分析等具有重要意义。

参考文献

[1]SHARMA SC，KUMAR V，et al.Study of hole-entry journal bearings system considering combined influence of thermal and elastic effects[J].Tribology International，2003，36(12)：903-920.

[2]OKAMOTO Y.Numerical analysis of lubrication in a journal bearing by a thermoelastohydrodynamic lubrication(TEHL)model[J].Tribology International，2003，36：903-920.

[3]PIFFETEAU S，SOUCHET D，BONNEAU D.Influence of thermal and elastic deformations on connecting-rod big end bearing lubrication under dynamic loading[J].ASME Journal of Tribology，2000，122(1)：181-191.

[4]邓枚，孙军，符永红，等.计及曲轴受载变形的粗糙表面轴承热弹性流体动力润滑分析[J].机械工程学报，2010，46(15)：95-101.

[5]童宝宏，桂长林，孙军，等.计入热变形影响的内燃机主轴承热流体动力润滑分析[J].机械工程学报，2007，43(6)：180-185.

[6]KIM Byung-jik，KIM Kyung-woong.Thermo-elastohydrodynamic analysis of connecting rod bearing in internal combustion engine[J].ASME Jourinal of Tribology，2001，123(3)：444-454.

[7]GARNIER T.Three-dimensional EHD behavior of the engine block/crankshaft assembly for a four cylinder inline auto-motive engine[J].ASME Journal of Tribology Transaction，1999，121(4)：721-730.

[8]PADIR N.Application of average flow model to lubrication between rough sliding surfaces[J].Transactions of the ASME，1979，101：220-230.

[9]GREENWOOD J A，TRIPP J H.The contact of nominally flat rough surface[J].Proc Inst Mech Engr，1970，185(46)：625-633.

[10]魏立队，魏海军，段树林，等.基于机体与曲轴耦合下的船舶柴油机主轴承热弹性流体动力混合润滑特性[J].机械工程学报，2014，50(13)：97-105.

[11]ZHANG C，et al.Fast analysis of crankshaft bearings with a database including shear thinning and viscoelastic effects[J].Tribology Transactions，1998，42(4)：922-928.

[12]温诗铸.摩擦学原理[M].北京：清华大学出版社，1991.

[13]孙军，王震华，桂长林.计入曲轴受载变形的粗糙表面曲轴轴承弹性流体动力润滑分析[J].机械工程学报，2009，45(1)：135-140.