三角形内角和的发现与证明

◇王丽娟

纵观几何发展史，三角形是人类认识较早的图形，不管是欧几里得的《几何原本》，还是中国的《九章算术》，都记载了许多关于三角形的定理，“三角形内角和等于180°” 就是其中一个重要的定理。

一发现

公元前6 世纪，古希腊哲学家泰勒斯（Thales，约公元前624—前547 或546年）很可能已经知道了三角形的内角和定理。毕达哥拉斯学派提出，只有三种正多边形（正三角形、正方形和正六边形）能密铺整个平面，据此推测，他们的前辈泰勒斯已经利用正三角形拼图进行数学探究。泰勒斯知道等腰三角形底角相等，等边三角形三个内角相等。他先把六个同样的等边三角形的顶点置于同一点，结果恰好填满该点周围区域，所以六个内角之和等于四个直角，那么三个内角之和就等于两个直角（如图1）。接着，将六个同样的等腰三角形的不同顶点置于同一点，其中每个顶点出现两次，结果也恰好填满该点周围区域，所以六个内角之和等于四个直角，三个内角之和等于两个直角（如图2）；最后用六个同样的不等边三角形来拼图，发现了同样的结果——三个内角之和等于两个直角，即180°（如图3）。

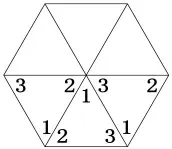
图1 等边三角形拼图

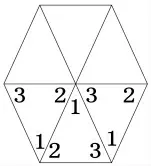
图2 等腰三角形拼图

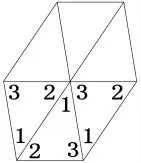
图3 不等边三角形拼图

关于三角形内角和定理的发现，还有一人不得不提，他就是法国著名科学家、数学家帕斯卡（Pascal，1623—1662年）。帕斯卡在12 岁的时候，没有任何书本的暗示，把一个三角形纸板经过折叠拼凑，发现了三角形三个内角的和等于平角这个结论，这也许是教科书中折叠拼凑实验的最初来源（如图4）。他发现当三角形三个内角折到一起时，可能三个顶点折到其内切圆的圆心上或者折到垂足处都是一个平角，由此得出三角形内角和等于180°。之前，为了避免体弱多病的帕斯卡用脑过度，父亲不让他接触数学，但当父亲发现了帕斯卡惊人的几何才能后，送给他一本欧几里得的《几何原本》，年幼的帕斯卡很快熟练掌握了它，以此为基础开启了他的数学研究之旅。

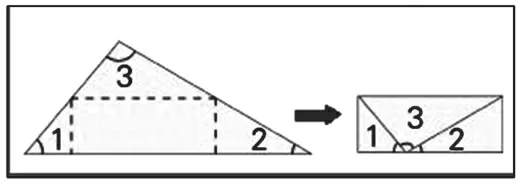
图4 折纸法

二西方数学家的证明

1.毕达哥拉斯与欧几里得的方法。

毕达哥拉斯学派在几何学上做出的具体成就很多，最著名的就是证明了毕达哥拉斯定理（即勾股定理）和三角形内角和定理。他们在泰勒斯的基础上，发现了更多的几何定理，其中“两直线平行，内错角相等”及其逆定理，使得毕达哥拉斯证明三角形内角和定理水到渠成。 如图5，过三角形ABC 的顶点A 作BC 的平行线DE，∠ABC=∠BAD, ∠ACB=∠CAE（两直线平行，内错角相等），因为∠BAC＋∠BAD＋∠CAE=180°（平角的意义），所以∠BAC＋∠ABC＋∠ACB=180°（等量代换），即三角形内角和等于180°。

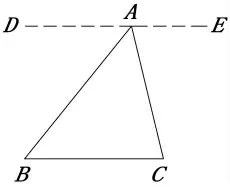
图5 毕达哥拉斯的证明

毕达哥拉斯通过两组内错角证明了三角形内角和定理，之后的欧几里得在《几何原本》中通过一组同位角和一组内错角，同样证明了该定理。如图6，在三角形ABC 中，延长BC 至点D，过点C 作AB 的平行线CE，∠BAC=∠ACE （两直线平行，内错角相等）, ∠ABC=∠ECD（两直线平 行，同 位 角 相等），因 为∠ACB ＋∠ACE ＋∠ECD=180°（平角的意义），所以∠ACB＋∠BAC＋∠ABC=180°（等量代换），即三角形内角和等于180°。《几何原本》 中知识的条理化和严密化使它在以后的两千多年里一直是数学史上流传最广的著作之一，堪称西方数学的“圣经”。

以上两种证明方法都采用了平行线的性质，这也是现在中学教材中普遍使用的方法。

图6 欧几里得的证明

2.普罗克拉斯的方法。

古希腊评注家普罗克拉斯（Proclus，410—485年）试图避开毕达哥拉斯和欧几里得用平行线证明三角形内角和定理的方法，他用这样的方法：如图7，设AD 和BE 是AB 的两条垂线段，AD和BE 分别绕点A 和B 旋转，使得端点D 和E 重合于点C，得到三角形ABC，原来的两个直角DAB和EBA 所减小的部分相加，正好等于顶角C。因此，三角形ABC 的三个内角之和仍等于原来两直角。

图7 普罗克拉斯方案

普罗克拉斯的证明是不是绕开了平行线呢？其实并没有，他的方法也可以这样表达：如图8，过三角形ABC 的三个顶点A、B、C 分别作底边BC 的 垂 线 AD、BE 和 CF，∠BAD = ∠EBA,∠CAD=∠ACF（两直线平行，内错角相等），所以∠BAC=∠EBA＋∠ACF, 所以∠BAC＋∠ABC＋∠ACB=∠EBA＋∠ABC＋∠ACF＋∠ACB=∠EBC＋∠FCB=180°。这种方法并不局限于垂线，如图9，在BC 上任取一点D，连接AD，分别过点B、C 作AD 的平行线BE 和CF，三角形内角和转化为一对同旁内角之和。所以普罗克拉斯的方法本质上仍用了平行线的性质。

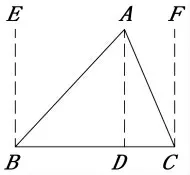
图8 普罗克拉斯方案

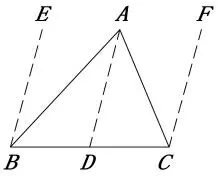
图9 普罗克拉斯方案的一般情况

3.克莱罗的方法。

如果说古人的证明宛若天降，那么18 世纪法国数学家克莱罗（A.C.Clairaut,1713—1765年）为添加平行线提供了一种自然的思考过程，正如他在其《几何原理》一书的前言中所说，他要用定理的最初发现者的方法来引入几何定理。

如图10，设三角形ABC 的顶点C 沿AC 运动到C′、C″,等等。在这个过程中，∠A 保持不变，而∠C 越来越小，∠B 越来越大。猜想：∠C 减少的部分与∠B 增大的部分相等，也就是∠C 与∠B 之和保持不变。由此可以猜测：任何一个三角形的三个内角之和是恒定不变的，当点C 运动到无限远时，BC 与AC 平行，三角形ABC 的三个内角则又变成了两个同旁内角，其和为180°。

图10 克莱罗的方案

4．提波特的方法。

许多数学家在证明三角形内角和定理时，都试图绕开平行线性质，寻求自己独一无二的方法。1809年，德国数学家提波特（Thibaut，1775—1832年）就利用旋转的方法证明了这一定理：如图11，将三角形ABC 中AB 所在的直线xy 绕点A 沿逆时针方向旋转角度A，到AC 所在直线x′y′； 将直线x′y′绕点C 沿逆时针方向旋转角度C，到BC 所在直线x″y″；最后直线x″y″绕点B 沿逆时针方向旋转角度B，到AB 所在直线x″′y″′，从xy 到y″′x″′一共旋转了180°。 在实际教学中，也可以用铅笔的旋转和笔尖方向的改变来再现这种办法（如图12）。而如果考虑顺时针方向旋转，就可证明三角形外角和定理。

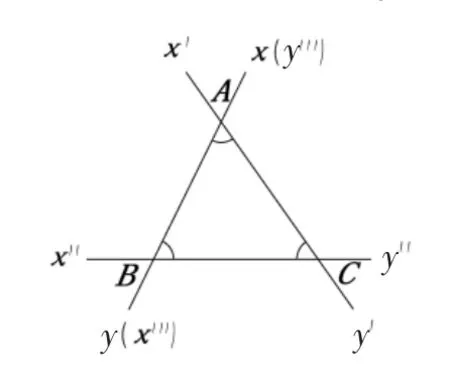
图11 提波特的方案

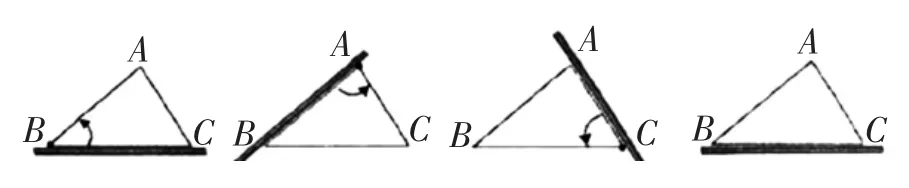
图12 铅笔旋转再现提波特的方案

三中国与三角形内角和定理

三角形内角和定理已有两千多年的历史，与西方数学家热衷于证明此定理相比，中国古算中竟然没有“三角形内角和等于180°”这条定理，也没有其他类似定理。对此，数学家陈省身先生说：“在中国几何中我无法找到类似三角形内角和等于180°的推论，这是中国数学中没有的结果。因此，鉴于国外数学的经验和有机会看中国数学的书，我觉得中国数学都偏应用，讲得过分一点，甚至可以说中国数学没有纯粹数学，都是应用数学。”这个定理没有什么实际应用，因而我们的祖先把它忽略了。

四历史给予的启示

著名数学教育家M.克莱因说，历史是教学的指南。泰勒斯从等边三角形到等腰三角形，再到不等边三角形探索三角形内角和定理的自然发现顺序，也可以成为小学生研究三角形内角和的思考顺序，这也正是数学学习从特殊到一般的归纳推理过程。而更为深远的是，历史上数学家们对于定理证明的孜孜不倦，这种追求体现的正是数学学科最为本质的东西——数学的理性靠合乎逻辑的思考来保证！因而，数学学习可以起于观察、操作、猜测、直觉等，却不能亦终于此。 学生发现了三角形的内角和是180°，在此基础上要进一步引导学生用他们力所能及的办法说明这个发现是可靠的。教学至此，才算触及了数学的灵魂。帕斯卡的折叠法、剪拼法，泰勒斯的拼图法，提波特的旋转法等都是不错的选择。