An improved model for predicting effective Young’s modulus of the twisted structure under cyclic loading: taking into account the untwisting effect
2018-05-19HexinCuiDonghuaYueXingyiZhangYouheZhou
Hexin Cui , Donghua Yue , Xingyi Zhang ,*, Youhe Zhou
a Department of Mechanics and Engineering Sciences, College of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000,China
b Key Laboratory of Mechanics on Disaster and Environment in Western China attached to the Ministry of Education of China, Lanzhou 730000, China
Many years ago, people in China use the twisted hemp to build suspension bridges and miscellaneous household items,which have been maintained till now. Today, the twist structures have diverse applications, ranging from dragline, electrical cable, cable in conduit conductor (CICC), and intelligent structure, etc. Recently, Haines et al. [1] proposed a new kind of intelligent muscles based on the twist structure. Comparing with the traditional artificial muscles, e.g., electrothermally driven shapememory metal, thermally powered shape-memory polymers,hybrid carbon nanotube (CNT) muscles, and electric-field driven electrostrictive polymers, this new kind of artificial muscles has many merits such as fast, scalable, nonhysteretic, long-life,and inexpensive (see Ref. [1] and references therein). Therefore,this kind of artificial muscle shows wide applications including intelligent robots, prosthetic limbs and actuators. During these applications, the stretch deformation does not be avoided,which often leads to the twist structure rotation with the increase in twist pitch. As a result, the cable stiffness will decrease and its Young’s modulus will vary. On the other hand, this untwisting behavior is often observed during some twist structures fabrication process. The CICC is usually used to construct magnet generating high magnetic field by carrying high current [2,3]. In order to counter the coupling loss, the cable is made of multistage twists, and totally inserted into a jacket to bear electromagnetic force. During this insertion, several tons of tension is used to balance friction between the cable and the jacket, serious stretching and untwisting take place in the cable and cause an increase in twist pitch in the last stage of cabling [4-7], as same as stretch process on common twist structures, the cable’s axial stiffness decreases, and its effective Young’s modulus varies. Generally, the cable’s effective Young’s modulus is one of the key mechanical parameters that related to the engineering design and safety assessment. Zhai and Bird [8] and Li et al. [9]analyzed the spring model which can only calculate the deformations of bending and distortion on the twisted strands when axial stretched, and provided a lower predication of the effective Young’s modulus. For evaluating the effective Young’s modulus of twist structure without gap, the classic Costello [10] model can be used, in the case of twist structure with gap, a new theory model presented by Yue et al. [11] can be applied, however, All of these models did not consider the untwisting behavior, this implies that the predicted results can cause failure in fitting in with the experimental results. In this paper, an improved theory based on the Costello model is presented to predict the effective Young’s modulus of the twist structure by taking consideration of the untwisting behavior. The calculated results agree well with experimental results.
Figure 1 shows a classical axial tensile force-displacement curve of a used specimen, which is fabricated by twisting three pure Cu strands with different diameters of 0.8, 1.0, 1.2, and 1.5 mm. The experimental method what we conduct is cyclic loading. As shown in this figure, E1represents the nominal Young’s modulus obtained by initial loading phase, E2, E3, E4, and E5are on behalf of the average effective Young’s modulus which are calculated by cyclic process. The corresponding value of each Young’s modulus is the slope of the calculated stress–strain curve at a given cyclic strain, respectively. In general, the nominal Young’s modulus E1is often lower than the effective Young’s modulus because of the gap among the twisted cooper strands and pre-stress during the fabrication process. After several cyclic processes, the gap among the cooper strands will be disappeared, and the pre-stress will be released gradually. Therefore,the values of E2, E3, E4, and E5come into being convergent, as verified by the experimental process. The theoretic model for nominal Young’s modulus E1has been presented by Yue et al.[11]. In this paper, we focus on the theoretic and experimental investigations on the Young’s modulus E2, E3, E4, and E5after cyclic loading.
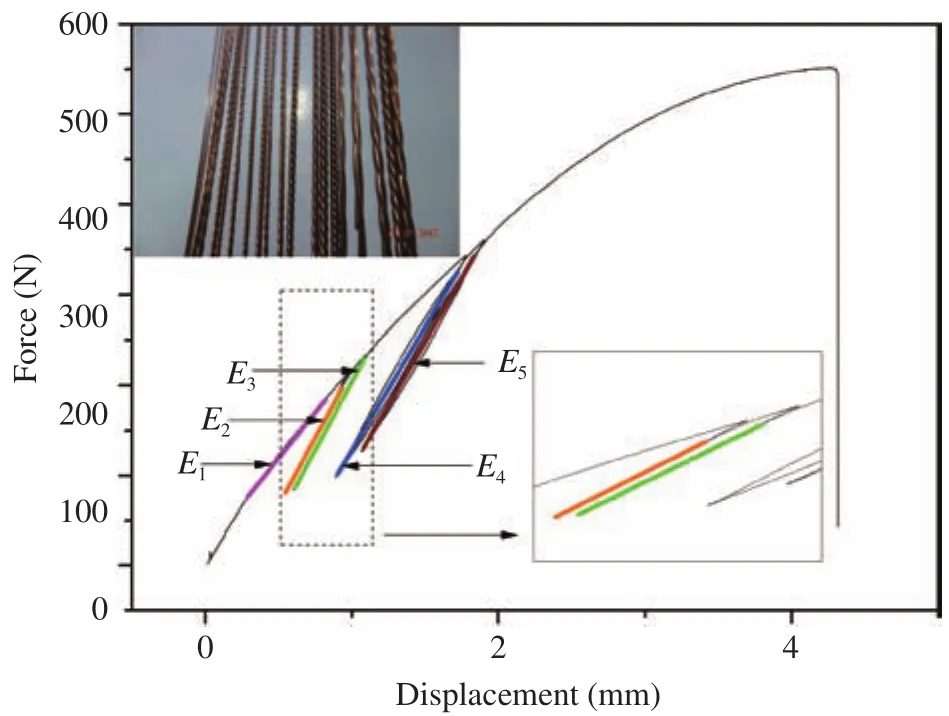
Fig. 1. Axial tensile force-displacement curve (black line) of a used sample. One of insets shows the used samples with different twisted pitch. The other shows the local zoom-in of the cyclic loading process and the definition of the Young’s modulus, where the lines with pink, red, green, blue, and brown color are fitted by linear law.
In the present model, twist structure’s stretching can be divided into two processes: untwisting and elastic deformation, as displayed Fig. 2. In which, two symbolsanddenote the axial strain caused by untwisting and the elastic deformation, respectively. For the untwisting process, if this structure’s elongation and back rotation are raised at the same time, its tension force in axial direction can be regarded as 0. This implied that the twist structure is free to back rotation caused by residual stress, as a result, the triplet’s twisted anglechanges, The untwisting process of the triplet during the tension is schematically showed in Fig. 3(a). One can see that with the triplet stretch, itspitch increases.

Fig. 2. Schematic diagram of the total axial strain of twist structure in the process of axial tension. The total axial strain can be divided into two components: the axial strain caused by untwisting andrelated to elastic deformation.
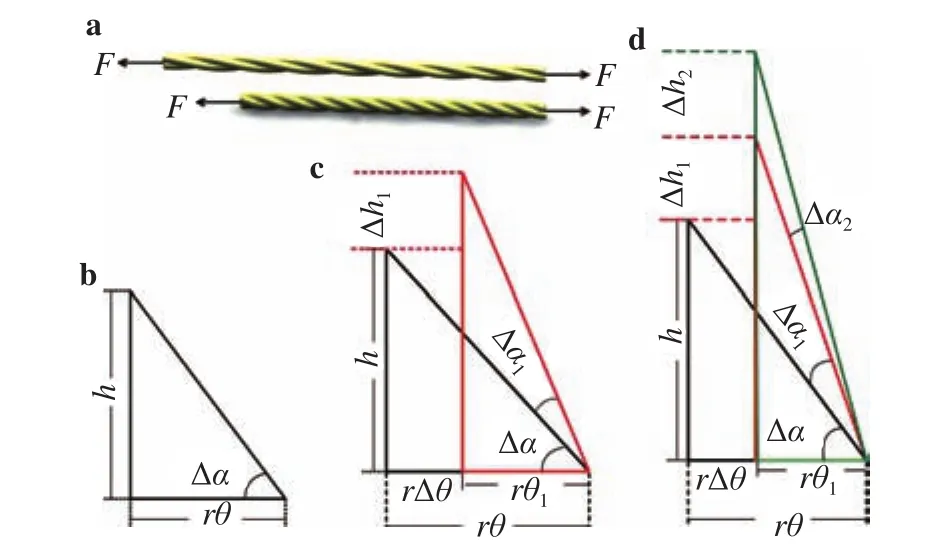
Fig. 3. Schematic diagram of the tension process for the triplet. a Both untwisting and stretching of the triplet with increase in twist pitch when triplet is under the tension, b initial state of triplet. is initial angle, and is initial helix angle. c The state of triplet after untwisting which is denoted by the red triangle. represents untwisting angle, is variation of helix angle produced by untwisting,and is stretch deformation of triplet produced by untwisting. d The state of triplet after untwisting and stretching, showed by the green triangle. is variation of helix angle produced by stretching, is stretch deformation of triplet produced by stretching.
The tension force F of the strands can be expressed as:

where T represents the axial force andis the shear force. E denotes the modulus of the strand. R andrepresent the radius and the initial helix angle, respectively, as displayed in Fig. 3(b).The contact force X between the strands can be written as:
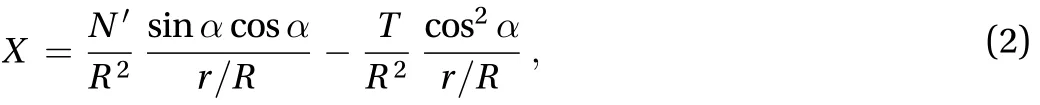
where r represents the radius of the strand. The geometric equations of the strands are listed as following:
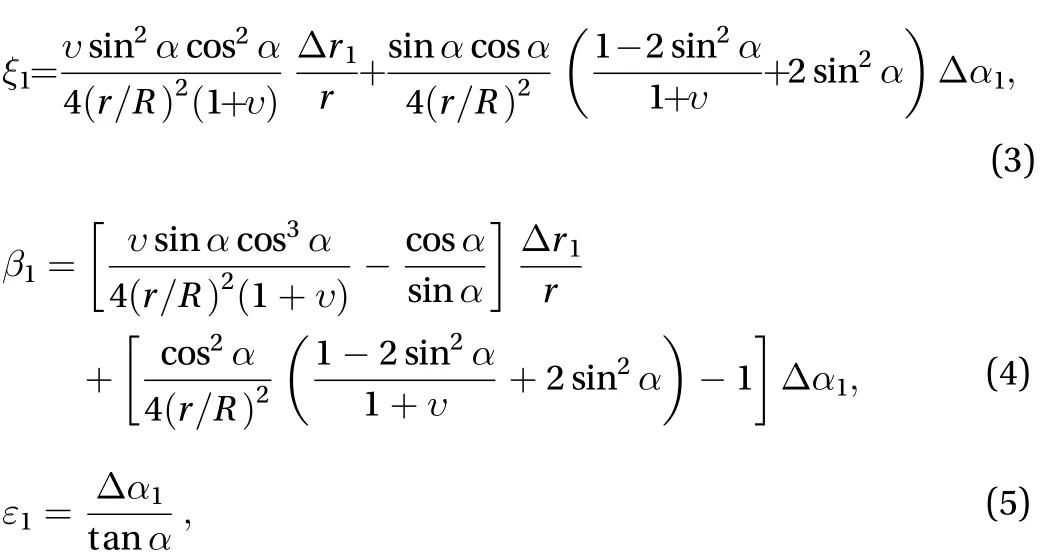
wheredenotes the tensile strain in untwisting process,represents the Poisson's ratio,represents the change of initial helix angle caused by twisting, which is schematically showed in the Fig. 3(c). Using boundary conditions: F = 0 and X = 0,one can obtain from Eqs. (1) and (2) as:

Combining Eqs. (3)–(6), one can deduce the relationship between the axial strainand the untwisting angle:

We now turn to calculate the axial straincaused by the elastic deformation. As same as the above analysis process, we define three symbols,, andto represent the untwist angle caused by elastic deformation, the axial strain of the wire,and the change of twisted angle. This geometric relation is displayed in the Fig. 3(d). The axial strainand the untwist anglecan be calculated by the thin-rod model presented by Costello [10]. One can obtain that:
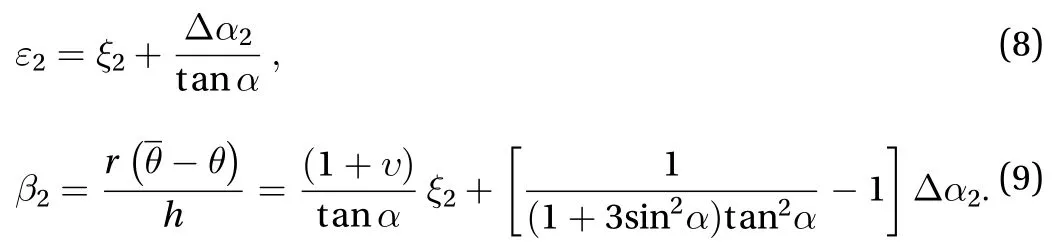
Then, the total straincan be represented as shown below:
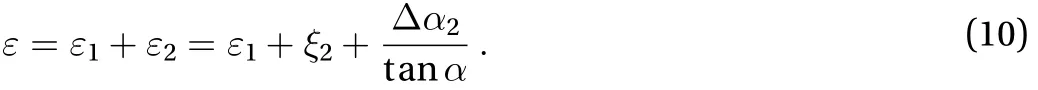
Meanwhile, the tension forcecan also be given by the following expression:

where A represents the cross area of three wires,represents the effective Young’s modulus of the triplet.
In order to verify the suitability of the theoretical model for the strands, four kinds of strands were tested by a universal testing machine. The strands are fabricated by three cooper wires with the same diameters of 0.8, 1.0, 1.2, and 1.5 mm, but with different helical angles. Each sample was tested for four times in the way of cyclic loading. The tensile stiffness of the samples are recorded as E2, E3, E4, and E5respectively. All kinds of specimens have at least three parallel specimens. Then, the untwist angle of each samples are calculated based on the stress-strain data. The relationship between untwist deformation and the helical angle of each kinds of samples are shown in Fig. 4.
According to Fig. 4, it can be seen that the untwist angle is linear with the helical angle of the strand, and increases with the helical angle. A fitting formula was proposed and expressed as

whererepresents the initial helical angel,represents the untwist angle, d represents the diameter of strand, and B is a fitting parameter. There have uniform coefficients of B=7.16344E-3and d0= 0.8 mm, which are suitable for all kinds of the samples. So we can use this fitting formula to describe the linear relationship between the axial strainand the helical angleaccurately. Substituting the untwist angleinto Eq. (7), we can get the corresponding axial strain. Then,the effective modulus of the strand can be obtained by Eq. (11).
Figure 5 displays the comparison between the experimental results and the calculations, In which, the discrete points shows the experimental results of several samples with different initial twist angles, the black line shows the calculated results by using the classical Costello model, and the red line displays the theoretical results by the present model. It is found that the effective Young’s modulus decreases as the helical angle decreases for all diameters of the strands. There exists a significant deviation between the experimental results and theoretic results with the Costello model. One can also find that the modified model agrees very well with the experimental results, which proves the feasibility of this new model.
In summary, we present an improved model based on the classical Costello’s theory to predict the effective Young’s modulus of the twist structure under cyclic loading, which is twisted by three copper lines with same diameter. The untwisting effect is taken into account in the present model. The new model applies to predict the Young’s modules of stretching twisted structures.Series of experiments were carried out to verify the present model. In comparison with the classical Costello’s model, the present model takes good agreements with the experimental results qualitatively and quantitatively.
Acknowledgements
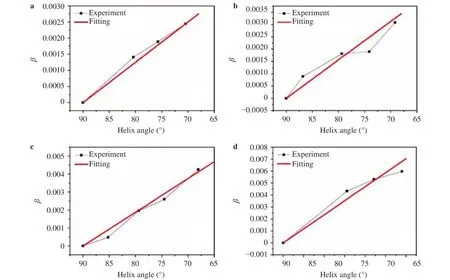
Fig. 4. Untwist angle of the samples in the step of untwisting. a-d represent the samples with the same wire diameters of 0.8, 1.0, 1.2, and 1.5 mm, respectively. The discrete point with black square in the figures are the experimental results, and the lines with red colors are the linear fitting.
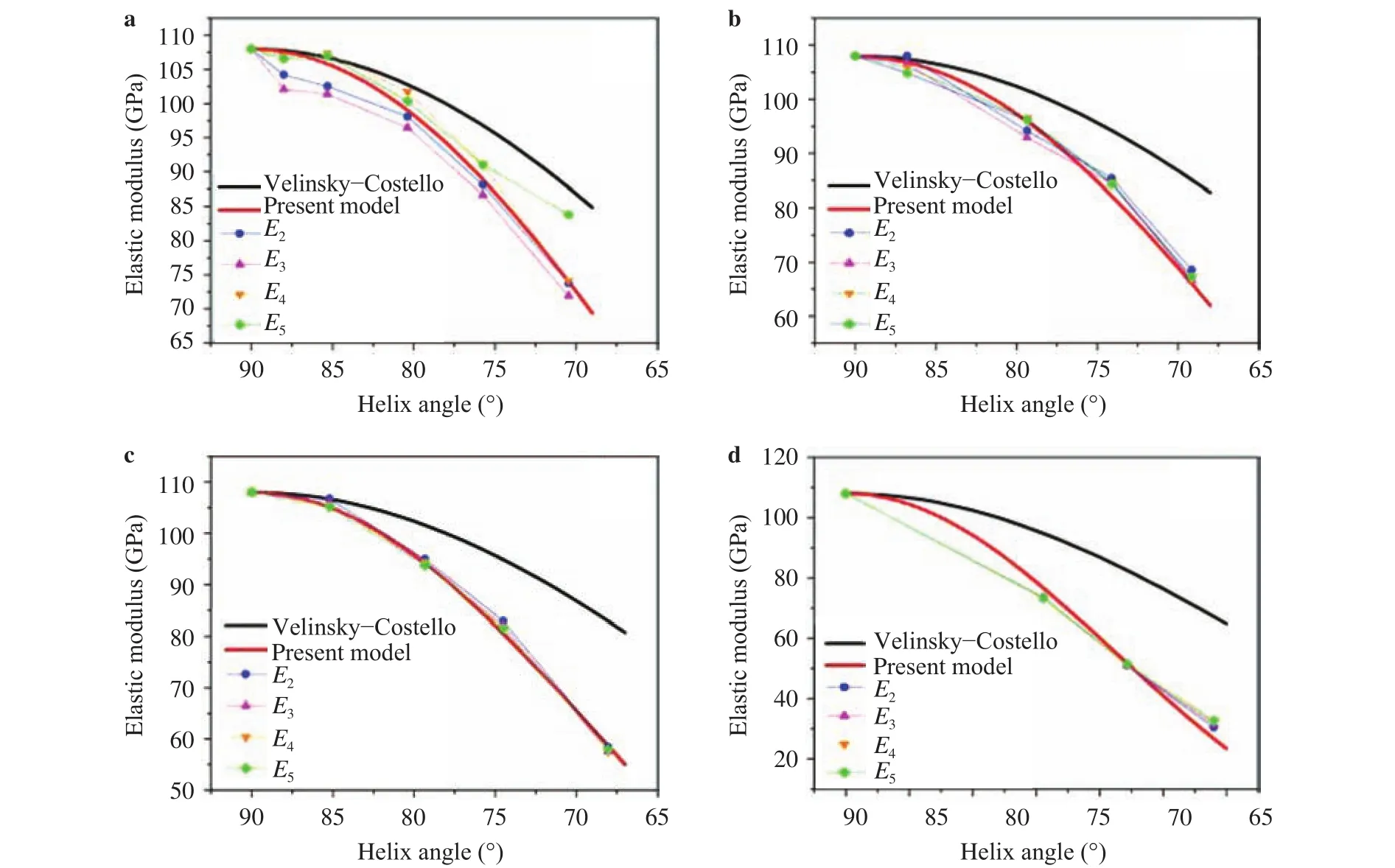
Fig. 5. Comparison between experimental results (points), modified model we present (red line), and Costello model (black line).
This work is supported by the National Natural Science Foundation of China (11622217), the National Key Project of Sci-entific Instrument and Equipment Development (11327802), the National Program for Special Support of Top-Notch Young Professionals. This work is also supported by the Fundamental Research Funds for the Central Universities (lzujbky-2017-ot18,lzujbky-2017-k18).
References
[1]C.S. Haines, M.D. Lima, N. Li, et al., Artificial muscles from fishing line and sewing thread, Science 343 (2014) 868–872.
[2]N. Mitchell, A. Devred, P. Libeyre, et al., The ITER magnets:design and construction status, IEEE Transactions on Applied Superconductivity 22 (2012) 4200809.
[3]A. Vostner, I. Pong, D. Bessette, et al., Benchmarking of mechanical test facilities related to ITER CICC steel jackets, IEEE Transactions on Applied Superconductivity 23 (2013) 9500705.
[4]J.G. Qin, Y. Wu, G. Liao, et al., Cable rotation and twist pitch variation for ITER TF conductor in China, IEEE Transactions on Applied Superconductivity 25 (2015) 1–4.
[5]D.S. Kaverin, V.V. Zubko, K.A. Shutov, et al., VNIIKP RF TF cable untwisting and elongation under tensile force, IEEE Transactions on Applied Superconductivity 24 (2014) 1–4.
[6]Y. Takahashi, Y. Nabara, Y. Nunoya, et al., Cable twist pitch variation in Nb3Sn conductors for ITER toroidal field coils in Japan, IEEE Transactions on Applied Superconductivity 23 (2013)4801504.
[7]T. Suwa, Y. Nabara, Y. Takahashi, et al., Cable behavior during manufacture of a 900-m scale CICC, IEEE Transactions on Applied Superconductivity 26 (2016) 1–5.
[8]Y. Zhai, M.D. Bird, Florida electro-mchanical cable model of Nb3Sn CICCs for high-field magnet design, Superconductor Science and Technology 21 (2008) 115010.
[9]Y. Li, T. Yang, Y. Zhou, et al., Spring model for mechanical–electrical properties of CICC in cryogenic–electromagnetic environments, Cryogenics 62 (2014) 14–30.
[10]G.A. Costello, Theory of Wire Rope, Springer Science & Business Media, 1997.
[11]D. Yue, X. Zhang, J. Zhou, et al., Effective Young’s modulus of the artificial muscle twisted by fishing lines: Analysis and experiment, AIP Advances 5 (2015) 097113.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Graphical Abstract
- Sound absorption characteristic of micro-helix metamaterial by 3D printing
- An analysis of dynamic stability of an elastic column
- Local buckling of thin plate on tensionless elastic foundations under interactive uniaxial compression and shear
- Quantitative characterization of deformation and damage process by digital volume correlation: A review
- Forced vibration analysis of nano-composite rotating pressurized microbeam reinforced by CNTs based on MCST with temperature-variable material properties
