Local buckling of thin plate on tensionless elastic foundations under interactive uniaxial compression and shear

Jianghui Dong, Xing Ma*, Yan Zhuge, Julie E. Mills

School of Natural and Built Environments, University of South Australia, Adelaide, SA 5095, Australia

Plate elements are one of the main components in loadbearing structures and have wide engineering applications in the mechanical, marine, aeronautical, and civil industrial fields.Local buckling of plate elements often occurs when the structures are subjected to compressive and/or shear loadings. The buckling load is one of the governing criteria in steel and composite structural design.

For steel only structures, a plate element is able to buckle laterally both positively and negatively, which is called “bilateral buckling”. The bilateral buckling phenomenon of an isotropic plate under combined in-plane shear and uniaxial compression is well understood. The interaction between ultimate compression and shear has been derived as [1, 2]andwhere σx, τxy, σxcr, and τxycrare the maximum compressive stress during buckling, the maximum shear stress during buckling, the critical stress under pure compressive load alone, and the critical stress under pure uniform shear load alone, respectively.

However, for skin buckling behaviour in composite structures, the support from core materials has to be taken into account. An effective method is to simulate the core material as foundation using a rigid foundation model, either a one-parameter elastic model (like Winkler foundation [3]) or a two-parameter elastic model (like Pasternak foundation [4]). The skin buckling phenomenon is a kind of contact buckling problem,which has been extensively studied, especially for plates under pure compression or pure shearing loads, e.g. the local buckling analysis of plate under compression plate [5-9], local buckling analysis of plate under in-plane shear loads [10-12], and post-buckling analysis [13-15]. For thin-plates under combined loads,current research is focused on skins in unilateral contact with rigid materials. For example, local buckling behaviour of a finite plate with rigid medium under combined loads of bending,compression and shear [16-18] have been investigated.However, the previous combination buckling studies were focused on the rigid foundation, and the elastic tensionless foundation (between the rigid tensionless foundation and without foundation) was not taken into account to address the influence of elastic tensionless foundation on the contact buckling coefficient under combined shear and compression.

The current study addresses the foundation deformation effect on contact buckling behaviour under combined loads. An infinitely long, thin isotropic plate under interactive in-plane shear and uniaxial compressive loads, constrained on a tensionless Winkler foundation is investigated. Both clamped and simply supported edge conditions are considered. The fitted formula of the thin plate is obtained based on the analytical solution. In addition, the analytical results are compared with finite element (FE) simulation using ABAQUS.

A long plate under combined uniform in-plane shear and uniform longitudinal uniaxial compressive loads is illustrated in Fig. 1. The buckling half waves consist of inward half waves and outward half waves. If the foundation is considered, two kinds of zones occur between the plate and foundation, i.e. contact zones(inward half waves) and non-contact zones (outward half waves). For easy mathematical expression, two local Cartesian coordinate systemsandwere introduced in this study.

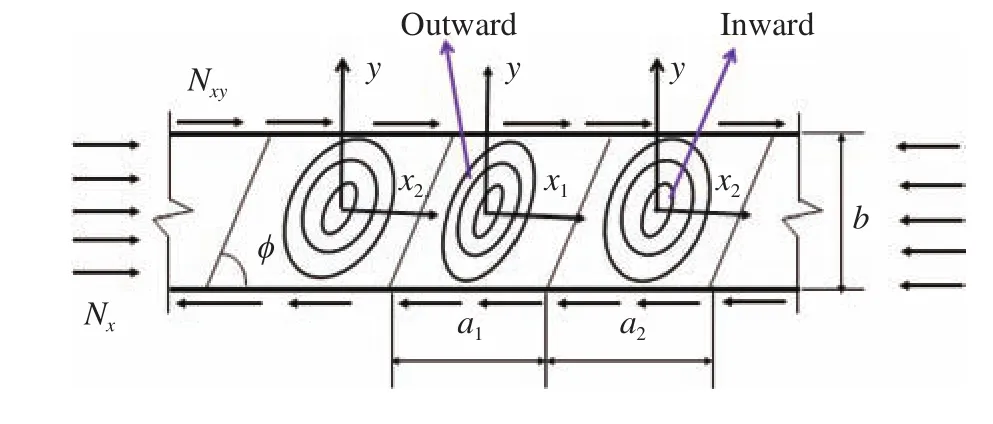
Fig. 1. Geometry of a long plate under combined loadings.

For the local buckling of infinite length thin plates constrained on an elastic foundation under combined uniform longitudinal uniaxial compressive and uniform in-plane shear loads, the governing equation may be written as follows

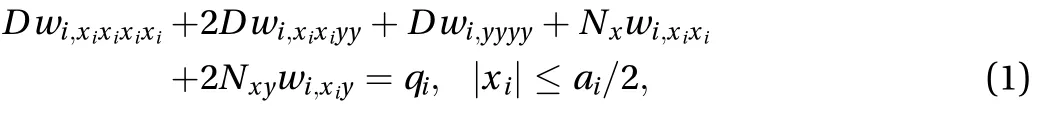
where D, Nx, and Nxyare the plate flexural stiffness, longitudinal uniaxial compressive, and shear force, respectively, which can be expressed as:

where Es, νs, t, σx, and τxyare Young’s modulus, Poisson’s ratio,plate thickness, longitudinal uniaxial compressive stress, and shear stress, respectively.

Assuming the following equations

Eq. (1) may be rewritten as

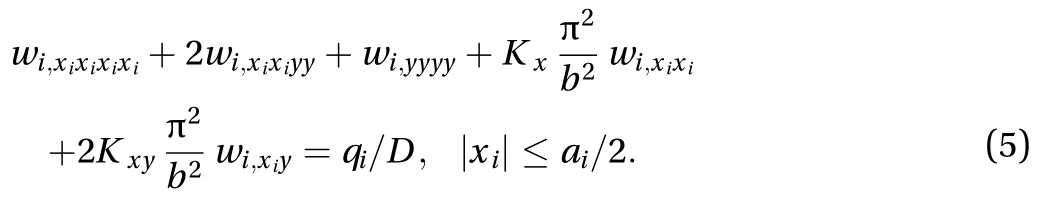
Assumingand the foundation is a Winkler foundation, Eq. (3) can be written as

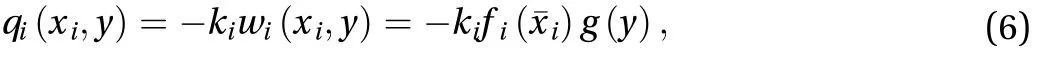
where g and fi(i = 1, 2) are the lateral direction (y-axis) and the longitudinal direction (x-axis) buckling mode function,respectively; kiis the factor of stiffness and k is non-zero and zero for contact areas and for non-contact areas, respectively.

In Eq. (6), according to Fig. 1,can be expressed as

where ϕ is the skewed angle and shown in Fig. 1. Therefore, wimay be presented as a function of c.

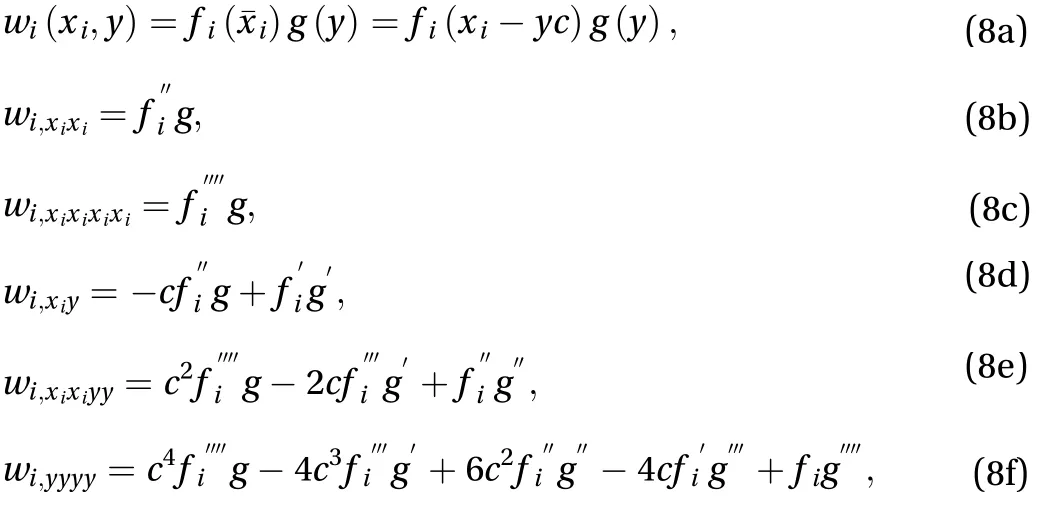
where the superscript " ' " indicates the differentiation about x or y.

Substituting Eq. (8) into Eq. (5), Eq. (5) can be rewritten as Two boundary conditions (i.e. clamped plate and simply supported plate) were considered. The lateral buckling mode function g (y) can be assumed as [19, 20]

According to the different boundary conditions, Eq. (9) may be rewritten

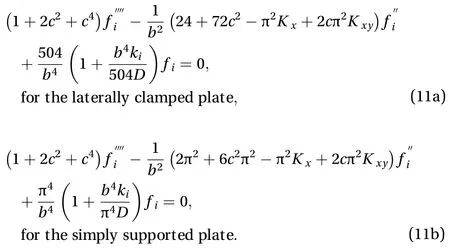
Assuming, we obtain

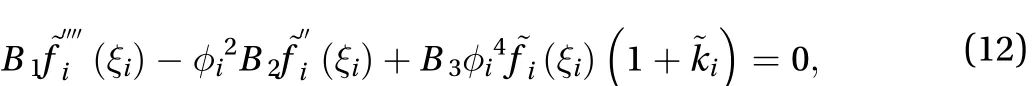
wherefor a clamped plate;for a simply supported plate.

The local buckling coefficient of a thin plate on a tensionless elastic foundation and subjected to combined uniaxial compression and in-plane shear can be obtained (Fig. 2) by solving Eq. (12), and the analytical solution can be expressed by the numerically fitted formula

where the values of p1and p2can be obtained directly from Table 1 based on the different values of lgkr.

For the limiting case of a plate with a very soft foundation,e.g., kr= 0.001, the contact buckling coefficients are close to those from an unstrained plate without foundation [21], and the interactive formula can be represented byfrom Refs. [1, 2, 22]. Figure 2 demonstrates that the proposed solutions agreed well with Nemeth [21] for both clamped and simply supported edges. The contact buckling coefficients of long thin plate without foundation and with rigid tensionless foundation under shear and uniaxial compression are summarized in Table 2.The contact buckling coefficient differences between without foundation and with rigid tensionless foundation are listed in Table 2 as well. The increase percentage decreases with the reducing of the component of compression in ratio of loads(Nx/Nxy).

Fig. 2. Buckling coefficient interaction curves of thin plate resting on a tensionless foundation under combined longitudinal uniaxial compressive and in-plane shear loading, a clamped and b simply supported edges.

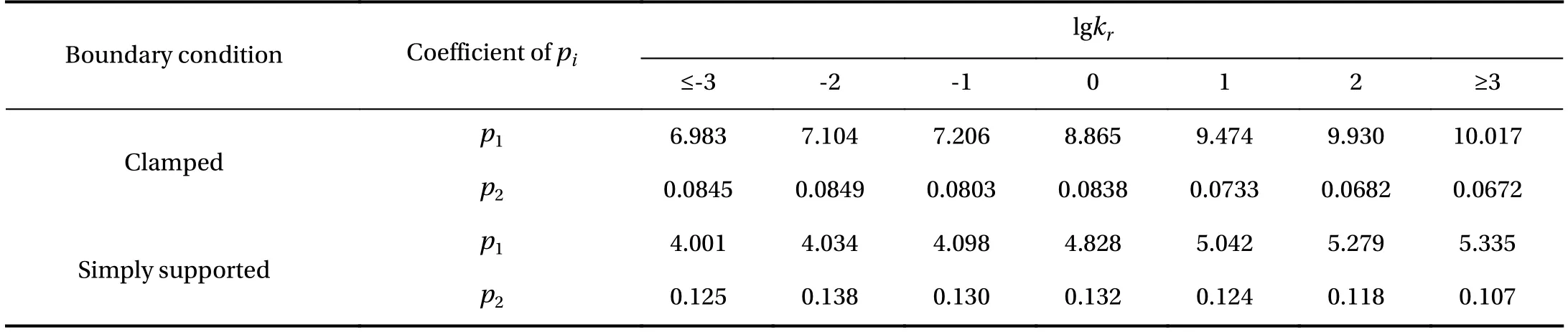
Table 1 Values of pi.

The commercial software ABAQUS was used to perform the contact buckling analysis of a steel plate. In this study, the material properties for the steel sheet are: Es= 205 GPa, vs= 0.3. The dimensions of the steel plate were t = 1 mm (plate thickness), l =2000 mm (plate length), b = 200 mm (plate width). In the FE analysis, the plate was represented as S8R elements.

To determine the appropriate mesh size of the FE model, a convergence study was implemented. A thin steel unrestrained plate with clamped edges under uniaxial compression was analysed. Seven mesh sizes were used in the convergence study(Table 3). In all FE simulations, each element has equal edges, in other words each element is square. The FE analysis results of compressive stress and buckling coefficient are presented in Table 3. In addition, according to previous discussion, the exact solution of the buckling coefficient for the unrestrained plate with clamped edges under uniaxial compression is.Thus, the relative percentage discrepancy between the FE and an alytical solutions can be calculated bywhereis the FE result. The percentage discrepancybetween the FE and analytical results is illustrated in Fig. 3. From Table 3 and Fig. 3, it can be found that 10 mm × 10 mm mesh size can provide sufficiently accurate results.

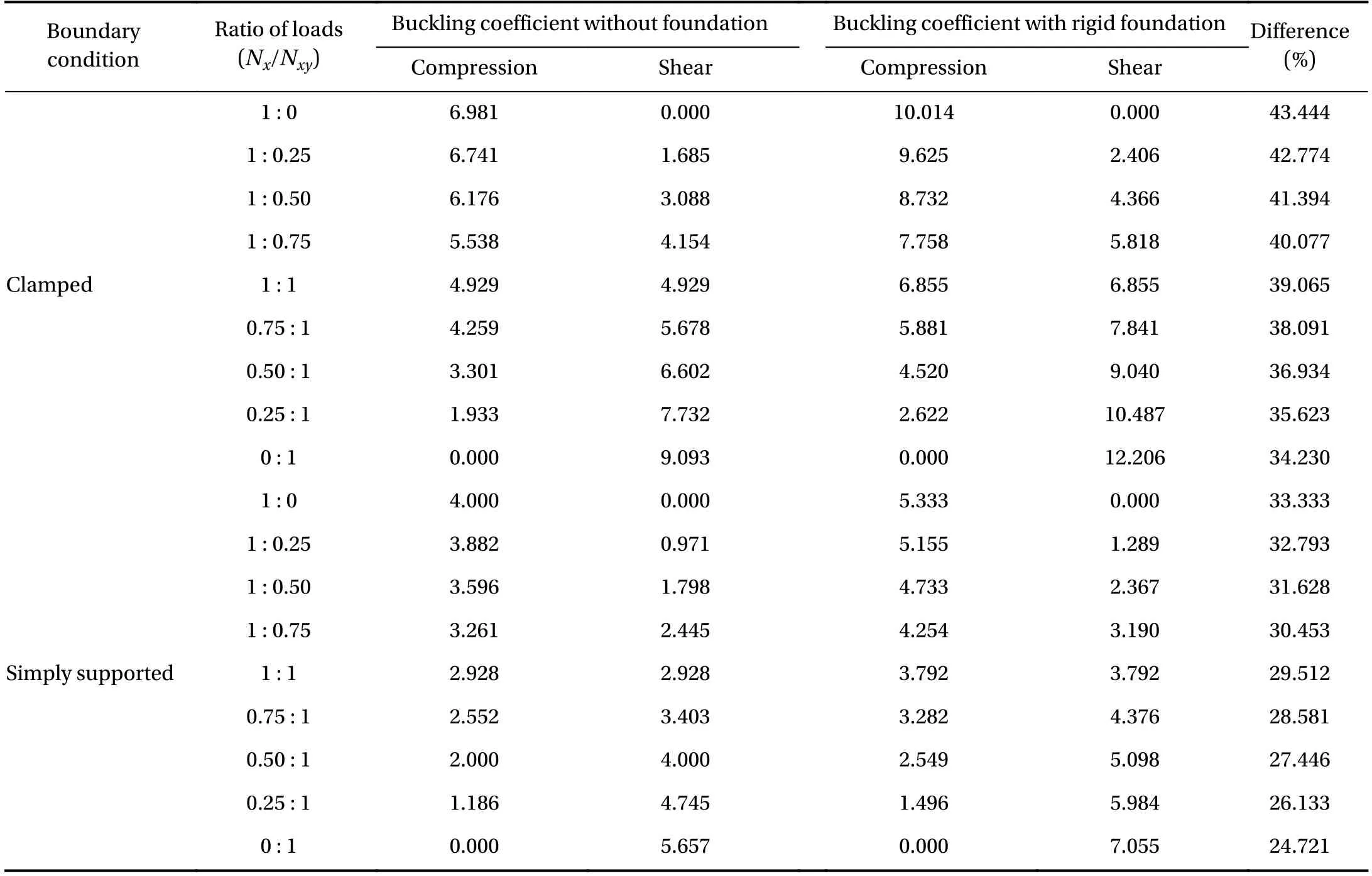
Table 2 Contact buckling coefficients without foundation and with rigid tensionless foundation under shear and uniaxial compression.

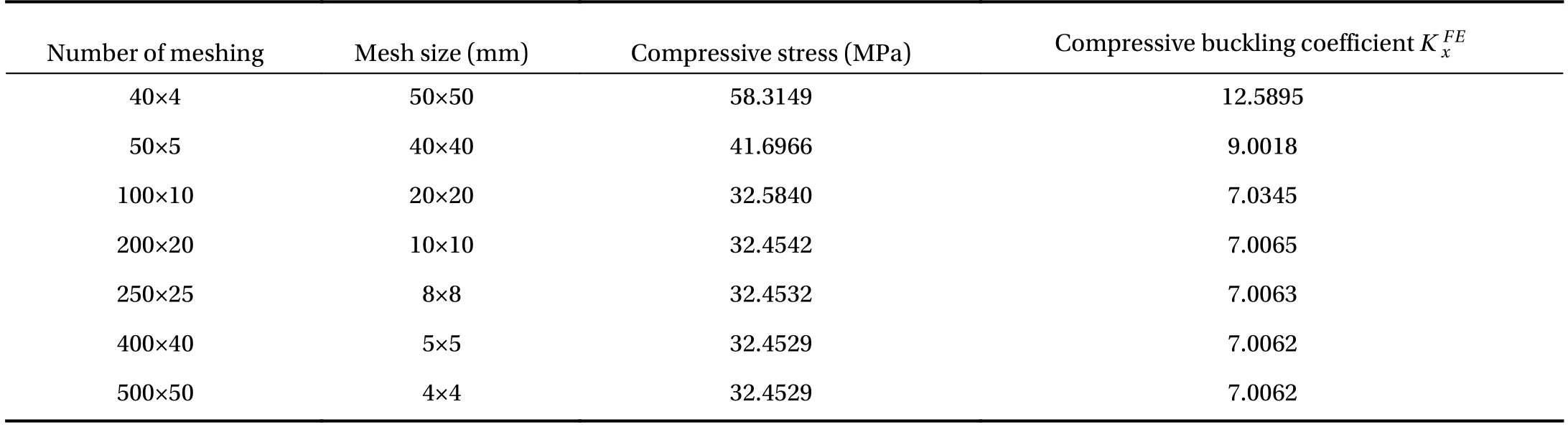
Table 3 Convergence of buckling for thin steel unstrained plate with clamped under longitudinal uniaxial compression.

Consider a long steel skin sheet resting on an elastic tensionless concrete (Fig. 4). The foundation was represented as a tensionless Winkler foundations (Fig. 4(b), (c)).

Based on Eqs. (4) and (10), the analytical solution of buckling stress for the thin steel unrestrained plate was obtained for different ratios of compressive buckling stress and shear buckling stress (Table 4). Furthermore, a comparison between the analytical solution and the FE result was performed (Table 4). As shown in Table 4, the maximum discrepancy is less than 5%,thus indicating very good agreement.

The buckling interaction curves of a thin steel plate with the different foundation stiffness parameters for both clamped and simply supported edges are presented in Fig. 5. Figure 5 shows that the buckling stresses increase with increasing foundation stiffness for the same stress ratio of in-plane shear and compres-sion. In Fig. 5, the results from numerical fitted and FEM are presented along with the analytical solution. Good agreement was obtained between each method.

Table 4 Buckling stress of thin steel plate under foundation stiffness factor kr = 0 (unrestrained plate).

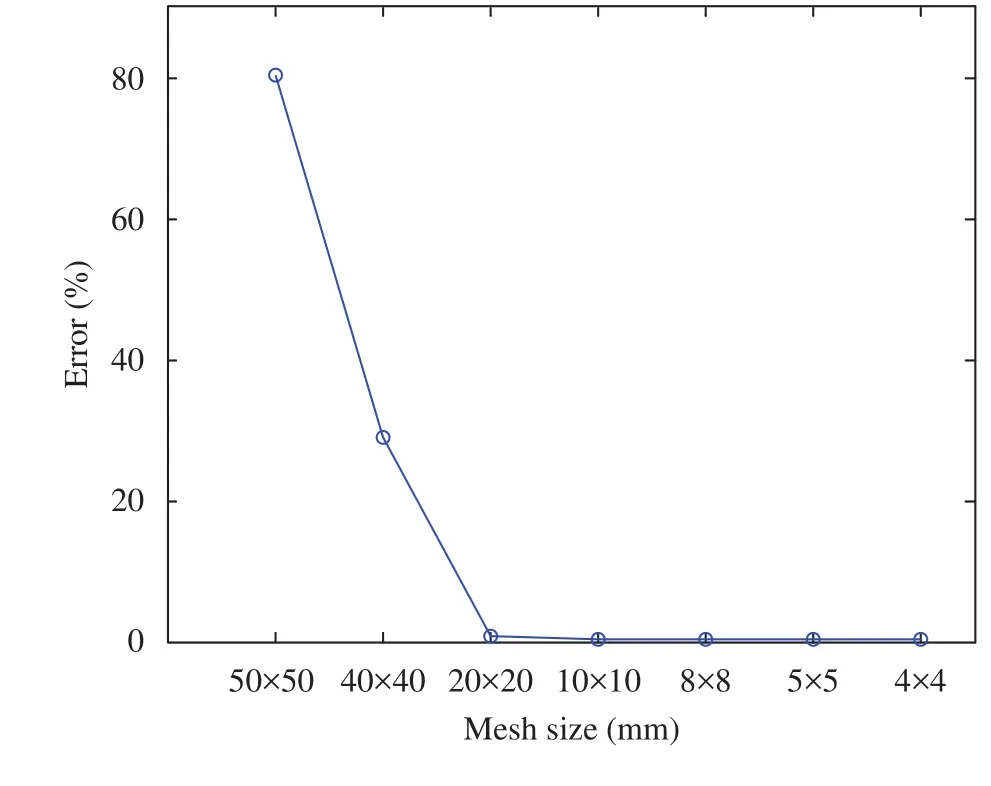
Fig. 3. Convergence curve.

Fig. 4. Schematic diagram of steel skin sheet on the concrete. a Steel skin sheet; b steel sheet on elastic foundation; c Winkler springs model.

The buckling modes of a thin steel plate on an elastic foundation from FEM under pure longitudinal uniaxial compressive,combined loads and pure in-plane shear are given in Figs. 6-8,respectively. As shown in Figs. 6-8, when the foundation stiffness parameter is kr= 0.001, the lengths for both inward and outward half waves are virtually the same. While for cases with foundation stiffness parameter kr= 1000, the length of inward half waves equals zero (there are no inward half waves at all) and only outward half waves are left. This phenomenon is consistent with the previous studies. The numbers of the half waves under combination tends to decrease with reduction of compression and increase of shear.

Consider a thin fully clamped steel plate resting on a tensionless foundation subjected to a combination of in-plane shear and longitudinal axial compressive loads. The parameters of the foundation are: l = 2000 mm, d = 100 mm, b = 200 mm, where l,d, and b are length, height, and width of the foundation, respectively (Fig. 9). Two kinds of foundation are considered, i.e. concrete (vf= 0.2 and Ef= 32 × 103 MPa) and soft filler material (assume the elastic modulus is 3.8 MPa and vf= 0.08), and vfand Efare Poisson’s ratio and elastic modulus of the foundation, respectively. The effective foundation stiffness krmay be calculated bycan be determined from Ref.[23], thus krmay be calculated. The compressive stress and shearstress can be calculated byandrespectively, and Kxand Kscan be obtained by using Eq. (10) or Eq. (11). The detailed general analysis procedure for the clamped plate is shown below and the result is shown in Fig. 10.

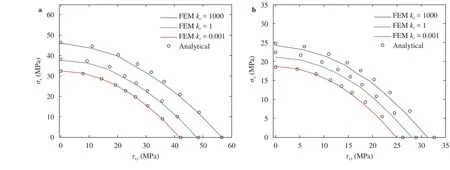
Fig. 5. Buckling stress interaction curves of steel skin sheet on the tensionless foundation under combined longitudinal uniaxial compressive and in-plane shear loading, a clamped and b simply supported.

Fig. 6. Buckling model of FE simulation of a steel skin sheet resting on an elastic foundation under pure axial compression. a kr = 0.001 with clamped edges; b kr = 0.001 with simply supported edges; c kr = 1 with clamped edges; d kr = 1 with simply supported edges; e kr = 1000 with clamped edges; f kr = 1000 with simply supported edges.

Fig. 7. Buckling model of FE simulation of a steel skin sheet resting on an elastic foundation under pure in-plane shear loading. a kr = 0.001 with clamped edges; b kr = 0.001 with simply supported edges; c kr = 1 with clamped edges; d kr = 1 with simply supported edges; e kr = 1000 with clamped edges; f kr = 1000 with simply supported edges.

Fig. 8. Buckling model of FE simulation of a steel skin sheet resting on an elastic foundation under longitudinal axial compressive and in-plane shear loading ( ). a kr = 0.001 with clamped edges; b kr = 0.001 with simply supported edges; c kr = 1 with clamped edges; d kr = 1 with simply supported edges; e kr = 1000 with clamped edges; f kr = 1000 with simply supported edges.

(1) Determine dimensional parameters and material properties (Ef, νf, Es, νs, d, b, l, and t).

(2) Determinevalue based on d/b and vf[23].

(3) Calculate krvalue using[23].

(4) Determine the buckling coefficient Kxand Kxy.

(6) Plot the buckling interaction curve for the plate under compressive stress and shear stress based on the values of σxand τxy.

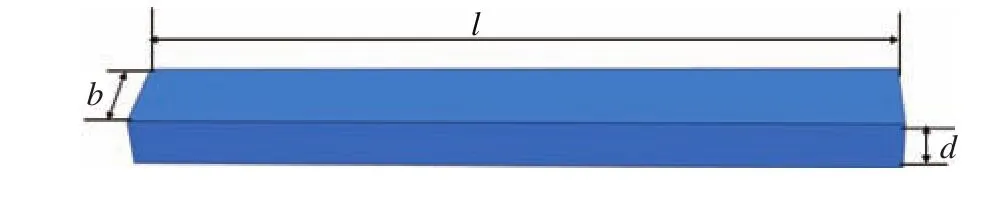
Fig. 9. Geometry of the foundation.

In this example, an FE analysis was carried out to further validate the proposed method. The interaction curves of the thin steel sheet are plotted for both soft filler material and concrete foundations (Fig. 10). From Fig. 10, it is clearly observed that the stresses from the proposed method and FEM agree very well.Additionally, the buckling modes from FEM as presented in Fig. 11 are consistent with Figs. 6-8. For the case with soft filler material, the buckling modes are close to the foundation stiffness parameters between kr= 1 and kr= 10 in Figs. 6-8, and for concrete foundation, the buckling modes are close to the foundation stiffness kr= 1000 in Figs. 6-8. It can be concluded that the current method is reasonable based on the FE analysis.

Fig. 10. Buckling stress interaction curve of a steel plate resting on the foundation.

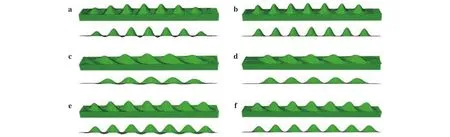
Fig. 11. Buckling shape of the steel sheet on foundation. a Soft filler material under pure longitudinal compression; b concrete under pure longitudinal compression; c soft filler material under pure shear loading; d concrete under pure shear loading; e soft filler material under combination ( ); f concrete under combination ( ).

The buckling problem of an infinitely long sheet on a tensionless elastic foundation under combined loads (i.e. uniform in-plane shear and uniaxial compressive loads) was analysed using theoretical and numerical methods in this study. Based on the analytical solution, the approximate fitted formula for clamped and simply supported thin plate are obtained for loading cases of uniaxial compression, in-plane pure shear and a combination of compression and shear. The interactive curves for the thin plates under combined loads are presented. The effect of the foundation deformation on the contact buckling behaviour of thin sheets was studied by adjusting the foundation stiffness. The analytical results show that the buckling coefficient increases with the increase of the foundation stiffness. In addition, the contact buckling behaviour changes with different edge conditions. The buckling modes of thin plates with simply supported boundary conditions tend to have lesser half waves than those with clamped boundary conditions. The values of the critical buckling coefficient with clamped edges are larger than those with simply supported edges. The numbers of the half waves under combination loads tend to decrease with reducing compression and increasing shear loads. The solution developed in the current study can be used to analyse the elastic local buckling of composite structures like steel-concrete thinwalled structure under combined loads (uniaxial compression and in-plane shear) in the preliminary design phase.

References

[1]E.Z. Stowell, E.B. Schwartz, Critical stress for an infinitely long flat plate with elastically restrained edges under combined shear and direct stress, [Technical Report], National Aeronautics and Space Admin Langley Research Center, Hampton VA,USA, 1943.

[2]S. Batdorf, M. Stein, Critical combinations of shear and direct stress for simply supported rectangular flat plates. NACA Tech,Note 1223 (2nd edn.), National Advisory Committee for Aeronautics, US Government Printing Office, Washington DC, 1947.

[3]E. Winkler, Die Lehre von der Elasticitaet und Festigkeit,Dominicus, Prague, 1867.

[4]P. Pasternak, On a new method of analysis of an elastic foundation by means of two foundation constants, Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu i Arkhitekture, Moscow,1954.

[5]O. Vaseghi, H.R. Mirdamadi, D. Panahandeh-Shahraki, Nonlinear stability analysis of laminated composite plates on onesided foundation by hierarchical Rayleigh–Ritz and finite elements, International Journal of Non-Linear Mechanics 57(2013) 65–74.

[6]B. Uy, M.A. Bradford, Elastic local buckling of steel plates in composite steel-concrete members, Engineering Structures 18(1996) 193–200.

[7]H. Wright, Buckling of plates in contact with a rigid medium,Structural Engineer 71 (1993) 209–215.

[8]S.T. Smith, M. Bradford, D. Oehlers, Unilateral buckling of elastically restrained rectangular mild steel plates, Computational Mechanics 26 (2000) 317–324.

[9]K.W. Shahwan, A.M. Waas, Elastic buckling of infinitely long specially orthotropic plates on tensionless foundations, Journal of Engineering Materials and Technology 113 (1991) 396–403.

[10]S.T. Smith, M.A. Bradford, D.J. Oehlers, Elastic buckling of unilaterally constrained rectangular plates in pure shear, Engineering Structures 21 (1999) 443–453.

[11]S.T. Smith, M.A. Bradford, D.J. Oehlers, Numerical convergence of simple and orthogonal polynomials for the unilateral plate buckling problem using the Rayleigh-Ritz method, International Journal for Numerical Methods in Engineering 44(1999) 1685–1707.

[12]A. Arabzade, H. Moharami, A. Ayazi, Local elastic buckling coefficients of steel plates in composite steel plate shear walls,Scientia Iranica 18 (2011) 9–15.

[13]H. Chai, Contact buckling and postbuckling of thin rectangular plates, Journal of the Mechanics and Physics of Solids 49 (2001)209–230.

[14]A. de Holanda, P. Gonçalves, Postbuckling analysis of plates resting on a tensionless elastic foundation, Journal of engineering mechanics 129 (2003) 438–448.

[15]H.S. Shen, J.G. Teng, Postbuckling analysis of unilaterally constrained laminated thin plates, Composite Structures 66 (2004)571–578.

[16]S.T. Smith, M.A. Bradford, D.J. Oehlers, Local buckling of sideplated reinforced-concrete beams. I: Theoretical study, Journal of Structural Engineering 125 (1999) 622–634.

[17]S.T. Smith, M.A. Bradford, D.J. Oehlers, Local buckling of sideplated reinforced-concrete beams. II: Experimental study,Journal of Structural Engineering 125 (1999) 635–643.

[18]M.A. Bradford, S.T. Smith, D.J. Oehlers, Semi-compact steel plates with unilateral restraint subjected to bending, compression and shear, Journal of Constructional Steel Research 56(2000) 47–67.

[19]R. Jones, B.J. Milne, Analysis of clamped rectangular orthotropic plates subjected to a uniform lateral load, International Journal of Mechanical Sciences 45 (1976) 309–316.

[20]M. Dalaei, A.D. Kerr, Analysis of clamped rectangular orthotropic plates subjected to a uniform lateral load, International Journal of Mechanical Sciences 37 (1995) 527-535.

[21]M.P. Nemeth, Buckling behavior of long anisotropic plates subjected to combined loads, National Aeronautics and Space Administration, Langley Research Center (1995).

[22]P.M. Weaver, M.P. Nemeth, Improved design formulas for buckling of orthotropic plates under combined loading, AIAA Journal 46 (2008) 2391–2396.

[23]X. Ma, J.W. Butterworth, G.C, Clifton, Practical analysis procedure for compressive local buckling of skin sheets in composite panels, International Journal of Advanced Steel Construction 4(2008) 230–242.